scikit-learnのモジュール内には特徴量選択のクラスがあるのですが,どのような原理で動作して、どういうときに何のクラスを使えばよいかわからなかったので少しまとめてみました。
そもそも特徴量選択とは何か
特徴量選択 (feature selection) とは、データにある特徴量の集合から、部分集合を選択するプロセスのことを指します。1 元の特徴量や生データから新しく特徴量を作り出す行為は特徴抽出 (feature extraction) と呼ばれ、別モノのようです。
特徴量選択は主に、以下の3つのカテゴリに分類できます。
wrapper method
特徴量の部分集合を取り出し、それらを使ってモデルを訓練し、そのモデルで予測をした誤差を評価していき最適な部分集合を決める
部分集合を取り出すときに、以下のfilter methodのfilterを使うこともあるようです。
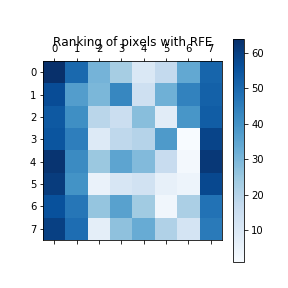
例: RFE (Recursive Feature Elimination) を用いて、Support Vector Classificationモデルで各特徴量の重要度をランキングしたものです。値が小さいほど重要度が高いです。
(元のコード: Recursive feature elimination — scikit-learn 0.19.1 documentationsearch)
from sklearn.svm import SVC
from sklearn.datasets import load_digits
from sklearn.feature_selection import RFE
import matplotlib.pyplot as plt
# Load the digits dataset
digits = load_digits()
X = digits.images.reshape((len(digits.images), -1))
y = digits.target
# Create the RFE object and rank each pixel
svc = SVC(kernel="linear", C=1)
rfe = RFE(estimator=svc, n_features_to_select=1, step=1)
rfe.fit(X, y)
ranking = rfe.ranking_.reshape(digits.images[0].shape)
# Plot pixel ranking
plt.matshow(ranking, cmap=plt.cm.Blues)
plt.colorbar()
plt.title("Ranking of pixels with RFE")
plt.show()
出力:
filter method
特徴量の部分集合を取り出し、その部分集合そのものに対してピアソンの積率相関係数などの指標を用いて評価をし、最適な部分集合を決める
wrapper methodとは違って部分集合の評価にモデルが介入しないため、各モデルに対してtuningされていない汎用的な評価によって重要度を算出します。そのため、wrapper methodによる出力はどのモデルに対しても使用できる特徴量の集合にはなる一方、filter methodに比べて予測性能が劣ることがしばしばあるようです。
また、filter methodは先のwrapper methodの前処理として使われることがあります。
多くのfilter methodのfilterは最も良い部分集合を返すよりも、各特徴量のスコアをランキングした形式で返すことが多いようです。
例: 4つの特徴量のうち、SelectKBestを用いて重要な2つに絞ります。
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
%matplotlib inline
iris = load_iris()
X, y = iris.data, iris.target
selector = SelectKBest(chi2, k=2)
X_new = selector.fit_transform(X, y)
print('original features count: {}, selected features count: {}'.format(X.shape[1], X_new.shape[1]))
print('feature importance: ', selector.scores_)
print('pvalues: ', selector.pvalues_)
出力:
original features count: 4, selected features count: 2
feature importance: [ 10.81782088 3.59449902 116.16984746 67.24482759]
pvalues: [ 4.47651499e-03 1.65754167e-01 5.94344354e-26 2.50017968e-15]
embedded method
Lassoなどの特定のモデルの訓練に組み込んで特徴量を選択する
モデルの中には特徴量選択に使えるものもあります (大体のモデルは使える?)。有名なものとしてLassoがありますが、これは重要度が低い特徴量の係数が0になりやすいように設計された誤差関数を元に訓練をすることで、重要な特徴量のみがモデルの中に残るようになるものです。このようなモデルの訓練をすることで、モデルの訓練と一緒に邪魔な特徴量を排除することができます。
scikit-learnではSelectFromModelの関数を使うことで簡単に実現できます。
例: モデルとしてLassoを指定したSelectFromModel関数を使うことで、13個あった特徴量を7個に減らしています。sfm.get_support()の出力でFalseになっている箇所が削除された部分です (なお、SelectFromModelは係数が0じゃなくても閾値以下の係数の特徴量を削除することができます。)。
import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_boston
from sklearn.feature_selection import SelectFromModel
from sklearn.linear_model import Lasso
%matplotlib inline
boston = load_boston()
X, y = boston['data'], boston['target']
clf = Lasso(alpha=3)
sfm = SelectFromModel(clf)
sfm.fit(X, y)
n_features = sfm.transform(X).shape[1]
print(sfm.get_support())
print('original features count: {}, selected features count: {}'.format(X.shape[1], n_features))
出力:
[False True False False False False True False True True True True
True]
original features count: 13, selected features count: 7
どんなときに特徴量選択を使用するか
特徴量選択をするときは、特徴量の数が多く、サンプル数サイズが少ないときに行うことが多いです (つまり、そのままデータを訓練に使用すると過学習の危険があるとき)。
Wikipedia2では、特徴量選択をする目的として4つ挙げています。
- モデルの訓練にかかる時間を短くする
- 次元の呪いを避ける
- モデルを単純化して解釈しやすくする
- 過学習を避けることで汎化性能を上げる
1, 2はわざわざ特徴量選択をしなくても、PCAで次元削減をしてやれば解決できると思います。
4つ目の過学習を避けることで汎化性能を上げるというのは、データが(母集団の分布を反映するくらい)十分にあれば過学習は起こらないはずです。
なので特徴量選択を行うのは、特徴量の数に対してデータ数が十分でなく、かつPCAなどで次元削減ができない (どの特徴量が重要であるかを説明する必要があるときなど?) ときがよいのではと思っております (違ったらコメントいただければ幸いです)。
scoring function
filter methodに使う指標としての関数を挙げていきます。
以下、単変量特徴量に対する特徴量選択のscoring functionに絞って説明をします。
つまり、以下に挙げる関数は特徴量同士が独立であるという前提がある上で適切に動作するものであることに注意してください (multivariate selectionについては私の知識が足りないため解説できません)。
classificationの際に使うscoring function
分類問題の際に使用するscoring functionについて挙げていきます。
chi2
$\chi^2$統計量をそれぞれの特徴量に対して計算して、scoringをします。
$\chi^2$統計量の計算なので、各特徴量は非負の値でなければならないことに注意してください。
f_classif
univariate_selection - f_classif
ANOVA f-valueを計算します。
中で使われているf_oneway()はそれぞれの特徴量に関する分布の平均が一致していることを帰無仮説として検定を行います。
以下の前提がある状態で検定を行うことに注意してください。
- それぞれの特徴量は独立である
- それぞれの特徴量の母集団の分布は正規分布である
- それぞれの特徴量の母集団の分布の分散はすべて等しい
mutual_info_classif
mutual_info - nutual_info_classif
相互情報量を計算します。non-parametricな手法なので各特徴量の分布は正規分布である必要はなく、非線形な相関関係も検出することができますが、parametricな手法と比べてよりサンプル数サイズを必要とします。
regressionの際に使うscoring function
回帰問題の際に使用するscoring functionについて挙げていきます。
scikit-learn公式のページにも書かれていますが、回帰問題のfeature selectionを行う際にclassification用のscoring functionを使わないようにしましょう。出力されるスコアが意味のない値になるので、選択の基準がわけわからないものになります。
f_regression
univariate_selection - f_regression
各特徴量と目的変数との相関係数を計算して、その値からF scoreを計算し、p-valueを求めます。
p-valueの値が小さい順にソートすることで、特徴量の重要度が分かるという寸法です。
ピアソンの積率相関係数からF scoreを計算する部分の理解が中々できなかったので、ここに計算過程を書いておきます。
標本の$i$番目の目的変数の値を$Y_i$, $i$番目の誤差項を$e_i$, 目的変数の平均値を$\bar Y$とおくと、決定係数$R^2$は以下の式で書けます。
\begin{align*}
R^2 &= 1 - \frac{\sum e_i^2}{\sum(Y_i - \bar Y)^2}\\
&= 1 - \frac{S_e}{S_{yy}}
\end{align*} \tag{1}
上の式で$\sum e_i^2$を$S_{e}$, $\sum(Y_i - \bar Y)^2$を$S_{yy}$とおいています。
また、回帰によって得られたモデルに$\boldsymbol{X}_i$を入力した結果出力される値を$\hat Y_i$とおくと、決定係数は以下のようにも書けます。
\begin{align*}
R^2 &= 1 - \frac{\sum e_i^2}{\sum(Y_i - \bar Y)^2}\\
&= \frac{\sum(Y_i - \bar Y)^2 - \sum e_i^2}{\sum(Y_i - \bar Y)^2}\\
&= \frac{\sum(\hat Y_i - \bar Y)^2}{\sum(Y_i - \bar Y)^2}\\
&= \frac{S_r}{S_{yy}}\\
\end{align*} \tag{2}
($\sum(\hat Y_i - \bar Y)^2$を$S_r$とおいています。つまり、$S_r = S_{yy} + S_e$)
$(2)$でこのように式展開できるのは、$Y_i = \hat Y_i + e_i$という関係があるからです。
$(1)$, $(2)$より、$S_{yy}$を消去すると、
R^2 = 1 - \frac{S_e R^2}{S_r}\\
\therefore \frac{S_r}{S_e} = \frac{R^2}{1 - R^2}
さて、回帰分散$V_r$と残差分散$V_e$を考えると、
V_r = \frac{S_r}{p}
V_e = \frac{S_e}{n - (p + 1)}
ここで、$p$は特徴量の数とします。$V_r$の分母が$p$なのは自由度が特徴量の数$p$だからであり、$V_e$の分母が特徴量の数+1の$p + 1$で引かれているのは、残差の平均値が0である$\sum \hat e_i = 0$という束縛条件と、回帰による変動と残差が直交するという条件$\sum \hat e_i (\hat y_i - \bar y) = 0$があるので、その分自由度が小さくなるからです。
さて、$F = V_r / V_e$という値を考えると、
\begin{align*}
F &= \frac{V_r}{V_e}\\
&= \frac{S_r/p}{S_e/(n-(p+1))}\\
&= \frac{R^2}{1 - R^2} \frac{n-(p+1)}{p}
\end{align*}
今回の特徴量選択では各特徴量と目的変数の回帰を行っているので、特徴量の数は1となるので$p=1$を代入すると、
F = \frac{R^2}{1 - R^2} (n-2)
という式で表せます。この値は、特徴量である説明変数と目的変数の母相関係数を$\rho$としたときに$\rho = 0$であるという帰無仮説の元では自由度$(1, n- 2)$のF分布に従うことがわかっています(理由が書いてある書籍orサイトが見つからなかった。。)。
この式はscikit-learnのf_regressionの実装と一致していることがわかります。
ちなみに上のf_regression関数の実装を見ると、centerというbool変数があり、これがTrueのときは自由度を1上げているのですが、これはおそらく、centerがTrueのときは回帰式の定数項が0になるために束縛条件が一つ減るからだと思われます。
mutual_info_regression
mutual_info - mutual_info_regression
相互情報量を計算します。mutual_info_classifと同じ特徴です。
参考
- 残差分散
- Multiple Linear Regression
- 東京大学教養学部統計学教室, 1992/8/1, 自然科学の統計学, 東京大学出版会