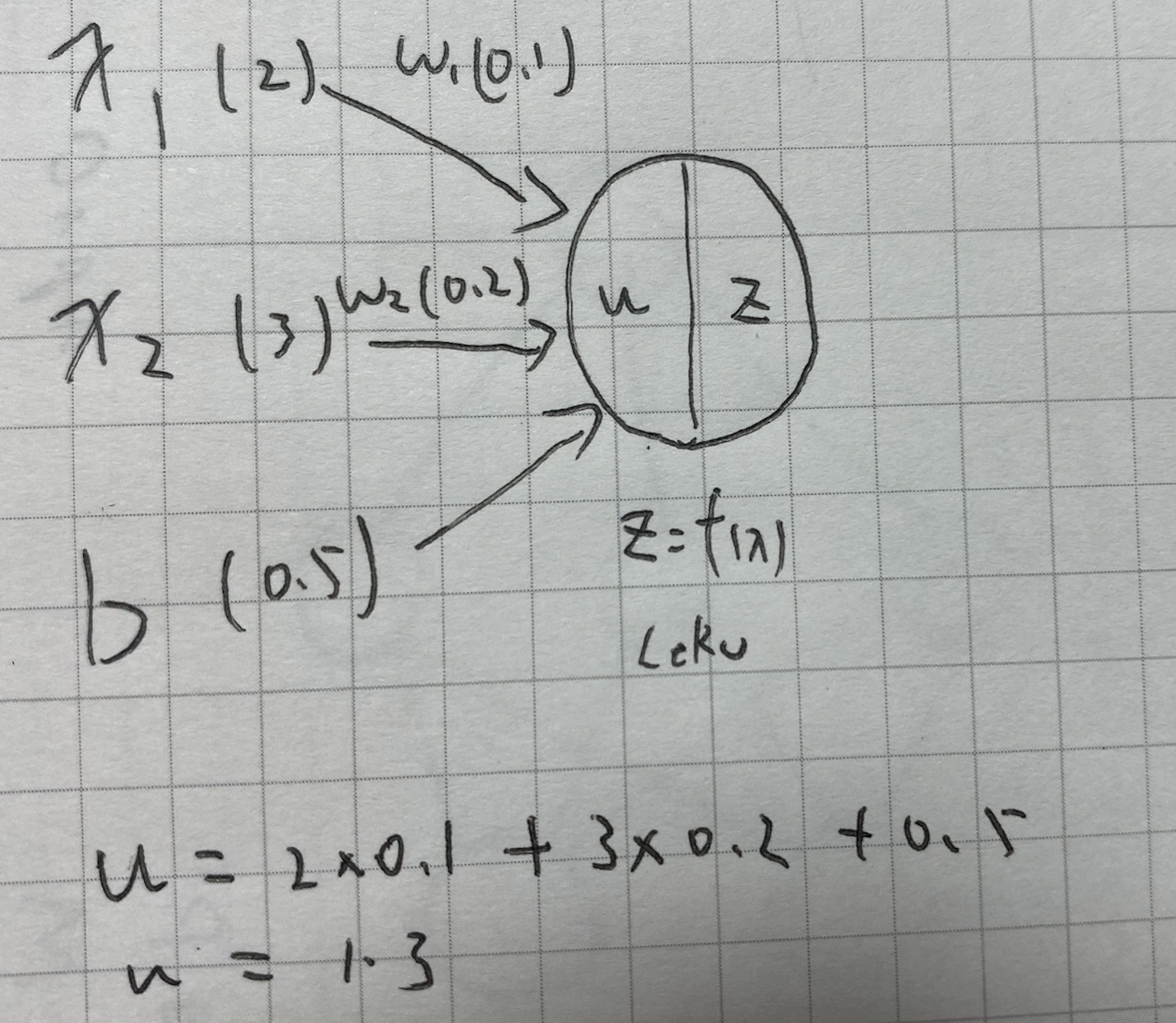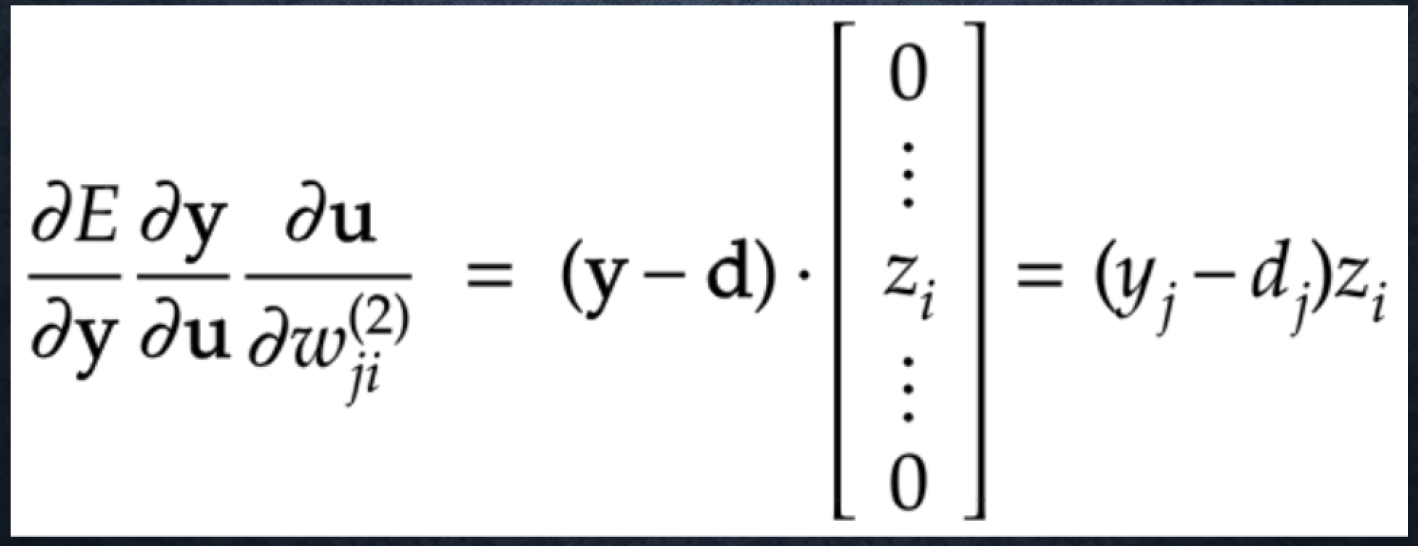Go to Qiita Advent Calendar 2024 Top
LoginSignup

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

This article is a Private article. Only a writer and users who know the URL can access it.
Please change open range to public in publish setting if you want to share this article with other users.

More than 3 years have passed since last update.

@fantahide

【ラビットチャレンジ】深層学習(Day1:Neural Network:NN)

Last updated at Posted at 2020-05-09

E資格取得のためラビットチャレンジに挑戦しています。

#Neural Network:NN
###ポイント

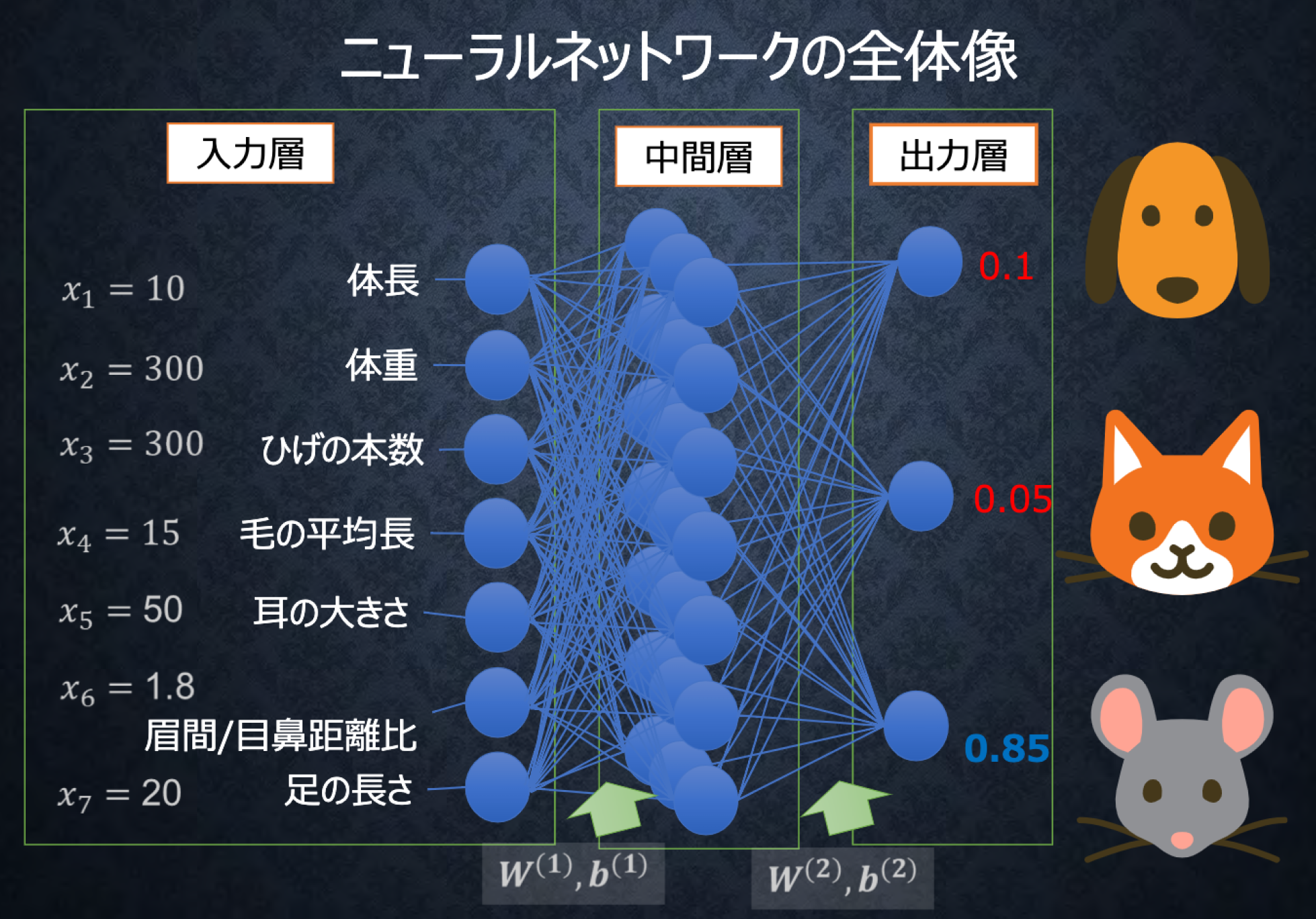
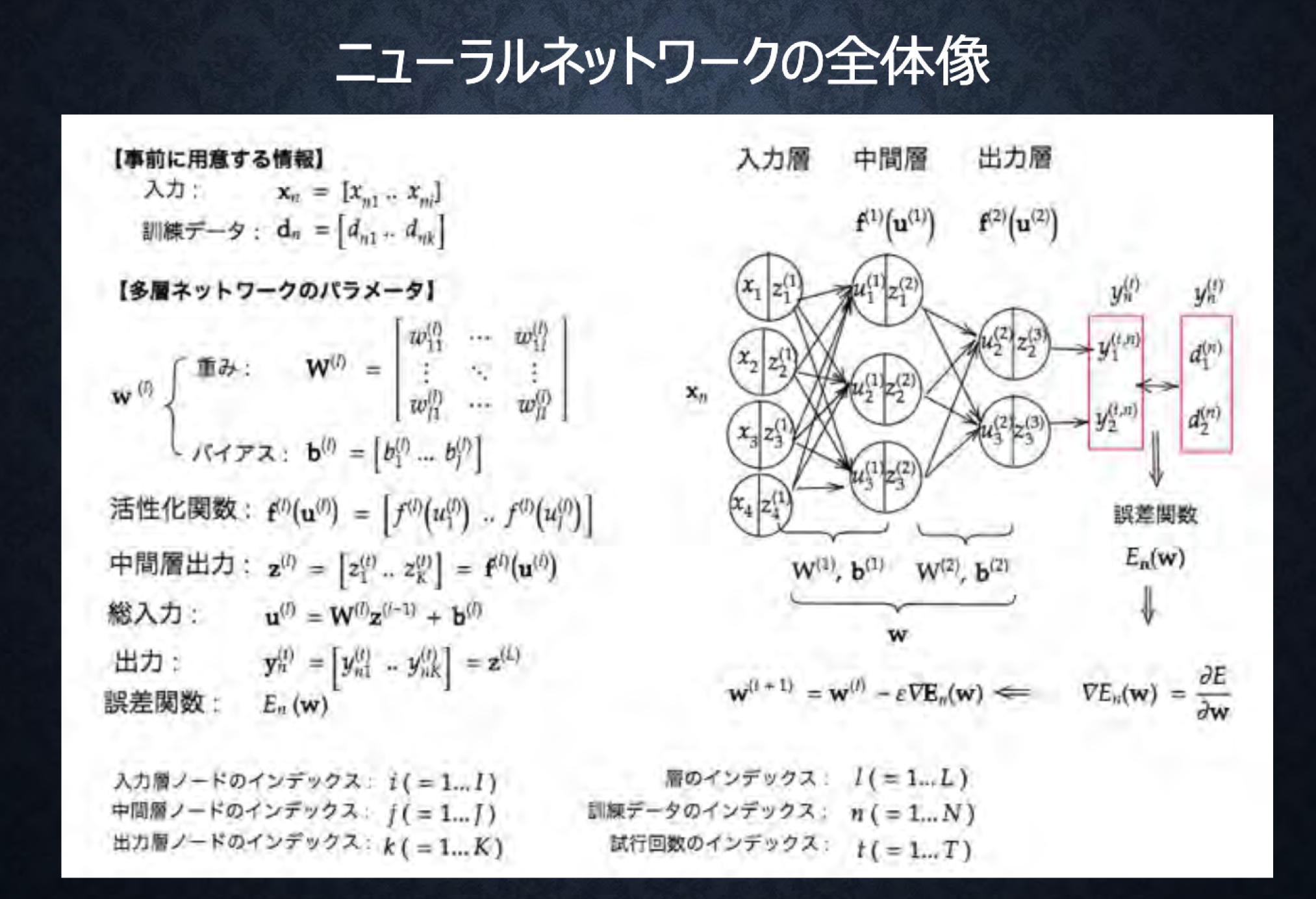
  • 全体像

    • image.png

    • image.png

    • 1.入力層に値を入力

    • 2.重み、バイアス、活性化関数で計算しながら値が伝わる

    • 3.出力層から値が伝わる

    • 4.出力層から出た値と正解値から、誤差関数を使って誤差を求める

    • 5.誤差を小さくするために重みやバイアスを更新する

    • 6.1~5の操作を繰り返すことにより、出力値を正解値に近づけていく

  • できること

    • 回帰
      • 結果予測
        • 売上予想
        • 株価予想
      • ランキング
        • 競馬順位予想
        • 人気順位予想
    • 分類
      • 猫の写真判別
      • 手書きの文字認識
      • 花の種類分類

  • 回帰分析の種類(連続する実数値をとる関数の近似)

    • 線形回帰
    • 回帰木
    • ランダムフォレスト
    • ニューラルネットワーク

  • 分類分析の種類(性別や動物の種類など離散的な結果を予想するための分析)

    • ベイズ分類
    • ロジスティック回帰
    • 決定木
    • ランダムフォレスト
    • ニューラルネットワーク

  • 深層学習の実用例

    • 自動売買(トレード)
    • チャットボット
    • 翻訳
    • 音声解釈
    • 囲碁、将棋AI

#Section1 入力層〜中間層

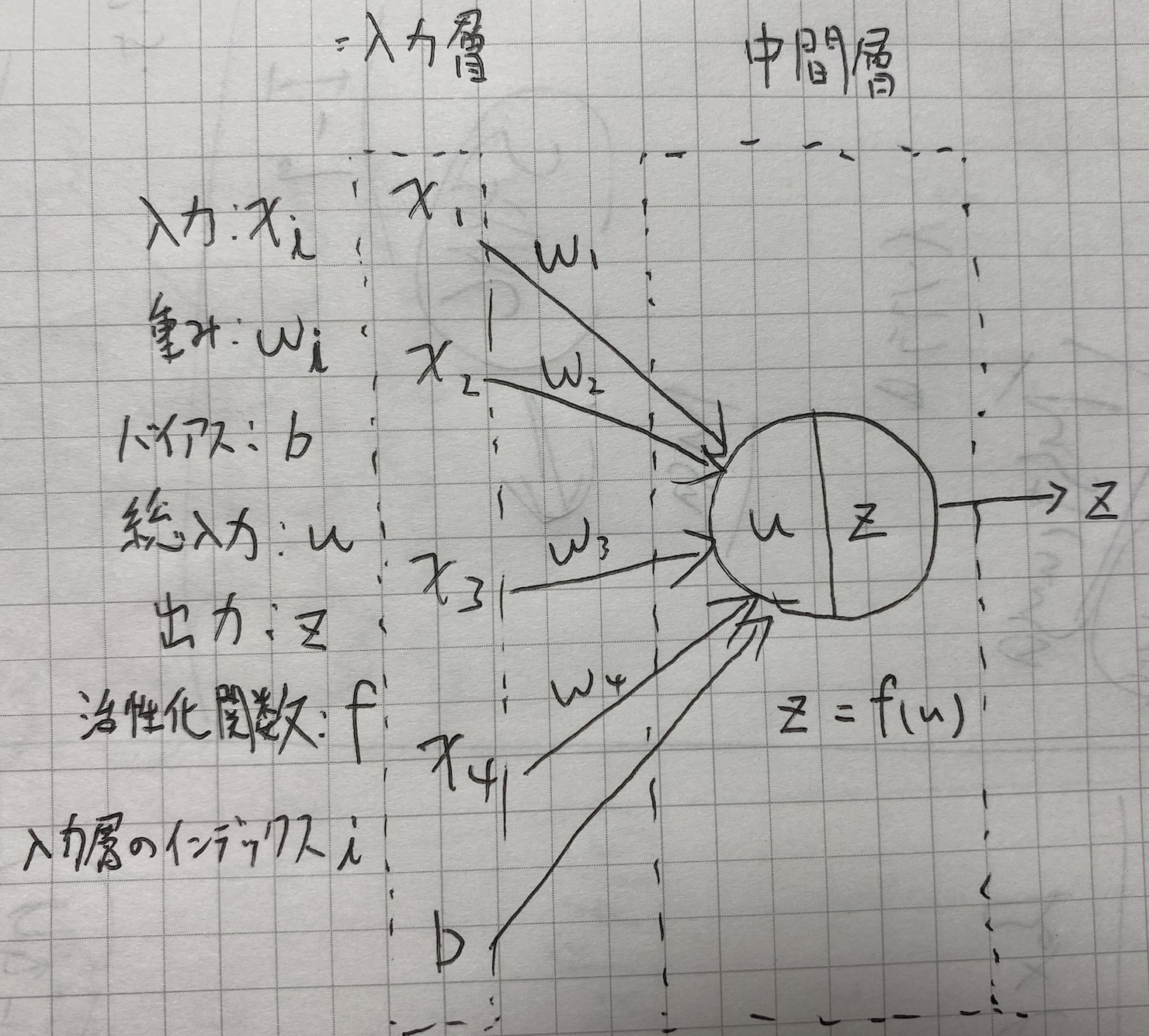
###ポイント

  • 範囲
    • image.png
\boldsymbol W = 
\begin{bmatrix}
w_1  \\\ 
\vdots  \\\
w_i 
\end{bmatrix},
\boldsymbol x = 
\begin{bmatrix}
x_1  \\\ 
\vdots  \\\
x_i 
\end{bmatrix}
..(1,1)
\\
\begin{eqnarray}
u &=& w_1x_1+w_2x_2+w_3x_3+w_4x_4+b
\\&=& Wx+b ..(1,2)

\end{eqnarray}

#####確認テスト

Jupyter
#(1,2)をpythonで表現
#内積
u1 = np.dot(x,W1) + b1
ソースコード名
1_1_forward_propagation.ipynb

#####確認テスト

Jupyter
#確認テスト,中間層の出力を定義しているソースを抜き出す
# 中間層出力
z = functions.relu(u)

###ハンズオン

ソースコード名
1_1_forward_propagation.ipynb

image.png

Jupyter
# 順伝播（単層・単ユニット）

# 重み
W = np.array([[0.1], [0.2]])

## 試してみよう_配列の初期化
#W = np.zeros(2)
#W = np.ones(2)
#W = np.random.rand(2)
#W = np.random.randint(5, size=(2))

print_vec("重み", W)


# バイアス
b = 0.5

## 試してみよう_数値の初期化
#b = np.random.rand() # 0~1のランダム数値
#b = np.random.rand() * 10 -5  # -5~5のランダム数値
#0-4までの乱数を2つ

print_vec("バイアス", b)

# 入力値
x = np.array([2, 3])
print_vec("入力", x)


# 総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = functions.relu(u)
print_vec("中間層出力", z)
出力
*** 重み ***
[[0.1]
 [0.2]]

*** バイアス ***
0.5

*** 入力 ***
[2 3]

*** 総入力 ***
[1.3]

*** 中間層出力 ***
[1.3]

####考察
入力層対して正しい数の重みがあるかどうかが重要。
プログラムエラー原因になる。

####参考
ゼロから作るDeeplearning

#Section2 活性化関数

###ポイント

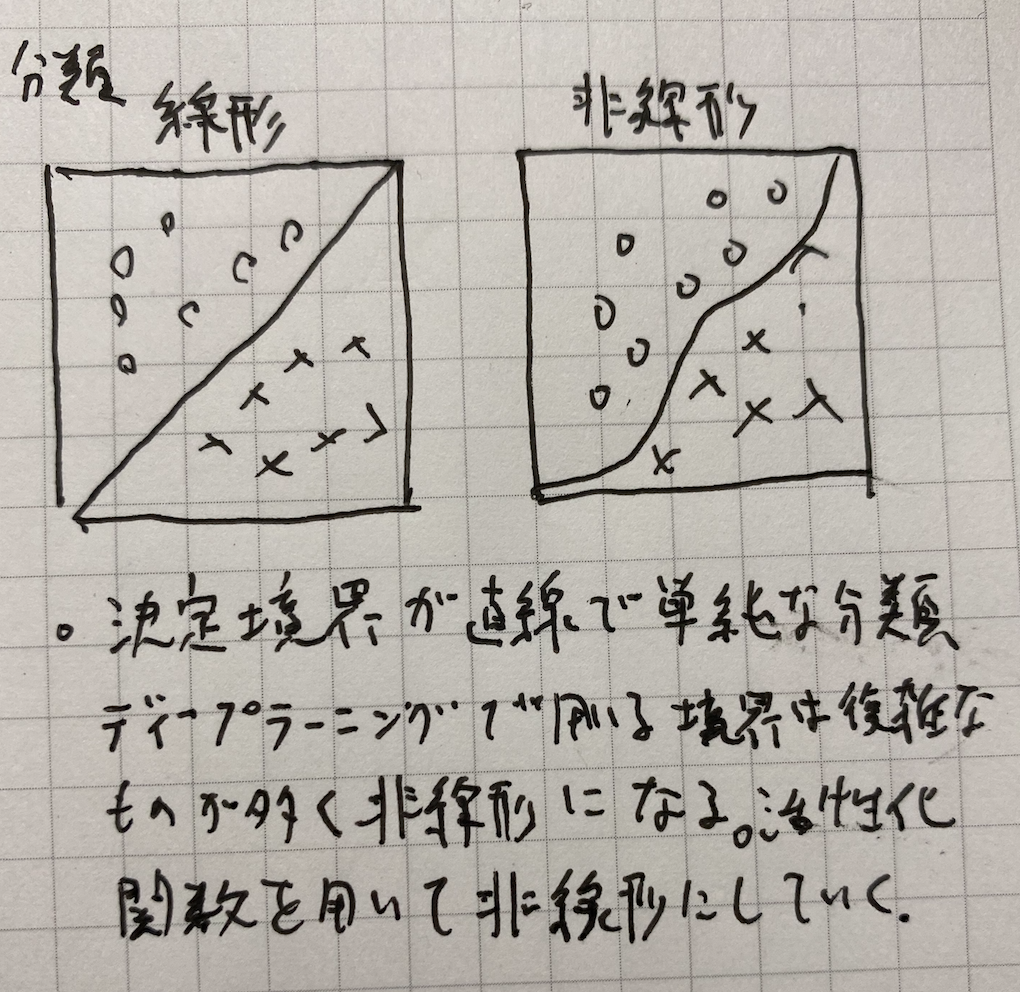
  • ニューラルネットワークにおいて、次の層への出力の大きさを決める非線形の関数

  • 中間層用の活性化関数

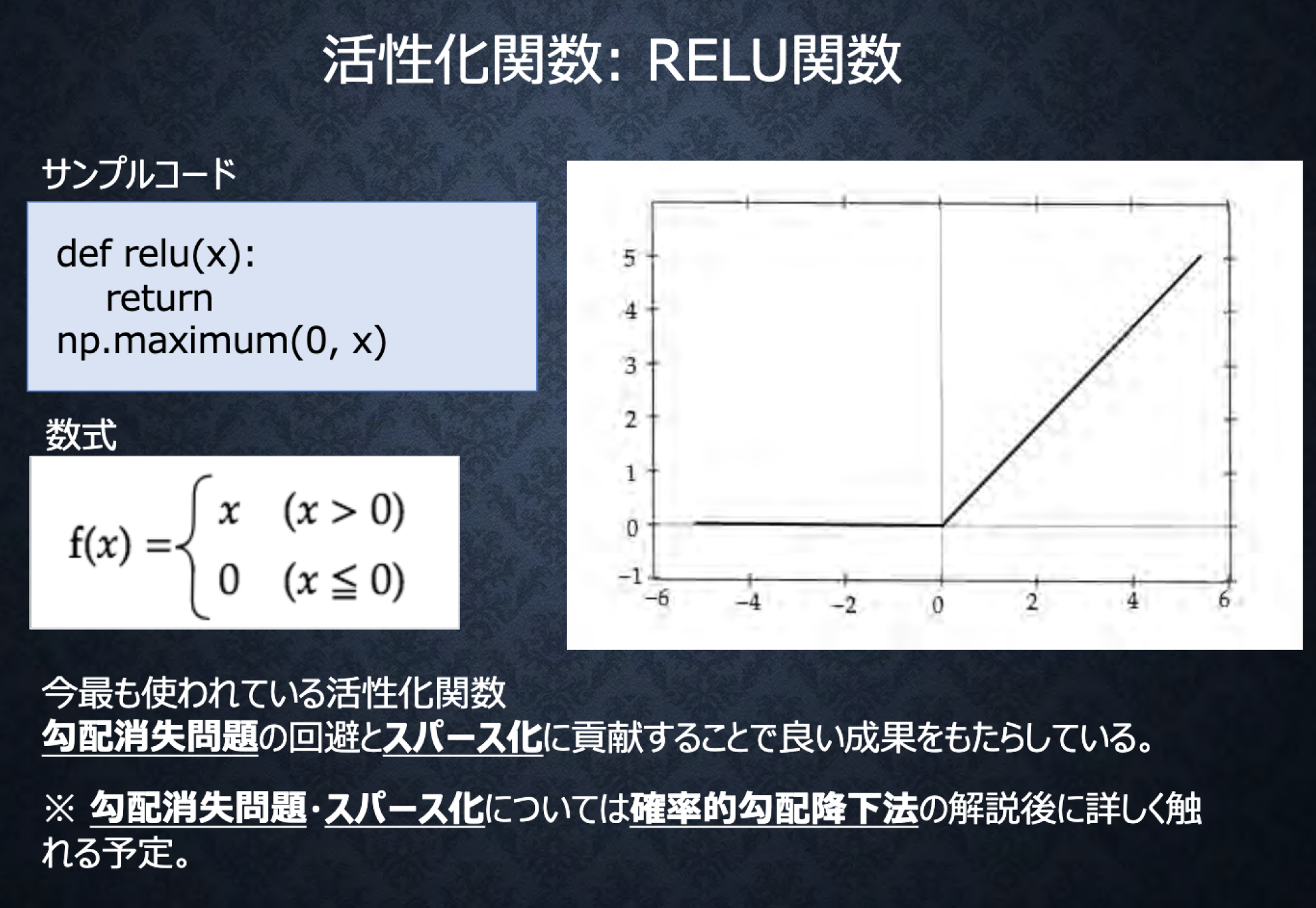
    • ReLu関数
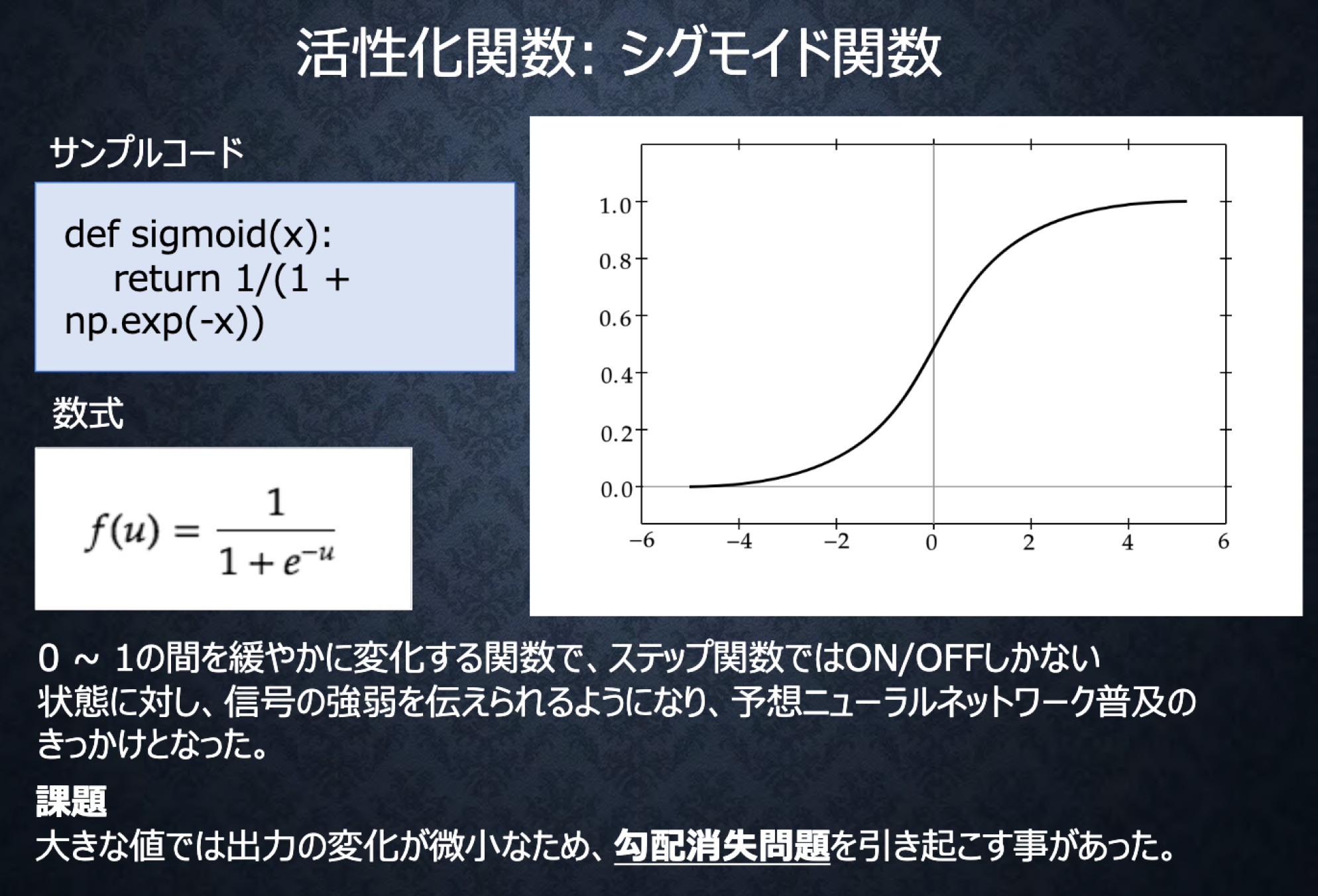
    • シグモイド(ロジスティック)関数
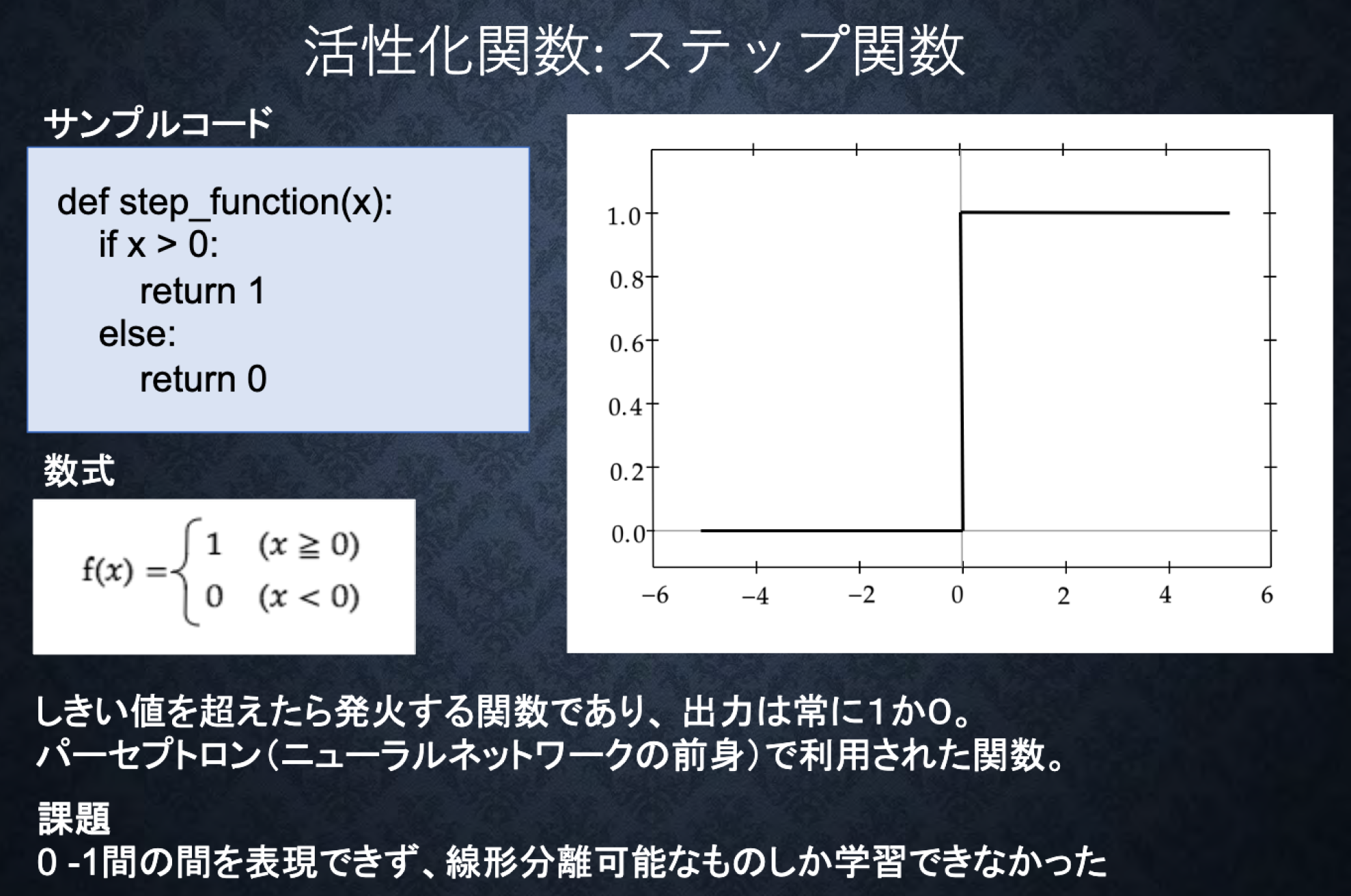
    • ステップ関数(ディープラーニングでは使われない。)

  • 活性化関数

f^{(l)}(u^{(l)}=
\begin{bmatrix} 
f^{(l)}(u_1^{(l)}),\cdots,f^{(l)}(u_j^{(l)})
\end{bmatrix}

image.png

image.png

image.png

#####確認テスト

  • 線形非線形の違いを図に書いて簡易に説明せよ
    image.png

#####確認テスト

Jupyter
#ソースコードより z=f(u)を抜き出す
# 中間層出力
z = functions.sigmoid(u)

# シグモイド関数（ロジスティック関数）
def sigmoid(x):
    return 1/(1 + np.exp(-x))

###ハンズオン

Jupyter

# Sigmoid
# 順伝播（単層・複数ユニット）

# 重み
W = np.array([
    [0.1, 0.2, 0.3], 
    [0.2, 0.3, 0.4], 
    [0.3, 0.4, 0.5],
    [0.4, 0.5, 0.6]
])

## 試してみよう_配列の初期化
#W = np.zeros((4,3))
#W = np.ones((4,3))
#W = np.random.rand(4,3)
#W = np.random.randint(5, size=(4,3))

print_vec("重み", W)

# バイアス
b = np.array([0.1, 0.2, 0.3])
print_vec("バイアス", b)

# 入力値
x = np.array([1.0, 5.0, 2.0, -1.0])
print_vec("入力", x)


#  総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = functions.sigmoid(u)
print_vec("中間層出力", z)
出力
*** 重み ***
[[0.1 0.2 0.3]
 [0.2 0.3 0.4]
 [0.3 0.4 0.5]
 [0.4 0.5 0.6]]

*** バイアス ***
[0.1 0.2 0.3]

*** 入力 ***
[ 1.  5.  2. -1.]

*** 総入力 ***
[1.4 2.2 3. ]

*** 中間層出力 ***
[0.80218389 0.90024951 0.95257413]
Jupyter
# RELU
# 順伝播（単層・複数ユニット）

# 重み
W = np.array([
    [0.1, 0.2, 0.3], 
    [0.2, 0.3, 0.4], 
    [0.3, 0.4, 0.5],
    [0.4, 0.5, 0.6]
])

## 試してみよう_配列の初期化
#W = np.zeros((4,3))
#W = np.ones((4,3))
#W = np.random.rand(4,3)
#W = np.random.randint(5, size=(4,3))

print_vec("重み", W)

# バイアス
b = np.array([0.1, 0.2, 0.3])
print_vec("バイアス", b)

# 入力値
x = np.array([1.0, 5.0, 2.0, -1.0])
print_vec("入力", x)


#  総入力
u = np.dot(x, W) + b
print_vec("総入力", u)

# 中間層出力
z = functions.relu(u)
print_vec("中間層出力", z)
出力
*** 重み ***
[[0.1 0.2 0.3]
 [0.2 0.3 0.4]
 [0.3 0.4 0.5]
 [0.4 0.5 0.6]]

*** バイアス ***
[0.1 0.2 0.3]

*** 入力 ***
[ 1.  5.  2. -1.]

*** 総入力 ***
[1.4 2.2 3. ]

*** 中間層出力 ***
[1.4 2.2 3. ]

####考察
プログラミングを行う際は毎度関数の定義をするわけではなく、
演習ソースコードのように関数をまとめたファイルを作成し、importした方が便利だと思った。
中間層の出力を比べると、SigmoidよりRelu方が、シンプルな値になる、これは数式から明らかである。
今回0以下の総入力がなかったため、総入力と中間層出力は同じ値になっている。

####参考
ゼロから作るDeeplearning

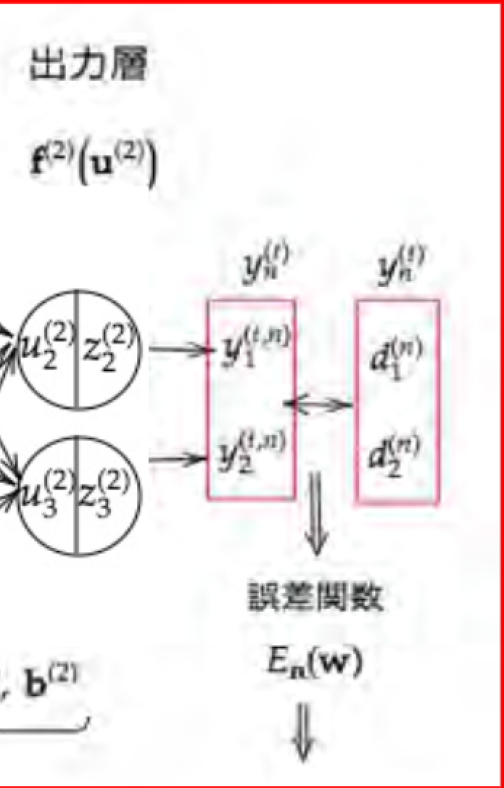
#Section3 出力層

  • image.png

##3-1誤差関数
###ポイント

  • 出力データと訓練データから算出する
  • 誤差をどんどん小さくしていく
  • 分類問題では二乗誤差は使われない。

#####確認テスト

  • $E_n(w)= \frac{1}{2}\sum_{j=1}^{l}(y_i-d_j)^2 = \frac{1}{2}||(y-d)||^2$
  • なぜ引き算ではなく二乗するのか述べよ
  • マイナス値を扱わないため
  • 1/2はどのような意味を持つのか述べよ
  • 微分の計算を簡単にするため

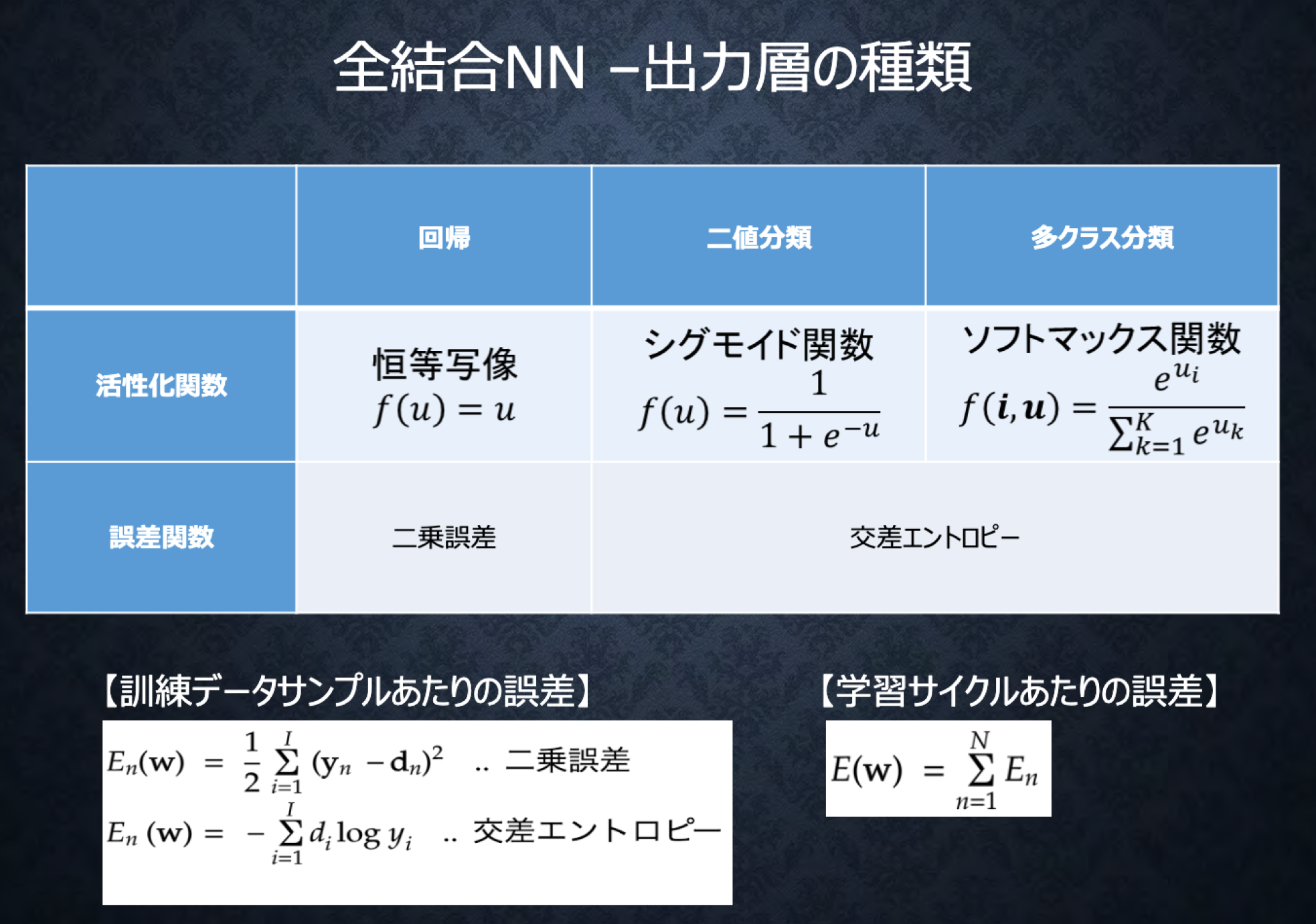
##3-2出力層の活性化関数
###ポイント

  • 出力層と中間層で使われる活性化関数は異なる。

  • 出力層用の活性化関数

    • ソフトマックス関数
    • 恒等写像
    • シグモイド関数(ロジスティック関数)

  • image.png

#####確認テスト
$f(i,u) = \frac{e^{u_{i}}}{\sum_{k=1}^{K}e^{u_{k}}}$

image.png

Jupyter
# ソフトマックス関数
def softmax(x):
    if x.ndim == 2: #2次元用
        x = x.T　#xの値を転置させる
        x = x - np.max(x, axis=0) #xの値(ベクトル)のmax値を減算。*np.max(x, axis=0)は列の最大要素を取り出す。
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
#np.exp(x)が②に該当
#np.sum(np.exp(x), axis=0)が③に該当
        return y.T　#yを転置、①に該当


    x = x - np.max(x) # オーバーフロー対策
    return np.exp(x) / np.sum(np.exp(x))

#####確認テスト

image.png

Jupyter
# クロスエントロピー
def cross_entropy_error(d, y):
    if y.ndim == 1:　#1次元用
        d = d.reshape(1, d.size) #1行d列に成形
        y = y.reshape(1, y.size) #1行d列に成形
        
    # 教師データがone-hot-vectorの場合、正解ラベルのインデックスに変換
    #One-hot-vectorは、(0,1,0,0,0,0) のように、1つの成分が1で残りの成分が全て0であるようなベクトルのこと
    if d.size == y.size: # dとyの要素数を比較 *sizeは行列の全要素数出す
        d = d.argmax(axis=1) #列方向(行ごとに)最大の値があるインデックスをdに入れる
    batch_size = y.shape[0] #yの行の数をbatch_sizeに入れる。
    return -np.sum(np.log(y[np.arange(batch_size), d] + 1e-7)) / batch_size　#②
#1e-7は分子が0にならないように微小な値をいれて調整している。

####考察
回帰や分類に置いて有効な活性化関数と誤差関数の組み合わせがある。

####参考
https://python.atelierkobato.com/max/
https://deepage.net/features/numpy-argmax.html
https://teratail.com/questions/119233
https://note.nkmk.me/python-numpy-arange-linspace/
https://mathwords.net/onehot

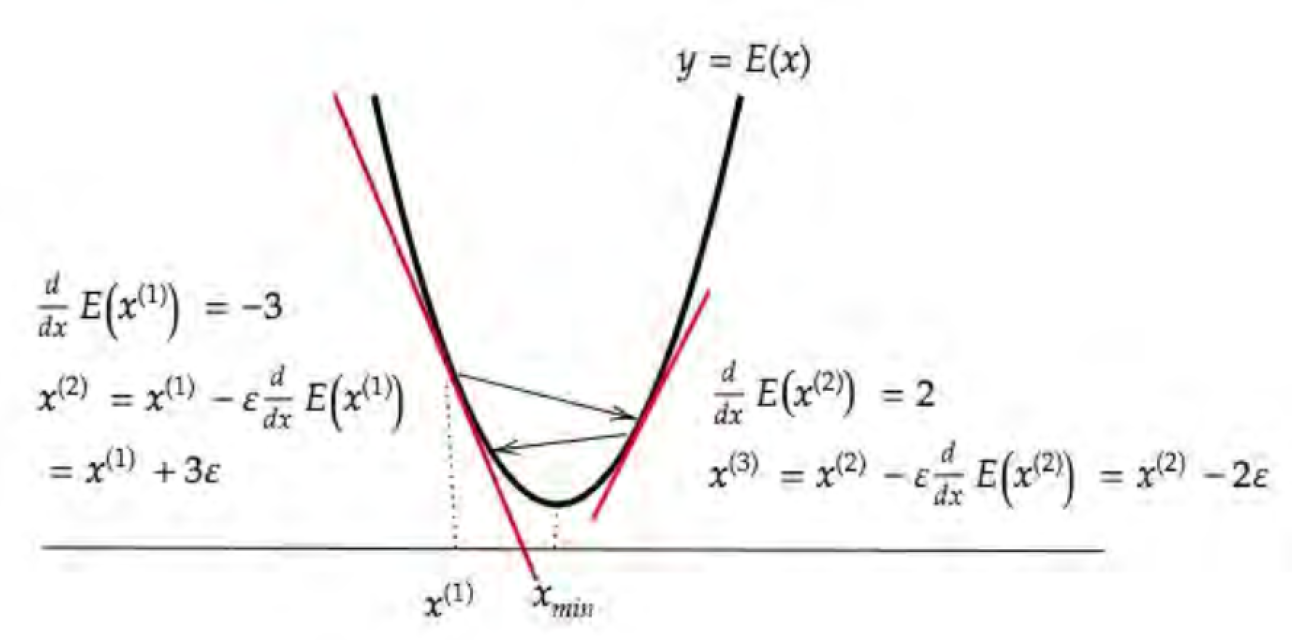
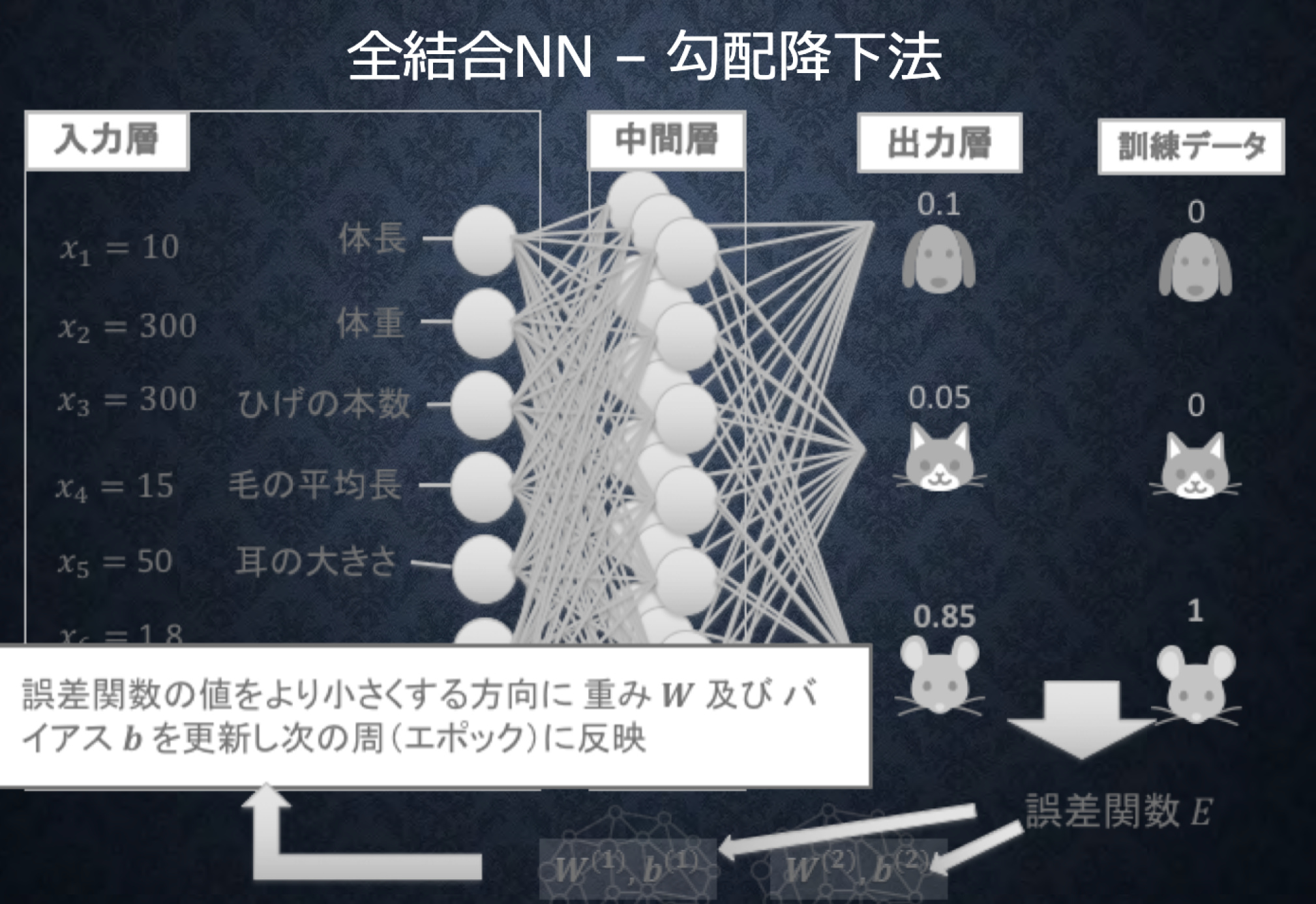
#Section4 勾配降下法
##勾配降下法

w^{(t+1)} = w^{(t)}- \epsilon\nabla E
\\
\epsilon:学習率
\\
\nabla E = \frac{\partial E}{\partial w} = \begin{bmatrix} \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \end{bmatrix}

image.png

###ポイント

  • 誤差$E(w)$を最小化するパラメータ$w$を発見する
  • 全サンプルの平均誤差
  • 学習率$\epsilon$の値によって学習の効率が大きく異なる
  • 学習率が大きすぎる場合、最小値にいつまでもたどり着かず発散する
  • 学習率が小さい場合発散することはないが、小さすぎると収束するまでに時間がかかる。
  • 学習率が小さすぎると局所的最適解に収束することがある(<=>大域的最適解)
  • 学習方法決定、収束性向上のためのアルゴリズム例(論文が多い=課題が多い)
    • Momentum
    • AdaGrad
    • Adadelta
    • Adam
      image.png

#####確認テスト

  • 対応するソースコードを探す
w^{(t+1)} = w^{(t)}- \epsilon\nabla E
\\
\epsilon:学習率
\\
\nabla E = \frac{\partial E}{\partial w} = \begin{bmatrix} \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \end{bmatrix}
Jupyter

#1_2_back_propagation ソースコード
#w^{(t+1)}
network[key]  -= learning_rate * grad[key]

#\nabla E
grad = backward(x, d, z1, y)

#====================
#  学習率
learning_rate = 0.01
#関数
# 誤差逆伝播

def backward(x, d, z1, y):
    print("\n##### 誤差逆伝播開始 #####")

    grad = {}

    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    #  出力層でのデルタ
    delta2 = functions.d_sigmoid_with_loss(d, y)
    #  b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    #  W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    #  中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    #  W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
        
    print_vec("偏微分_dE/du2", delta2)
    print_vec("偏微分_dE/du2", delta1)

    print_vec("偏微分_重み1", grad["W1"])
    print_vec("偏微分_重み2", grad["W2"])
    print_vec("偏微分_バイアス1", grad["b1"])
    print_vec("偏微分_バイアス2", grad["b2"])

    return grad

##確率的勾配降下法(SGD)

w^{(t+1)} = w^{(t)}- \epsilon\nabla E_n

###ポイント

  • ランダムに抽出したサンプルの誤差を測定
  • メリット
    • データが冗長な場合の計算コストの軽減
    • 望まない局所最小解に収束するリスクの軽減
    • オンライン学習ができる

#####確認テスト

  • オンライン学習とは何か2行でまとめよ

入力されるデータ1つ1つに対して学習を行い更新をしていく手法。局所最適解に陥りにくいが、外れ値の影響を受けやすい。

##ミニバッチ勾配降下法

w^{(t+1)} = w^{(t)}- \epsilon\nabla E_t
\\
E_t = \frac {1}{N_t}\sum_{n \in D_t} E_n

N_t = |D_t|

###ポイント

  • ランダムに分割したデータの集合(ミニバッチ)$D_t$に属するサンプルの平均誤差
  • メリット
    • 確率的勾配降下法のメリットを損なわず、計算機の計算資源を有効活用できる->並列化

#####確認テスト

  • 数式の意味を図に書いて説明せよ
w^{(t+1)} = w^{(t)}- \epsilon\nabla E_t

image.png

##誤差勾配の計算

\nabla E = \frac{\partial E}{\partial w} = \begin{bmatrix} \frac{\partial E}{\partial w_1} \cdots \frac{\partial E}{\partial w_M} \end{bmatrix}
  • 数値微分
    • プログラムで微小な数値を生成し擬似的に微分計算をする
    • 各パラメータ$W_M$それぞれについて$E(w_m+h)$や$E(w_m-h)$を計算すために、順伝播の計算を繰り返し行う必要があり負荷が大きい
\frac{\partial E}{\partial w_m} \approx  \frac{E(w_m + h)- E(w_m - h)}{2h}

＝＞　誤差逆伝播法を利用する

####考察
勾配を計算するために様々な手法が用いられているが、現段階ではミニバッチ法が局所最適解に陥りづらく計算コストも少ない。

####参考
https://dev.classmethod.jp/articles/online-batch-learning/
https://to-kei.net/basic-study/neural-network/sgd/

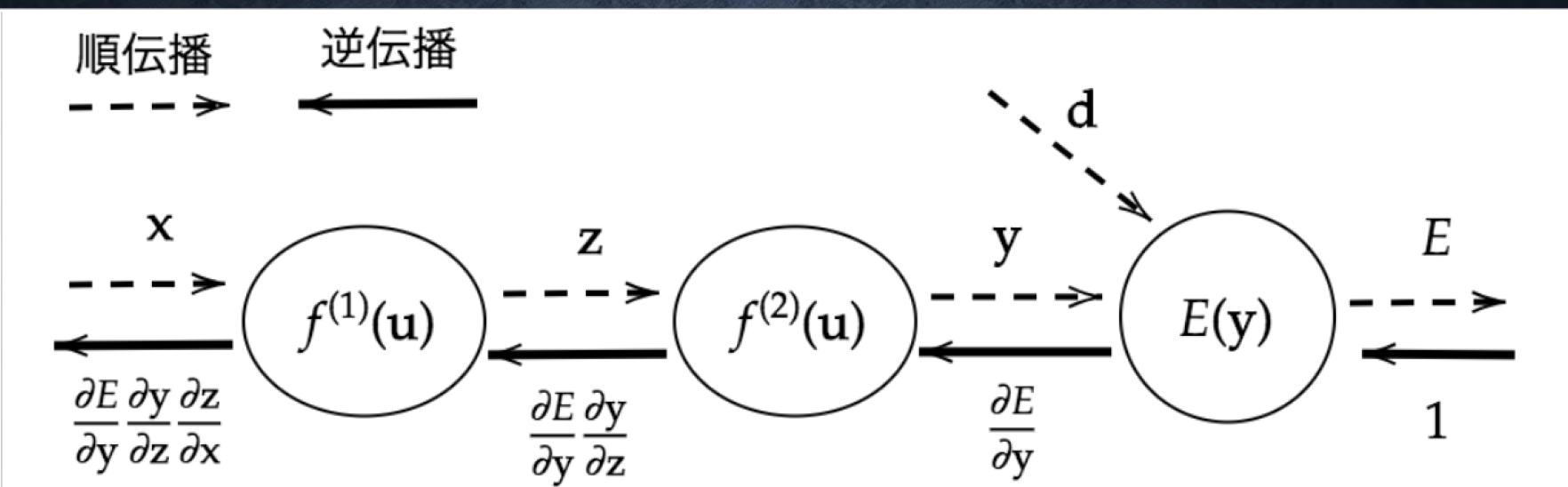
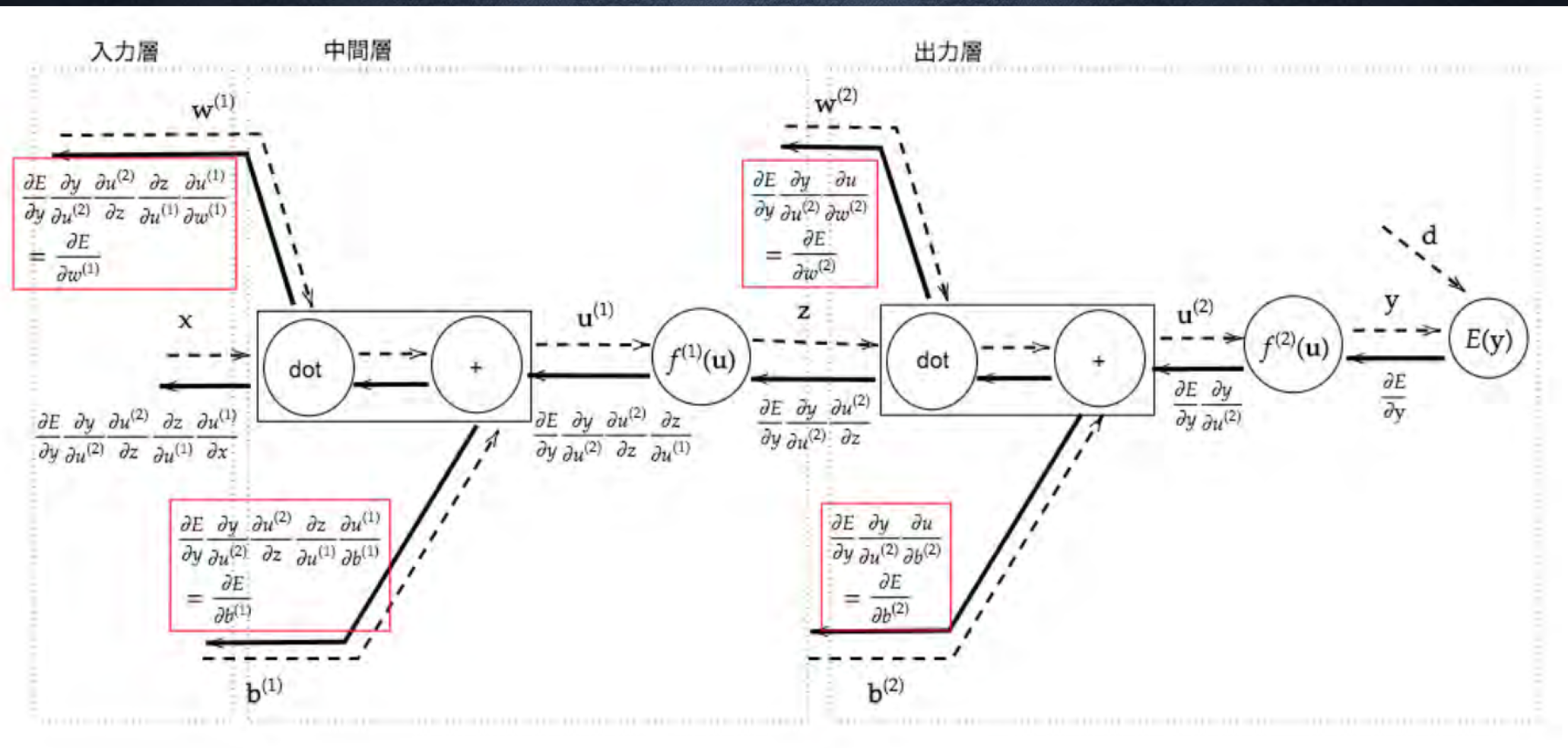
#Section5 誤差逆伝播法
###ポイント

  • 算出された誤差を、出力側から順を微分し、前の層前の層へと伝播させる
  • 最小限の計算で各パラメータでの微分値を解析的に計算する手法
  • 計算結果(=誤差)から微分を逆算することで、不要な再帰的計算を避けて微分算出可能

image.png

image.png

#####確認テスト

  • 誤差逆伝播法では不要な再帰的処理を避けることができる。すでに行なった計算結果を保持しているソースコードを抽出せよ。
Jupyter
# 誤差逆伝播
def backward(x, d, z1, y):
    print("\n##### 誤差逆伝播開始 #####")

    grad = {}

    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    #  出力層でのデルタ
#シグモイドと交差エントロピーの複合導関数
    delta2 = functions.d_sigmoid_with_loss(d, y)
    #  b2の勾配
# delta2が1×2の行列。ベクトル化に変換2
    grad['b2'] = np.sum(delta2, axis=0)
    #  W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    #  中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    #  W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
        
    print_vec("偏微分_dE/du2", delta2)
    print_vec("偏微分_dE/du2", delta1)

    print_vec("偏微分_重み1", grad["W1"])
    print_vec("偏微分_重み2", grad["W2"])
    print_vec("偏微分_バイアス1", grad["b1"])
    print_vec("偏微分_バイアス2", grad["b2"])

    return grad
  • 合成関数の微分で求めることが可能
    image.png
    image.png

###ハンズオン

ソースコード名
1_3_stochastic_gradient_descent
Jupyter

# 確率勾配降下法
# Relu関数

import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common import functions
import matplotlib.pyplot as plt

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    #print("shape: " + str(x.shape))
    print("")

# サンプルとする関数
#yの値を予想するAI

def f(x):
    y = 3 * x[0] + 2 * x[1]
    return y

# 初期設定
def init_network():
    # print("##### ネットワークの初期化 #####")
    network = {}
    nodesNum = 10
    network['W1'] = np.random.randn(2, nodesNum)
    network['W2'] = np.random.randn(nodesNum)
    network['b1'] = np.random.randn(nodesNum)
    network['b2'] = np.random.randn()

    # print_vec("重み1", network['W1'])
    # print_vec("重み2", network['W2'])
    # print_vec("バイアス1", network['b1'])
    # print_vec("バイアス2", network['b2'])

    return network

# 順伝播
def forward(network, x):
    # print("##### 順伝播開始 #####")
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    u1 = np.dot(x, W1) + b1
    z1 = functions.relu(u1)
    
    ## 試してみよう
    #z1 = functions.sigmoid(u1)
    
    u2 = np.dot(z1, W2) + b2
    y = u2

    # print_vec("総入力1", u1)
    # print_vec("中間層出力1", z1)
    # print_vec("総入力2", u2)
    # print_vec("出力1", y)
    # print("出力合計: " + str(np.sum(y)))    
    
    return z1, y

# 誤差逆伝播
def backward(x, d, z1, y):
    # print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 中間層でのデルタ
    delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)

    ## 試してみよう
    # delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
    # print_vec("偏微分_重み1", grad["W1"])
    # print_vec("偏微分_重み2", grad["W2"])
    # print_vec("偏微分_バイアス1", grad["b1"])
    # print_vec("偏微分_バイアス2", grad["b2"])

    return grad

# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]

for i in range(data_sets_size):
    data_sets[i] = {}
    # ランダムな値を設定
    data_sets[i]['x'] = np.random.rand(2)
    
    ## 試してみよう_入力値の設定
    # data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
    
    # 目標出力を設定
    data_sets[i]['d'] = f(data_sets[i]['x'])
    
losses = []
# 学習率
learning_rate = 0.07

# 抽出数
epoch = 1000

# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)

# 勾配降下の繰り返し
for dataset in random_datasets:
    x, d = dataset['x'], dataset['d']
    z1, y = forward(network, x)
    grad = backward(x, d, z1, y)
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key]

    # 誤差
    loss = functions.mean_squared_error(d, y)
    losses.append(loss)

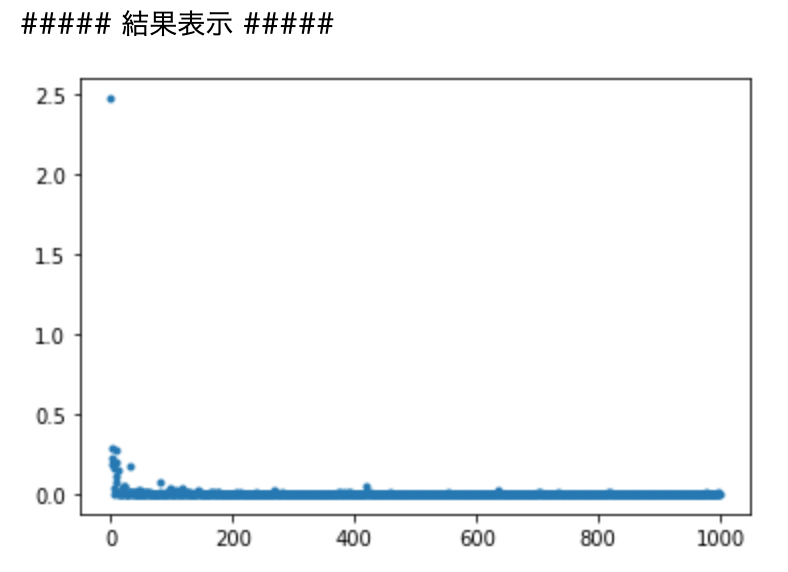
print("##### 結果表示 #####")    
lists = range(epoch)


plt.plot(lists, losses, '.')
# グラフの表示
plt.show()

image.png

Jupyter

# 確率勾配降下法
# シグモイド関数


import sys, os
sys.path.append(os.pardir)  # 親ディレクトリのファイルをインポートするための設定
import numpy as np
from common import functions
import matplotlib.pyplot as plt

def print_vec(text, vec):
    print("*** " + text + " ***")
    print(vec)
    #print("shape: " + str(x.shape))
    print("")

# サンプルとする関数
#yの値を予想するAI

def f(x):
    y = 3 * x[0] + 2 * x[1]
    return y

# 初期設定
def init_network():
    # print("##### ネットワークの初期化 #####")
    network = {}
    nodesNum = 10
    network['W1'] = np.random.randn(2, nodesNum) #2×10の0-1の乱数
    network['W2'] = np.random.randn(nodesNum) #10この乱数
    network['b1'] = np.random.randn(nodesNum)
    network['b2'] = np.random.randn()

    #print_vec("重み1", network['W1'])
    #print_vec("重み2", network['W2'])
    #print_vec("バイアス1", network['b1'])
    #print_vec("バイアス2", network['b2'])

    return network

# 順伝播
def forward(network, x):
    # print("##### 順伝播開始 #####")
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']
    u1 = np.dot(x, W1) + b1
    #z1 = functions.relu(u1)
    
    ## 試してみよう
    z1 = functions.sigmoid(u1)
    
    u2 = np.dot(z1, W2) + b2
    y = u2

    #print_vec("総入力1", u1)
    #print_vec("中間層出力1", z1)
    #print_vec("総入力2", u2)
    #print_vec("出力1", y)
    #print("出力合計: " + str(np.sum(y)))    
    
    return z1, y

# 誤差逆伝播
def backward(x, d, z1, y):
    #print("\n##### 誤差逆伝播開始 #####")    

    grad = {}
    
    W1, W2 = network['W1'], network['W2']
    b1, b2 = network['b1'], network['b2']

    # 出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)
    # b2の勾配
    grad['b2'] = np.sum(delta2, axis=0)
    # W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)
    # 中間層でのデルタ
    #delta1 = np.dot(delta2, W2.T) * functions.d_relu(z1)

    ## 試してみよう
    delta1 = np.dot(delta2, W2.T) * functions.d_sigmoid(z1)

    delta1 = delta1[np.newaxis, :]
    # b1の勾配
    grad['b1'] = np.sum(delta1, axis=0)
    x = x[np.newaxis, :]
    # W1の勾配
    grad['W1'] = np.dot(x.T, delta1)
    
    # print_vec("偏微分_重み1", grad["W1"])
    # print_vec("偏微分_重み2", grad["W2"])
    # print_vec("偏微分_バイアス1", grad["b1"])
    # print_vec("偏微分_バイアス2", grad["b2"])

    return grad

# サンプルデータを作成
data_sets_size = 100000
data_sets = [0 for i in range(data_sets_size)]

for i in range(data_sets_size):
    data_sets[i] = {}
    # ランダムな値を設定
    data_sets[i]['x'] = np.random.rand(2)
    
    ## 試してみよう_入力値の設定
    # data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
    
    # 目標出力を設定
    data_sets[i]['d'] = f(data_sets[i]['x'])
    
losses = []
# 学習率
learning_rate = 0.07

# 抽出数
epoch = 1000

# パラメータの初期化
network = init_network()
# データのランダム抽出
random_datasets = np.random.choice(data_sets, epoch)

# 勾配降下の繰り返し
for dataset in random_datasets:
    x, d = dataset['x'], dataset['d']
    z1, y = forward(network, x)
    grad = backward(x, d, z1, y)
    # パラメータに勾配適用
    for key in ('W1', 'W2', 'b1', 'b2'):
        network[key]  -= learning_rate * grad[key]

    # 誤差
    loss = functions.mean_squared_error(d, y)
    losses.append(loss)

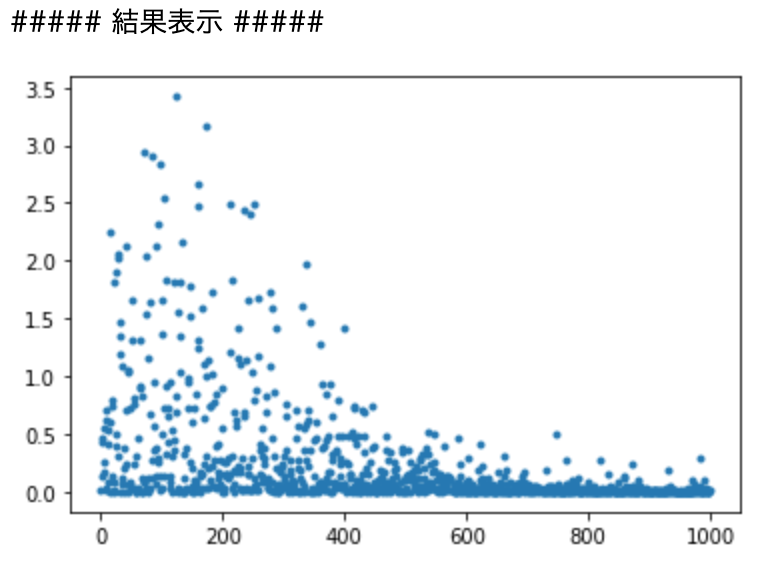
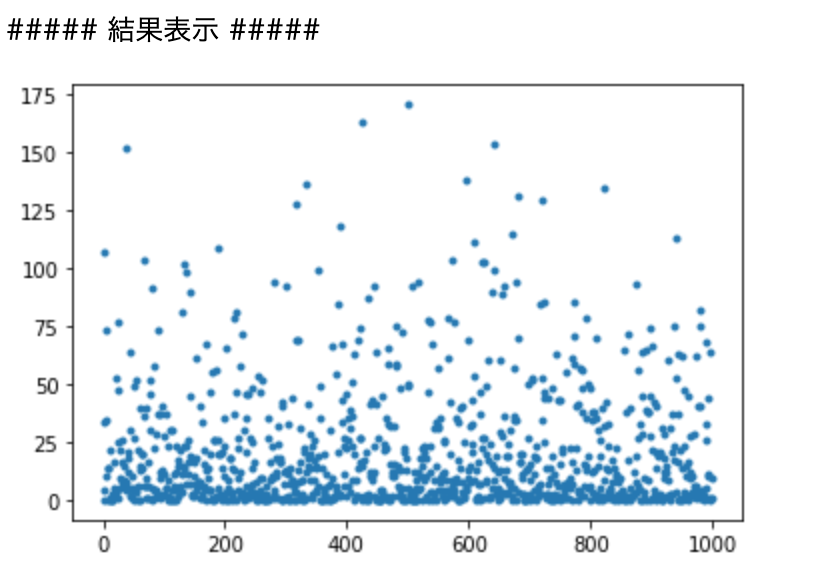
print("##### 結果表示 #####")    
lists = range(epoch)


plt.plot(lists, losses, '.')
# グラフの表示
plt.show()

image.png

Jupyter
#デルタのランダム数を変更した場合
# ランダムな値を設定
    # data_sets[i]['x'] = np.random.rand(2) #0-1のランダム数
    
    ## 試してみよう_入力値の設定
    data_sets[i]['x'] = np.random.rand(2) * 10 -5 # -5〜5のランダム数値
  • シグモイド
    image.png

#####確認テスト

  • 該当するソースコードを抽出せよ。
\frac{\partial E}{\partial y} ・・・①
\\
\frac{\partial E}{\partial y}\frac{\partial y}{\partial u} ・・・②
\\
\frac{\partial E}{\partial y}\frac{\partial y}{\partial u}\frac{\partial u}{\partial w_{ji}^{(2)}}　・・・③
Jupyter
# ①出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)

# ②出力層でのデルタ
    delta2 = functions.d_mean_squared_error(d, y)

# ③W2の勾配
    grad['W2'] = np.dot(z1.T, delta2)

②は$\frac{\partial y}{\partial u} = 1$であることに注意。

####考察
各epoch毎の二乗誤差をだしている。
Relu関数よりシグモイドの方が誤差にばらつきがある。また入力の乱数の幅を広げると
その分二乗誤差が大きくなっている。

####参考
ゼロから作るDeeplearning

0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?