前回の単純パーセプトロンの理論と実装で、入力と期待する出力さえ与えればAND回路を作れることを確認し、どのような仕組みで重みとバイアス項が適切な値に近づくのかが理解できたと思います。
では、単純パーセプトロンで如何なる問題も、入力と期待する出力さえあれば解けるのでしょうか?
今回の記事ではその部分を説明していきます。
単純パーセプトロンの限界
さて、とりあえず何も考えずに色々な回路を単純パーセプトロンで作ってみましょう。
今回のコードはここに置いています。
前回とSimplePerceptronクラスは変更なしです。
今回は期待する出力を以下のように定義しましょう。
# 入力と出力のデータを作成
X = np.array([[0,0],[0,1],[1,0],[1,1]])
Y_OR = np.array([[0],[1],[1],[1]])
Y_AND = np.array([[0],[0],[0],[1]])
Y_NAND = np.array([[1],[1],[1],[0]])
Y_XOR = np.array([[0],[1],[1],[0]])
そして、単純パーセプトロンクラスの Fit()に入力と期待する出力を渡して動作させます。
# OR回路
l_OR = SP.Fit(X, Y_OR)
# AND回路
l_AND = SP.Fit(X, Y_AND)
# NAND回路
l_NAND = SP.Fit(X, Y_NAND)
# XOR回路
l_XOR = SP.Fit(X, Y_XOR)
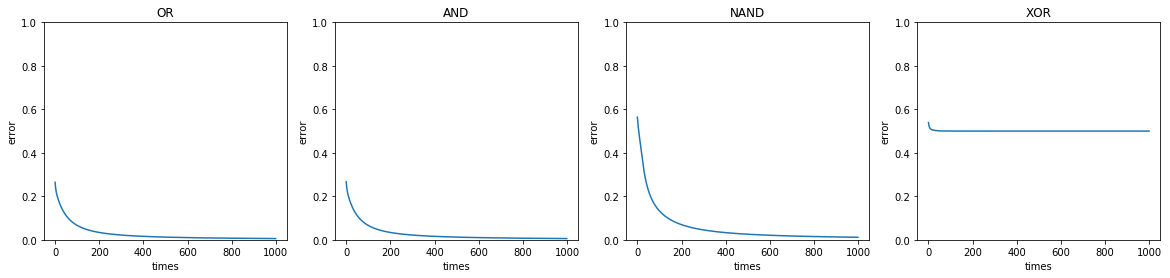
では、誤差の推移を確認してみましょう。
plt.figure(figsize=(20, 4))
plt.subplot(1,4,1)
plt.plot(l_OR)
plt.xlabel("times")
plt.ylabel("error")
plt.ylim(0, 1)
plt.title("OR")
plt.subplot(1,4,2)
plt.plot(l_AND)
plt.xlabel("times")
plt.ylabel("error")
plt.ylim(0, 1)
plt.title("AND")
plt.subplot(1,4,3)
plt.plot(l_NAND)
plt.xlabel("times")
plt.ylabel("error")
plt.ylim(0, 1)
plt.title("NAND")
plt.subplot(1,4,4)
plt.plot(l_XOR)
plt.xlabel("times")
plt.ylabel("error")
plt.ylim(0, 1)
plt.title("XOR")
それぞれの学習回数における出力誤差が表示されていますが、XORだけ誤差が0.5より小さくなっていません。
XOR回路は真理値表では以下の回路です。
| $x_1$ | $x_2$ | 期待する出力 |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
実際に学習後のXOR回路を使って、どのような値を出力するか以下のコードで確認してみましょう。
SP.Forward(X)
上記を実行すると以下の通り、確かに期待する出力にはなっていません。
array([[0.],
[0.],
[0.],
[1.]])
では OR回路などの単純パーセプトロンで解ける回路と、XOR回路などの解けない回路を並べて違いがあるか見比べてみることにします。
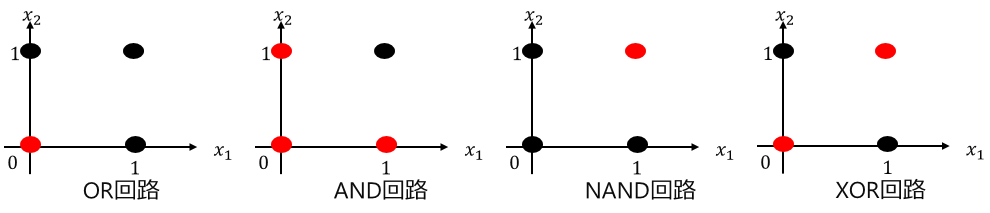
赤丸が出力0を示し、黒丸が出力1を示します。
一見すると OR/AND/NAND回路そして XOR回路で違いはないように思えますが、XOR回路だけ赤丸と黒丸がどちらか一方に固まっていないということがわかります。そうです、それが答えです。
単純パーセプトロンで解ける問題というのは、線形分離可能な問題のみです。
XOR回路の様に線形分離不可能な問題は解くことが出来ません。なお、線形分離可能とは、
幾何学においてふたつの点の集合が二次元平面上にあるとき、それらの集合を一本の直線で分離できることをいいます。これを一般化して、n次元空間上のふたつの点の集合をn-1次元の超平面で分離できることも線形分離可能と呼びます(Wikipedia)。
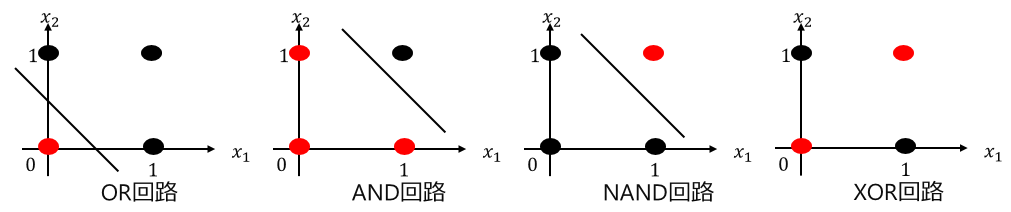
従って以下の図のように赤丸と黒丸を直線で分けることが出来るOR/AND/NAND回路は線形分離可能問題であり、XOR回路は直線で分けることが出来ないため線形分離不可能問題となります。
限界突破
XOR回路は単純パーセプトロンで解くことが出来ない問題と判明してしまいましたが、単純パーセプトロンとは関係なくXOR回路はOR/AND/NAND回路で作ることが出来ますね!
ということは、単純パーセプトロンで学習したOR/AND/NAND回路を連結させればXOR回路が作れるんじゃないか?ということが考え付きます。
物は試しということで、実際にやってみましょう。
以下の図のように各回路を連結させていきます。
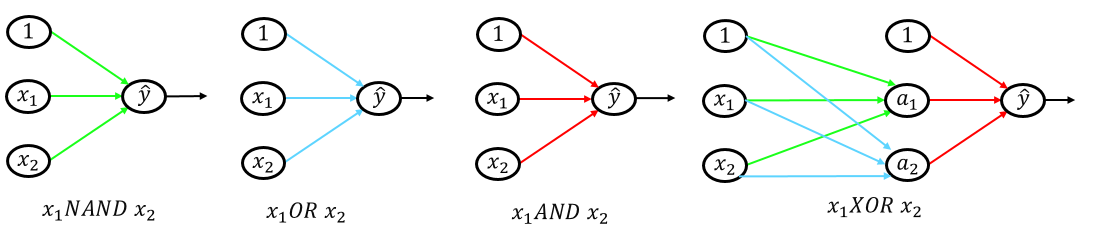
ここで用語の説明を。
一番最初の層($x_1,x_2$がある層)を入力層、最後の層($\hat{y}$がある層)を出力層、その二つの層に挟まれている層を全て中間層または隠れ層といいます。
上図において、XOR回路の$a_1, a_2$の層が中間層または隠れ層となります。
既に先ほど学習済みのOR/AND/NAND回路の単純パーセプトロンを使ってXOR回路を作ってみます。
実装
既に学習済みの各回路はそれぞれ以下の名前で定義しています。
- OR回路:SP_OR
- AND回路:SP_AND
- NAND回路:SP_NAND
そしてXORという名前の関数を以下のように定義します。
連結の仕方は上図と同じです。
def XOR(X, SP_or, SP_and, SP_nand):
a1 = SP_nand.Forward(X)
a2 = SP_or.Forward(X)
# a1とa2を横につなげて、A(4×2の行列)とする
A = np.c_[a1, a2]
Yh = SP_and.Forward(A)
return Yh
そしてこの関数を以下の様に実行するとXOR回路が出来ていることがわかります。
XOR(X, SP_OR, SP_AND, SP_NAND)
# 以下が出力されます。
# array([[0.],
# [1.],
# [1.],
# [0.]])
考察と、その先の未来
上記で示したように、単純パーセプトロンを連結させることで単純パーセプトロンが解くことが出来ない線形分離不可能問題を解くことが出来ました。
では単純パーセプトロンを連結させて学習すれば問題なしでしょうか?
学習するために必要なものを列挙してみましょう
- 入力:これはわかっています。
- 期待する出力:これもわかっています。
- 推定した出力:計算結果なのでわかります。
- 中間層の期待する出力:わかりません。
今回のXOR回路の様に簡単なものは中間層の期待する出力がわかっているのですが、通常は不明なために学習が出来ません。そこを改善したものが多層パーセプトロンとなります。
次の記事では多層パーセプトロンについて記載しようと思います。
次の記事を投稿しました!