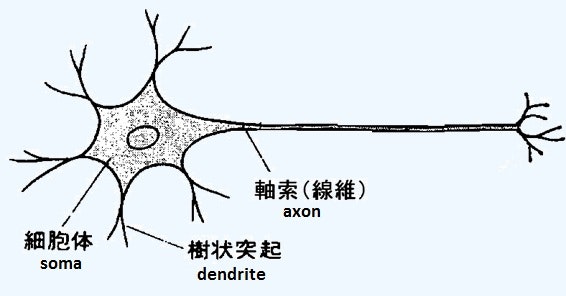
昨今流行りのDeep Learning(深層学習)ですが, ニューラルネットワークという分野に属しています。
今回はニューラルネットワークの基礎である単純パーセプトロンの理論を実装を交えつつ説明したいと思います。
ニューロンと形式ニューロン
1943年に神経生理学者・外科医であるウォーレン・マカロックと論理学者・数学者であるウォルター・ピッツがニューロンを基にした形式ニューロンを発表しました。(出典元:Wikipedia)
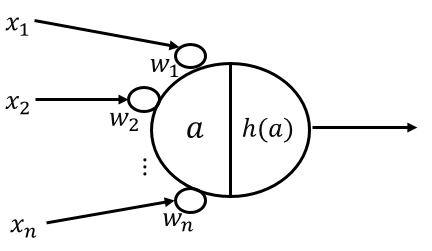
形式ニューロンは1つ以上の入力($x_j$)を持ち、各入力がそれぞれ重み($w_j$)に繋がっています。
この繋がっていますという記載ですが、数式的には$x_j × w_j$ということを示します。
次に各入力と重みの積を全て足し合わせ($a$)、それに対して活性化関数($h$)を出力とします。
活性化関数にはステップ関数が用いられ、$a$が閾値($\theta$)以上で1、閾値未満で0を出力します。
上記を数式で表すとそれぞれ以下となります。
$$ a = \sum_{ j=1 }^{ n } x_j w_j $$
h(a) = \left\{
\begin{array}{ll}
1 & (a \gt \theta) \\
0 & (a \leq \theta)
\end{array}
\right.
ここで、形式ニューロンによるAND回路を考えてみます。
AND回路とは入力が2つ、出力が1つの回路です。
出力する値は入力がともに1の時に1、
それ以外が入力されたら0を出力する回路となります。
- 重み:$w_1 = 1, w_2 = 1$
- 閾値:$\theta = 1.5$
重みと閾値の値が上記の場合、表の通りAND回路として正しく動作することがわかります。
$i$は入力データの番号です。
$i=3$の時の入力は$x_1 = 1, x_2 = 0$となります。
| i | $x_{j=1}$ | $x_{j=2}$ | $a$ | $a - \theta$ | $h(a)$ | 期待する出力 |
|---|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | -1.5 | 0 | 0 |
| 2 | 0 | 1 | 1 | -0.5 | 0 | 0 |
| 3 | 1 | 0 | 1 | -0.5 | 0 | 0 |
| 4 | 1 | 1 | 2 | 0.5 | 1 | 1 |
重みと閾値を適切に決めればOR回路やNOT回路も作成可能です。
ただし、どうやって決めればよいでしょうか?
私たちが知っているのは入力と期待する出力だけです。
それらから学習を通じて重みと閾値を適切に決める方法を取り入れたのが単純パーセプトロンになります。
単純パーセプトロン
形式ニューロンと比較して以下差分があります。
- 実数が入力可能
- 実数が出力可能
- 重みと閾値を学習を通じて探索
この学習についてですが、先ほど例に挙げたAND回路を使って説明していきます。
さて、重みと閾値を探索していく方法ですが、まずは知っていることを列挙してみましょう。
- 入力:知っていますね。
- 適切な重み:もちろんわかりません。
- 適切な閾値: これももちろんわかりません。
- 推定した出力 : これは計算結果なのでわかります。
- 期待する出力 : 知っています。
列挙した項目を見ると方法はさておき、ゴールは見えたと思います。
そうですね、ゴールとしては推定した出力が期待する出力と完全に同じになれば良いですね!
しかし自分で書いていてなんですが、値が完全に一致することはほぼありえません。
ましてや計算機で計算させるためどうしても誤差は発生します。
なのでゴールとしては推定した出力と期待する出力が十分に近ければ良いということになります。
方針が定まったので次はどうやって重みと閾値を適切な値にしていくか考えたいのですが、適切な値とは何でしょうか?何をもって適切な値とするのでしょうか?
思い出して欲しいのですが、ゴールとしては重みと閾値を使って計算した結果(推定した出力)と期待する出力が十分に近いことでしたね。ということは、期待する出力を$y$とすると$h(a) - y=-2$の時と、$h(a) - y=1$の時では、$h(a) - y=1$の時の重みと閾値の方が適切な値ということになりますね。
従って、$h(a) - y$が0に近づいていくように重みと閾値を更新していけばよいことになります。
ここで一旦数式を整理します。
まず、入力$x$ですがAND回路ですので上記表の通り$4×2$の行列となります。
\boldsymbol{X} =
\begin{pmatrix}
x_{11} & x_{12} \\
x_{21} & x_{22} \\
x_{31} & x_{32} \\
x_{41} & x_{42}
\end{pmatrix}
=
\begin{pmatrix}
0 & 0 \\
0 & 1 \\
1 & 0 \\
1 & 1
\end{pmatrix}
次は重みです。
重みは入力と繋がるため、入力と同じ数必要になります。
と書くと次元数は$4×2$と思うかもしれませんが、不正解です。
入力$4×2$は2次元ベクトルが4セットあるということですので、
正解は以下の通り$1×2$となります。
$$
\boldsymbol{W} = \
\begin{pmatrix}
w_{11} & w_{12}
\end{pmatrix}
$$
次に活性化関数と閾値ですが、実装を簡単にするためにバイアス項を導入します。
まず、常に入力が1となる入力($x_{i0}$)を導入します。
$x_{i0}$は入力のため、対応する重みが必要です。
それを$w_{10}$とすると、活性化関数の出力は以下となります。
h(a_i) = \left\{
\begin{array}{ll}
1 & (\sum_{j=1}^{2}(x_{ij} w_{1j}) + x_{i0} w_{10} \gt \theta) \\
0 & (\sum_{j=1}^{2}(x_{ij} w_{1j}) + x_{i0} w_{10} \leq \theta)
\end{array}
\right.
ここで$\theta = - x_{i0} w_{10} = -w_{10} = -b$とすると
h(a_i) = \left\{
\begin{array}{ll}
1 & ( \sum_{j=1}^{2}(x_{ij} w_{1j}) + b \gt 0) \\
0 & ( \sum_{j=1}^{2}(x_{ij} w_{1j}) + b \leq 0)
\end{array}
\right.
となり、$b$をバイアス項と呼びます。
そのままの流れで推定した出力$\boldsymbol{\hat{Y}}$も記載します。
\boldsymbol{\hat{Y}} =
\begin{pmatrix}
\hat{y_{1}} \\
\hat{y_{2}} \\
\hat{y_{3}} \\
\hat{y_{4}}
\end{pmatrix}
=
\begin{pmatrix}
h(a_{1}) \\
h(a_{2}) \\
h(a_{3}) \\
h(a_{4})
\end{pmatrix}
=
\begin{pmatrix}
h(\sum_{j=1}^{2} x_{1j}w_{1j} + b) \\
h(\sum_{j=1}^{2} x_{2j}w_{2j} + b) \\
h(\sum_{j=1}^{2} x_{3j}w_{3j} + b) \\
h(\sum_{j=1}^{2} x_{4j}w_{4j} + b)
\end{pmatrix}
= \boldsymbol{X}\boldsymbol{W}^T + b
ここでようやく、学習について考えていきます。
先ほども記載したとおり、推定した出力が期待する出力に近づくように重みを更新していけば良いのですが、どうやって計算していけばよいでしょうか?
ここで登場するのが勾配法です。
詳細な説明はwikiを見ていただくとして、ざっくり説明していきます。
勾配法
勾配降下法とも言われますが、最小化したい関数を微分して傾きが0となる点を探索する手法です。
なお、微分不可能点はどうするのという疑問があると思いますが、その場合は劣微分を考えるようです。
Preferred Networks Research Blogにて説明されていますので気になる人は確認してみてください。
勾配法は以下のステップで変数$x$を更新していきます。
- 探索したい変数を初期化する
- 最小化したい関数$f(x)$の微分$f^{\prime}(x)$を計算する
- $x$を以下の式で更新する
$x := x - \alpha f^{\prime}(x)$
$(0 < \alpha \leq 1)$ - 2.~3.を規定回数または$f^{\prime}(x)$が十分小さくなるまで繰り返します。
具体的に解いていきましょう。
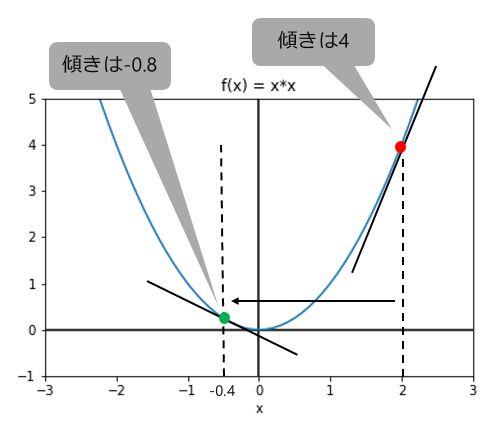
最小化したい関数を$f(x)=x^2$とします。
$x$の初期値を$x=2$とすると、傾きは$f^{\prime}(x)=2x=4$となります。
$\alpha = 0.6$とすると更新後の$x$は $x := 2 - 0.6 × 4 = -0.4$ 、
傾きは$f^{\prime}(x)=2×(-0.4)=-0.8$となります。
以下の図で分かる通り、$x$を更新する度に徐々に傾きが0に近づいていることがわかります。
このように微分を使用して$x$を探索していきます。
先ほどの例では最小化したい関数は$f(x)=x^2$でしたが、今回解きたいAND回路における最小化したい関数は何でしょうか?
そうです、推定した出力と期待する出力の差が最小化したい関数となります。
それを$J$とすると以下となります。
\begin{align}
J &= \frac{1}{2} \sum_{i=1}^{4}(\hat{y_i} - y_i)^2 \\
&= \frac{1}{2} \sum_{i=1}^{4}( h(\sum_{j=1}^{2}x_{ij}w_{1j} + b) - y_i)^2
\end{align}
ちなみに$J$のことを目的関数やコスト関数、誤差関数と言ったりします。
詳細はここを見てください。
$J$は二乗の形になっていますが、絶対値でも良いのではないか?という疑問を持つ方がいるかもしれません。
絶対値では0となる点で微分不可能となってしまうので、あまり宜しくありません(劣微分を考えればよいのかもしれませんが・・・)。
また、2で割っていますが微分時に出る$2$を打ち消すために付けています。
無くても問題ありませんが計算しやすくするためです。
上記式を見てわかる通り、更新する変数が$w_{11}, w_{12}, b$の3つあります。
そのため、以下の式の通り偏微分を使用して更新することになります。
w_{1j} := w_{1j} - \alpha \frac{\partial J}{\partial w_{1j}} \\
b := b - \alpha \frac{\partial J}{\partial b} \\
\frac{\partial J}{\partial w_{1j}} = \sum_{i=1}^{4}(\hat{y}_i - y_i)h\prime(a_i)x_{ij} \\
\frac{\partial J}{\partial b} = \sum_{i=1}^{4}(\hat{y}_i - y_i)h\prime(a_i)
なぜ上記となるのか理解できない方は末尾に記載した補足を参照してください。
変数を更新するために、すべての入力データを使う勾配法が最急降下法です。
なお、変数の更新は一斉にする必要があるので気を付けてください。
活性化関数
先ほどの式に置いて$h\prime$が出てきていますが、これは活性化関数の微分を表しています。
今まで活性化関数はステップ関数を使ってきましたが、これは微分不可能点があり、微分可能点においても微分の値が0となるため使用できません。
そこでステップ関数に形が似ているシグモイド関数を使うことにします。
シグモイド関数を表す数式は以下の通りです。
h(x) = \frac{1}{1+e^{-x}}
ステップ関数とシグモイド関数は以下の図の通りです。
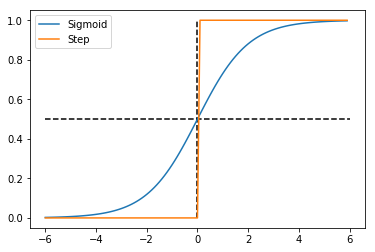
シグモイド関数は、$x$の値が$-\infty$に近づくほど$y$の値は$0$に、$x$の値が$+\infty$に近づくほど$y$の値は$1$に近づきます。
シグモイド関数の微分がわからない方はここを参照してください。
実装
では、いよいよ実装していきましょう。
今回はPythonで実装することにします。
Pythonのインストールは自力でお願いします。
WindowsやMac、LinuxユーザーでPython開発環境がない方はAnacondaをインストールするのが一番簡単だと思います。
FreeBSDユーザーはAnaconda入れられないので、すみません。
もう数年触っていないけど、いつかFreeBSDに関する記事書きたいな...
ライブラリ
必要なライブラリの設定です。
今回はJupyter Notebook上で実行するため、matplotplibの設定が必要となります。
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
定数の定義
次に入力と期待する出力を定義します。
$\boldsymbol{X}$は$4×2$の行列、$\boldsymbol{Y}$は$4×1$の行列となります。
それぞれの値については上の方に書いた表を参照してください。
X = np.array([[0,0],[0,1],[1,0],[1,1]])
Y = np.array([[0],[0],[0],[1]])
実装方針
単純パーセプトロンの機能を持つクラスを作ることにします。
メンバ変数として重みとバイアスを持ち、$\boldsymbol{X}$と$\boldsymbol{Y}$を入力すると重みとバイアスの適切な値を求めてくれるような関数を持ちます。
作る必要がある関数は以下となります。
- Forward:推定する出力を計算
- ActivationFunction:活性化関数を計算
- ActivationFunction_d:活性化関数の微分を計算
- J:推定する出力と期待する出力の誤差を計算
- Delta:重みとバイアス項の更新量を計算
- Fit:学習開始
Forward
推定する出力の計算ですが、必要な引数は入力$\boldsymbol{X}$だけです。
今考えると$\boldsymbol{X}$をメンバ変数にして引数省略しても良かったかも。
def Forward(self, X):
# 活性化関数への入力を計算しZに代入
Z = X.dot(self.W) + self.b
a = self.ActivationFunction(Z)
if not self.isRegression:
# 0.5以上の項は1.0に、0.5未満の項は0.0にする
return np.where(a > 0.5, 1.0, 0.0)
else:
return a
ActivationFunction
ActivationFunction()からSigmoid()を呼んでいます。
将来的に複数の活性化関数を実装しようかなと思っていたのですが、結局シグモイド関数だけしか実装しませんでした...
def Sigmoid(self, value):
return 1.0/(1.0 + np.exp(- value))
def ActivationFunction(self, value):
return self.Sigmoid(value)
ActivationFunction_d
こちらも同様にActivationFunction_d()からSigmoid_d()を呼んでいます。
def Sigmoid_d(self, value):
return self.Sigmoid(value) * (1.0 - self.Sigmoid(value))
def ActivationFunction_d(self, value):
return self.Sigmoid_d(value)
J
Forward()と同様、$\boldsymbol{Y}$をメンバ変数にして引数省略してもよかったですね。
def J(self, Yh, Y):
# コスト関数を計算しjに代入
j = ((Yh - Y) * (Yh - Y)).sum() / 2.0
return j
Delta
重みとバイアス項の更新量を計算しています。
def Delta(self, X, Y):
m, n = X.shape
# dw(n×1の行列)を0で初期化
dw = np.zeros((n,1))
db = np.zeros((1,1))
Z = X.dot(self.W) + self.b
Yh = self.ActivationFunction(Z)
G = self.ActivationFunction_d(Z)
for i in range(m):
# バイアス項の偏微分を計算
db[0][0] = db[0][0] + (Yh[i] - Y[i]) * G[i]
for j in range(n):
# 重みを計算しdw[j][0]に足し合わせる
dw[j][0] = dw[j][0] + (Yh[i] - Y[i]) * G[i] * X[i][j]
return dw, db
Fit
この関数を呼ぶことで学習が始まります。
def Fit(self, X, Y):
# 重みとバイアス項の初期化
self.W = np.random.rand(X.shape[1], 1)
self.b = np.zeros((1,1))
# コスト関数の値がどう変わったのかを保存するリストを初期化
J_List = []
# 重み更新ループ
for t in range(self.times):
Yh = self.ActivationFunction(X.dot(self.W) + self.b)
# 誤差の計算
j = self.J(Yh, Y)
J_List.append(j)
# 誤差がepsilon以下なら終了
if j <= self.epsilon:
break
# 重みとバイアス項の更新
dw, db = self.Delta(X, Y)
self.W = self.W - self.alpha * dw
self.b = self.b - self.alpha * db
return J_List
実行
ソース一式はGithubに置いておきました。
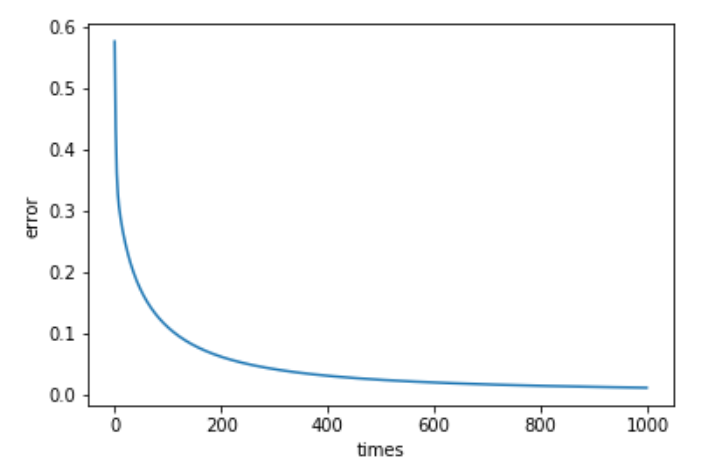
で、実際に実行してみた結果が以下です。
# AND回路の作成
SP = SimplePerceptron()
l = SP.Fit(X, Y)
# コスト関数が小さくなっていることの確認
plt.plot(l)
plt.xlabel("times")
plt.ylabel("error")
徐々に誤差が小さくなっていることがグラフからもわかります。
よって重みとバイアス項が適切な値に近づいているということになります。
まとめ
今回は単純パーセプトロンの理論と実装を記載してみました。
ライブラリを使うだけであれば、理論を理解していなくても良いのですが、パラメーターを弄ったりする場合は理解しておいた方が良いので、この記事が理解のはじめの一歩になれば幸いです。
誤字脱字、勘違いなどあればご指摘いただけると幸いです。
補足
$\hat{y}_i - y_i = u_i$とすると
\begin{align}
J &= \frac{1}{2} \sum_{i=1}^{4}(\hat{y_i} - y_i)^2 \\
&= \frac{1}{2} \sum_{i=1}^{4}(u_i)^2
\end{align}
となるので、合成関数の微分より
$$
\frac{\partial J}{\partial w_{1j}} = \frac{\partial J}{\partial u_i} \frac{\partial u_i}{\partial w_{1j}} \tag{1}
$$
となるので、$u_i$による$J$の偏微分と、$w_{1j}$による$u_i$の偏微分を計算すればよいことがわかります。
早速計算してみましょう。
\begin{align}
\frac{\partial J}{\partial u_{i}} &= \frac{1}{2} \frac{\partial \sum_{i=1}^{4}u_i^2}{\partial u_i} \\
&= \sum_{i=1}^{4}u_i \tag{2}
\end{align}
\begin{align}
\frac{\partial u_i}{\partial w_{1j}} &= \frac{\partial (\hat{y}_i - y_i)}{\partial w_{1j}} \\
&= \frac{\partial (h(a_i) - y_i)}{\partial w_{1j}} \\
&= \frac{\partial h(a_i)}{\partial w_{1j}} - \frac{\partial y_i}{\partial w_{1j}} \\
&= \frac{\partial h(a_i)}{\partial w_{1j}} \tag{3}
\end{align}
$y_i$は定数のため、微分すると0になるので消えています。
更に式(3)も合成関数の微分より、
\begin{align}
\frac{\partial h(a_i)}{\partial w_{1j}} &= \frac{\partial h(a_i)}{\partial a_i} \frac{\partial a_i}{\partial w_{1j}} \\
&= h\prime(a_i) x_{ij} \tag{4}
\end{align}
となります。
式(1)に式(2)(3)(4)を代入するとようやく計算終了となります。
\begin{align}
\frac{\partial J}{\partial w_{1j}} &= \frac{\partial J}{\partial u_i} \frac{\partial u_i}{\partial w_{1j}} \\
&= \frac{\partial J}{\partial u_i} \frac{\partial h(a_i)}{\partial a_i} \frac{\partial a_i}{\partial w_{1j}} \\
&= \sum_{i=1}^{4}u_i h\prime(a_i) x_{ij} \\
&= \sum_{i=1}^{4}(\hat{y}_i - y_i) h\prime(a_i) x_{ij}
\end{align}
同様にして、$\frac{\partial J}{\partial b}$も解くことが出来ますので、トライしてみてください。