前回の単純パーセプトロンの限界にて、単純パーセプトロン単体で解くことが出来ない線形分離不可能問題も、学習後の単純パーセプトロンを連結させることで解けることを確認しました。
今回の記事では学習していない単純パーセプトロンを連結させた状態で学習させる方法を確認し、そのまま誤差逆伝播方まで導出してみます。
単純パーセプトロンと多層パーセプトロン
単純パーセプトロンとは入力層と出力層のみから構成されるニューラルネットワークで、線形分離可能問題しか解くことが出来ませんでした。そこで登場したのが多層パーセプトロンでしたね。
多層パーセプトロンとは入力層と出力層の間に中間層(隠れ層)が存在するニューラルネットワークで、線形分離不可能問題も解くことが可能でしたが、中間層の重みとバイアス項を学習する方法がわかりませんでした。
そこで今回は基本に立ち返って考えてみましょう。
単純パーセプトロンで勾配法を使用することで、重みとバイアス項を学習していきましたが、学習するためには以下の情報が必要でしたね。
- 入力:$x$
- 期待する値:$y$
- 推定した値(予測値):$\hat{y}$
では、学習するために必要な情報は全て揃っているはずなのに、なぜ多層パーセプトロンでは学習が出来ないのでしょうか?
それは、中間層での期待する値がわからないからです。
期待する中間層での値がわからないために勾配法が使えず、結果として値を更新できないということになります。
ここで思い出してほしいのですが、$\hat{y}$には各層の重みとバイアス項が入っています。
ということは、目的関数$J$を、各層の重みとバイアス項で偏微分出来るはずです。
実際にやってみましょう。
力技での導出
想定するネットワーク
今回想定するネットワークは以下の図の通り、中間層が2つとなるネットワークです。
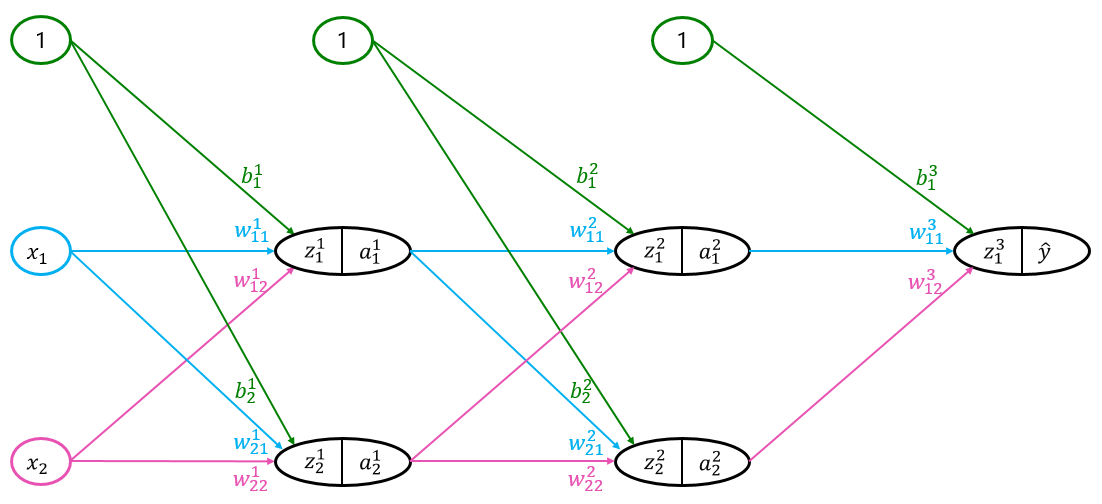
また、変数・関数の定義をしておきます。
- $l$:層を示す番号(入力層:$0$、出力層:$L$)
- $N^l$:$l$層のニューロン数
- $M$:入力データセットの数
- $w_{ij}^{l}$:$l-1$層の$j$番目のニューロンが$l$層の$i$番目のニューロンに接続している重み
- $b_{i}^{l}$:$l$層の$i$番目のニューロンに接続しているバイアス項
- $h$:活性化関数
- $z_i^l$:$l$層の$i$番目のニューロンに対する総入力
- $a_i^l$:$l$層の$i$番目のニューロンの出力
- $y_m$:m番目のデータセットを入力した際の期待する値
- $\hat{y_m}$:m番目のデータセットを入力した際の推定した値
- $J$:目的関数
順伝播
入力層から出力層に向かって$z$や$a$を計算することを順伝播といいます。
では、第1層から順に計算していきましょう。
第1層
\begin{align}
z_1^1 &= x_1w_{11}^1 + x_2w_{12}^1 + b_1^1 \\
z_2^1 &= x_1w_{21}^1 + x_2w_{22}^1 + b_2^1 \\
a_1^1 &= h(z_1^1) \\
a_2^1 &= h(z_2^1)
\end{align}
第2層
\begin{align}
z_1^2 &= a_1^1 w_{11}^2 + a_2^1 w_{12}^2 + b_1^2 \\
z_2^2 &= a_1^1 w_{21}^2 + a_2^1 w_{22}^2 + b_2^2 \\
a_1^2 &= h(z_1^2) \\
a_2^2 &= h(z_2^2)
\end{align}
第3層(出力層)
\begin{align}
z_1^3 &= a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3 \\
\hat{y} &= h(z_1^3)
\end{align}
目的関数
さてさて、ようやく$\hat{y}$まで求められましたので、目的関数を定義しましょう。
目的関数は従来同様、以下となります。
$$
J=\frac{1}{2}\sum_{m=1}^{M}(\hat{y_m} - y_m)^2
$$
式では、データセット毎に推定した値と期待する値の差を二乗して足し合わせています。
この値が小さくなればなるほど、推定した値が期待する値に近づいたということになります。
第3層(出力層)の重みとバイアス項の更新量
では実際に$J$を偏微分することで求めていきます。
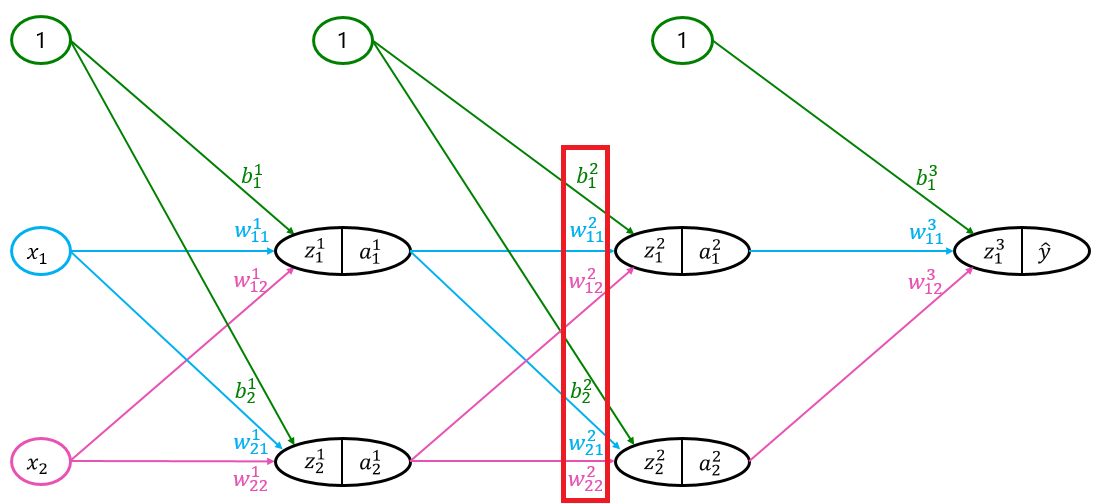
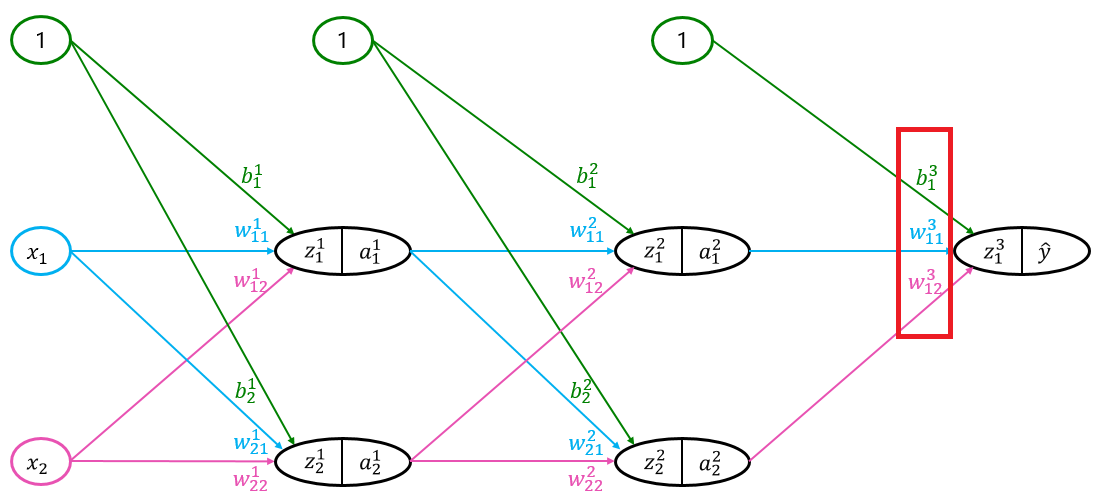
今回は第3層の重みとバイアス項の更新量を求めるので、以下の図において赤枠で囲った部分の偏微分をすることになります。
$u = \hat{y_m} - y_m$とすると
$$
J = \frac{1}{2}\sum_{m=1}^M{u^2}
$$
となります。
合成関数の微分より、
\begin{align}
\frac{\partial J}{\partial b_1^3} &= \frac{\partial J}{\partial u} \frac{\partial u}{\partial b_1^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial (\hat{y_m} - y_m)}{\partial b_1^3} \\
& y_m \text{は定数より} \\
& = \frac{\partial J}{\partial u} \frac{\partial \hat{y_m}}{\partial b_1^3} \\
& \hat{y_m}=h(z_1^3) \text{のため、合成関数の微分より} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3} {\partial b_1^3} \tag{1}
\end{align}
同様の解法で$w_{11}^3, w_{12}^3$も解くことが出来ます。
$b_1^3, w_{11}^3, w_{12}^3$での偏微分は以下となります。
\begin{align}
\frac{\partial J}{\partial b_1^3} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \\
\frac{\partial J}{\partial w_{11}^3} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial w_{11}^3} \\
\frac{\partial J}{\partial w_{12}^3} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial w_{12}^3}
\end{align}
第2層の重みとバイアスの更新量
$b_1^2$での偏微分の計算は出力層での解法と同じです。
ただ、合成関数がいっぱい出てきて、挫折しそうになりますが、頑張って解きましょう。
\begin{align}
\frac{\partial J}{\partial b_1^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial}{\partial b_1^2}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& b_1^2 \text{は} a_1^2 \text{に含まれるので} \\
&= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3\frac{\partial a_1^2}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3\frac{\partial h(z_1^2)}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial b_1^2} \tag{2}
\end{align}
$w_{11}^2, w_{12}^2, b_2^2, w_{21}^2, w_{22}^2$での偏微分も同様に解くことができ、第2層の重みとバイアス項の偏微分を纏めると以下となります。
\begin{align}
\frac{\partial J}{\partial b_{1}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial b_1^2} \\
\frac{\partial J}{\partial w_{11}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial w_{11}^2} \\
\frac{\partial J}{\partial w_{12}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial w_{12}^2} \\
\frac{\partial J}{\partial b_{2}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial z_2^2}{\partial b_2^2} \\
\frac{\partial J}{\partial w_{21}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial z_2^2}{\partial w_{21}^2}\\
\frac{\partial J}{\partial w_{22}^2} &= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial z_2^2}{\partial w_{22}^2}\\
\end{align}
第1層の重みとバイアスの更新量
ようやく第1層までたどり着きました。
あと少しなので頑張っていきましょう。
第1層の重みとバイアス項の偏微分ですが、他の層と解き方は同じです。
そのため式変形はかなり省略していますので、あしからず。
ではさっそく以下の赤枠で囲った部分の変数で偏微分していきます。
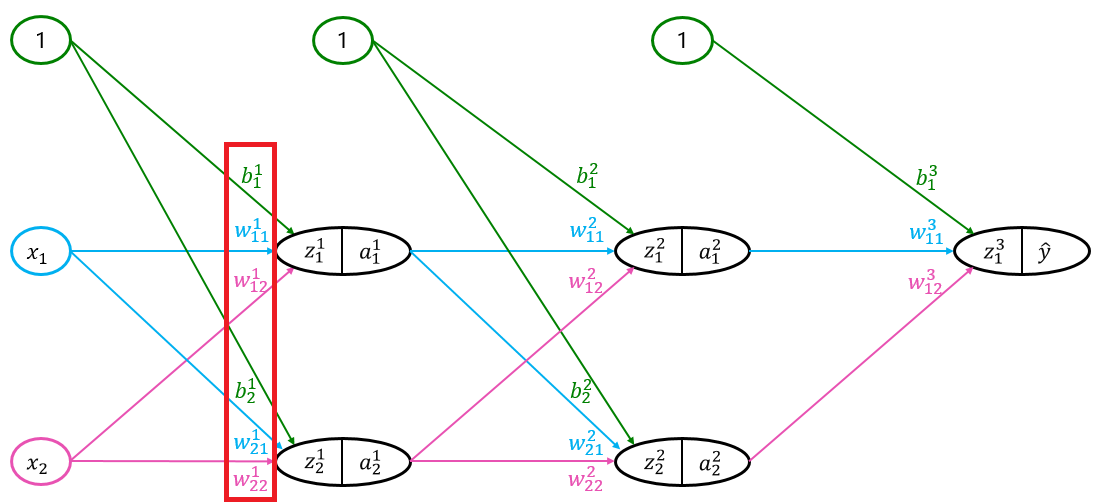
$b_1^1$での偏微分は、
\begin{align}
\frac{\partial J}{\partial b_1^1} & = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial}{\partial b_1^1}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& b_1^1 \text{は} a_1^2, a_2^2 \text{に含まれるため} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial a_1^2}{\partial b_1^1} + w_{12}^3 \frac{\partial a_2^2}{\partial b_1^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial }{\partial b_1^1}(a_1^1 w_{11}^2 + a_2^1 w_{12}^2 + b_1^2) + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial }{\partial b_1^1}(a_1^1 w_{21}^2 + a_2^1 w_{22}^2 + b_2^2) ) \\
& b_1^1 \text{は} a_1^1 \text{に含まれるため} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 \frac{\partial a_1^1 }{\partial b_1^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 \frac{\partial a_1^1}{\partial b_1^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 \frac{\partial h(z_1^1) }{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 \frac{\partial h(z_1^1)}{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 ) \frac{\partial h(z_1^1) }{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \tag{3}
\end{align}
となります!!
疲れた…
残りの偏微分ですが、今解いてきた方法で解けますので、皆さんで解いてみてください。
誤差逆伝播法の導出
式の変形
今まで長々と偏微分と合成関数の嵐を乗り切ってきましたが、ここで少し考え方を変えます。
まず、式(1)を改めてみてみます。
$$
\frac{\partial J}{\partial b_1^3} = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \tag{1}
$$
右辺の第3項は$z_1^3$を$b_1^3$で偏微分していますが、よく考えれば$J$には$z_1^3$が含まれるので以下の様に変形することが出来るはずです。
$$
\frac{\partial J}{\partial b_1^3} = \frac{\partial J}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3}
$$
実際に解いてみましょう。
\begin{align}
\frac{\partial J}{\partial b_1^3} &= \frac{\partial J}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial \hat{y_m}}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial b_1^3} \tag{1'}
\end{align}
式(1)と(1')が等価であることが示せました。
同様に、式(2)をみてみましょう。
$$
\frac{\partial J}{\partial b_1^2} = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial b_1^2} \tag{2}
$$
こちらも、右辺の第5項は$z_1^2$を$b_1^2$で偏微分していますが、$J$には$z_1^2$が含まれるので以下の様に変形することが出来るはずです。
\begin{align}
\frac{\partial J}{\partial b_1^2} & = \frac{\partial J}{\partial z_1^2} \frac{\partial h(z_1^2)}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^2} \frac{\partial h(z_1^2)}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial z_1^2} \frac{\partial h(z_1^2)}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial}{\partial z_1^2}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \frac{\partial h(z_1^2)}{\partial b_1^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial h(z_1^2)}{\partial b_1^2} \tag{2'}
\end{align}
こちらも式(2)と(2')が等価であることが示せました。
最後に式(3)も見てみましょう。
$$
\frac{\partial J}{\partial b_1^1}= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 ) \frac{\partial h(z_1^1) }{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \tag{3}
$$
こちらも、右辺の最終項は$z_1^1$を$b_1^1$で偏微分していますが、$J$には$z_1^1$が含まれるので以下の様に変形することが出来るはずです。
\begin{align}
\frac{\partial J}{\partial b_1^1} & = \frac{\partial J}{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial z_1^3}{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \\
&= \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \frac{\partial}{\partial z_1^1}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \frac{\partial z_1^1}{\partial b_1^1} \\
& a_1^2, a_2^2\text{に}z_1^1\text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} ( w_{11}^3 \frac{\partial a_1^2}{\partial z_1^1} + w_{12}^3 \frac{\partial a_2^2}{\partial z_1^1}) \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial z_1^2}{\partial z_1^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial z_2^2}{\partial z_1^1}) \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} \{ w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} \frac{\partial }{\partial z_1^1}(a_1^1 w_{11}^2 + a_2^1 w_{12}^2 + b_1^2 ) + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} \frac{\partial }{\partial z_1^1}(a_1^1 w_{21}^2 + a_2^1 w_{22}^2 + b_2^2)\} \frac{\partial z_1^1}{\partial b_1^1} \\
& a_1^1 \text{のみ} z_1^1 \text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 \frac{\partial a_1^1}{\partial z_1^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 \frac{\partial a_1^1 }{\partial z_1^1} ) \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 \frac{\partial h(z_1^1)}{\partial z_1^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 \frac{\partial h(z_1^1) }{\partial z_1^1} ) \frac{\partial z_1^1}{\partial b_1^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_1^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_1^2} w_{11}^2 + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_2^2} w_{21}^2 ) \frac{\partial h(z_1^1) }{\partial z_1^1} \frac{\partial z_1^1}{\partial b_1^1} \tag{3'}
\end{align}
こちらも式(3)と(3')が等価であることが示せました。
従って、$J$を重みで偏微分した式は以下の式(4)で表せることが推察されます。(証明ではないことに注意!)
なお、記載簡略化のため、これ以後バイアス項は出力が常に$1$となる$l-1$層のニューロンから、$l$層のニューロンに接続する重み$w_{i0}^l$と考えます。
$$
\frac{\partial J}{\partial w_{ij}^l} = \frac{\partial J}{\partial z_{i}^l} \frac{\partial z_i^l}{\partial w_{ij}^l} \tag{4}
$$
式(4)において右辺の第2項は簡単に計算することが出来ますが、問題は第1項です。
そのため、第1項を$\delta$とおくことにします。
$$
\frac{\partial J}{\partial w_{ij}^l} = \delta_i^l \frac{\partial z_i^l}{\partial w_{ij}^l} \tag{4'}
$$
$$
\delta_i^l = \frac{\partial J}{\partial z_{i}^l} \tag{5}
$$
では、実際に$\delta$を出力層側から解いてみましょう。
出力層側からなので$l=3$で、ニューロンは1つしかないので$i=1$ですね。
\begin{align}
\delta_1^3 & = \frac{\partial J}{\partial z_{1}^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_{1}^3} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3}
\end{align}
次に第2層の1番目のニューロンについて解いてみます。
\begin{align}
\delta_1^2 & = \frac{\partial J}{\partial z_{1}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_{1}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial z_1^3}{\partial z_{1}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial }{\partial z_{1}^2}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& a_1^2 \text{のみ} z_1^2 \text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{11}^3 \frac{\partial a_1^2 }{\partial z_{1}^2} \\
& = \underline{ \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} } w_{11}^3 \frac{\partial h(z_1^2) }{\partial z_{1}^2} \\
\end{align}
上式において、下線部分は$\delta_1^3$であるため、以下に書き換えます。
\begin{align}
\delta_1^2 & = \delta_1^3 w_{11}^3 \frac{\partial h(z_1^2) }{\partial z_{1}^2} \\
\end{align}
本来多量に計算しなければならない$\delta$が、出力層側に近い層の$\delta$を使って簡単に表すことが出来ました。
同様に第2層の1番目のニューロンについても解いてみます。
\begin{align}
\delta_2^2 & = \frac{\partial J}{\partial z_{2}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_{2}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{2}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial z_1^3}{\partial z_{2}^2} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial }{\partial z_{2}^2}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& a_2^2 \text{のみ} z_2^2 \text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{12}^3 \frac{\partial a_2^2 }{\partial z_{2}^2} \\
& = \underline{ \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} } w_{12}^3 \frac{\partial h(z_2^2) }{\partial z_{2}^2} \\
\end{align}
こちらもやはり下線部に$\delta_1^3$が出てきていますので、
$$
\delta_2^2 = \delta_1^3 w_{12}^3 \frac{\partial h(z_2^2) }{\partial z_{2}^2}
$$
となります。
つづいて、第1層の1番目のニューロンについて解いてみましょう。
\begin{align}
\delta_1^1 & = \frac{\partial J}{\partial z_{1}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_{1}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial z_1^3}{\partial z_{1}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial }{\partial z_{1}^1}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& z_1^1 \text{は} a_1^2, a_2^2 \text{の両方に含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial a_1^2}{\partial z_{1}^1} + w_{12}^3 \frac{\partial a_2^2}{\partial z_{1}^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{1}^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} \frac{\partial z_1^2}{\partial z_{1}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} \frac{\partial z_2^2}{\partial z_{1}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \{ w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} \frac{\partial }{\partial z_{1}^1}(a_1^1 w_{11}^2 + a_2^1 w_{12}^2 + b_1^2) + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} \frac{\partial }{\partial z_{1}^1}(a_1^1 w_{21}^2 + a_2^1 w_{22}^2 + b_2^2) \} \\
& a_1^1 \text{のみ} z_1^1 \text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{11}^2 \frac{\partial a_1^1}{\partial z_{1}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{21}^2 \frac{\partial a_1^1 }{\partial z_{1}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{11}^2 \frac{\partial h(z_1^1)}{\partial z_{1}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{21}^2 \frac{\partial h(z_1^1) }{\partial z_{1}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{11}^2 \frac{\partial h(z_1^1)}{\partial z_{1}^1} + \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{21}^2 \frac{\partial h(z_1^1) }{\partial z_{1}^1} \\
& = \delta_1^2 w_{11}^2 \frac{\partial h(z_1^1)}{\partial z_{1}^1} + \delta_2^2 w_{21}^2 \frac{\partial h(z_1^1) }{\partial z_{1}^1} \\
& = \frac{\partial h(z_1^1) }{\partial z_{1}^1}(\delta_1^2 w_{11}^2 + \delta_2^2 w_{21}^2 ) \\
\end{align}
最後のニューロンである、第1層の2番目のニューロンについて解いてみます。
\begin{align}
\delta_2^1 & = \frac{\partial J}{\partial z_{2}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial u}{\partial z_{2}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{2}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial z_1^3}{\partial z_{2}^1} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \frac{\partial }{\partial z_{2}^1}(a_1^2 w_{11}^3 + a_2^2 w_{12}^3 + b_1^3) \\
& z_2^1 \text{は} a_1^2, a_2^2 \text{の両方に含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial a_1^2}{\partial z_{2}^1} + w_{12}^3 \frac{\partial a_2^2}{\partial z_{2}^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{2}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^1} ) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} (w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} \frac{\partial z_1^2}{\partial z_{2}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} \frac{\partial z_2^2}{\partial z_{2}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} \{ w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} \frac{\partial }{\partial z_{2}^1}(a_1^1 w_{11}^2 + a_2^1 w_{12}^2 + b_1^2) + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} \frac{\partial }{\partial z_{2}^1}(a_1^1 w_{21}^2 + a_2^1 w_{22}^2 + b_2^2) \} \\
& a_2^1 \text{のみ} z_2^1 \text{が含まれるため,} \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{12}^2 \frac{\partial a_2^1}{\partial z_{2}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{22}^2 \frac{\partial a_2^1 }{\partial z_{2}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} ( w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{12}^2 \frac{\partial h(z_2^1)}{\partial z_{2}^1} + w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{22}^2 \frac{\partial h(z_2^1) }{\partial z_{2}^1}) \\
& = \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{11}^3 \frac{\partial h(z_1^2)}{\partial z_{1}^2} w_{12}^2 \frac{\partial h(z_2^1)}{\partial z_{2}^1} + \frac{\partial J}{\partial u} \frac{\partial h(z_1^3)}{\partial z_{1}^3} w_{12}^3 \frac{\partial h(z_2^2)}{\partial z_{2}^2} w_{22}^2 \frac{\partial h(z_2^1) }{\partial z_{2}^1} \\
& = \delta_1^2 w_{12}^2 \frac{\partial h(z_2^1)}{\partial z_{2}^1} + \delta_2^2 w_{22}^2 \frac{\partial h(z_2^1) }{\partial z_{2}^1} \\
& = \frac{\partial h(z_2^1) }{\partial z_{2}^1}( \delta_1^2 w_{12}^2 + \delta_2^2 w_{22}^2) \\
\end{align}
以上のことから、出力層側の$\delta$さえ計算できていれば、$\delta$は簡単に求めることができます。
図で理解
今まで長々と全ての$\delta$計算してきましたが、図で確認してみましょう。
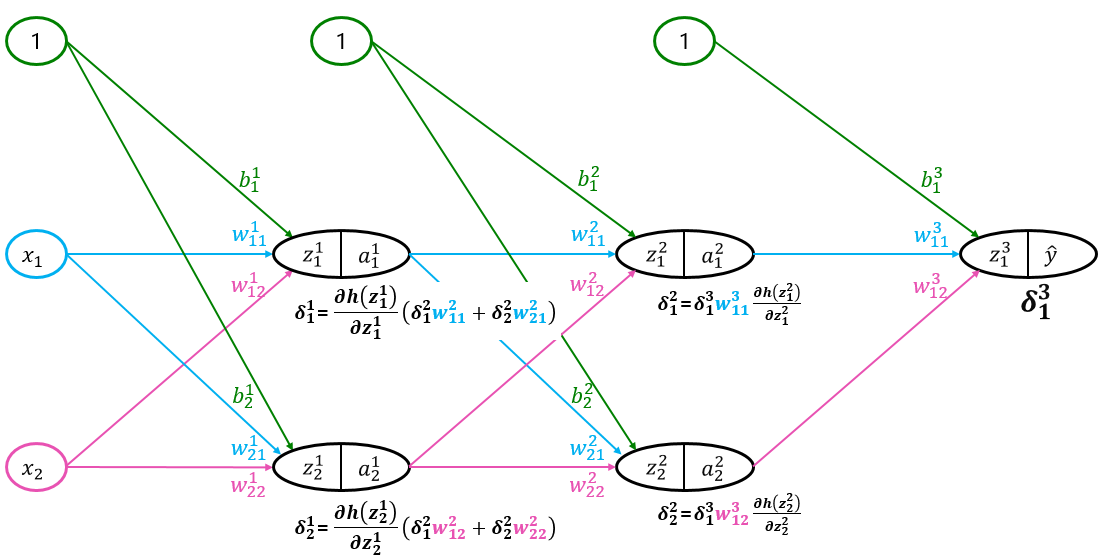
上記図には各$\delta$を記載しているのですが、見ると一目瞭然ですね。
$l$層$i$番目のニューロンの$\delta_i^l$は、そのニューロンからの出力を受け取る$l+1$層のニューロンの$\delta$かける重みの総和に、$l$層$i$番目のニューロンの出力を微分したものを掛け合わせたものですね。
式にすると以下となります。
$$
\delta_i^l = \frac{\partial h(z_i^l)}{\partial z_i^l} \sum_{j=1}^{N^{l+1}} \delta_j^{l+1} w_{ji}^{l+1}
$$
図や式からわかる通り、$\delta$は出力層側の$\delta$が含まれるため、出力層側の$\delta$さえ計算すれば、計算量が大幅に削減できることがわかります。
順伝播(推定した値を算出するため、入力層から出力層に向かって計算すること)と計算する方向が逆のため、$\delta$の計算を逆伝播といいます。
伝播するのは誤差(目的関数)なので、そこから誤差逆伝播法といいます。
やっと言えた...
まとめ
各重みの偏微分は以下の式で求めることが出来ます。
$$
\frac{\partial J}{\partial w_{ij}^l} = \delta_i^l \frac{\partial z_i^l}{\partial w_{ij}^l} \tag{4'}
$$
$$
\delta_i^l = \frac{\partial h(z_i^l)}{\partial z_i^l} \sum_{j=1}^{N^{l+1}} \delta_j^{l+1} w_{ji}^{l+1}
$$
終わりに
誤字脱字、記載誤りなどあればご指摘ください。
とくに添え字間違えは大いにありそうでびくびくしています。。。
なお、今回は数式のみですが、そのうちPythonで誤差逆伝播法を実装した記事でも書こうかなと思います。