はじめに
ロジスティック回帰をニューラルネットで実装したときの誤差逆伝播法の計算について、参考書では省かれていたので自力で数式を用いて解説及び実装してみます。
本記事の特徴は以下です。
- バッチ学習を考慮している
- 偏微分を真面目に計算した
なお、数学(行列や偏微分など)の解説や復習はしません。必要な方は 高校数学で理解・実装するニューラルネットワーク が詳しかったのでこれを参照してください。
ニューラルネットワークとは
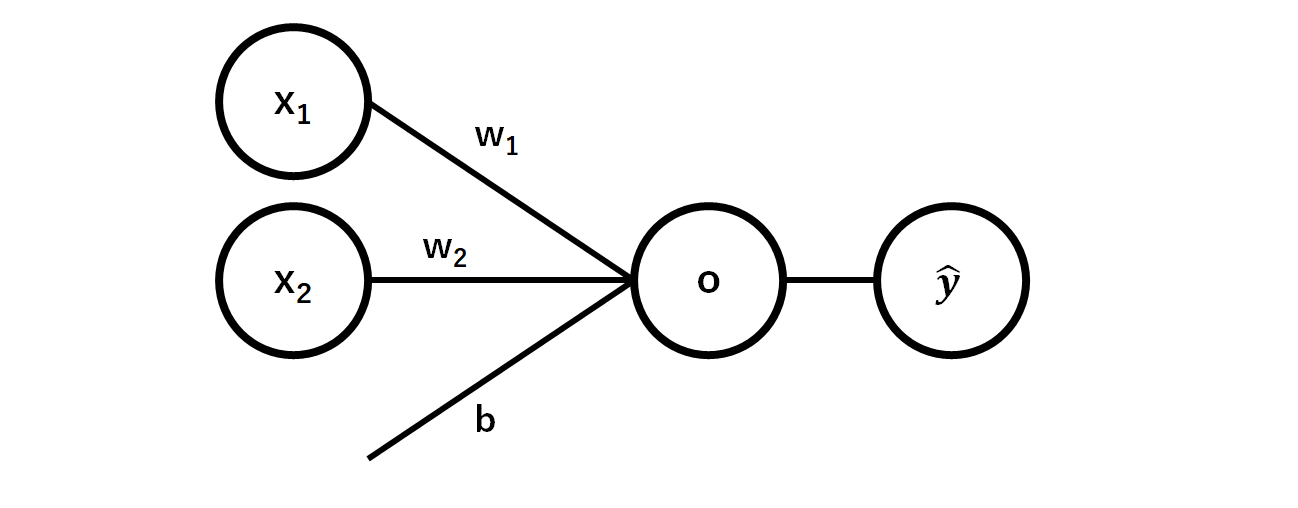
ニューラルネットワークの基本構造は以下の図のように複数の信号を入力($x$)として受け取り、それにある処理をして、出力するというものです。処理としては、重み($w$)をかけてバイアス($b$)を足すということを行います。
これを数式で書くと以下のようになります。
o=x_1w_1+x_2w_2+b
そして、出力$o$を活性化関数と呼ばれる非線形関数を用いて$\hat{y}$に変換することで、多層にしたときに複雑な関数を表現できるようにしています。
一般的な説明はここまでで、$x$をベクトルとして扱っていると思いますが、このままだとバッチ学習で実装できないので、行列を用いて深堀りしていきます。
まず、バッチ数を$N$(一つ一つの要素を$i$)、入力次元数を$M$(同じく$j$)、出力次元数(クラス数)を$K$(同じく$k$)と置きます。
このとき、上のニューラルネットワークで出てくる各変数の添え字は$x_{ij},w_{jk},o_{ik},\hat{y}_{ik}$のようになっており、上図に対応した図は以下のようにあらわされます。
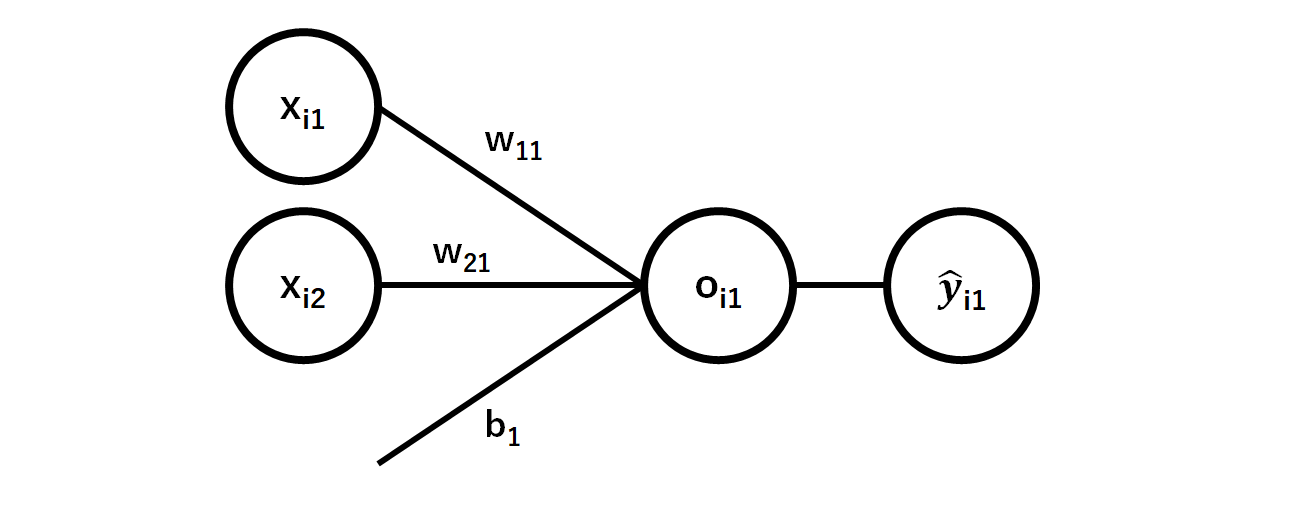
バッチ数$i$が一つの値しか現れていないのは、この図がN個あり(上に積み重なっていると思うとよいかも)それぞれが全く同じ構造になっているので省略しているからです。
ロジスティック回帰の構造
さて、ニューラルネットワークの簡単な例としてロジスティック回帰を考えてみます。ロジスティック回帰は2クラス分類ですが、$p$と$1-p$でそれぞれのクラスの確率を計算できるので、出力層は1層になります。
いま、各パラメーターを以下のように置きます。
- N: バッチ数 = 4
- M: 入力次元 = 2
- K: クラス(出力次元)数 = 1
具体的には例として以下のような値を考えています。なお、括弧の中の値は行列またはベクトルのサイズです。
入力:$x(N, M)$
x=\left(\begin{array}{cc}0 & 0\\0 & 1\\1 & 0\\1 & 1\end{array}\right)
正解:$y(N, K)$
y=\left(\begin{array}{cc}0\\0\\0\\1\end{array}\right)
重み:$w(M, K)$
w=\left(\begin{array}{c}0\\1\end{array}\right)
バイアス:$b(1, K)$
b=\left(\begin{array}{c}0\end{array}\right)
このとき、ニューロンの出力値$o(N, K)$は行列積を用いて、
o=xw+b
とあらわすことができます。(正確には$b$の1次元目はブロードキャストしてN次元にして計算している)
また、活性化関数としてシグモイドを考えると、予測値$\hat{y}(N, K)$は次のようになります。
\hat{y}_{ik}=\cfrac{1}{1+\exp{\left(-o_{ik}\right)}}
さらに、目的関数をクロスエントロピー誤差関数$E$とすると以下のようになります。
E=-\cfrac{1}{N}\sum_{i=1}^N\sum_{k=1}^K y_{ik}\log{\hat{y}_{ik}}
ただし、いま、ロジスティクス回帰なので次のように書き換えておきます。
E=-\cfrac{1}{N}\sum_{i=1}^N\left[y_{ik}\log{\hat{y}_{ik}}+(1-y_{ik})\log{(1-\hat{y}_{ik})}\right]\,(ただしk=1)
以上で、順伝播を数式で追うことができました。
逆伝播
ようやく本題の逆伝播ですが、そのためにはまず勾配を求める必要がありその定義は以下のように各パラメーターによる目的関数の偏微分です。これを追っていけるように連鎖律でばらしていきます。ただし、以下では煩雑になるのを防ぐため、 $k$を省略します。
\cfrac{\partial E}{\partial w_{j}}=\sum_{i=1}^{N}\cfrac{\partial o_{i}}{\partial w_{j}}\cfrac{\partial \hat{y}_{i}}{\partial o_{i}}\cfrac{\partial E}{\partial \hat{y}_{i}}\left(\because i\neq i'のとき\cfrac{\partial \hat{y}_{i}}{\partial o_{i'}}=0\right)
それぞれ考えると、第一項は
\cfrac{\partial o_i}{\partial w_j}=\cfrac{\partial}{\partial w_j}\left(\sum_{j=1}^Mx_{ij} w_{j}+b\right)=x_{ij}
第二項は
\cfrac{\partial \hat{y}_i}{\partial o_i}=\cfrac{\partial}{\partial o_i}\cfrac{1}{1+\exp{\left(-o_{i}\right)}}\\
=\cfrac{1}{(1+\exp{(-o_i)})^2}\exp{(-o_i)}\\
=\hat{y}_i^2\left(\cfrac{1}{\hat{y}_i}-1\right)
第三項は
\cfrac{\partial E}{\partial \hat{y}_i}=\cfrac{\partial}{\partial \hat{y}_i}\left(-\cfrac{1}{N}\sum_{i=1}^N\left[y_{i}\log{\hat{y}_{i}}+(1-y_{i})\log{(1-\hat{y}_{i})}\right]\right)\\
=-\cfrac{1}{N}\left(\cfrac{y_i}{\hat{y}_i}-\cfrac{1-y_i}{1-\hat{y}_i}\right)\\
=\cfrac{1}{N}\cfrac{\hat{y}_i-y_i}{\hat{y_i}(1-\hat{y}_i)}
よって、
\cfrac{\partial E}{\partial w_j}=\sum_{i=1}^{N}\left(x_{ij}\cdot \hat{y}_i^2\left(\cfrac{1}{\hat{y}_i}-1\right)\cdot \cfrac{1}{N}\cfrac{\hat{y}_i-y_i}{\hat{y}_i(1-\hat{y}_i)}\right)\\
=\cfrac{1}{N}\sum_{i=1}^Nx_{ij}(\hat{y}_i-y_i)
お疲れさまでした。これで重み$w$の勾配を求めることができました。
同様にして、バイアス$b$の勾配は
\cfrac{\partial E}{\partial b}=\cfrac{1}{N}\sum_{i=1}^N(\hat{y}_i-y_i)=\hat{y}_i-y_i
これらをもとに、学習率$\eta$を用いて以下のようにパラメーターを更新することができました。
w_j=w_j-\eta\cfrac{\partial E}{\partial w_j}\\
b=b-\eta\cfrac{\partial E}{\partial b}
pythonで実装
上記の議論をもとにpythonで実装してみます。なお、コードはcolab上にあげてあります。
データの準備
まず、x,y,w,bの値を用意します。
# 学習データ
x = np.array(([[0, 0],
[0, 1],
[1, 0],
[1, 1]]))
y = np.array([[0], [0], [0], [1]])
print(x.shape, y.shape) # (4, 2) (4, 1)
# 初期の重みをバイアス
w = np.array([[0], [1]]).astype('float32')
b = np.array([[0]]).astype('float32')
print(w.shape, b.shape) # (2, 1) (1, 1)
学習
学習は以下のようにfor文で実装します。
eta = 0.2 # 学習率
E_stock = [] # 目的関数の記録
for epoch in range(1000):
# 予測値を計算
y_hat = sigmoid(np.dot(x, w) + b)
E = - (y * np.log(y_hat) + (1 - y) * np.log(1 - y_hat)).sum() / N
E_stock.append(E)
# 逆伝搬
dw = (x * (y_hat - y)).sum(axis=0, keepdims=True) / N
db = (y_hat - y).sum(axis=0, keepdims=True) / N
# パラメーターの更新
w -= eta * dw.T
b -= eta * db.T
学習結果
x=\left(\begin{array}{cc}0 & 0\\0 & 1\\1 & 0\\1 & 1\end{array}\right)
の予測値は[0.00136398, 0.08900953, 0.08891836, 0.87471228]となり、正解の[0, 0, 0, 1]に近い結果が返ってきていることから学習できていることがわかります。
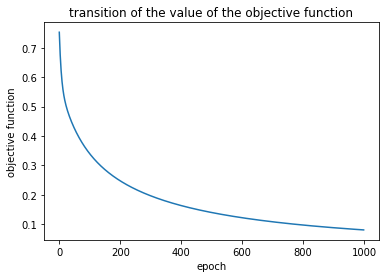
目的関数の値が減少しており、学習が進んでいることがうかがえます。
さらに、xの値を予測クラスを図示してみると下のようになりました。
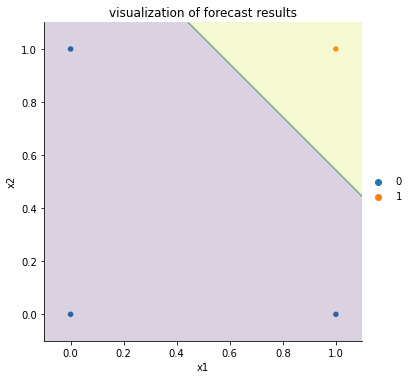
きちんと分離できていることがわかりました。
好評だったら多層のものやCNNなどほかのアーキテクチャでも計算してみたいと思います。