はじめに
この記事は高校レベルの数学の概念を用いてニューラルネットワークの仕組みを理解・実装まで解説するものです。細かな理論の説明はせずにforwardとbackwardの計算がどのように行われているかのみを実際に実装しながら確かめていきます(勾配法などの学習や最適化周りの説明はありません)。
実装にはPython+Numpyを使います。基本的にnumpyはimportされているものとしてコードを書きます。この記事は直感的な理解に重きを置いているので理論や定理に関して見当違いな表現をする場合もありますがご了承ください。また、一般化をしてしまうと添え字がごちゃごちゃしてわからなくなる場合もあるので基本的に具体例で理解をしていきます。
説明に使う数学について
ニューラルネットワークを理解・実装する上でベクトルの内積、行列積、幾つかの微分公式が必要になるので簡単に解説します。高校数学がしっかりと理解できている人は飛ばして構いません。
ベクトルの内積
以下の二つのベクトルを考えます。
\vec{x} = ({x_1, x_2, x_3}),\:\vec{w} = ({w_1, w_2, w_3})
このベクトル$\vec{x}$と$\vec{w}$の内積は以下で定義されます。
\vec{w}・\vec{x} = (w_1x_1+w_2x_2+w_3x_3)
話としては簡単で対応した要素ごとに掛け合わせて足し合わせるだけです。numpyを使って内積は以下のように書けます。
x = np.random.randn(3)
w = np.random.randn(3)
np.dot(w,x)
行列積
現在高校数学で行列は扱っていないようですが、行列を用いたほうが表記や実装が簡単になるので頑張って理解してください。とは言え必要なのは行列はベクトルを並べたものということと、その掛け算足し算はどのように行われるかさえ分かれば良いので我慢して覚えてみてください。以下の二つの行列を考えます。
X=\left(\begin{matrix}
x_{11} & x_{12} & x_{13} \\
x_{21} & x_{22} & x_{32}
\end{matrix}\right),\:
W=\left(\begin{matrix}
w_{11} & w_{12} \\
w_{21} & w_{22} \\
w_{31} & w_{32}
\end{matrix}\right)
この二つの行列$X$,$W$の掛け算は以下で定義されます。
WX = \left(\begin{matrix}
w_{11}x_{11}+w_{21}x_{12}+w_{31}x_{13} & w_{12}x_{11}+w_{22}x_{12}+w_{32}x_{13} \\
w_{11}x_{21}+w_{21}x_{22}+w_{31}x_{23} & w_{12}x_{21}+w_{22}x_{22}+w_{32}x_{23}
\end{matrix}\right)
少しややこしいですが、$X$の1行目{$x_{11}, x_{12}, x_{13}$}と$W$の1列目{$w_{11}, w_{21}, w_{31}$}のベクトルの内積が1行1列目に、$X$の2行目{$x_{21}, x_{22}, x_{23}$}と$W$の1列目のベクトルの内積が2行1列目にという感じに、前の行列のn行目と後ろの行列のm列目のベクトルの内積がn行m列目の値になります。注意として前の行列の行数と後ろの行列の列数が等しい場合にしか掛け算をすることはできません。
行列積をnumpyで表現すると以下のようになります。
X = np.random.randn(2,3)
W = np.random.randn(3,2)
np.dot(X,W)
また、行数と列数が一致していない場合はエラーが起こります。
X = np.random.randn(3,2)
W = np.random.randn(3,2)
np.dot(X,W) # エラー
X = np.random.randn(1,4)
W = np.random.randn(4,2)
np.dot(X, W) # 計算可能
微分公式
以下に今回使用する微分の公式を幾つか挙げておきます。
f(x)=x+4\:\:\:---->\:\:f'(x)=1\\
f(x)=1/x\:\:\:---->\:\:f'(x)=-1/x^2\\
f(x)=4x\:\:\:---->\:\:f'(x)=4\\
f(x)=\exp(x)\:\:---->\:\:f'(x)=\exp(x)
ニューラルネットワークとは
ややこしいことは置いておいてニューラルネットワークとは以下の図に示すようにある入力に対して重みと呼ばれる数値をかけてバイアスという数値を足し合わせることで特定の出力を表現するものになります。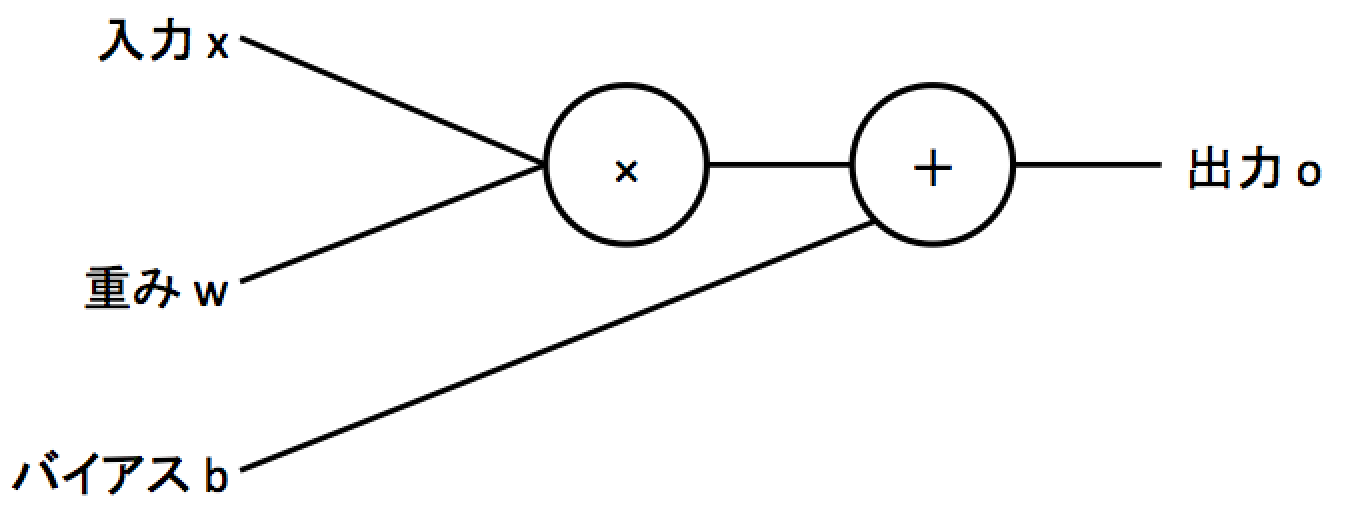
上の図を式にすると$o=wx + b$になります。中学数学で習う一次関数と同じ形で、一次関数のような関数を線形な関数といいます。実際のニューラルネットワークでは入力や出力は数百から数千になり、式でいうと$o=w_{1}x_{1}+w_{2}x_{2}+...+w_{n}x_{n}+b$のようになります。さらにニューラルネットワークはこの出力に対し非線形な関数(二次関数のような曲線の関数)を使う事で複雑な関数を表現していきます。
この重みとバイアスを、問題に合わせてニューラルネットワークが適切な出力を出すように学習していきます。具体的にどのようなことができるかはstanfordのconvnetjsを見るとわかると思います。一つ例としてconvnetjsのdemo: toy 2d classification with 2-layer neural networkを見ます。以下の図は2次元の緑のデータと赤のデータを分ける問題を解くために学習されたニューラルネットワークの学習結果になります。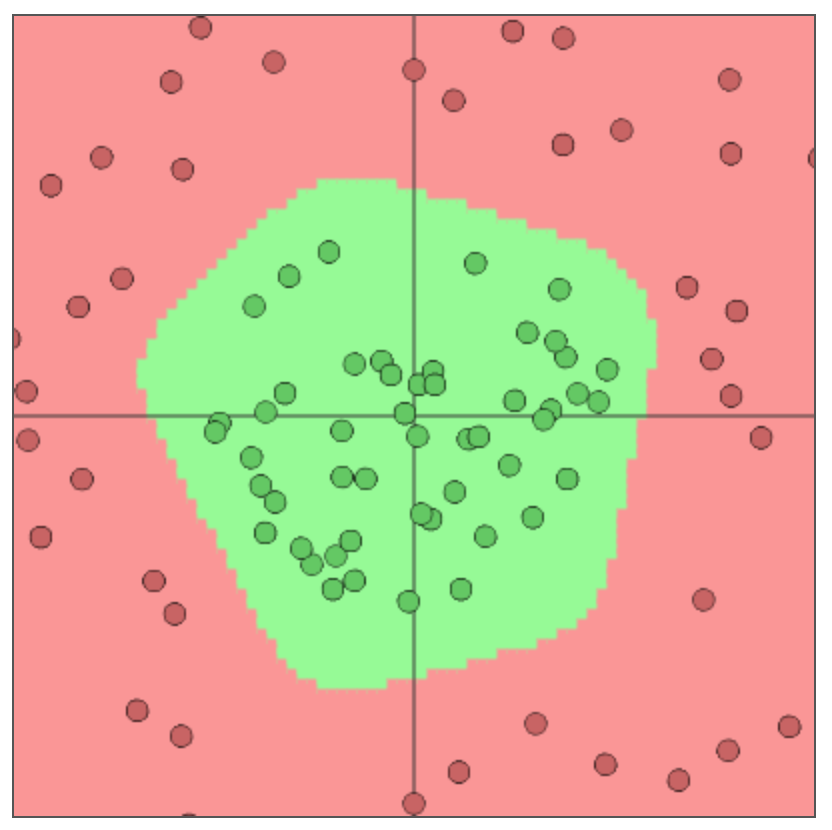
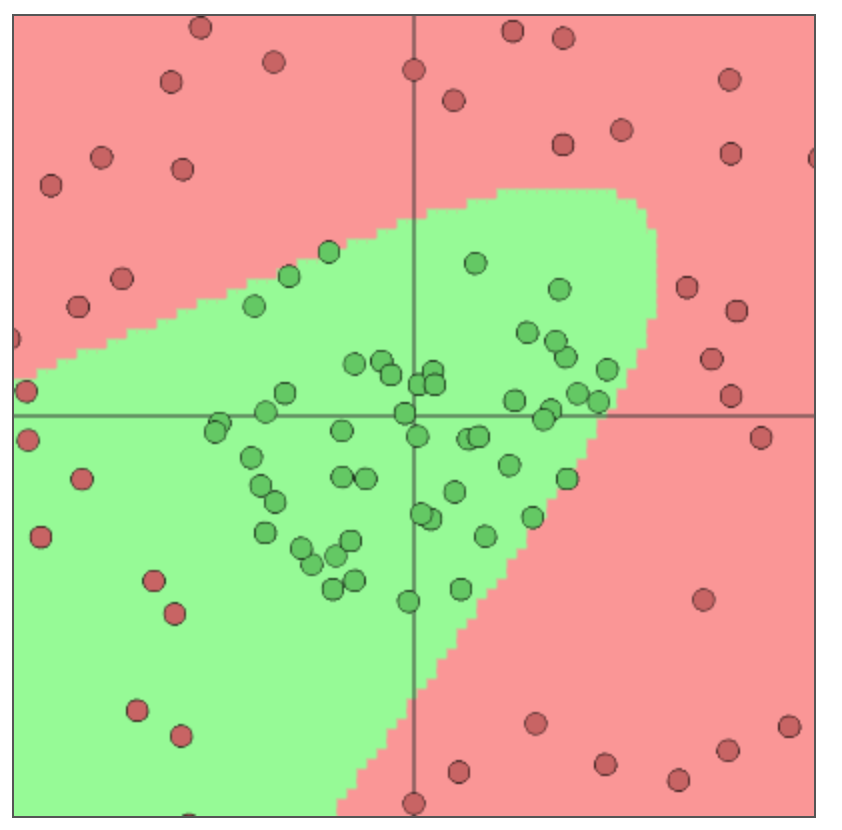
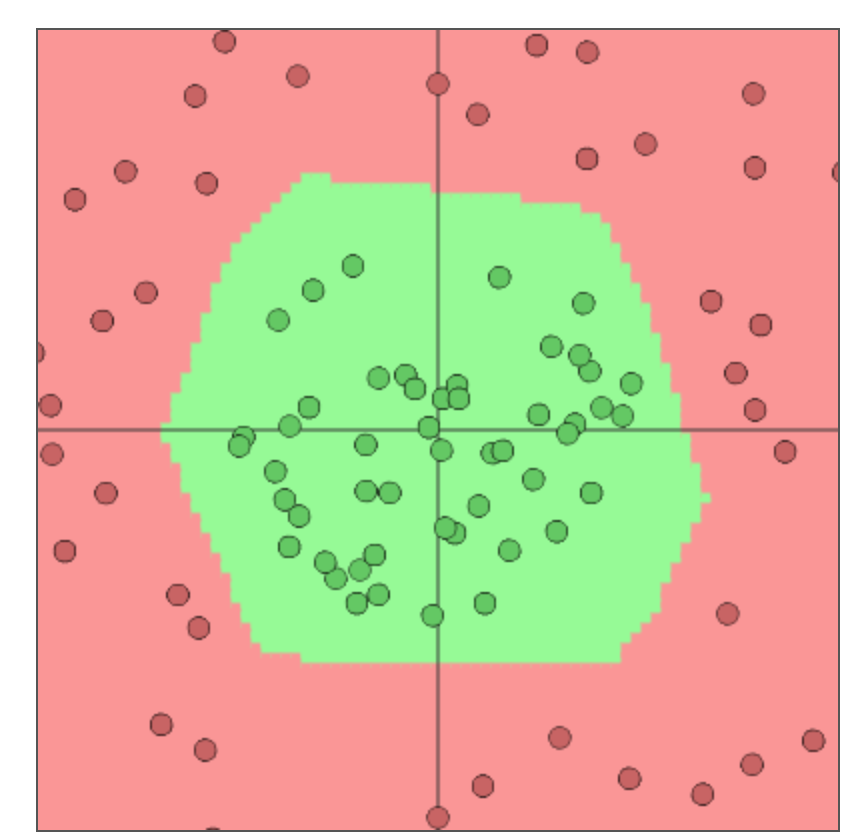
ニューラルネットは学習によって重みやバイアスの値が決められ、線形結合と非線形関数の繰り返しによってこの赤い領域と緑の領域を分ける境界線の関数を表現しています。ニューロンの数や活性化関数(後で説明します)の選び方で表現できる関数が変わってきます。順番に中間のニューロンの数が6で活性化関数がtanh、中間のニューロンの数が2で活性化関数がtanh、中間のニューロンの数が6で活性化関数がreluの学習結果になります。イメージとしてはニューロンの数が増えるほど直線の数がふえて、活性化関数にtanhを使うと直線同士のつなぎ目が丸く、reluを使うと尖るという感じだと思います。この理由はこの記事では触れないので教科書等で勉強してみてください。
順伝播計算
まずはじめに順伝播計算(Forward)について理解していきます。逆伝播計算に比べ順伝播計算は非常に簡単で理解しやすいと思います。順伝播計算は前の部分で行った$o=wx+b$のことを言います。まずは1入力1出力のニューラルネットワークを考えます。見やすくするため前の図の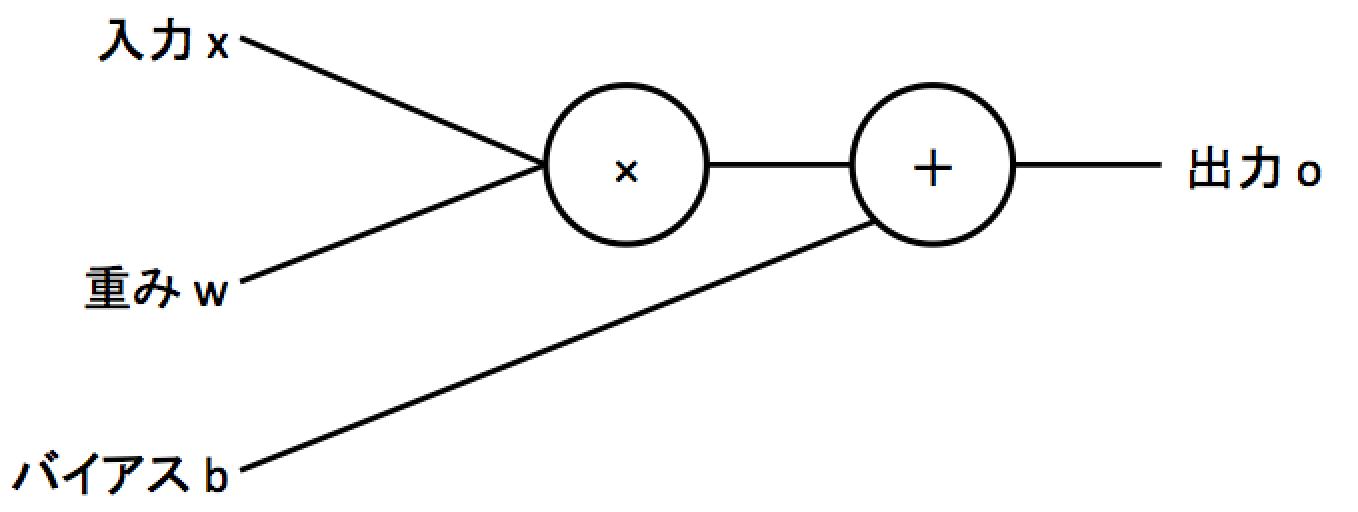
を
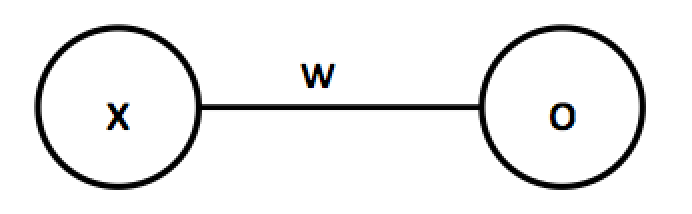
のように表現します。見やすさをと理解のしやすさのためバイアスは今後ないものとしていきます。1入力1出力は書くまでもないと思いますが以下のように単純な実装になります。
x = np.random.randn(1)
w = np.random.randn(1)
w*x
これを多入力1出力に拡張します。
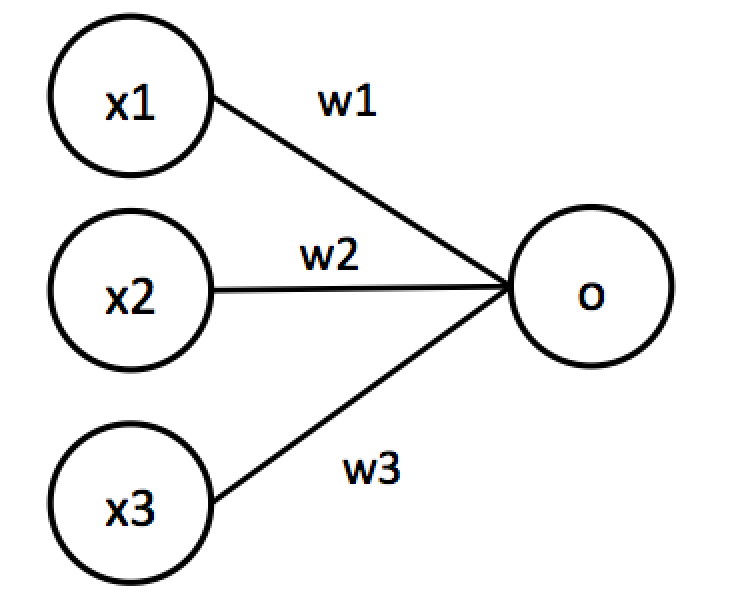
この計算は$o=w_1x_1+w_2x_2+w_3x_3$と表現できます。この式はベクトルの内積そのものなので以下のように実装できます。
x = np.random.randn(1,3)
w = np.random.randn(3,1)
np.dot(x,w)
次に1入力多出力を考えます。
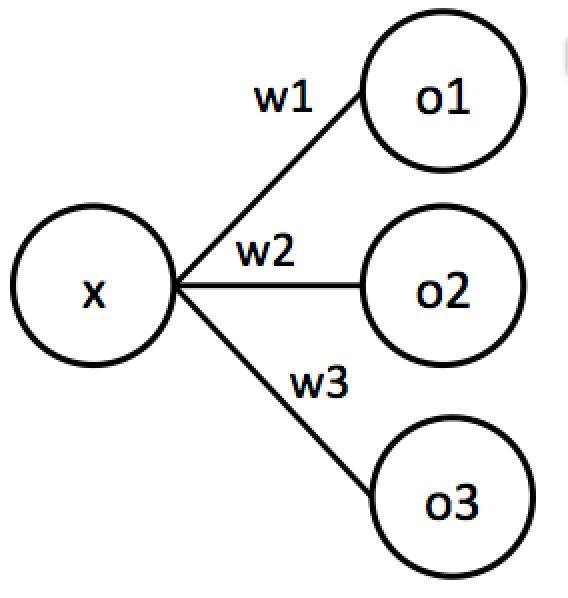
これは$o_1=w_1x, o_2=w_2x, o_3=w_3x$と表現できます。これはoとwを$\vec{o}={o_1, o_2, o_3}, \vec{w}={w_1, w_2, w_3}$のように定義すると$\vec{o}=x\vec{w}$と書き直せます。これは以下のように実装できます。
x = np.random.randn(1,1)
w = np.random.randn(1,3)
np.dot(x,w)
最後に多入力、多出力を考えます。
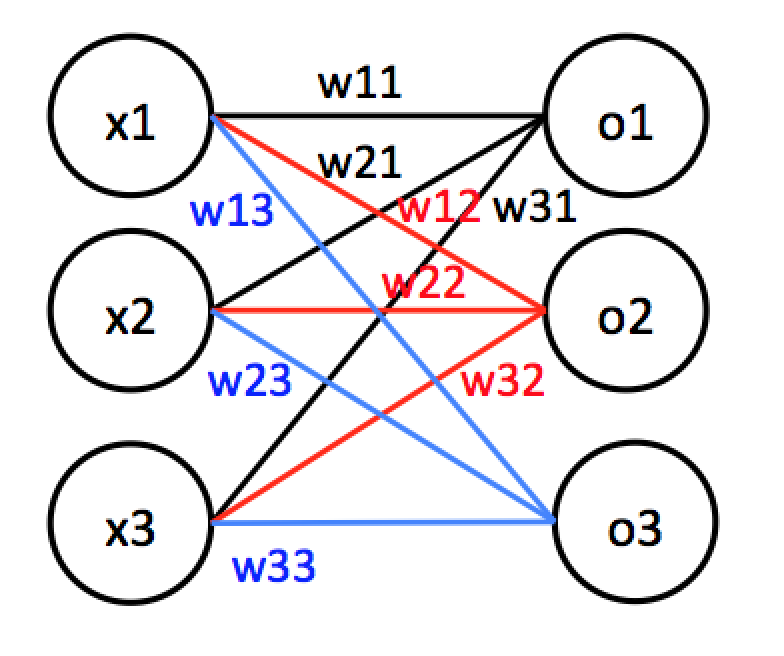
これは式にすると$o_1=w_{11}x_1+w_{21}x_2+w_{31}x_3$, $o_2=w_{12}x_1+w_{22}x_2+w_{32}x_3$, $o_3=w_{13}x_1+w_{23}x_2+w_{33}x_3$となります。ベクトルに直すと$\vec{x}={x_1,x_2,x_3}$, $\vec{w_1}={w_{11},w_{21},w_{31}}$, $\vec{w_2}={w_{12},w_{22},w_{32}}$, $\vec{w_3}={w_{13},w_{23},w_{33}}$となり、計算としては$o_1=\vec{w_1}\vec{x}$, $o_2=\vec{w_2}\vec{x}$, $o_3=\vec{w_3}\vec{x}$となります。これは行列積を使って表現可能で、各値を行列で以下のように表現します。
X=\begin{matrix} x_1 & x_2 & x_3 \end{matrix},
W=\begin{matrix} w_{11} & w_{12} & w_{13} \\
w_{21} & w_{22} & w_{23} \\
w_{31} & w_{32} & w_{33} \end{matrix},
O=\begin{matrix} o_1 & o_2 & o_3\end{matrix}
すると計算としては$O=XW$と表現可能です。かなりすっきりと表現ができました。行列に慣れていない人は実際に手を動かして確認して見てください。これを実装すると以下のようになります。
X=np.random.randn(1,3)
W=np.random.randn(3,3)
np.dot(X,W)
これで順伝播については終わりですが実際はバイアスを足し合わせます。最終的にこれを以下のように何層にも繋げていくと多層ニューラルネットワークになります。
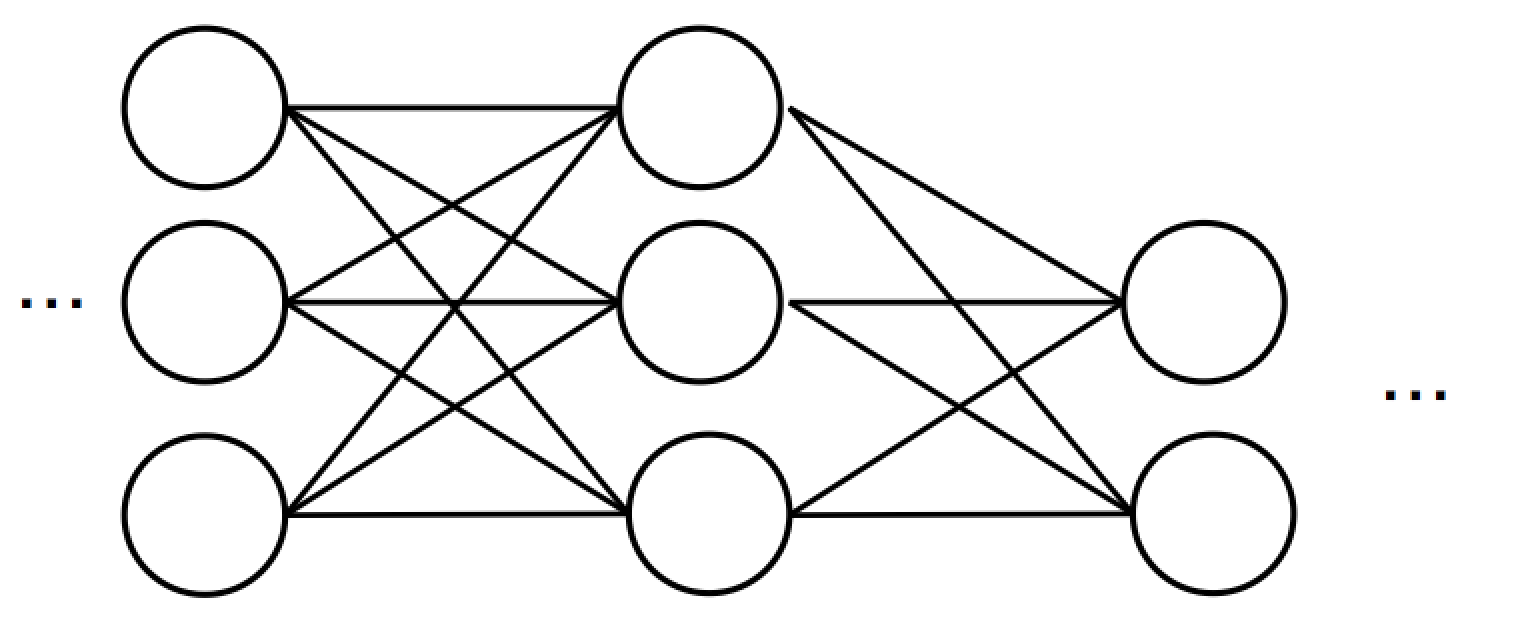
基本的には前の層で得られた出力Oを次の層のニューラルネットワークの出力Xとみなして同じ計算をしていくだけです。
X=np.random.randn(1,3)
layer1_W=np.random.randn(3,2)
layer2_W=np.random.randn(2,1)
layer1_O=np.dot(X,layer1_W)
layer2_O=np.dot(layer1_O, layer2_W)
重みとバイアスの更新
順伝播の次はどのようにして重みとバイアスの値を学習していくかについて理解します。まずニューラルネットを$f(X)=w_1x_1+w_2x_2+...+w_nx_n$のような一つの関数とします(ただし、$X={x_1,x_2,...,x_n}$)。これに対し重みを以下の式を用いて更新します。
w_i^{new}=w_i-lr\frac{\partial{f(x)}}{\partial{w_i}}
$lr$は学習率(Learning Rate)と呼ばれるものでどのくらい値を変更するかをコントロールするものになります。学習率は大きすぎても小さすぎても学習がうまくいきません。近年のニューラルネットの文脈では0.1~0.0001くらいまでの値をとることが多いですが、基本的にどれくらいの値が適切かはわからないので経験と感によるところが多いです。$\frac{\partial{f(x)}}{\partial{w_i}}$は$f(X)$を$w_i$について微分したもので上の$f(x)$定義でいくと$\frac{\partial{f(x)}}{\partial{w_i}}=x_i$となります。バイアスについても同様の計算で$w$を$b$に置き換えるだけです。なぜこれで出力値が目標の値になるように重みが更新されるかは今回は割愛します。一番重要な部分ではあるのですが重要な部分だけに高校数学のレベルで直感的な理解をすると問題が起こる可能性があるためまた機会があれば別な記事で解説します。
本題に戻って、上記の微分は一層のニューラルネットワークの場合は非常に簡単に計算が可能ですが一般的に用いられる多層ニューラルネットではそうもいきません。最初に書きましたが、ニューラルネットワークは順伝播のところで説明した線形結合の後に非線形関数を使った変換を行います。非線形関数を使うというのは以下のように計算することです。
o = w_1x_1+w_2x_2+w_3x_3,\:g(x)=\frac{1}{1+\exp(-x)},\:o'=g(o)=\frac{1}{1+\exp(-o)}=\frac{1}{1+\exp(-(w_1x_1+w_2x_2+w_3x_3))}
ちなみに上記の$g(x)$はsigmoid関数と呼ばれる非線形関数でニューラルネットでよく用いられていた関数です(最近は出力層以外であまり使われません)。このようにニューラルネットの出力にかます非線形関数を活性化関数と言います。この最終的な出力$o'$を特定の$w_1$について微分するのは少々難しいですが、この程度ならまだ頑張れば計算できます。しかしこれが以下の図のように多層になった場合を考えます。
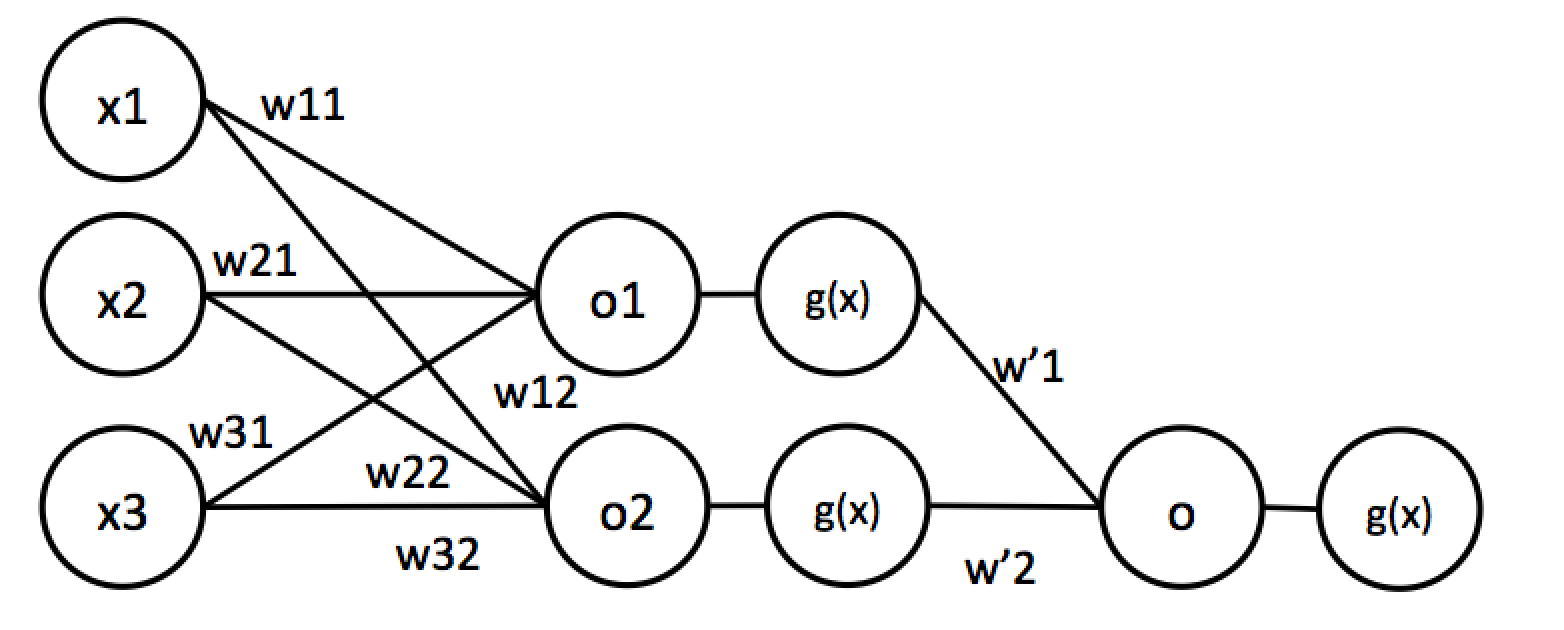
これを数式で書くと以下のようになります。
o_{1} = w_{11}x_1+w_{21}x_2+w_{31}x_3,\:o_{2} = w_{12}x_1+w_{22}x_2+w_{32}x_3,\\
o'_{1}=g(o_1),\:o'_{2}=g(o_2),\\
o=w'_1o'_1+w'_2o'_2,\:o'=g(o)
最終的な$o'$を頭から書くと以下のようになります。
o'=\frac{1}{1+\exp(-(w'_1\frac{1}{1+\exp(-(w_{11}x_1+w_{21}x_2+w_{31}x_3)}+w'_2\frac{1}{1+\exp(-(w_{12}x_1+w_{22}x_2+w_{32}x_3)})}
例えばこれを$w_{11}$について微分するのは非常に困難です。これがディープニューラルネットのように何十層にもわたると途方もない計算になります。これを効果的に計算するために次に紹介する逆伝播計算が用いられます。
逆伝播計算
逆伝播計算を行うために連鎖律(Chain Rule)という概念が重要になります。連鎖律は以下のような式が成り立つことを言います。
\frac{\partial{f(x)}}{\partial{w}}=\frac{\partial{f(x)}}{\partial{o}}\frac{\partial{o}}{\partial{w}}
すなわち、$f(X)$を$w$という変数について微分しようとした際、$f(x)$を$o$について微分したものと$o$を$w$について微分したものの掛け算で表せるというものです。イメージとして$\partial{o}$を約分すれば元と同じになるという感じです。例えば以下のようなものに適用してみます(連鎖律を使わなくても解けます)。
o=w+z,\:f(x)=(w+z)y=oy,\\
\frac{\partial{o}}{\partial{w}}=1,\:\frac{\partial{f(x)}}{\partial{o}}=y,\:\frac{\partial{f(x)}}{\partial{w}}=\frac{\partial{f(x)}}{\partial{o}}\frac{\partial{o}}{\partial{w}}=y
上記の計算は連鎖律を使わなくても計算できますが先ほどのsigmoid関数を用いた多層のものに適用する場合には非常に有効な計算方法です。
次に実際のニューラルネットに対して逆伝播計算を行っていきます。まずは簡単な1入力1出力のニューラルネットを考えます。
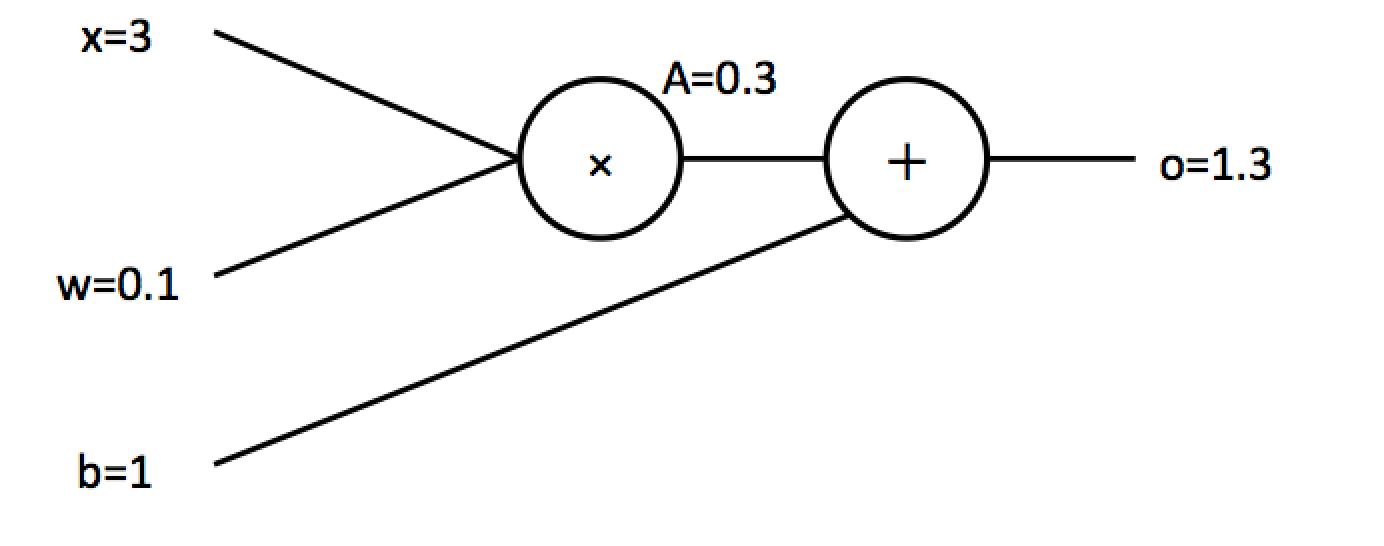
このニューラルネットは$f(x)=wx+b$と表現可能で中間的な出力として$A=wx$としましょう。目標として重みを更新するのに必要な$\frac{\partial{f(x)}}{\partial{w}}$とバイアスの更新に必要な$\frac{\partial{f(x)}}{\partial{b}}$を計算することを考えます。まず$\frac{\partial{f(x)}}{\partial{b}}$を計算します。$f(x)=A+b$と表現が可能なので$f(x)$の$b$についての微分は$\frac{\partial{f(x)}}{\partial{b}}=1$となります。次に$\frac{\partial{f(x)}}{\partial{w}}$を計算します。連鎖律を用いると$\frac{\partial{f(x)}}{\partial{w}}=\frac{\partial{f(x)}}{\partial{A}}\frac{\partial{A}}{\partial{w}}$と表現ができ、$\frac{\partial{f(x)}}{\partial{A}}=1$, $\frac{\partial{A}}{\partial{w}}=x=3$となるので$\frac{\partial{f(x)}}{\partial{w}}=3$となります。逆伝播の様子を図に示すと以下の青で示されたものになります。
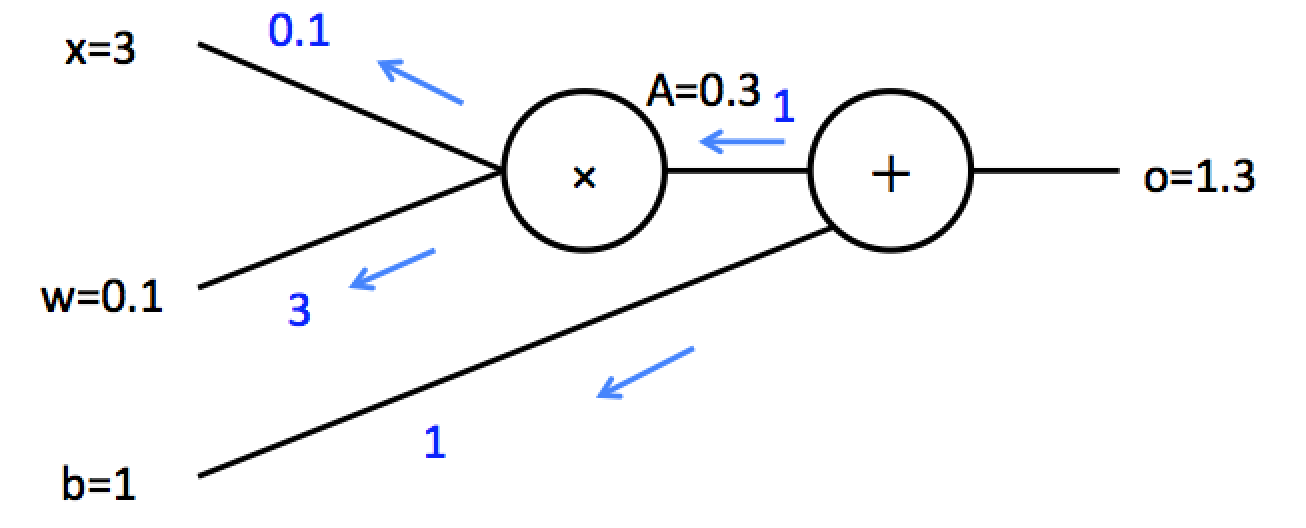
この逆伝播計算は非常に強力です。例えば前にあげたsigmoid関数の微分は以下のようになることが計算で求まります(実際に計算してみてください)。
f(x)=\frac{1}{1+\exp(-x)},\\
f'(x)=f(x)(1-f(x))=\frac{1}{1+\exp(-x)}(1-\frac{1}{1+\exp(-x)})
次に、sigmoid関数自体の微分を計算することなく$\frac{\partial{
f(x)}}{\partial{x}}$の値を逆伝播計算で求めてみます。sigmoid関数を以下のように表現します。
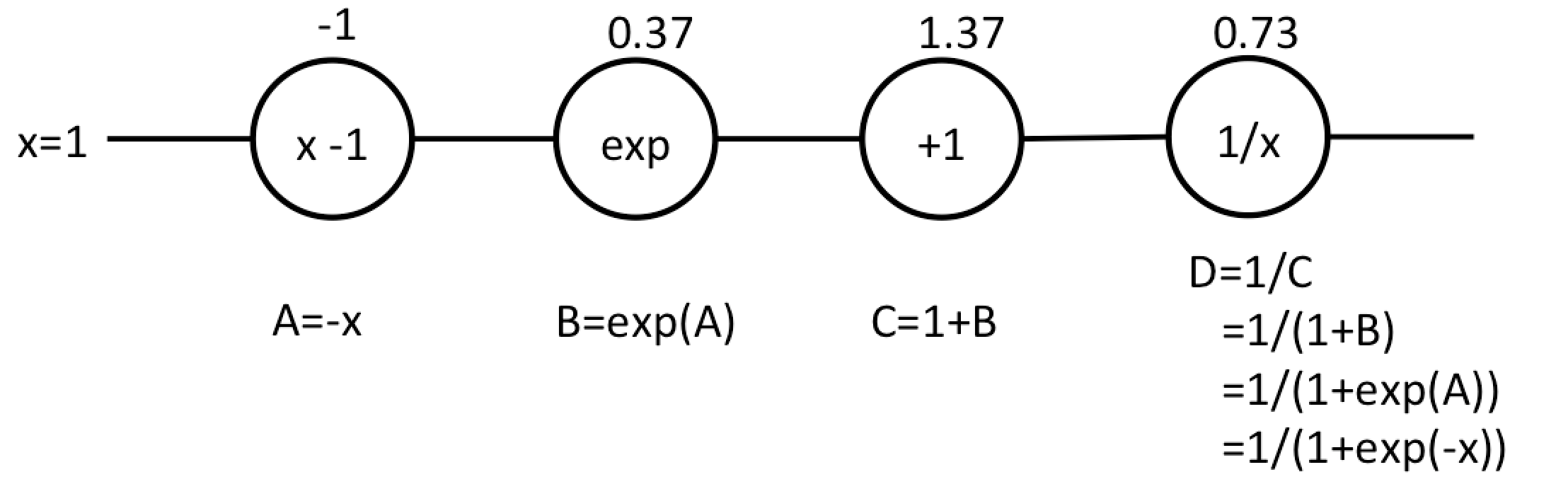
ここでは$D$がsigmoid関数を表しています($D=f(x)$)。これを逆伝播計算していきます。
\frac{\partial{D}}{\partial{C}}=(\frac{1}{C})'=\frac{-1}{C^2}=\frac{-1}{(1.37)^2}=-0.53\\
\frac{\partial{D}}{\partial{B}}=\frac{\partial{D}}{\partial{C}}\frac{\partial{C}}{\partial{B}}=(-0.53)(1+B)'=(-0.53)(1)=-0.53\\
\frac{\partial{D}}{\partial{A}}=\frac{\partial{D}}{\partial{B}}\frac{\partial{B}}{\partial{A}}=(-0.53)(\exp(A))'=(-0.53)(\exp(A))=(-0.53)(0.37)=0.2\\
\frac{\partial{D}}{\partial{x}}=\frac{\partial{D}}{\partial{A}}\frac{\partial{A}}{\partial{x}}=(-0.2)(-x)'=(-0.2)(-1)=0.2
実際にsigmoid関数の微分である$f'(x)=f(x)(1-f(x))$に$x=1$を代入してみると同様の結果が得られるはずです(有効数字2桁で計算しているので気をつけて下さい)。
話をニューラルネットワークに戻します。次に以下のような多層のニューラルネットの逆伝播を考えます。
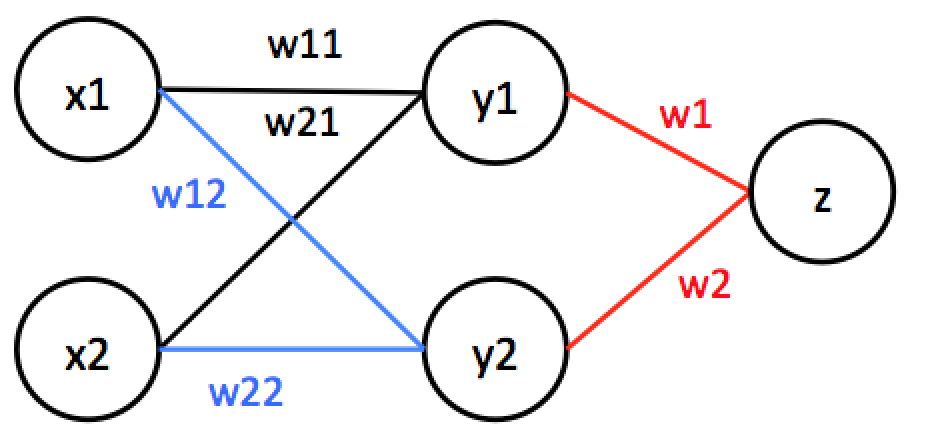
見にくくなりますが、以下のように表現を直します。
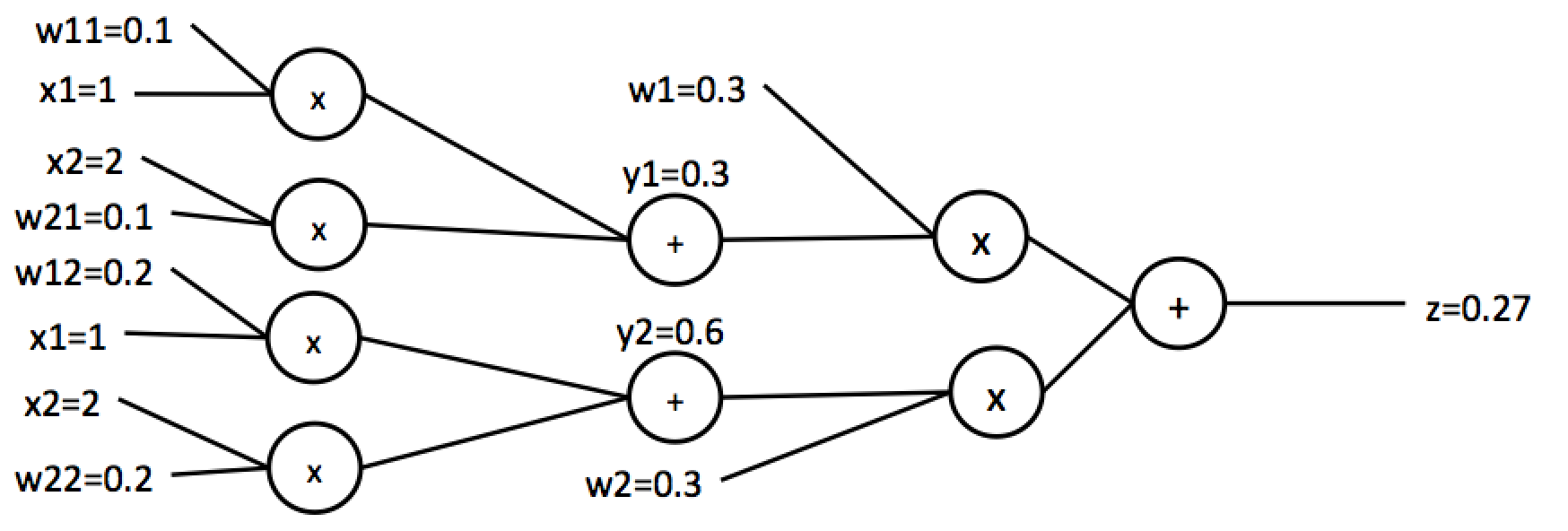
このニューラルネットの逆伝播計算を行います。途中過程は省略して結果だけ示すと以下のようになります。実際に計算してみてください。
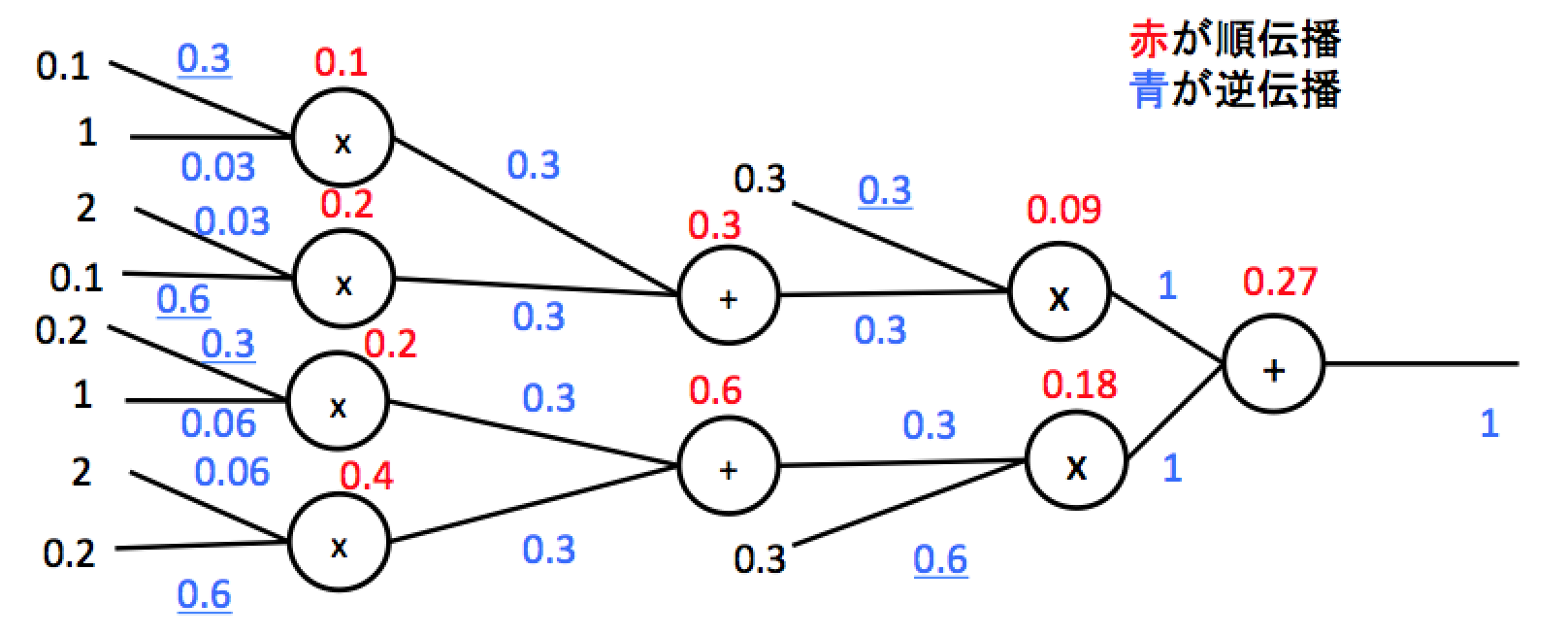
下線が付いている値が実際にパラメータの更新に用いる$\frac{\partial{f(x)}}{\partial{w_i}}$になります。このようにして計算された値に学習率を掛け合わせて元の値から引くことで学習を行うことができます。
最後に順伝播、逆伝播、パラメータの更新の一連の流れを実装してみます。今回はバイアスのないものを実装していますが、理解できているかの確認として是非バイアスを加えたものを自分で実装してみてください。以下のようなnnクラスを定義します。
class nn():
def __init__(self, n_i, n_o, lr):
self.weight = np.random.randn(n_o, n_i)
self.input = None
self.grad = np.zeros((n_i, n_o))
self.lr = lr
def forward(self, x):
self.inputs = x.reshape(-1, 1) # 入力の値を保持
return np.dot(self.weight, self.inputs)
def backward(self, dx):
self.grad = np.dot(self.inputs.reshape(-1,1), dz.reshape(1,-1)).reshape(self.weight.shape) # wに関する微分計算
return np.dot(dz.reshape(1, -1), self.weight) # xに関する微分計算
def update(self):
self.weight -= self.grad*self.lr
forwardに関しては順伝播で実装したのと同様の実装です。入力の値を保持しているのは、逆伝播計算の際にwの微分値を計算するのに必要になるためです。実際に前の例を手計算すればわかると思いますが、wに関する微分値は前から伝播してきた微分値かける入力xの値になっています。backwardでは微分の計算に行列積を用いています。順伝播のところでやったように一つ一つの計算を書き下してみると全てのwに対する微分が行列積で一気に計算できることがわかると思います。同様にxに関する微分値も前から伝播してきた微分値と重みの行列積で計算が可能です。実際に内積で計算できるか確認すると理解できてるかわかるので確認してみてください。wの微分値(grad)が計算できれば学習率をかけ合わせて元の値から引けば重みの更新ができます。
from nn import nn
fc = nn(10, 2, 0.1)
x = np.random.randn(10, 1)
fc.forward(x)
grad = np.random.randn(1,2) # 前から来る微分値
fc.backward(grad)
fc.update()
以上のように重みを更新することができます。上記では前から来る微分値を乱数で生成していますが、実際には目標値との誤差を計算する誤差関数というものを使って計算します。
実際にニューラルネットワークのモデルを組む際には層と層の間に活性化関数(非線形関数)を挟みます。今回はsigmoid関数を実装してみます。前に書いたようにforwardもbackwardも式が出ており、backwardに関しては順伝播計算の計算結果を使って求められるため以下のように実装が可能です。
class sigmoid():
def __init__(self):
self.output = None
def forward(self, x):
self.output = 1/(1+np.exp(-x))
return self.output
def backward(self, dx):
return self.output * (1 - self.output)
前に書いた式をそのまま記述するだけで実装が可能です。sigmoid関数には学習するパラメータがないためupdate関数や微分値を保持する必要ありません。実際にこのsigmoid関数を使って多層ニューラルネットのモデルを作ると以下のようになります。
from nn import nn
from sigmoid import sigmoid
fc1 = nn(10, 5, 0.1)
sig1 = sigmoid()
fc2 = nn(5, 2, 0.1)
sig2 = sigmoid()
x = np.random.randn(10, 1)
sig2.forward(fc2.forward(sig1.forward(fc1.forward(x))))
grad = np.random.randn(1,2)
fc1.backward(sig1.backward(fc2.backward(sig2.backward(grad))))
fc1.update()
fc2.update()
誤差関数
最後に誤差関数について説明します。順伝播、逆伝播とネットワークの学習に必要なものは揃ったのであとはどのようにしてニューラルネットの出力が目標値に近づくように重みを更新するかだけです。今まではニューラルネットワークの入力から出力までを一つの$f(x)$という関数で表現してこれを$w$について微分していました。しかしこの値で重みを更新してもデタラメな値に更新されていくだけで使い物になりません。そのためニューラルネットワークの最後に誤差関数と呼ばれる目標値との差を表す関数をかませて、入力から誤差関数までを一つの$f(x)$という関数として考えます。この誤差関数を含めた$f(x)$を微分した値で更新することで出力値が目標値に近づくように重みを更新することができるようになります。
機械学習では問題に合わせた誤差関数を用いてモデルの学習を行います。今回は実装や理解の簡単さから平均二乗誤差(mean squared error)を用います。平均二乗誤差は回帰に使われる誤差関数の一つで以下のように定義されます。
f(x)=\frac{1}{n}\sum_{i=1}^n(y_i-x_i)^2\\
\frac{\partial{f(x)}}{\partial{x_i}} = \frac{2}{n}(y_i-x_i)
ここで$x_i$はネットワークのi番目の出力、$y_i$はi番目の出力に対応した目標の値になります。ニューラルネットワークは設定された誤差関数の値を最小にすることを目標とします。なので平均二乗誤差を用いると$x_i$と$y_i$の値の差がゼロ、すなわち全く同じ値になるように重みが更新されていきます。以下、実装例になります。
class MSE():
def forward(self, x, y):
return np.square(y.reshape(-1)-x.reshape(-1)).mean()
def backward(self, x, y):
return 2*(y.reshape(-1) - x.reshape(-1)).mean()
あとはデータさえ用意ができれば回帰問題を解くことが可能です。以下に実装例を示します。
from nn import nn
from sigmoid import sigmoid
from MSE import MSE
fc1 = nn(10, 5, 0.1)
sig1 = sigmoid()
fc2 = nn(5, 2, 0.1)
sig2 = sigmoid()
mse = MSE()
x = np.random.randn(10) # 学習データ生成
t = np.random.randn(2) # 教師データ生成
for i in range(100):
out = sig2.forward(fc2.forward(sig1.forward(fc1.forward(x))))
loss = mse.forward(out, t)
print(loss)
grad = mse.backward(out, t)
fc1.backward(sig1.backward(fc2.backward(sig2.backward(grad))))
fc1.update()
fc2.update()
上記コードを実行すると出力されるlossの値が小さくなっていくのがわかるはずです。今回はデータを乱数で生成していますが実際のデータを読み込めばそのデータに適した学習をしてくれます。
誤差関数は様々なものがあるので是非調べて実装してみてください。そうすると各々の誤差関数の特性が理解でき、自分の解きたい問題に合わせた独自の誤差関数なども設計できるようになると思います。
まとめ
ニューラルネットワークの学習についての理解・実装を高校数学のレベルで解説してみました。ニューラルネットのバイアスがある場合の実装や実際データを用意して学習するところは理解できているかの確認を兼ねて自身で試してみてください(学習の部分を実装するのは面倒だっただけですごめんなさい)。
なぜ微分値で更新すると最適化ができるのか、勾配消失、勾配爆発、パラメータの初期化、ハイパーパラメータの重要性、sigmoid関数以外の活性化関数、CNN、RNNなどまだまだニューラルネットワークについては説明することがたくさんありますが今回はこんなところで終わりたいと思います。
勢いで書いた記事なので誤字脱字、実装ミス、その他もろもろあると思うので気をつけてください。あとは実際に書籍などでちゃんとした理論を勉強することをお勧めします。