19/3/24 初版
19/3/24-25 語句,レイアウトを数回修正し,Qiitaの関連記事を1つ追加.
1. はじめに
本記事では FreeFEM で P2 要素用メッシュを出力する一つの方法を紹介する.誤りなどあるかもしれないが,不都合が生じても責任は負えない.また,ソフトウェアのバージョンアップと共に仕様が変更されることもあり得る.
FreeFEM は FEMにより偏微分方程式の数値計算を行うためのソフトウェアである (公式 web ).これまで 「FreeFem++」という名称が使われていたが,変更があったらしい.
QiitaにおけるFreeFEM の解説は t_kemmochi 氏の FreeFem++の紹介が詳しいので,このソフトの紹介は本記事ではしない.本,Web上の情報も多くあるが,ここで引用されている文献を参照されたい.なお,本記事ではここの[データの構造]
(https://qiita.com/t_kemmochi/items/418bdc55e4937381711e#%E3%83%87%E3%83%BC%E3%82%BF%E3%81%AE%E6%A7%8B%E9%80%A0)の知識を仮定する.他,Qiita の FreeFEM の記事として wakabame 氏による FreeFem++ と Python を使って数学 gif を作ってみよう があり,可視化について書かれている.
本記事では FreeFEM で得られた有限要素解を出力し,別のソフトで描画させたり,別のプログラムで解の精度を検証したりする使用法を想定する.区分的2次多項式を使ったP2要素による計算はP1要素と比較し高精度であるが,出力されるデータは節点値のみである.これを他で利用するにはP2要素用のメッシュデータが必須である.しかし,その説明はあまり見かけないように思える.筆者が見たのは公式Documentの情報のみである.
筆者は,いつもは,FreeFEMで出力されるmshファイルを加工してP2要素用のメッシュデータを作成しているが,節点番号の付け方がFreeFEMのそれと一致しないので,そのデータを利用するという目的には不向きであった.FreeFEMの機能だけで作れればより簡単である.本記事ではそれを出力する一つの方法を示す.
実行環境と文献
筆者 は Windows 上で FreeFem++ ver. 3.42 を使っている.ただし,今回参照する Documentation は ここで公開されている pdf 版 Release 4.0 (Mar 22, 2019) のそれである(このリンクが安定しているか分からないので注意).この記事の情報は pdf ドキュメントの情報に倣っている(おまけの節を除く)のでそれを引用するように努めた.
2. プログラムと出力
以下の p2test.edp の実行により,作業ディレクトリに「Th.msh」「elnp2.dat」「npxy2.dat」が作成される.
mesh Th = square(3, 3);
savemesh(Th,"Th.msh");
fespace Vh(Th, P2);
int kdf;
kdf = Vh.ndofK; // == 6
{
ofstream ff("elnp2.dat");
// Th.nt : The number of triengles
ff << Th.nt << " " << kdf << endl;
for (int k = 0; k < Th.nt; k++){
for (int i = 0; i < kdf; i++){
ff << Vh(k,i) + 1 << " ";
}
ff << endl;
}
}
Vh showx, showy;
showx = x; showy = y;
{
ofstream ff("npxy2.dat");
ff << Vh.ndof << " " << 2 << endl;
ff.precision(10);
for (int i = 0; i < Vh.ndof; i++){
ff << showx[][i] << " " << showy[][i] << endl;
}
}
実行により,作業ディレクトリに「Th.msh」「elnp2.dat」「npxy2.dat」が作成される.
16 18 12
0 0 4
0.333333333333 0 1
0.666666666667 0 1
1 0 2
(中略)
0 1 4
0.333333333333 1 3
0.666666666667 1 3
1 1 3
1 2 6 0
1 6 5 0
2 3 7 0
2 7 6 0
(中略)
10 11 15 0
10 15 14 0
11 12 16 0
11 16 15 0
(以下略)
18 6
24 37 28 29 25 33
24 28 18 20 21 25
37 46 38 40 39 42
37 38 28 32 29 39
(中略)
19 27 14 11 12 15
19 14 10 5 7 12
27 36 22 34 23 31
27 22 14 13 11 23
49 2
0 1
0 0.8333333333
0.1666666667 1
0 0.6666666667
(中略)
0.6666666667 0
1 0
0.8333333333 0
1 0.1666666667
3. メッシュデータの観察
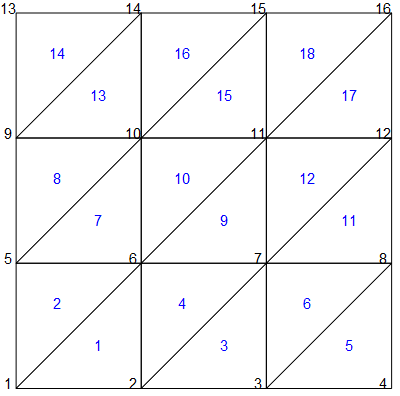
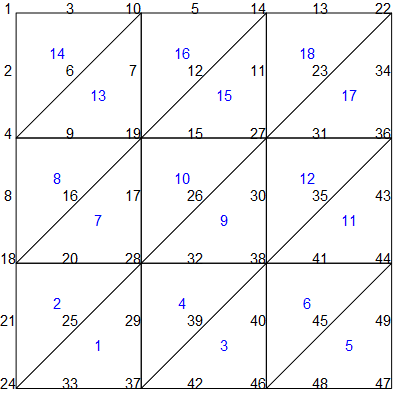
Th.mshのデータと,elnp2.datとnpxy2.datのP2要素データに対応するメッシュの節点番号と要素番号をそれぞれ図に示した(この可視化はFreeFEMの機能外).青字で要素番号を,黒字で大域的な節点番号を示している.
Th.mshはP1メッシュの情報である.以下にここからの情報を抜粋するが,それぞれ節点・座標対応表と,要素・節点対応表である.
0 0
0.333333333333 0
0.666666666667 0
1 0
(中略)
0 1
0.333333333333 1
0.666666666667 1
1 1
1 2 6
1 6 5
2 3 7
2 7 6
(中略)
10 11 15
10 15 14
11 12 16
11 16 15
次にP2メッシュの番号付けを見てみる.npxy2.datは節点・座標対応表,elnp2.datは要素・節点対応表である.elnp2.datの1行目
24 37 28 29 25 33
は図の番号1の要素の大域的な節点番号に対応している.一つの要素における局所的な節点番号は三角形の3頂点を反時計まわりに0 1 2 とつけ,0の対辺上の中点を3, 1の対辺上の中点を4, 2の対辺上の中点を5としていることが観察できる.FreeFEMの仕様では,大域的な節点番号はmshファイルのP1用データの拡張ではないことが分かる.
4. プログラムの説明
以下,ページ数を書くことがあるが,公式 Document の対応するページである.
プログラムではP1用Friedrichs-Keller 型のメッシュを
mesh Th = square(3, 3);
で作成し,このメッシュの情報を
savemesh(Th,"Th.msh");
でファイルに書き出している(p. 27).
fespace Vh(Th, P2);
でP2有限要素空間 Vh を定義し,p. 188 に従い,
ff << Vh(k,i) + 1 << " ";
で要素・節点対応表を出力している.ここで番号付けが1から始まるように+1をしている.mshファイルでは番号付けが1から始まるので,それにそろえるためである.Wh.ndof, Wh.ndofK はそれぞれ総節点数,1つの要素の節点数(ここでは6)を示している.
次に p. 97の方法に倣い,
Vh showx, showy; showx = x; showy = y;
ff << showx[][i] << " " << showy[][i] << endl;
としてP2要素用の節点・座標対応表を出力している.ここで,
ff.precision(10)
で小数点以下何桁書き出すかを指示している(p. 346).
5. おわりに
本記事ではFreeFEMからP2要素のデータを出力する方法を示した.扱ったのは節点・座標対応表と,要素・節点対応表のみである.u に有限要素解が入っているとき,出力ストリーム ff を同様に定義し,
ff << u[];
とすると,各節点における有限要素解の値が出力される(p. 27).有限要素関数の出力は節点・座標対応表の出力の時に既に行っている.FreeFEMから有限要素関数を取り出して,別のプログラムで利用することができる.基底関数を使い補間を行い,可視化をすることもできるだろう.ここではP2要素を扱ったが,他の要素についても同様にできることが予想される(試していないが).
用途によっては他のデータも必要だと思われる. mshファイルには境界辺と節点の対応表があるが,P2要素のそのような情報の取り出し方は不明である(なお,おまけも参照のこと).
A. おまけ
上で定義されたP2有限要素空間 Vhを使い,
Vh showlabel;
showlabel = label;
とし,showlabelを出力すると,各節点について境界に乗っていればその境界ラベルを,乗っていなければ0が表示される.これはp. 98のregionの方法がlabelにも適応できるだろうと類推したものであるが,しかし,この使用法は Document に見つけられなかったので,正式なサポートはないと考えられる.