はじめに
先日、「サザエさんじゃんけん研究所」1様の「サザエさんじゃんけん白書」が話題になりました。
過去のサザエさんの手を分析し、傾向と対策を見出すという企画?です。
じゃんけんで何を出せば勝てるか人間が推測できるなら、コンピュータ(プログラム)でもできるに違いない、ということで勝手にシリーズ化してしまったネタです。
これまでのあらすじ
問題設定
くどいからもういいか。。。
あらすじのどちらかの記事をご覧ください。
今回は回帰分析
今までの2回はサザエさんの手を直接予想するプログラムだったのですが、今回は「ある手を自分が出したときの利益」を考えてみます。言ってみれば、サッカーの試合などでいう「勝ち点」のようなものですね。
もちろん同じ状況と戦略だからといって、同じ結果になるとは限りませんが、監督は「勝ち点が最も多く取れそうな戦略」で試合に臨んでいるはずです。
今回の戦略では、過去の相手の手の傾向を見たときに
- グーを出せば勝ち点Xが取れる
- チョキを出せば勝ち点Yが取れる
- パーを出せば勝ち点Zが取れる
という値を予想して、その数値が最も高くなるような手を出すようにします。
この勝ち点を予想するために、状況とその時の相手の手の組み合わせを「回帰分析」2という考え方でモデル化します。
なお、勝ち点の決め方には自由度があって
- 勝ちの場合、勝ち点は1
- 負けの場合、勝ち点は0
まではいいとして、
- あいこ(引き分け)の場合、勝ち点は?
については調整の余地があります。
これは実際に色々試してみて勝率が高くなりそうな値を決めるしかありません。
選んだ特徴量
1つ前のSVM編と同様に、
- 放送週が各月の1週目かどうか(1次元: 1週目なら1、それ以外なら0)
- グー・チョキ・パーのそれぞれが現れていない週数(3次元)
- 前の回で現れていれば1、2回前で現れていれば2…
- 初回は便宜上 (1, 1, 1) から始めます。
の4次元データとします。
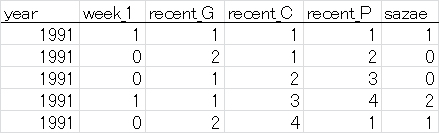
入力データは、以下の形式のテキストフォーマット(タブ区切り)で与えます。
データのフィルタリングのため、先頭に放送年の列を追加しています。
(先頭行はデータに含めません)
- 最終列はサザエさんの手で、0: グー、1: チョキ、2: パーを表す。
- 1行目は1991年11月第1週(便宜上、開始月は月の途中ですが1週目から始めます)で、サザエさんはチョキを出した。
- 2行目は1991年11月第2週で、前回はチョキ。今回はグー。
- 3行目は1991年11月第3週で、前回はグー、2回前はチョキ。今回はグー。
実際には、同様のフォーマットで1300行以上のデータが続きます。
モデルの更新については
- 1995年までのデータを使ってパラメータを学習し、1996年の1年間のデータを予測する。
- 1996年までのデータを使ってパラメータを学習し、1997年の1年間のデータを予測する。
- (以下略)
という感じで、今までのシリーズと同じにします。
アルゴリズム
前回使ったSVM(サポートベクターマシン)を回帰分析に応用した手法(SVR: サポートベクター回帰)があります。
サポートベクター回帰(Support Vector Regression, SVR)~サンプル数10000以下ならこれを使うべし!~ - データ化学工学研究室(金子研究室)@明治大学 理工学部 応用化学科
SVM編では、線形カーネルで結構うまく識別できることが分かりましたので、今回も線形カーネルで試してみましょう。
プログラム
Python 2.7とscikit-learn3を事前にインストールしてください。
scikit-learnは、pipを使うと以下のコマンドでインストールできます(numpyなどの関連パッケージも自動的にインストールされます)。
pip install scikit-learn
なお、プログラム作成には以下のドキュメントが非常に参考になりました。
学習・評価部分
# !/usr/bin/env python2.7
# -*- coding: utf-8 -*-
import numpy as np
import mydata
from sklearn.svm import LinearSVR
from sklearn.model_selection import GridSearchCV
from sklearn.multioutput import MultiOutputRegressor
I3 = np.identity(3, dtype=np.float32)
# 使用する特徴量
idx_features = np.r_[1:5]
# あいこの場合に与える利得。
# 勝ちの場合の利得を1とする。
# 大きいほどあいこを狙いやすくなる。
gain_draw = 0.55
## read data
data_orig = mydata.read()
win_total = 0
draw_total = 0
lose_total = 0
for year in xrange(1996, 2019):
# 前年までのデータで学習
data_train = data_orig[data_orig[:, 0] < year]
X_train = data_train[:, idx_features]
# 自分の出すべき手を直接学習
# 勝ちとなる手に1、あいことなる手にも小さい利得を与える
sazae_choice = data_train[:, -1]
y_train = I3[(sazae_choice + 2) % 3] # one-hot encoding
y_train += I3[sazae_choice] * gain_draw
# https://stackoverflow.com/questions/43532811/gridsearch-over-multioutputregressor
# 交差検定により最適なハイパーパラメータを決定してから学習
parameters = [{'estimator__epsilon': np.logspace(-3, 0, 10)}]
reg_cv = GridSearchCV(MultiOutputRegressor(LinearSVR(
dual=False, random_state=0, loss="squared_epsilon_insensitive"
)), parameters, n_jobs=-1)
reg_cv.fit(X_train, y_train)
reg = MultiOutputRegressor(LinearSVR(
dual=False,
epsilon=reg_cv.best_estimator_.estimator.epsilon,
loss="squared_epsilon_insensitive", random_state=0))
reg.fit(X_train, y_train)
# その年のデータでテスト
data_test = data_orig[data_orig[:, 0] == year]
X_test = data_test[:, idx_features]
sazae_choice_test = data_test[:, -1]
# 予測される利得の最も大きい手を選ぶ
# 0: G, 1: C, 2: P
mychoice = np.argmax(reg.predict(X_test), axis=1)
# 判定
judge = ((mychoice + 3 - sazae_choice_test) % 3)[sazae_choice_test >= 0]
win = (judge == 2).sum()
draw = (judge == 0).sum()
lose = (judge == 1).sum()
win_total += win
draw_total += draw
lose_total += lose
print "{0} Win: {1:3d}, Draw: {2:3d}, Lose: {3:3d} / Avg: {4:.2f}%".format(year, win, draw, lose, float(win)/(win+lose)*100)
# 相手の手を-1ラベルにした行について、自分の出すべき手を予測する
if (sazae_choice_test == -1).sum() > 0:
print reg.predict(X_test)[sazae_choice_test == -1]
print mychoice[sazae_choice_test == -1]
print "======"
print "<TOTAL> Win: {0:3d}, Draw: {1:3d}, Lose: {2:3d} / Avg: {3:.2f}%".format(win_total, draw_total, lose_total, float(win_total)/(win_total+lose_total)*100)
データ読み込み
# -*- coding: utf-8 -*-
import numpy as np
def read():
# read data
with open("input.txt", "r") as fr:
data = [[int(val) for val in l.split(None)] for l in fr]
return np.array(data, dtype=int)
データ
先程説明したフォーマットです。
元データは本家様のサイトからせっせとスクレイピングさせていただきました。m(_ _)m
1991 1 1 1 1 1
1991 0 2 1 2 0
1991 0 1 2 3 0
1991 1 1 3 4 2
1991 0 2 4 1 1
:
:
2018 0 3 1 4 2
2018 0 4 2 1 0
2018 0 1 3 2 -1
時系列にデータが並んでいて、下から2行目が前回放送(2018/8/19)の結果です。
今回は、これまでの結果に加えて、最後の行を追加しました。この行は、今度の放送(2018/8/26)に対する予想をするためのものです。
サザエさんの手を「-1」という特殊な値にすると、先ほど述べた「自分がグー、チョキ、パーを出したときの勝ち点の予想」を出すようにプログラムを書いています。
結果
以下のように実行します。結果が出るまで1分程度お待ちください。
python train_eval.py
実行結果はこちら。2018年は8月19日放送分までです。
1996 Win: 23, Draw: 18, Lose: 9 / Avg: 71.88%
1997 Win: 31, Draw: 11, Lose: 9 / Avg: 77.50%
1998 Win: 32, Draw: 10, Lose: 10 / Avg: 76.19%
1999 Win: 25, Draw: 11, Lose: 14 / Avg: 64.10%
2000 Win: 18, Draw: 22, Lose: 11 / Avg: 62.07%
2001 Win: 28, Draw: 15, Lose: 8 / Avg: 77.78%
2002 Win: 23, Draw: 21, Lose: 6 / Avg: 79.31%
2003 Win: 23, Draw: 16, Lose: 11 / Avg: 67.65%
2004 Win: 26, Draw: 12, Lose: 11 / Avg: 70.27%
2005 Win: 24, Draw: 12, Lose: 13 / Avg: 64.86%
2006 Win: 29, Draw: 13, Lose: 8 / Avg: 78.38%
2007 Win: 24, Draw: 14, Lose: 13 / Avg: 64.86%
2008 Win: 31, Draw: 12, Lose: 8 / Avg: 79.49%
2009 Win: 25, Draw: 19, Lose: 6 / Avg: 80.65%
2010 Win: 26, Draw: 16, Lose: 6 / Avg: 81.25%
2011 Win: 30, Draw: 16, Lose: 5 / Avg: 85.71%
2012 Win: 28, Draw: 11, Lose: 10 / Avg: 73.68%
2013 Win: 28, Draw: 14, Lose: 9 / Avg: 75.68%
2014 Win: 31, Draw: 16, Lose: 4 / Avg: 88.57%
2015 Win: 32, Draw: 11, Lose: 7 / Avg: 82.05%
2016 Win: 27, Draw: 11, Lose: 12 / Avg: 69.23%
2017 Win: 34, Draw: 6, Lose: 8 / Avg: 80.95%
2018 Win: 18, Draw: 9, Lose: 6 / Avg: 75.00%
[[0.53150611 0.56800457 0.41944163]]
[1]
======
<TOTAL> Win: 616, Draw: 316, Lose: 204 / Avg: 75.12%
なんと勝率が**75.12%**という結果に。
あいこの勝ち点は、いろいろ試してみた結果0.55を採用しています。
以下の部分の数値を変えることで、勝ち点を変えたときの予想ができます。
gain_draw = 0.55
出力の以下の部分が予想結果です。
[[0.53150611 0.56800457 0.41944163]]
[1]
- 1行目は、グー、チョキ、パーを出したときに取れそうな勝ち点の予想
- 2行目は、勝ち点が最も多く取れそうな手(0: グー、1: チョキ、2: パー)
を表します。
グーのとき0.53点、チョキのとき0.57点、パーのとき0.42点。僅差ではありますが、2018/8/26の放送(投稿時点では放送前)では「チョキ」を出すのが良さそうですね。さてどうなる?
(2018/8/26 20:35) サザエさんは「グー」を出しましたので、負けですね。。。
考察
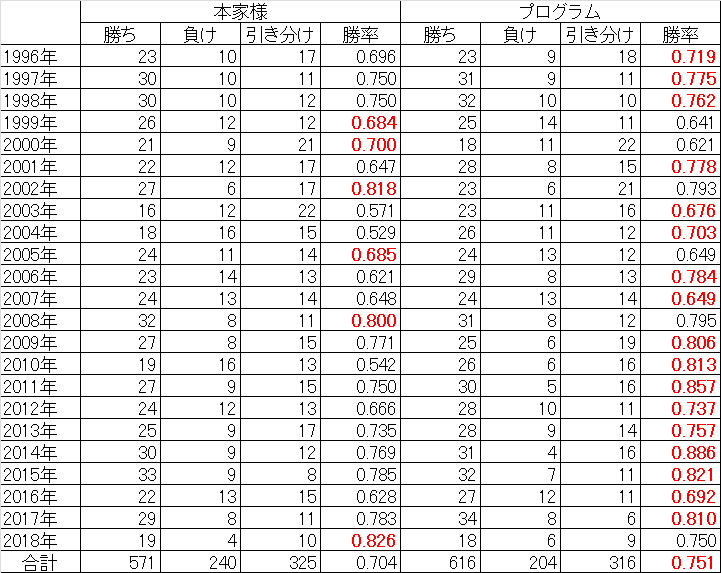
年ごとの予想成績を、本家様4と比較してみました。
勝率の高い方を赤字で示しています。(2018年は8月19日放送分まで。本家様の成績はWebサイトより引用、ただし勝率は小数第4位を四捨五入として再計算)
これまでになかった特徴として、予想に使えるデータが少ない初期(といっても、1996年時点で4年分は貯まっているのですが)であっても、人間の予想と十分勝負できそうな勝率になっている点が挙げられます。
また、プログラムの予想結果の引き分け(あいこ)の数が、本家様と同程度にまで増えています。あいこをうまく予想に使えているようです。
(追記8/26 20:35)8/26の敗北を検証
今回の8/26の予想について、あいこの勝ち点を変えたときの予想を出してみました。
| あいこ勝ち点 | グー勝ち点予想 | チョキ勝ち点予想 | パー勝ち点予想 |
|---|---|---|---|
| 0 | 0.42401276 | 0.35985087 | 0.23581453 |
| 0.2 | 0.46947493 | 0.44375440 | 0.30598637 |
| 0.4 | 0.51194987 | 0.52623985 | 0.37821630 |
| 0.55 | 0.53150611 | 0.56800457 | 0.41944163 |
| 0.6 | 0.54474289 | 0.59718584 | 0.43474721 |
| 0.8 | 0.59671783 | 0.68444788 | 0.50430511 |
| 1.0 | 0.63791651 | 0.76162782 | 0.57367367 |
あいこ勝ち点が0の場合の結果を見ると、グー勝ち点予想が最も大きくなることから、勝ちを狙うとすれば「グー」を推していることが分かります。
(※途中でややこしくなりますが、ここで予想しているのは相手の手ではなく、自分が出すべき手です)
しかし、あいこ勝ち点を増やすとチョキが逆転します。つまり、グーを出して負けるリスクに比べて、チョキを出してあいこに持ち込んだほうが良いという判断だといえます。
相手がグーを出したので、結果的にパーを出すべきところだったのですが、あいこ勝ち点をどう変えてもパーの勝ち点予想が最大にはなりません。
今日は勝てない試合だったのでしょう。勝率75%ということは3勝する間に1回は負けるのですから、気楽に行きましょう。
今後の予定
もう一つくらいは解法を考えてみたい。いつになるのか分かりませんが。
-
図で見た方がわかりやすいですね→回帰分析 - Wikipedia ↩
-
scikit-learn: machine learning in Python — scikit-learn 0.19.2 documentation ↩
-
サザエさんとの勝負結果(年別) が毎週更新されています。 ↩