はじめに
先日、「サザエさんじゃんけん研究所」1様の「サザエさんじゃんけん白書」が話題になりました。
日曜夕方の代表的なアニメ「サザエさん」の次回予告で行われる「じゃんけん」を記録し、傾向と対策をまとめているという恐ろしい資料です。
1991年11月の開始から現在に至るまで、26年以上のじゃんけんの手が毎週分(執筆時点で1349回!)全て記録されているというから驚きです。2
さらに「サザエさんじゃんけん研究所」様では、傾向と対策を基にサザエさんと毎週じゃんけん勝負をしていて、1996年1月~2018年8月19日までの22年以上で、通算勝率70.4%を挙げているのです。3
前回、ニューラルネットワークを使ってサザエさんの手を予測する試み4を行ったところ、**1996年1月~2018年8月12日の期間で通算勝率71.51%**が得られました。
ある回の予測時には、それ以前の回の結果のみ使えるという(現実的な)制約を入れた上での結果です。
ただ、ニューラルネットワークは唯一の解ではありません。パラメータも結構色々考えないといけないのでしんどいです。
ということで、別の識別器を試してみると、意外とすんなり勝率を上げられたりして?というのが今回のテーマです。
問題設定
過去データを使ってサザエさんとじゃんけん勝負するプログラムを書きます。
「サザエさんじゃんけん研究所」様に合わせて、以下のルールで実施します。
- 1996年1月~2018年8月19日までの1136回で出す手を機械学習で決定する。
- アルゴリズムは自由。今回は**SVM(サポートベクターマシン)**を使用する。
- 各回の手の決定にあたっては、それ以前の回の手の情報だけを使うことができる。
- (※重要)当該回以降の手の情報を使ってはいけない。
- 勝率を「(勝利数)÷(勝利数+敗北数)」で計算し、「サザエさんじゃんけん研究所」様の数値と比較する。
SVMで解いてみる
SVM(サポートベクターマシン)の概要については、以下をご覧ください。
サポートベクターマシン - Wikipedia
SVMは本来2クラス分類(0か1か)をするための手法ですが、複数の識別器を使うことで多クラス(3つ以上の分類)に拡張する手法が提案されており、今回使用する機械学習ライブラリscikit-learnにも含まれています。
そのおかげで、多くの場合は2クラスか多クラスかを意識せずにSVMを使うことができます。
戦略
これも前回のニューラルネットワークのときと同じで
- サザエさんの手を予測
- 1に勝つ手を自分の手として決定する
という方針をとります。また、
- 1995年までのデータを使ってパラメータを学習し、1996年の1年間のデータを予測する。
- 1996年までのデータを使ってパラメータを学習し、1997年の1年間のデータを予測する。
- (以下略)
という感じで、1年ごとにパラメータを更新する想定とします。
選んだ特徴量
今回は今回で、相手の手の予測に必要な特徴量(素性)を色々試してみました。
結果として、以下の4次元の特徴量だけでいい感じの識別器ができたのですが、こんなに少なくて大丈夫か…?
- 放送週が各月の1週目かどうか(1次元: 1週目なら1、それ以外なら0)
- グー・チョキ・パーのそれぞれが現れていない週数(3次元)
- 前の回で現れていれば1、2回前で現れていれば2…
- 初回は便宜上 (1, 1, 1) から始めます。
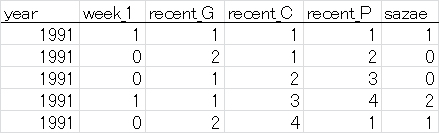
入力データは、以下の形式のテキストフォーマット(タブ区切り)で与えます。
データのフィルタリングのため、先頭に放送年の列を追加しています。
(先頭行はデータに含めません)
- 最終列はサザエさんの手で、0: グー、1: チョキ、2: パーを表す。
- 1行目は1991年11月第1週(便宜上、開始月は月の途中ですが1週目から始めます)で、サザエさんはチョキを出した。
- 2行目は1991年11月第2週で、前回はチョキ。今回はグー。
- 3行目は1991年11月第3週で、前回はグー、2回前はチョキ。今回はグー。
実際には、同様のフォーマットで1300行以上のデータが続きます。
SVMのパラメータ
SVMを実践する上で、決めなければならないことが大きく2つあります。
- カーネル関数
- ハイパーパラメータ
SVMの説明ではないので詳細は割愛しますが、どのようなカーネル関数を選ぶかによって、識別境界(0と1の境界線)の形状の自由度が変わります。あまり自由度を大きくしすぎても過学習を起こすおそれがあります。線形カーネル(伝統的?なSVM)で事足りるなら、それに越したことはありません。
色々試しましたが、今回の問題ではRBFカーネルを使っても、線形カーネルを使っても、性能に大差はありませんでした。よって、今回は線形カーネルで勝負します。
今回は、いわゆる「C-SVM」を使うことにします。よって、ハイパーパラメータ「C」を調整します。5
モデル学習時には、交差検定によってこのパラメータの値を決定して学習します。
例えば学習データをX, Y, Zの3組に分けたとき、Cの値を色々変えて
- X, Yだけを使って学習したモデルで、Zを識別する
- X, Zだけを使って学習したモデルで、Yを識別する
- Y, Zだけを使って学習したモデルで、Xを識別する
の3つを行い、全体として最も良い識別性能が得られたCの値を、本番のモデル学習に採用しようというわけです。
今回使用するscikit-learnでは、交差検定を用いたパラメータ探索が簡単にできて便利です。6
プログラム
Python 2.7とscikit-learn7を事前にインストールしてください。
scikit-learnは、pipを使うと以下のコマンドでインストールできます(numpyなどの関連パッケージも自動的にインストールされます)。
pip install scikit-learn
なお、プログラム作成には以下のドキュメントが非常に参考になりました。
学習・評価部分
# !/usr/bin/env python2.7
# -*- coding: utf-8 -*-
import numpy as np
from sklearn.svm import LinearSVC
from sklearn.model_selection import GridSearchCV
import mydata
idx_features = np.r_[1:5]
## read data
data_orig = mydata.read()
win_total = 0
draw_total = 0
lose_total = 0
for year in xrange(1996, 2019):
# 前年までのデータで学習
data_train = data_orig[data_orig[:, 0] < year]
X_train = data_train[:, idx_features]
y_train = data_train[:, -1]
# 交差検定により最適なハイパーパラメータを決定してから学習
parameters = [{'dual': [False], 'C': np.logspace(-2, -1, 10)}]
clf_cv = GridSearchCV(LinearSVC(), parameters, n_jobs = -1)
clf_cv.fit(X_train, y_train)
clf = LinearSVC(dual=False, C=clf_cv.best_estimator_.C, random_state=0)
clf.fit(X_train, y_train)
# その年のデータでテスト
data_test = data_orig[data_orig[:, 0] == year]
X_test = data_test[:, idx_features]
y_test = data_test[:, -1]
# 相手の手を予測して自分の手を決定
# 0: G, 1: C, 2: P
y_predict = clf.predict(X_test)
mychoice = (y_predict + 2) % 3
# 判定
judge = (mychoice + 3 - y_test) % 3
win = (judge == 2).sum()
draw = (judge == 0).sum()
lose = (judge == 1).sum()
win_total += win
draw_total += draw
lose_total += lose
print "{0} Win: {1:3d}, Draw: {2:3d}, Lose: {3:3d} / Avg: {4:.2f}%".format(year, win, draw, lose, float(win)/(win+lose)*100)
print "======"
print "<TOTAL> Win: {0:3d}, Draw: {1:3d}, Lose: {2:3d} / Avg: {3:.2f}%".format(win_total, draw_total, lose_total, float(win_total)/(win_total+lose_total)*100)
データ読み込み
# -*- coding: utf-8 -*-
import numpy as np
def read():
# read data
with open("input.txt", "r") as fr:
data = [[int(val) for val in l.split(None)] for l in fr]
return np.array(data, dtype=int)
データ
先程説明したフォーマットです。
元データは本家様のサイトからせっせとスクレイピングさせていただきました。m(_ _)m
1991 1 1 1 1 1
1991 0 2 1 2 0
1991 0 1 2 3 0
1991 1 1 3 4 2
1991 0 2 4 1 1
:
:
2018 0 4 2 1 0
結果
以下のように実行します。結果が出るまで1分程度お待ちください。
python train_eval.py
実行結果はこちら。2018年は8月19日放送分までです。
1996 Win: 24, Draw: 14, Lose: 12 / Avg: 66.67%
1997 Win: 29, Draw: 10, Lose: 12 / Avg: 70.73%
1998 Win: 30, Draw: 10, Lose: 12 / Avg: 71.43%
1999 Win: 25, Draw: 11, Lose: 14 / Avg: 64.10%
2000 Win: 23, Draw: 17, Lose: 11 / Avg: 67.65%
2001 Win: 23, Draw: 15, Lose: 13 / Avg: 63.89%
2002 Win: 32, Draw: 11, Lose: 7 / Avg: 82.05%
2003 Win: 24, Draw: 14, Lose: 12 / Avg: 66.67%
2004 Win: 24, Draw: 15, Lose: 10 / Avg: 70.59%
2005 Win: 23, Draw: 14, Lose: 12 / Avg: 65.71%
2006 Win: 25, Draw: 12, Lose: 13 / Avg: 65.79%
2007 Win: 23, Draw: 12, Lose: 16 / Avg: 58.97%
2008 Win: 31, Draw: 9, Lose: 11 / Avg: 73.81%
2009 Win: 29, Draw: 16, Lose: 5 / Avg: 85.29%
2010 Win: 31, Draw: 12, Lose: 5 / Avg: 86.11%
2011 Win: 34, Draw: 10, Lose: 7 / Avg: 82.93%
2012 Win: 29, Draw: 10, Lose: 10 / Avg: 74.36%
2013 Win: 30, Draw: 12, Lose: 9 / Avg: 76.92%
2014 Win: 32, Draw: 11, Lose: 8 / Avg: 80.00%
2015 Win: 34, Draw: 8, Lose: 9 / Avg: 79.07%
2016 Win: 26, Draw: 12, Lose: 11 / Avg: 70.27%
2017 Win: 32, Draw: 5, Lose: 11 / Avg: 74.42%
2018 Win: 20, Draw: 8, Lose: 5 / Avg: 80.00%
======
<TOTAL> Win: 633, Draw: 268, Lose: 235 / Avg: 72.93%
なんと勝率が**72.93%**まで上がりました。
パラメータをもっと作為的に選ぶと73%を超える場合もあったのですが、過学習の心配もあります(今後の未知データに対して性能が低下するかも?)ので、これを今回の結果としておきます。
考察など
結果について
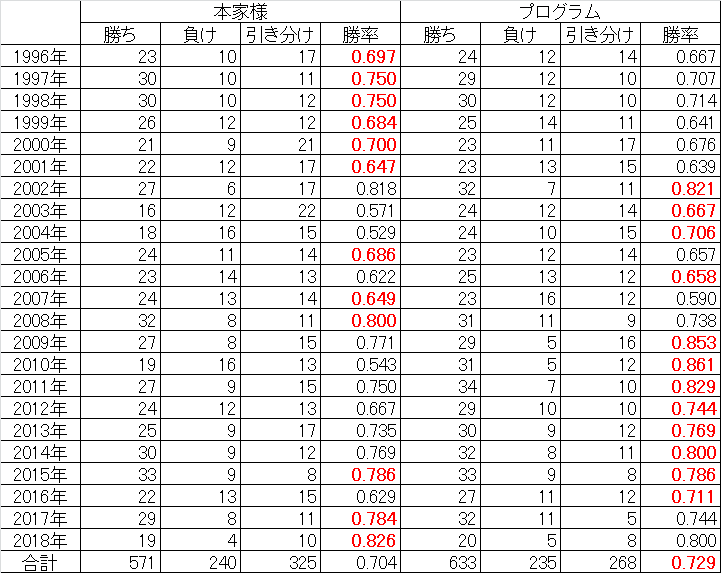
年ごとの予測成績を、本家様3と比較してみました。
勝率の高い方を赤字で示しています。(2018年は8月19日放送分まで。本家様の成績はWebサイトより引用、ただし勝率は小数第4位を四捨五入として再計算)
前回のニューラルネットワーク編でもそうでしたが、使えるデータが増えてくるごとに、プログラムの予測性能が上がっていく傾向が読み取れます。
特徴量について
- 週情報は、1~5週目の1-of-K表現よりも、1週目かどうかだけを使った方が良かった
- ただし、週情報を一切使わないと勝率70%程度に低下したので、月初めかどうかは予測に重要な特徴であるらしい
- 単に最も長期間出なかった手の情報を入れるより、それぞれの手が何週出ていないかを入れるほうが性能が良かった(前回と同じ)
- 「1回前の手」「2回前の手」の情報は、使っても使わなくても性能にあまり差がなかった。これらの情報は「グー・チョキ・パーのそれぞれが現れていない週数」の情報に含まれているからと考えられる
- 例えば「1回前がグー、2回前がチョキ」なら、グーは1、チョキは2、パーは3以上の値を取るはず
- 一般論として、識別に不要な特徴は除いておいた方が良い8ので、今回は除くことにした
戦略について
今回は、サザエさんの出す手を予測し、それに勝つ手を出す戦略を取りました。
例えば、相手の「グー」のスコアが最も高ければ、「パー」を出します。
ニューラルネットワークのときと同様に、**「最も負ける確率の低い手を出す」**戦略も試しましたが、勝率アップになりませんでした。
そのため、前回議論していた「あいこ」については、今回も特別なことをせずに普通の3クラス問題として解いています。
最後に
次回の記事では、いよいよ「あいこ」を考えた識別器作りを紹介する予定です。えっ、まだ続くの?