LU分解 in Rust!!

広島大学ITエンジニアアドベントカレンダー Advent Calendar 2019の3日目の記事です。

広島大学工学部4年生荒木勇登です！
来年から福岡でITエンジニアします！
いみこというハンドルネームでTwitterをやっていますのでそちらもご確認ください。
（https://twitter.com/es__135 ）

#LU分解とは

ある正方行列をした三角行列Lと上三角行列Uの積に分解することです。

例えば、以下のような感じです。

\begin{pmatrix} 
2 & 4 \\ 6 & 8  \end{pmatrix} = \begin{pmatrix} 2 & 0 \\ 6 & -4\\ \end{pmatrix} \times   \begin{pmatrix}  1 & 2 \\ 0 & 1\\  \end{pmatrix}

このように三角行列に分解すると何が嬉しいのかというと、三角行列では行列式は体格成分の積になるので非常にシンプルに計算することができます。
他にもさまざまな応用がありますが詳しくは参考文献をご覧ください。
具体例で学ぶ数学
https://mathwords.net/lubunkai
ウィキペディア
https://ja.wikipedia.org/wiki/LU%E5%88%86%E8%A7%A3

#実装

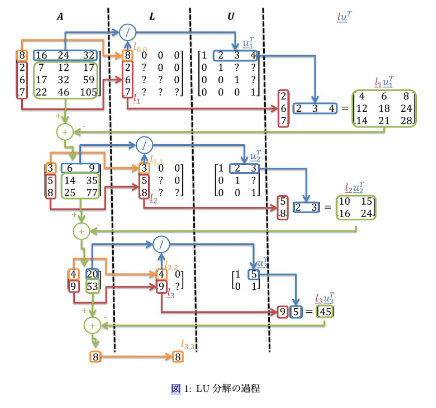
（上図は　http://www.ced.is.utsunomiya-u.ac.jp/lecture/2011/prog/p2/kadai3/no3/lu.pdf より引用）
詳しいアルゴリズムについては言葉で説明するより上の図を見ていただくのが早いのでこちらをご覧ください。

長くなりましたがLUcal関数だけ読んでいただけたらと思います。
変数名が上図の色と対応しているのでそこを確認していくとわかりやすいかもしれません。

LU.rs

ub struct Matrix {
    mat: Vec<Vec<f64>>,
    row: usize,
    col: usize
}
//LU分解の計算の本体
pub fn LU_cal(i: usize,N: usize,mut L: Matrix,mut U: Matrix,mut lu: Matrix,A: &Matrix) -> (Matrix,Matrix) {
    let n       = N - i - 1;
    let orange  = A.mat[0][0];
    L.mat[i][i] = A.mat[0][0];

    let mut red: Vec<f64> = vec![0.0;n];
    for j in 0..n {
        L.mat[j + i + 1][i] = A.mat[j + 1][0];
        red[j]              = A.mat[j + 1][0];
    }

    let mut blue: Vec<f64> = vec![0.0;n];
    for j in 0..n {
        U.mat[i][j + i + 1] = A.mat[0][j + 1] / orange;
        blue[j]             = A.mat[0][j + 1] / orange;
    }

    for j in 0..n {
        for k in 0..n {
            lu.mat[j][k] = red[j] * blue[k];
        }
    }

    let mut green = zero(n,n);
    for j in 0..n {
        green.mat[j] = vec![0.0;n];
        for k in 0..n {
            green.mat[j][k] = A.mat[j + 1][k + 1] - lu.mat[j][k];
        }
    }

    if i == N - 1 {
        (L,U)
    }else{
        //greenの行列が次のredになります
        LU_cal(i + 1,N,L,U,lu,&green)
    }
}

//正方行列かどうかの確認とLU calの呼び出し
pub fn LU(a: &Matrix) -> (Result<Matrix,String>,Result<Matrix,String>) {
    let N = a.col;
    let temp_l = zero(N,N);
    let temp_u = iden(N);
    let lu     = zero(N,N);

    let (L,U) = LU_cal(0,N,temp_l,temp_u,lu,a);
    let l:Result<Matrix,String> = match a.col == a.row {
        true  => Ok(L),
        false => Err("計算不可能です".to_string()),
    };
    let u:Result<Matrix,String> = match a.col == a.row {
        true  => Ok(U),
        false => Err("計算不可能です".to_string()),
    };
    (l,u)
}

//零行列、単位行列を作る関数の定義
//どうでも良いので無視してください

pub fn iden(n: usize) -> Matrix {
    let mut b: Vec<Vec<f64>> = Vec::new();
    for i in 0..n {
        let mut c: Vec<f64> = Vec::new();
        for j in 0..n {
            match i == j {
                true  => c.push(1.0),
                false => c.push(0.0),
            }
        }
        b.push(c);
    }
    Matrix {
        mat: b,
        row: n,
        col: n
    }
}

pub fn zero(_row: usize,_col: usize) -> Matrix {
    Matrix{
        mat: vec![vec![0.0;_row];_col],
        row: _row,
        col: _col
    }
}


fn main(){
    let _a = Matrix{
        mat: vec![vec![ 8.0,16.0,24.0,32.0],
                  vec![ 2.0, 7.0,12.0,17.0],
                  vec![ 6.0,17.0,32.0,59.0],
                  vec![ 7.0,22.0,46.0,105.0]],
        row: 4,
        col: 4
    };
    let (_b,_c) = LU(&_a);
    println!("{:?}",&_b.unwrap().mat);
    println!("{:?}",&_c.unwrap().mat);
}

(実装はこの記事を参考にさせていただきました。https://qiita.com/edo_m18/items/1d67532bed4a083cddb3)
同じアルゴリズムを再帰的に行っています。Rustではこのような場合、所有権が問題になりfor文では実装しにくいため再帰関数で実装しました。
#参考文献
具体例で学ぶ数学
https://mathwords.net/lubunkai
ウィキペディア
https://ja.wikipedia.org/wiki/LU%E5%88%86%E8%A7%A3
宇都宮大学の資料
http://www.ced.is.utsunomiya-u.ac.jp/lecture/2011/prog/p2/kadai3/no3/lu.pdf

@edo_m18 様の記事
https://qiita.com/edo_m18/items/1d67532bed4a083cddb3