概要
今作っているVRコンテンツで、3次元の最小二乗平面(参考: 最小二乗平面の求め方 - エスオーエル)を利用した、とある値を求めたくて色々と調べていたら、それを求める上で必要な連立方程式の解法として「LU分解法」なるものに行き着いたのでJSで書いてみた、というのが経緯。
数学のロジックをプログラムに落とすのにあんまり慣れてないので、特訓の意味も含めてやった感じです。
(なので全然スマートじゃないですが、とりあえず期待通りの値になったのでメモ)
ちなみに今回のプログラムは、こちらの資料(LU分解による連立方程式の解法)を参考にしました。
LU分解とは
自分のためのメモとして理解している範囲でLU分解を説明してみたいと思います。
LU分解とは、ひとつの「とある行列A」を「L」と「U」、ふたつの行列に分解して考えることで、連立方程式が解きやすくなる、というものです。
なので「LU分解」というんですね。
ちなみに「行列L」は左下三角形行列、「行列U」は右上三角形行列とも呼ばれます。
その理由は以下の配列の構造を見ると分かります。
行列L
\begin{bmatrix}
l_{00} & 0 & 0 \\
l_{10} & l_{11} & 0 \\
l_{20} & l_{21} & l_{22}
\end{bmatrix}
行列U
\begin{bmatrix}
1 & u_{01} & u_{02} \\
0 & 1 & u_{12} \\
0 & 0 & 1
\end{bmatrix}
行列Uの対角要素が1になっている以外は、右上、左下がすべて0になって三角形の形に分解されているのが分かるかと思います。
こうした行列に分けることで計算がしやすくなる、というわけです。
なぜ計算がしやすくなる?
ではなぜこういう行列に分割することで計算がやりやすくなるのか。
それは以下の例を見てください。(参考にした資料に掲載されているものです)
まず、以下の連立方程式を考えます。
\left\{
\begin{array}{ll}
8x_0 + 16x_1 + 24x_2 + 32x_3 = 160 \\
2x_0 + 7x_1 + 12x_2 + 17x_3 = 70 \\
6x_0 + 17x_1 + 32x_2 + 59x_3 = 198 \\
7x_0 + 22x_1 + 46x_2 + 105x_3 = 291
\end{array}
\right.
これを、それぞれ
A =
\begin{bmatrix}
8 & 16 & 24 & 32 \\
2 & 7 & 12 & 17 \\
6 & 17 & 32 & 59 \\
7 & 22 & 46 & 105
\end{bmatrix}
,\vec{x} =
\begin{bmatrix}
x_0 \\
x_1 \\
x_2 \\
x_3
\end{bmatrix}
,\vec{b} =
\begin{bmatrix}
160 \\
70 \\
198 \\
291
\end{bmatrix}
と置きます。すると、
A\vec{x} = \vec{b}
と置くことで、連立方程式を恒等式として表現することができるようになります。
恒等式 恒等式(こうとうしき、英: identity)とは、等式すなわち等号 (=) を含む数式であって、そこに現れるあらゆる変数がどのような値にあっても、常に等号で結ばれた左右二つの数式の "値" が等しいもののことを言う。
引用: Wikipedia
つまり、どんな値であってもこれで解くことができる、というわけですね。
そして今、Aを「L」と「U」という行列に分解することを考えているわけなので、
LU\vec{x} = \vec{b}
と置くことができます。
そしてさらにこれを
\vec{y} = U\vec{x}
と置くと、以下のように変形することができます。
\left\{
\begin{array}{ll}
L\vec{y} = \vec{b} \\
U\vec{x} = \vec{y}
\end{array}
\right.
すると、複数の連立方程式をふたつの連立方程式で導くことができるようになります。
これが「LU分解」です。(と理解してます)
LU行列の求め方
の詳細については、資料をご覧くださいw
ポイントだけを書いておくと、左上の要素および左列、上行を求め、右下の行列を$N - 1$行列として再定義することで、再帰的に行列を求めていくことができる、というものです。
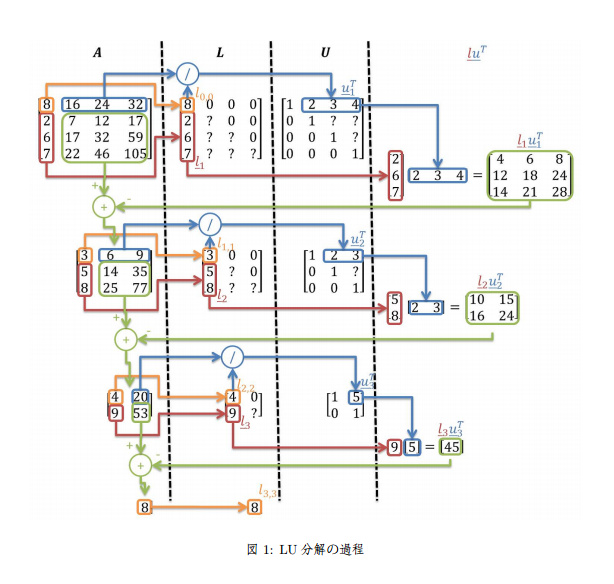
計算自体はあまり複雑ではなく、資料に解き方の図解があるので引用させていただくと以下のような感じになります。
最初見たときはなんのこっちゃ、という感じでしたが、$A, L, U$と書かれているのがそれぞれの行列を表しています。
そして一番左上の行列が元々の行列ですね。これを元に分解していく様子が書かれています。
(成分をよく見てもらうと同じ行列Aですね)
見方は、左上から始まって右に見ていく感じになります。
例えば、オレンジの部分はただ値をコピーしているだけですね。
そして赤い部分もそのままコピーしているだけです。
次の青い部分は、最初にコピーしたオレンジ色の要素で各成分を割ったものを、行列Uに入れています。
そしてそこまでの結果(赤と青)を使って、一番右の緑色の行列を求めます。
ここで求めた緑の行列は、元々の行列Aの右下の行列と同じ正方行列となります。(これを仮に$A1$としましょう)
そして$A1$行列から緑の行列を引いたものを新しい$N - 1$行列として定義します。
あとはこれを繰り返し、再帰的に求めていくことで行列$LU$の各成分が求まる、という感じです。
ちなみに例に出した行列Aを実際にLU分解すると以下の結果になります。
A =
\begin{bmatrix}
8 & 16 & 24 & 32 \\
2 & 7 & 12 & 17 \\
6 & 17 & 32 & 59 \\
7 & 22 & 46 & 105
\end{bmatrix}
,L =
\begin{bmatrix}
8 & 0 & 0 & 0 \\
2 & 3 & 0 & 0 \\
6 & 5 & 4 & 0 \\
7 & 8 & 9 & 8 \\
\end{bmatrix}
,U =
\begin{bmatrix}
1 & 2 & 3 & 4 \\
0 & 1 & 2 & 3 \\
0 & 0 & 1 & 5 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
LU分解を用いた連立方程式の解法
以上でLU分解を行った行列$LU$が求まりました。
あとはこれを使って以下の連立方程式を解くだけで答えが求まります。
\left\{
\begin{array}{ll}
L\vec{y} = \vec{b} \\
U\vec{x} = \vec{y}
\end{array}
\right.
$\vec{y}$は変数$\vec{x}$を用いて求めているように見えるので未知数のように見えますが、$L$と$\vec{b}$が既知のため求めることができます。
そうして求めた$\vec{y}$を利用して、最終的な$\vec{x}$を求める、というのが解法となります。
数学的な式や解説は元の資料をご覧ください。
あとはこれをプログラムで書くと以下のようになります。
ソースコード
(function () {
'use strict';
// とりあえず成分数は明示的に書いておく
let N = 4;
// 分解したい行列A
let matA = [
[8, 16, 24, 32],
[2, 7, 12, 17],
[6, 17, 32, 59],
[7, 22, 46, 105]
];
// 分解した下三角行列L用バッファ
let matL = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
// 分解した上三角行列U用バッファ
let matU = [
[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1],
];
// 分解後に利用するバッファ用行列
let lu = [
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
[0, 0, 0, 0],
];
let b = [
160, 70, 198, 291,
];
for (let i = 0; i < N; i++) {
let n = N - i - 1;
// l0_0成分をコピー
let l0 = matL[i][i] = matA[0][0];
// l1成分をコピー
let l1 = [];
for (let j = 0; j < n; j++) {
matL[j + i + 1][i] = l1[j] = matA[j + 1][0];
}
// →u1^T成分をコピー
let u1 = [];
for (let j = 0; j < n; j++) {
matU[i][j + i + 1] = u1[j] = matA[0][j + 1] / l0;
}
// luを求める
for (let j = 0; j < n; j++) {
for (let k = 0; k < n; k++) {
lu[j][k] = l1[j] * u1[k];
}
}
// A1を求める(n-1行列)
let A1 = [];
for (let j = 0; j < n; j++) {
A1[j] = [];
for (let k = 0; k < n; k++) {
A1[j][k] = matA[j + 1][k + 1] - lu[j][k];
}
}
// A1を改めてmatAとして再帰的に解く
matA = A1;
}
// 求めたLU行列を使って連立方程式を解く
let y = new Array(N);
for (let i = 0; i < N; i++) {
let sum = 0;
for (let k = 0; k <= i - 1; k++) {
sum += matL[i][k] * y[k];
}
y[i] = (b[i] - sum) / matL[i][i];
}
let x = new Array(N);
for (let i = N - 1; i >= 0; i--) {
let sum = 0;
for (let k = i + 1; k <= N - 1; k++) {
sum += matU[i][k] * x[k];
}
x[i] = y[i] - sum;
}
// 以上で求めた$x$の配列が、最終的に求めたい変数$x_0, x_1, x_2, x_3$それぞれの解となります。
}());
これを実行すると$\vec{x}$は
x = [4, 3, 2, 1]
となりました。
実際に代入してみると確かに正解のようです。