k-means法を使用したクラスタリングによるデータ分析（python）（【高等学校情報科 情報Ⅱ】教員研修用教材）

#はじめに

非階層型クラスタリングの手法の一つに、k-means法（k平均法）があります。
教材の「第3章 情報とデータサイエンス 後半 学習16.クラスタリングによる分類」の記述がわかりやすいので引用します。

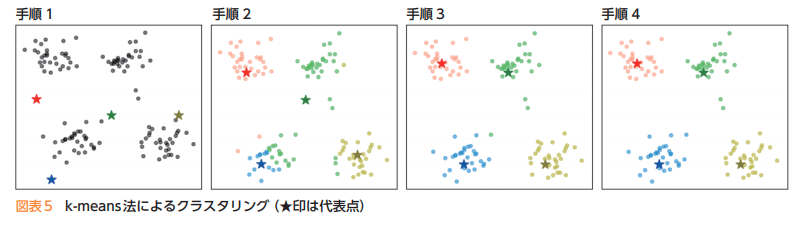
k-means法では，次の手順によってクラスタリングする。
1） あらかじめ分割するクラスタ数を決めておき，ランダムに代表点（セントロイド）を決める。
2） データと各代表点の距離を求め，最も近い代表点のクラスタに分類する。
3） クラスタごとの平均を求め，新しい代表点とする。
4） 代表点の位置が変わっていたら2に戻る。変化がなければ分類終了となる。
1）によりランダムに代表点を決めることによって，結果が大きく異なり，適切なクラスタリングとな
らない場合もある。何回か繰り返して分析をしたり，k-means++法を用いたりすることにより改善することができる。

1’）データの中からランダムに一つの代表点を選び，その点からの距離の2乗に比例した確率で残りの代表点を選ぶ。

教材のクラスタリングについての説明が書かれている箇所「第3章 情報とデータサイエンス 後半 学習16.クラスタリングによる分類」では、すでにpythonによる実装例にて解説されてあります。
今回は「第5章 情報と情報技術を活用した問題発見・解決の探究 , 巻末　活動例3．データを活用するための情報技術の活用」内で、Rで書かれている実装例をpythonに置き換えることで、k-means法を使用したクラスタリングによるデータ分析について確認していきたいと思います。

教材

高等学校情報科「情報Ⅱ」教員研修用教材(本編)：文部科学省
第5章 情報と情報技術を活用した問題発見・解決の探究 , 巻末 (PDF:4.1MB)

環境

ipython
Colaboratory - Google Colab

教材内で取り上げる箇所

活動例3 データを活用するための情報技術の活用

pythonでの実装例と結果

分析を行う前に

今回、教材ではグラフプロットの際に日本語を使っております。
そのため、あらかじめグラフプロット(matplotlib)で日本語を使用できるように設定する必要があります。

!apt-get -y install fonts-ipafont-gothic
!ls -ll /root/.cache/matplotlib/

：
-rw-r--r-- 1 root root 46443 Sep 18 20:45 fontList.json
-rw-r--r-- 1 root root 29337 Sep 18 20:25 fontlist-v310.json
drwxr-xr-x 2 root root  4096 Sep 18 20:25 tex.cache

lsコマンドの情報をもとに、古いフォントキャッシュのfontlist-v310.jsonを削除します。

# キャッシュを削除する。
!rm /root/.cache/matplotlib/fontlist-v310.json # 消すべきcache
!ls -ll /root/.cache/matplotlib/

# キャッシュを削除する。
!rm /root/.cache/matplotlib/fontlist-v310.json # 消すべきcache
!ls -ll /root/.cache/matplotlib/

ここで、google colabのランタイムのりスタートを行います。
次に、matplotlibで日本語が使えるように設定します。

import matplotlib

#日本語表示
matplotlib.rcParams['font.family'] = "IPAGothic"

前処理

「学校における教育の情報化の実態等に関する調査」として、以下のExcelデータをダウンロードします。

「都道府県別『コンピュータの設置状況』及び『インターネット接続状況』の実態（高等学校）」

教材同様に、最初にpythonで分析をする前に、Excel上でデータクリーニングを行います。
整理・整形を行ったデータは以下としました。

pc_sjis.csv

行った処理は以下のとおりです。

• 不必要なヘッダー，フッターの削除
• 不必要な項目の削除
• データをCSV形式にするため桁区切りのカンマの除去
• 項目名を作業しやすいように英字に変更
• データの各項目は，pref（都道府県別），school（学校数），student（児童生徒数），room（普通教室数），PC（学習者用PC総台数），spp（学習者用PC1台当たりの児童生徒数），prj（普通教室の大型提示装置整備率），lan（普通教室の校内LAN整備率），wlan（普通教室の無線LAN整備率）

これらにもとづいて、データを読み込みを行います。

import pandas as pd
from IPython.display import display

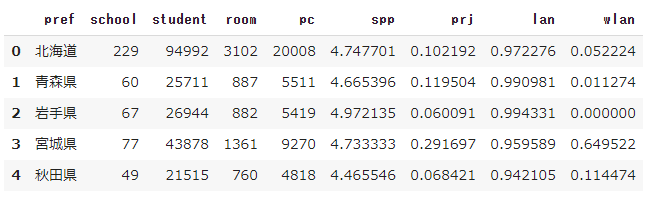
pc = pd.read_csv('/content/pc_sjis.csv', encoding='shift_jis')
display(pc.head())

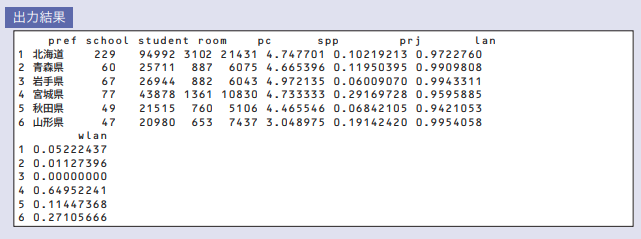
教材では、以下のようになっています。

教材では、学習者用PC総台数を読み込むべきところを教育用ＰＣ総台数が読み込んでいる誤りがあるようです。

データの分析、可視化

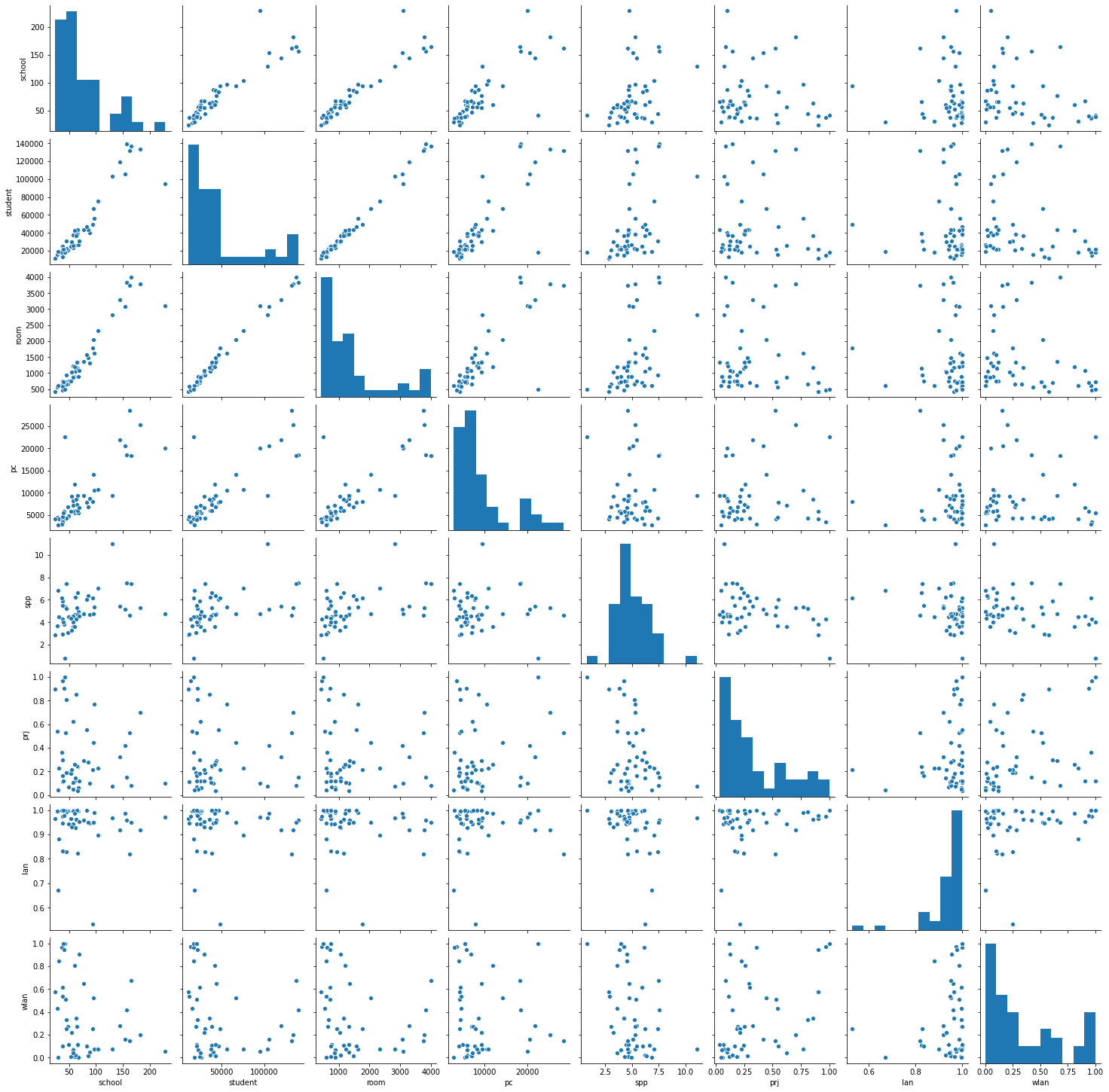
どのような傾向が読み取れるかを把握するため、まず散布図行列を表示してみます。
今回は、seabornモジュールを使ってみます。

import seaborn as sns

pg = sns.pairplot(pc)
print(type(pg))

教材より、

生徒数と教室数のように直線傾向が明確に見えるものは，「情報Ⅰ」で学んだ相関係数や単回帰分析などの対象になる。今回は，直線傾向を見るのではないので，wlan（無線LAN）とspp（PC1台当たりの生徒数）を対象に考えてみよう。

とあるのでwlan（無線LAN）とspp（PC1台当たりの生徒数）の値を取り出し、スケーリングを行う。

具体的には、標準化を行いました。

from sklearn.preprocessing import StandardScaler

# 値の抽出(wlan spp)
pc_ws = pc[['wlan', 'spp']]

# 標準化(StandardScalerを使用したやり方)
std_sc = StandardScaler()
std_sc.fit(pc_ws)
pcs = std_sc.transform(pc_ws)
pcs_df = pd.DataFrame(pcs, columns = pc_ws.columns)
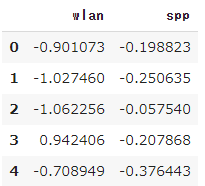
display(pcs_df.head())

扱うデータの種類が別々なので、教科書と同じように標準化を行っております。
標準化については、過去の記事が参考になります。
https://qiita.com/ereyester/items/b78b22a76a8f50006880

次にモデルの作成と分類を行います。

from sklearn.cluster import KMeans

#モデルの作成 
km = KMeans(init='random', n_clusters=2 , random_state=0)
#予測
pc_cluster = km.fit_predict(pcs_df)
cluster_df = pd.DataFrame(pc_cluster, columns=['cluster'])

# 値の抽出(pref wlan spp cluster)
pcs_cluster_df = pd.concat([pc[['pref', 'wlan', 'spp']], cluster_df], axis=1)
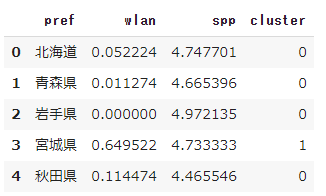
display(pcs_cluster_df.head())

結果を散布図で確認したいと思います。

import matplotlib.pyplot as plt
import numpy as np
import seaborn as sns

_, ax = plt.subplots(figsize=(5, 5), dpi=200)

sns.scatterplot(data=pcs_cluster_df, x="wlan", y="spp", hue="cluster", ax=ax)

for k, v in pcs_cluster_df.iterrows():
    ax.annotate(v['pref'],xy=(v['wlan'],v['spp']),size=5)

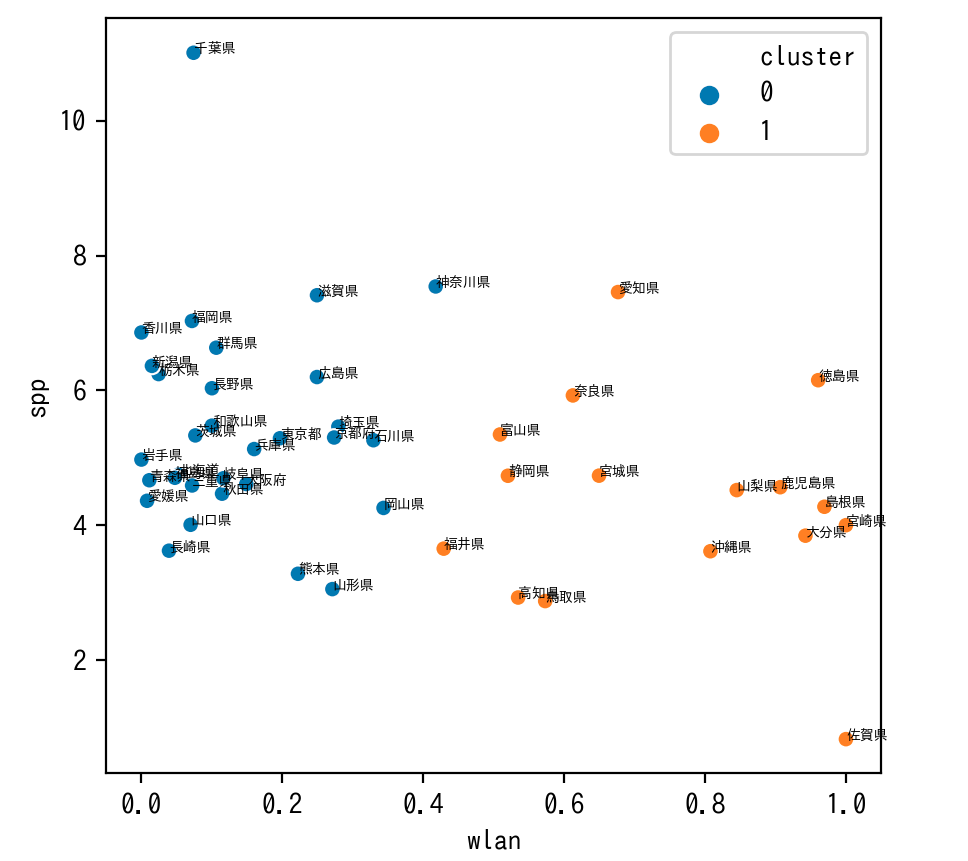
plt.show()

全体的に無線LAN(wlan)を情報をもとにして分類しているように見えます。
また、千葉県や佐賀県は群の中心から外れているように見えます。

さらに分析

次は明らかな正の相関関係が読み取れる生徒数と学習用PCの台数のグラフについて、先ほどのクラスタで色分けしてグラフをプロットしてみます。

# 値の抽出(pref student pc cluster)
pcs_cluster2_df = pd.concat([pc[['pref', 'student', 'pc']], cluster_df], axis=1)

_, ax2 = plt.subplots(figsize=(5, 5), dpi=200)

sns.scatterplot(data=pcs_cluster2_df, x="student", y="pc", hue="cluster", ax=ax2)

for k, v in pcs_cluster2_df.iterrows():
    ax2.annotate(v['pref'],xy=(v['student'],v['pc']),size=5)

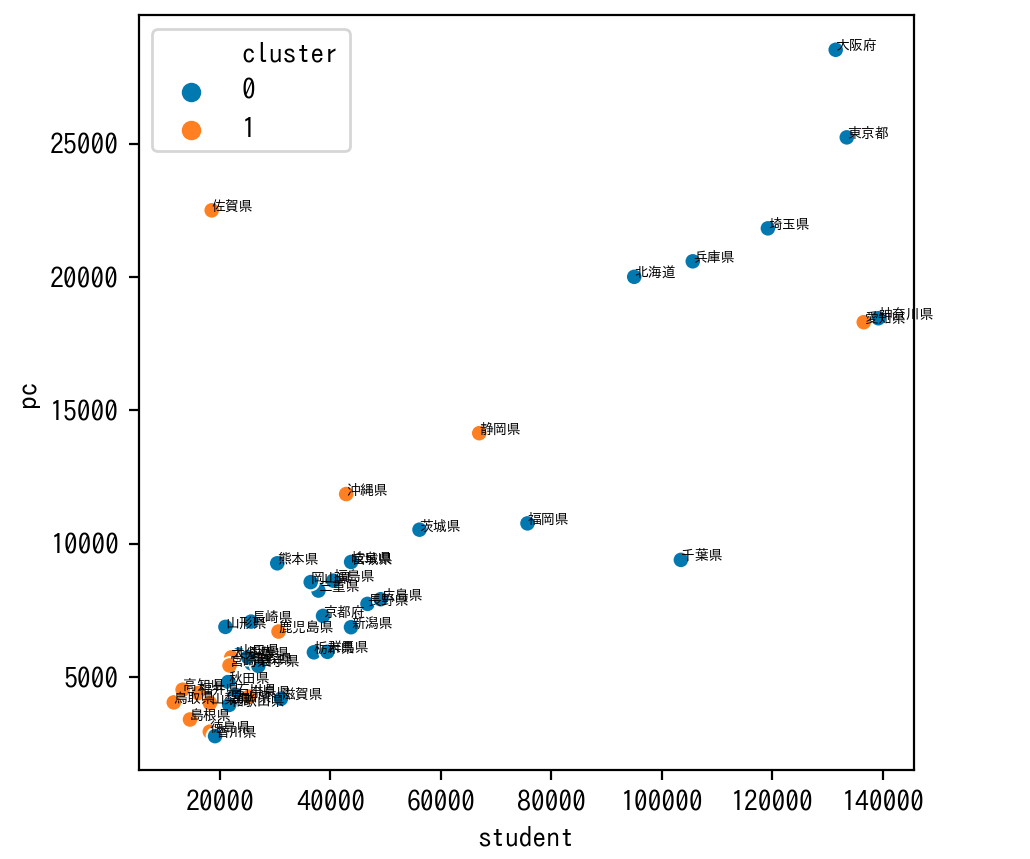
plt.show()

student（生徒数）に対するPC（学習者用PC総台数）の割合が大きいとwlan（普通教室の無線LAN整備率）の整備率の高いグループになる傾向があり、そうでないとwlan（普通教室の無線LAN整備率）の整備率の低いグループにある傾向があるようにみえます。
佐賀県はstudent（生徒数）に対するPC（学習者用PC総台数）の割合がとても大きく、逆に千葉県はstudent（生徒数）に対するPC（学習者用PC総台数）の割合がとても小さいなどの特徴が見てとれます。

ソースコード