はじめに
主成分分析とは、対象の特徴を表す多変量のデータから複数の変数をまとめて主成分(特徴量)を作成する手法です。
次元削減が行える手法であり、データの構造を見やすくしたり、機械学習の計算量を削減して計算スピードを向上させたりすることができます。
簡単に言うと、相関のある多変量のデータを、ばらつきの方向と大きさに注目してより相関の少ない関数により、データを表現する手法です。
今回は、文部科学省のページで公開されている情報Ⅱの教員研修教材内の「主成分分析と次元削減」で取り上げられているものをpythonで実装しつつ、仕組みを確認していけたらと思います。
教材
高等学校情報科「情報Ⅱ」教員研修用教材(本編):文部科学省
[第3章 情報とデータサイエンス 前半 (PDF:8.9MB)](https://www.mext.go.jp/content/20200702-mxt_jogai01-000007843_004.pdf" 第3章 情報とデータサイエンス 前半 (PDF:8.9MB)")
環境
- ipython
- Colaboratory - Google Colab
今回やりたいこと
主成分分析に関して、なるべく数式等を使わずに主成分分析に関して概要を説明した後、
学習14 主成分分析と次元削減:「4. Rで体力測定のデータを分析してみよう」
のRで書かれたソースコードをpythonで実装しつつ、仕組みを見ていきたいと思います。
主成分分析
主成分分析の概要(教材より)
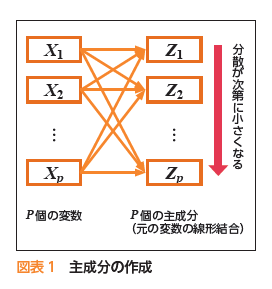
主成分分析(PCA)の仕組みを簡潔に説明すると、変数の間の共分散や相関の強い変数同士をまとめて、個々の対象の違いを最も大きくするような主成分と呼ばれる新しい特徴量(変数)を作成することである。
図のように、p個の変数 $ (X_1 , X_2 , \cdots , X_p) $ から、情報を損失することなく線形結合(重み付きの合計)によって、p個のお互いに独立な合計変数を主成分$ (Z_1 , Z_2 , \cdots , Z_p) $として作成する。
主成分は、分散が最も大きくなるような順番で作成され、下位の主成分になるに従って、対象間で主成分の値(主成分得点)の変動(分散)が小さくなる。
すなわち、寄与の小さい下位の方の主成分を捨て、上位の主成分のみ採用することで、元の個数pより少ない数で、対象の特徴をプロファイルすることが可能になり、それを次元削減(次元縮約)という。
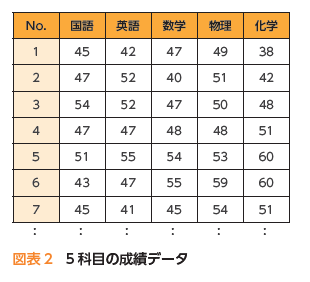
以下の簡単な例(5教科の試験に関する成績データ)を考える。
各教科の係数を一般化して、a,b,c,d,eとして作成される合成変数を考える。
合計変数=a×国語+b×英語+c×数学+d×物理+e×化学
a,b,c,d,eにいろいろな数値を与えると、単純な合計得点以外の合計得点をいろいろ作成することができる。
主成分分析で作成する主成分とは、係数a,b,c,d,eを50人の生徒の合計変数の値**(主成分得点)**が最もばらつくように、つまり、分散が最大となるように決定される1つの変数である。
ばらつきが大きいことがその変数の情報量の大きさに対応する。
最初に求められる主成分を第1主成分といい、次に求められる第2主成分は、第1成分と独立である(無相関)という条件の下で、分散が最大になるように求められ、お互いに相関しない、情報が重複しない特徴量となる。
主成分分析における標準化の議論
教材より
合成変数を作成する場合、二つの立場がある。
- ① 5科目の得点のレベル(位置)をそろえる(平均を同じにする,平均からの偏差にする)。
- ②5科目の得点のレベル(位置)とばらつきの大きさの双方をそろえる(平均と標準偏差を同じにする,基準化(標準化)する,または,偏差値にする)。
単位が異なる複数の変数を扱う場合は,②の基準化を行い,単位をそろえる必要がある。単位が同じ場合は,①と②の双方の立場で分析が可能である。①では,各変数の分散の大きさを考慮した係数が求まり,②では,各変数の分散の違いを無視した係数が求まる。
①②のどちらを採用すべきかという議論については、以下でまとめてくださっている情報が詳しいです。
- 主成分分析で標準化(標準偏差で割る)するのが必ずしもいいとは限らない
- それどころか標準偏差で割ることの悪影響もある
- 標準化すべきかどうかは、どこで主成分分析を使うか(可視化として使うのか、パイプラインとして使うのか)によっても異なるからそこをちゃんと考えましょう
今回分析するデータ
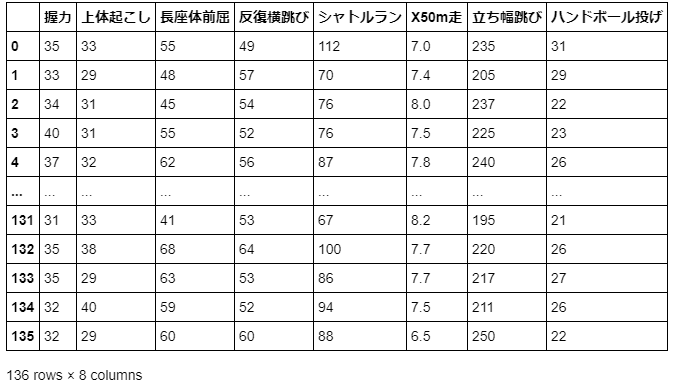
体力測定のデータ(握力、上体起こしなど)から、項目を抽出して主成分分析を行います。
こちらで作成した前処理済みの以下のデータを使用したいと思います。
python:実装例と結果
python:実装例(データの取り込み)
import numpy as np
import pandas as pd
import urllib.request
import matplotlib.pyplot as plt
import sklearn #機械学習のライブラリ
from sklearn.decomposition import PCA #主成分分析器
from sklearn.preprocessing import StandardScaler
from IPython.display import display
high_male2 = pd.read_csv('/content/high_male2.csv')
high_male3 = high_male2[['握力', '上体起こし', '長座体前屈', '反復横跳び', 'シャトルラン', 'X50m走', '立ち幅跳び', 'ハンドボール投げ']]
display(high_male3)
今回は、scikit-learnモジュールを使用した方法と使用しない方法の二種類を実装したいと思います。
scikit-learnモジュールを使用した方法では、sklearn.decomposition.PCAとsklearn.preprocessing.StandardScalerを使用し、
scikit-learnモジュールを使用しない方法では、numpyとpandasで自前で処理を実装する形になります。
python:出力結果(データの取り込み)
今回は、pandas.DataFrameを積極的に使用して、実装を進めたいと思います。
python:実装例(scikit-learn使用版PCA)
# 行列の標準化
# 標準化(StandardScalerを使用したやり方)
std_sc = StandardScaler()
std_sc.fit(high_male3)
std_data = std_sc.transform(high_male3)
std_data_df = pd.DataFrame(std_data, columns = high_male3.columns)
display(std_data_df)
# 主成分分析の実行
pca = PCA()
pca.fit(std_data_df)
# データを主成分空間に写像
pca_cor = pca.transform(std_data_df)
# print(pca.get_covariance()) # 分散共分散行列
# 固有ベクトルのマトリックス表示
eig_vec = pd.DataFrame(pca.components_.T, index = high_male3.columns, \
columns = ["PC{}".format(x + 1) for x in range(len(std_data_df.columns))])
display(eig_vec)
# 固有値
eig = pd.DataFrame(pca.explained_variance_, index=["PC{}".format(x + 1) for x in range(len(std_data_df.columns))], columns=['固有値']).T
display(eig)
# Rによるソースコードだと、固有値(分散)ではなく標準偏差を求めている。
# 主成分の標準偏差
dv = np.sqrt(eig)
dv = dv.rename(index = {'固有値':'主成分の標準偏差'})
display(dv)
# 寄与率
ev = pd.DataFrame(pca.explained_variance_ratio_, index=["PC{}".format(x + 1) for x in range(len(std_data_df.columns))], columns=['寄与率']).T
display(ev)
# 累積寄与率
t_ev = pd.DataFrame(pca.explained_variance_ratio_.cumsum(), index=["PC{}".format(x + 1) for x in range(len(std_data_df.columns))], columns=['累積寄与率']).T
display(t_ev)
# 主成分得点
print('主成分得点')
cor = pd.DataFrame(pca_cor, columns=["PC{}".format(x + 1) for x in range(len(std_data_df.columns))])
display(cor)
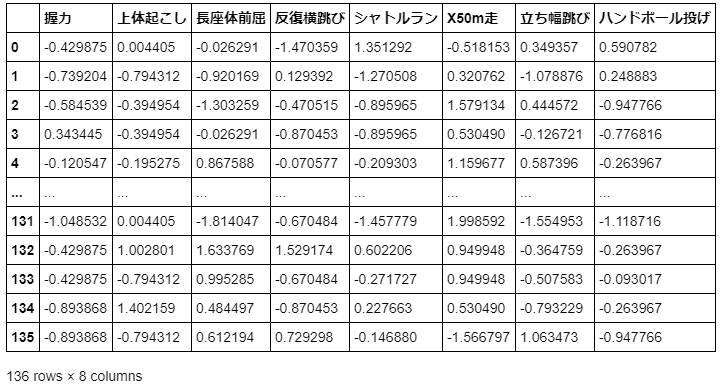
まず、sklearn.preprocessing.StandardScalerを使用して、データの標準化を行っています。
標準化により、平均0,分散1のデータに変換しております。
標準化を行ったデータに対してsklearn.decomposition.PCAを使用して、主成分分析を行っております。
主成分分析では、固有ベクトル、固有値、寄与率、主成分得点の結果を確認できるようにしております。
python:出力結果(scikit-learn使用版PCA)
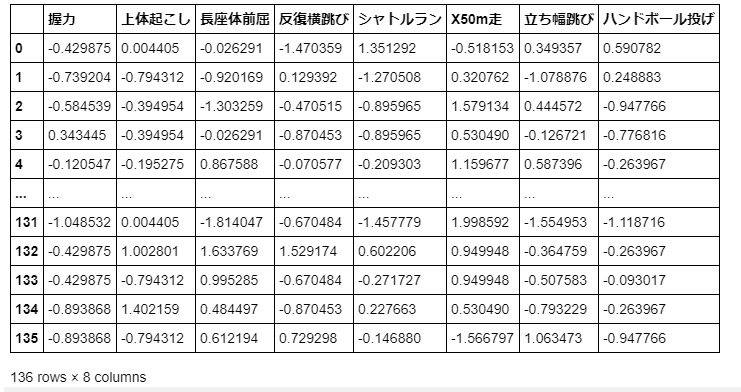
標準化されたデータ
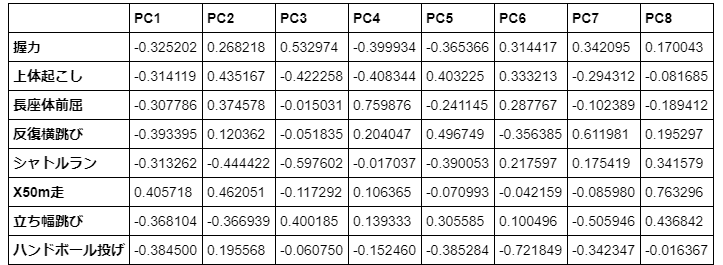
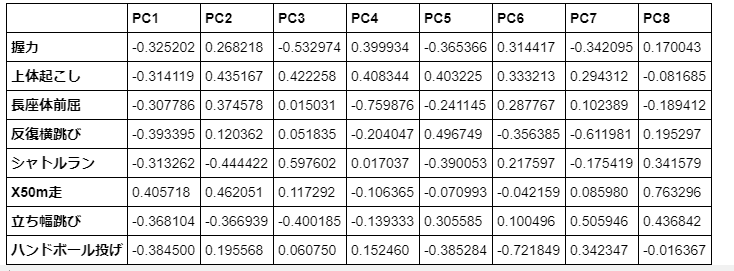
固有ベクトルの結果(PC1:第1主成分 PC2:第2主成分 ....)
固有値の結果
主成分の標準偏差(固有値を標準偏差の値にしたもの)
寄与率
累積寄与率
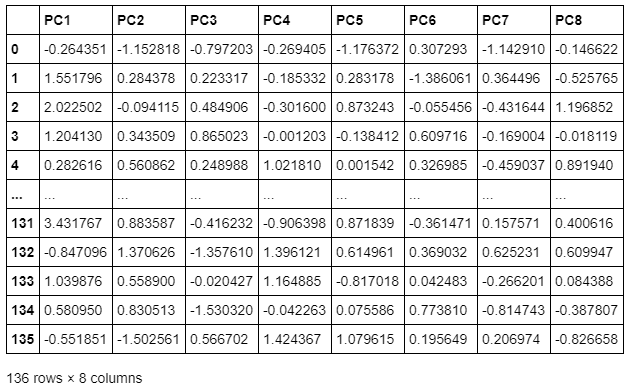
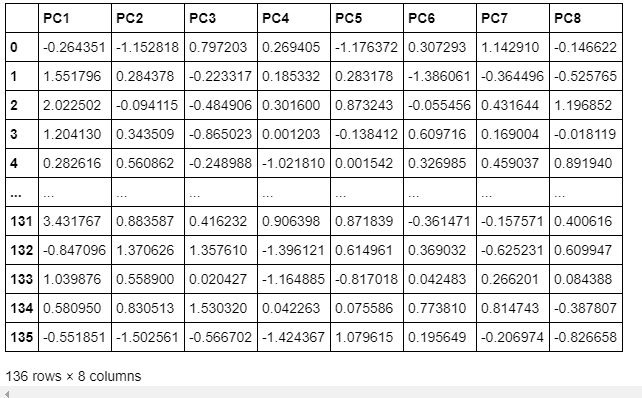
主成分得点
結果より
これらの結果からわかるのは、Rでの出力結果とほとんど変わらないことが示された。
ここで主成分得点と固有ベクトルと標準化されたデータの関係は以下の関係になっている。
主成分得点 = 固有ベクトル(握力)×標準化後握力値+固有ベクトル(上体起こし)×標準化後上体起こし値+…+固有ベクトル(ハンドボール投げ)×標準化後ハンドボール投げ値
教材では次元削減する際の基準が書かれている。
- 累積寄与率:目安は累積寄与率が70%から80%になるくらいまで採用する。
- 固有値(分散)が1以上(カイザー基準):固有値が1より大きい主成分を採用(相関行列を分析した場合=今回の場合)、寄与率が(1/変数の数)×100(%)以上になる主成分まで採用(共分散行列を分析した場合)する。
- スクリープロット:固有値(分散)を大きい順に左から折れ線グラフ(スクリープロット)に対して、分散の減少量が小さくなる(なだらかな減少になる)前までの主成分を採用する。
python:実装例(scikit-learn未使用版PCA)
# 標準化(StandardScalerを使用しないやり方)
# default:axis = 0(列方向適用)
std_data_df_noskl = (high_male3 - high_male3.mean()) / high_male3.std(ddof = 0)
display(std_data_df_noskl)
# 共分散行列
cov_vec = np.cov(std_data_df_noskl.T, bias = 0)
# 固有値と固有ベクトルを求める
# np.linalg.svd:特異値分解
# np.linalg.eig:固有値分解
# ここでは、特異値分解を選択
eig_vec_noskl_l, eig_noskl_l, _ = np.linalg.svd(cov_vec)
# 主成分得点
pca_cor_noskl = np.dot(std_data_df_noskl, eig_vec_noskl_l)
# display(cor_noskl)
# 固有値ベクトルのマトリックス表示
eig_vec_noskl = pd.DataFrame(eig_vec_noskl_l, index = high_male3.columns, \
columns = ["PC{}".format(x + 1) for x in range(len(std_data_df_noskl.columns))])
display(eig_vec_noskl)
# 固有値
eig_noskl = pd.DataFrame(eig_noskl_l, index=["PC{}".format(x + 1) for x in range(len(std_data_df_noskl.columns))], columns=['固有値']).T
display(eig_noskl)
# Rによるソースコードだと、固有値(分散)ではなく標準偏差を求めている。
# 主成分の標準偏差
dv_noskl = np.sqrt(eig_noskl)
dv_noskl = dv_noskl.rename(index = {'固有値':'主成分の標準偏差'})
display(dv_noskl)
# 寄与率
ev_noskl_l = eig_noskl_l / eig_noskl_l.sum()
ev_noskl = pd.DataFrame(ev_noskl_l, index=["PC{}".format(x + 1) for x in range(len(std_data_df_noskl.columns))], columns=['寄与率']).T
display(ev_noskl)
# 累積寄与率
t_ev_noskl = pd.DataFrame(ev_noskl_l.cumsum(), index=["PC{}".format(x + 1) for x in range(len(std_data_df_noskl.columns))], columns=['累積寄与率']).T
display(t_ev_noskl)
# 主成分得点
print('主成分得点')
cor = pd.DataFrame(pca_cor_noskl, columns=["PC{}".format(x + 1) for x in range(len(std_data_df_noskl.columns))])
display(cor)
まず、標準化を行っており、
標準化の式は、以下のようになります。
X_{i,j}^{(std)} ← \frac{x_{i,j} - \mu}{\sigma}
\mu:\frac{1}{n}\sum_{i=1}^{n} X_{i,j}
\sigma:\sqrt{\frac{1}{n}\sum_{i=1}^{n} (X_{i,j} - \mu)^2 }
{\boldsymbol{X}}=
\begin{pmatrix}
X_{1,1}^{(std)} & \cdots & X_{135,1}^{(std)} \\
\vdots & \ddots & \vdots \\
X_{1,8}^{(std)} & \cdots & X_{135,8}^{(std)}
\end{pmatrix}
ここでは、x=1,…,135=N, j=1,…,8
今回のpythonコードでは、自由度:0で標準偏差を算出しています。
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.std.html
pandas.DataFrame.stdでは、ddofint, default 1であり、引数の指定が無いと自由度1の不偏分散による標準偏差を使用することになること注意する必要があります。
ちなみに、
https://numpy.org/doc/stable/reference/generated/numpy.std.html
numpy.stdのddof int, optional default ddof is zeroとなっており、自由度0であり同様に、
https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.StandardScaler.html
sklearn.preprocessing.StandardScalerの計算中に使用する標準偏差は、ddof=0となっていることに注意が必要です。
次に標準化されたデータに対して分散共分散行列(自己共分散行列)の式は
E[\boldsymbol{X}]=0
より、
cov({\boldsymbol{X,X}})=E[\boldsymbol{X^TX}]-E[{\boldsymbol{X}}]^TE[{\boldsymbol{X}}]=E[\boldsymbol{X^TX}]=\frac{1}{N-1}\boldsymbol{X^TX}
cov({\boldsymbol{X,X}})=\Sigma
とすると、
$U$:$135\times 135$の直交行列
$S$: $135\times 8$の実対角行列(成分は非負)
$V_{svd}$: $8 \times 8$の直交行列
\boldsymbol{X}=U S {V^T_{svd}}
\boldsymbol{X^TX}=[U S {V^T_{svd}}]^T[U S {V^T_{svd}}]=V_{svd} S^T SV^T_{svd}
\Sigma=\frac{V_{svd} S^T SV^T_{svd}}{N-1}
$S^2$:固有値を対角成分に並べたもの
$V_{svd}$:$\boldsymbol{X^TX}$の固有ベクトル
特異値分解については、下記の記事が詳しいです。
主成分分析と特異値分解の関連については、下記の記事が詳しいです。
https://qiita.com/horiem/items/71380db4b659fb9307b4
https://qiita.com/sakami/items/50b8485159312573e3c7
固有値分解と特異値分解のどちらを使うかは以下の観点で、特異値分解を選択した。
Returns: w:... The eigenvalues are not necessarily ordered. とありnumpy.linalg.eigは、固有値は必ずしも順序付けされないので、固有値の大きい順に、PC1 PC2 ...と順序付けしたいので、順序付けの操作が必要になります。
Returns: Vector(s) with the singular values, within each vector sorted in descending order. とあり、降順に並び替えられたものが得られるので、こっちのほうが楽。
python:出力結果(scikit-learn未使用版PCA)
標準化されたデータ
固有ベクトルの結果(PC1:第1主成分 PC2:第2主成分 ....)
固有値の結果
主成分の標準偏差(固有値を標準偏差の値にしたもの)
寄与率
累積寄与率
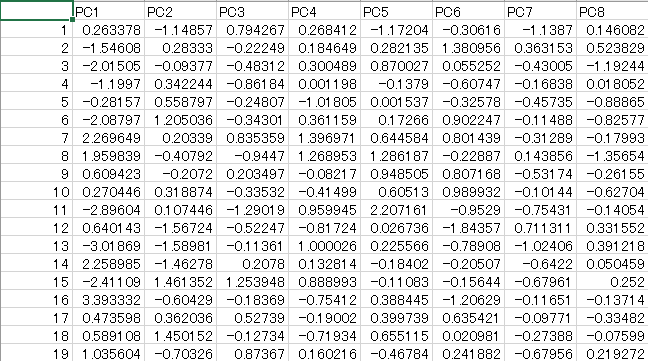
主成分得点
R:[参考]実装例と結果(教材より)
R:実装例
身長,体重,座高を除き,握力からハンドボール投げまでの8 変数を使った主成分分析
相関行列
データセット( 第4 列から第11 列) のインポート
high_male2 <- read.csv("high_male2.csv")
high_male3 <- high_male2[c(4:11)]
相関行列に基づく主成分分析prcomp の実行
(res2 <- prcomp(high_male3, scale=T))
summary(res2)
pc <- res2$x
主成分得点のファイルへの掃き出し
write.csv(pc, file = "pca_cor.csv")
prcomp()の引数scale=Tは、scale=Trueを示しており
これは、データの相関行列を用いた主成分分析を行うことを指定するパラメータであり、
今回扱う事象に関しては、実質的に標準化を行ったデータに対して主成分分析を行ったものと
等価になると予想されます。
R:出力結果
Standard deviations (1, .., p=8):
[1] 1.9677462 0.9524611 0.9096410 0.8553785 0.7327083 0.6857621 0.6399714
[8] 0.4949534
Rotation (n x k) = (8 x 8):
PC1 PC2 PC3 PC4 PC5
握力 0.3252018 0.2682176 -0.53297421 0.39993408 -0.3653663
上体起こし 0.3141190 0.4351668 0.42225757 0.40834395 0.4032249
長座体前屈 0.3077864 0.3745785 0.01503113 -0.75987597 -0.2411453
反復横跳び 0.3933948 0.1203619 0.05183489 -0.20404673 0.4967487
シャトルラン 0.3132617 -0.4444223 0.59760197 0.01703693 -0.3900527
X50m走 -0.4057185 0.4620511 0.11729178 -0.10636452 -0.0709927
立ち幅跳び 0.3681042 -0.3669386 -0.40018514 -0.13933339 0.3055848
ハンドボール投げ 0.3844997 0.1955680 0.06075045 0.15245958 -0.3852838
PC6 PC7 PC8
握力 -0.31441687 0.34209544 -0.17004275
上体起こし -0.33321281 -0.29431157 0.08168542
長座体前屈 -0.28776668 -0.10238851 0.18941208
反復横跳び 0.35638527 0.61198108 -0.19529718
シャトルラン -0.21759749 0.17541898 -0.34157859
X50m走 0.04215936 -0.08597965 -0.76329592
立ち幅跳び -0.10049579 -0.50594605 -0.43684157
ハンドボール投げ 0.72184877 -0.34234695 0.01636705
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.968 0.9525 0.9096 0.85538 0.73271 0.68576 0.6400
Proportion of Variance 0.484 0.1134 0.1034 0.09146 0.06711 0.05878 0.0512
Cumulative Proportion 0.484 0.5974 0.7008 0.79229 0.85940 0.91818 0.9694
PC8
Standard deviation 0.49495
Proportion of Variance 0.03062
Cumulative Proportion 1.00000
pca_cor.csvに関しては、以下のように出力されます。
ソースコード
python版
https://gist.github.com/ereyester/3c2173eb61cbcd64b61f23b3d4d6480c
R版
https://gist.github.com/ereyester/cd309a9ab46c37a3f594963d1ad55495