1. はじめに
この記事は、楕円曲線暗号の数学的な基礎を中心に解説する。
楕円曲線暗号はRSAと並び現在使われている暗号方式である。RSA暗号が素因数分解の困難さを根拠に置いている一方で、楕円曲線暗号は離散対数問題の困難さを根拠においている。
楕円曲線暗号を理解するには、
- 楕円曲線とは何か
- 点の加算と2倍算
- 有限体上での振る舞い
- スカラー倍算と離散対数問題
といった数学的な仕組みを押さえておく必要がある。
本記事では、それらの数学的背景を図と数式を使いながら丁寧に説明する。
後編では、
- 楕円曲線鍵共有(ECDH)
- 楕円曲線署名(ECDSA)
の Python 実装を説明する。
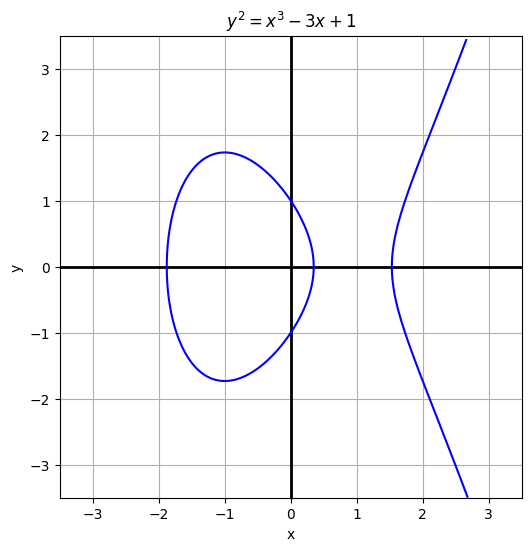
2. 楕円曲線とはなにか?
楕円曲線という名前から、幾何学の楕円(下記の図2-1)を連想しがちだが、楕円曲線はそれとはまったくの異なるものである。
楕円曲線とは、数学的には次のような形の式で表される曲線のことを指す。
$$
y^{2} = x^{3} + ax + b
$$
ここで $a, b$ は曲線を決めるパラメータである。このパラメータを変えると、様々な形をした楕円曲線を作ることができる。
ただし、すべての $a, b$ が使えるわけではなく、次の判別式を満たす $a, b$ である必要がある。
$$
4a^{3} + 27b^{2} \ne 0
$$
楕円曲線暗号では、この曲線を単なる図形としてではなく、有限体上で扱う。そのため、$x$ や $y$ の値を整数 $p$ で割ったあまりに限定し、その中で曲線上の点を定義する。
3. 楕円曲線上での加法
楕円曲線上の特徴として、曲線上の点どうしの加算を定義できるという点がある。
3.1. 点の加法の定義
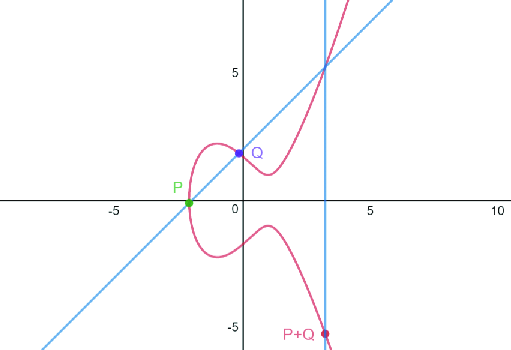
曲線上の2点 $P、 Q$ を取る。
3.1.1. P ≠ Q のとき
$P、 Q$ を通る直線を引くと、その直線はもう1点楕円曲線と交わる。これを $R$ とする。その点を $x$ 軸上に対照的な点を取った結果を $P + Q$ とする。つまり
$$
P + Q = -R
$$
と定義する。
3.1.2. P = Q のとき
$P \ne Q$ のときは2点を通る直線が曲線と3回目に交わる点を使って加法を定義した。
$P = Q$ のときは、2点を通る直線を引くことができない。
$\longrightarrow$ そこで代わりに 曲線の接戦 を用いる。
点 $P$ を通る接戦を引くと、接戦は曲線ともう一点だけ交わる。この点を $R$ とすると、加法の定義は先ほどと同じで、
$$
2P = P + P = -R
$$
となる。
3.1.3. 逆元と単位元 O(無限遠点)
楕円曲線上での加法を考えるとき、もし
$$
P \ne Q, \quad P = (x_{p}, y_{p}), \quad Q = (x_{q}, y_{q})
$$
で、$x_{p} = x_{q}$ が成り立つとき、2点を結ぶ直線は楕円曲線と3つ目の異なる点で交わらない。
この場合は、直線を無限に伸ばした先で曲線と交わると考え、その点を無限遠点と呼び、$$O_{\infty}$$ とあらわす。
楕円曲線での加法では、この無限遠点を単位元として扱い、
$$
P + O_{\infty} = P
$$
という式が成り立つ。(単位元は加算における 0 と同じように、加えても結果を変えない点である)
3.2. 加法公式
前節では、加算を直線を引いて得られた交点を、$x$ 軸に対照的に反転をするというルールで定義をした。
ここでは、このルールをコンピュータで計算できるよう、実際の座標 $(x, y)$ を使った具体的な加法公式について説明する。
2点 $P = (x_p, y_p), \ Q = (x_q, y_q)$ の加算について考える。
3.2.1. P ≠ Q のとき
点 $P, Q$ を通る直線は定義より、次のようになる。
\begin{align}
y = s(x - x_p) + y_p \ , \quad s = \frac{y_q-y_p}{x_q-x_p}
\end{align}
ここで、$s$ は直線の傾きである。
この直線と楕円曲線の交点を計算することで、3番目の点 $R$ を得ることができる。計算した結果、点 $R$ の座標は次のようになる。
\begin{align}
(x_r, y_r) &= (s^2 - x_p - x_q, \ s(x_p-x_r)-y_p) \\ s &= \frac{y_q-y_p}{x_q-x_p}
\end{align}
3.2.2. P = Q のとき
$P = Q$ のときは点 $P$ における接戦を考える必要がある。
楕円曲線の方程式 $$y^2=x^3+ax+b$$ について微分をすると、
$$
2y,\frac{dy}{dx} = 3x^{2} + a
$$
が得られる。これより、点 $P$ における接戦の傾き $s$ は、
$$
s = \frac{3x_p^{2} + a}{2y_p}
$$
となる。この接戦を用いて前節と同様に交点を計算すると、点
$R = (x_r, y_r)$ は次の式で与えられる。
\begin{aligned}
(x_r, y_r) &= (s^{2} - 2x_p, \ s(x_p - x_r) - y_p) \\[4pt]
s &= \frac{3x_p^{2} + a}{2y_p}
\end{aligned}
したがって、倍算 $2P = P + P$ の結果は次のようになる。
$$
2P = (x_r, y_r)
$$
3.3. 加法公式まとめ
2点 $P=(x_p, y_p), \quad Q=(x_q, y_q)$ を加算して、$R = (x_r, y_r)$ を得ることを考える。
| 傾き $s$ | $x_r$ | $y_r$ | |
|---|---|---|---|
| $P \ne Q$ | $\dfrac{y_q - y_p}{x_q - x_p}$ | $s^2-x_p-x_q$ | $s(x_p-x_r)-y_p$ |
| $P = Q$ | $\dfrac{3x_{p}^{2}+a}{2y_p}$ | $s^2-2x_{p}$ | $s(x_p-x_r) - y_p$ |
4. 有限体上での楕円曲線
ここまでは 2 章で楕円曲線そのものを説明し、3 章では楕円曲線上の加算について述べた。
楕円曲線暗号で実際に利用する楕円曲線は、有限体 $\mathbb{F}_p$ 上のものである。有限体では、座標や加算の結果に対して素数 $p$ で余りを取る必要がある。
3 章で導いた加算公式(傾き $s$ や $x_r, y_r$ の計算式)は、有限体上でもそのまま成立する。そのため、これらの式を用いて計算した結果について、各値を素数 $p$ で余りを取ればよい。
ただし、有限体では通常の意味での割り算は定義できないため、$\mathbb{F}_p$ における逆元を用いて計算する点だけが異なる。
4.1. なぜ有限体が必要なのか?
なぜわざわざ素数 $p$ で割ったあまりを取るのだろうか。
実数のままでは楕円曲線上の点が無限に存在し、座標も連続的である。
そのため、のちに述べる離散対数問題($P = kG$ の $k$ を求める問題)の答えを推測できるようになってしまう。
これを有限体で考える(=計算結果を素数 $p$ で割る)ことで、点の集合は離散的になり、値が連続的につながらなくなるため、$k$ を推測することが極めて困難になる。
また、$p$ で余りを取ることで、すべての計算結果が
$$
0, 1, 2, \dots, p - 1
$$
の範囲内に収まる。
このようにして、楕円曲線を有限体に移すことで、点が離散的になり、計算の振る舞いも暗号として扱いやすい形になる。
4.2. 有限体上の点集合
有限体 $\mathbb{F}_p$ 上では、楕円曲線の点集合を次のように定義する。
E(\mathbb{F}_{p}) = \{ (x, y) \in \mathbb{F}_{p}^2 \ | \ y^2 \equiv x^3 + ax + b \pmod{p}) \} \cup \ \{ O_{\infty} \}
この集合に対して 3 章で説明した加算を “mod $p$” で適用すると、楕円曲線上の点どうしの加算が有限体の範囲内で完結する。
5. スカラー倍算と安全性の根拠
4章までで定義した加算を何度も繰り返す操作が、楕円曲線暗号の全ての基本となる。
楕円曲線暗号で重要なのは、スカラー倍算 ($kG$) は高速に計算できるが、その逆から $k$ を求めるというのは難しいという点にある。
ここではそのスカラー倍算と $k$ を求める計算(=離散対数問題)について説明する。
5.1. スカラー倍算とは??
楕円曲線上の点 $G$ と、整数 $k$ があるとき、$G$ を $k$ 回自分自身に足す操作をスカラー倍算と呼び、$kG$ と書く。
$$
kG = \underbrace{G + G + \cdots + G}_{k \ 回 \phantom{}}
$$
これは3章で定義した点の加算($P + Q$) と点の2倍算($2P$)を組み合わせることで、非常に高速に計算できる。($10G = 2(2(2G)) + 2G$)
5.2. 楕円曲線離散対数問題(ECDLP)
スカラー倍算 $kG$ が高速に計算できる一方で、その逆
$$
P = kG
$$
が与えられたときに $P$ から $k$ を求めるという問題は、有限体上の楕円曲線では極めて難しいことが知られている。この問題を楕円曲線離散対数問題と呼ばれている。
実際、256bit の $k$ に対して $k$ を総当たりで求めようとすると、
$$
2^{256} \approx 10^{77}
$$
程度あるので、現実的には計算が不可能である。この困難さを前提として、のちに説明する鍵共有(ECDH)や署名(ECDSA)などがある。
6. 参考資料
[1]. Pythonで学ぶ暗号理論