今回は(何をどう解釈してどう実装したかすぐ忘れるので)自身の忘備録も兼ねて、物理ベースレンダリング (Physically Based Rendering: PBR) の取り組みについて書こうと思う。これまでの記事とオーバーラップする部分もあるのはご愛嬌。
物理ベースレンダリング(以後PBRと表記)は色々なサイトや書籍で説明されている。なので詳しいことや正確なことはそちらを参考にしていただきたい。この記事は自分なりにPBRを解釈し、それをどうプログラミングに落とし込んだかを書くので間違いも多く含まれている可能性が高い。その辺はご容赦願いたい。私が参考にした情報のいくつかを列挙する。
(Webサイト)
- URL1: 物理ベースレンダリング入門 その① - 物理ベースレンダリングとは?
- URL2: 物理ベースレンダリング -基礎編-
- URL3: 物理ベースレンダリングを柔らかく説明してみる(1)
- URL4: memoRANDOM 双方向(反射率|透過率|散乱)分布関数 (B(R|T|S)DF
(書籍)
1. 理論編
実装の前にPBRの理論面について確認しておこう。
-1. 物体に衝突した時の光の挙動
まず最初に、PBRで最も重要なことは「エネルギー保存則」である。ある物体表面に入射した光はあとで説明するいずれかの状態になるが、各状態のエネルギーの合計は入射したエネルギーと等価でありそれ以上にもそれ以下にもならない。これに反したレンダリング処理をすると現実感のない画像になるのである(計算で疑似的に作られたハイライトなど)。
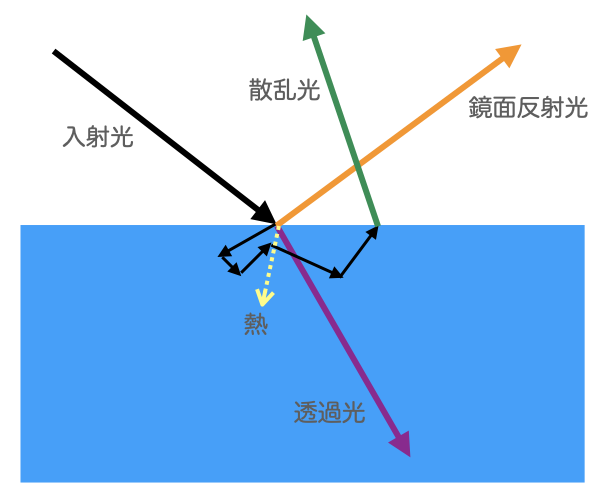
下は入射した光がその後どのような状態になるかを表した図である。
まず物体へ入射した光は、鏡面反射して物体の外へ跳ね返されるか、物体の中に吸収されるのどちらかになる。この鏡面反射する割合が鏡面反射率であり、それを $f$ とすると当然吸収される率は $1-f \quad (0 \leq f \leq 1)$になる。物体に吸収された光は、その後物体内を通り抜けていくが、ここでいくつかに分かれる。あるものは物体内をランダムな方向へ進んだのち再び外に出てくる(微小面散乱:subsurface scattering)。あるものは物体内を直進していく(透過)。そしてそれ以外は熱に換わる(発熱)。それら入射後の状態は違えど、そのエネルギーの合計は入射したエネルギーと全く同じになるのである。そこを考慮してレンダラーを設計しなければならない。
- 鏡面反射
- 物体に吸収
- 微小面散乱
- 透過
- 発熱
以後の説明では、まず物体表面が完全に滑らかな場合(平滑面)における入射光の各状態について書き、最後に滑らかでない場合(光沢面や拡散面)について補足する。
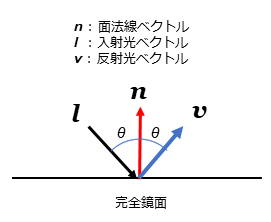
-2. 鏡面反射
光が平滑な物体に入射すると一部は面法線に対して真逆(同じ角度)の方向へ反射する。これを鏡面反射という。
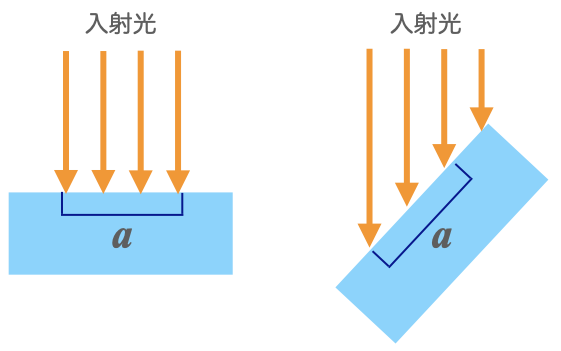
入射エネルギーの何割が反射するかを反射率と言い、これは光が入射する側の物体と衝突する側の物体の屈折率(Index of Refraction: IOR)によって決まる。光学的な正確な式は書籍1を読んでいただくとして、実装に際しては下記の式で計算できる(入射角$\theta$が0°、物体真上から垂直に物体に入射した場合)。
$$
F_0(\lambda) = \left(\frac{\eta_1(\lambda) - \eta_2(\lambda)}{\eta_1(\lambda) + \eta_2(\lambda)}\right) ^2 \qquad (1.1)
$$
ここで$\eta_1$は入射する側の物体の屈折率、$\eta_2$は入射される側の物体の屈折率である。なお屈折率とは新空中の光速を物質中の光速で割った値であり、真空の屈折率は1である。ポイントは3つある。
- 屈折率は透明じゃない物体(木や石とか)にもある
- だから金属にも屈折率はあってそれは複素数である
- 屈折率は光の波長($\lambda$)によって異なる
その物質の屈折率がわかれば反射率も「計算できる」ということになる。以前の実装では「透明でない物質の屈折率パラメータは0にし、反射率もパラメータとして別途与えていた」が、PBRの考え方では「屈折率を与えて反射率は計算で求める」ことができるわけだ。ただ金属の場合「パラメータとして与える」方が都合が良さそうだ(後述)。
反射率は入射角により大きく変化する。金属は入射角0°でも比較的高い数値だが、それ以外(誘電体とよぶ)はかなり小さい数値である。
※ このサイトが詳しい: フレネル反射率について
| 物質 | 入射角0°の反射率($F_0$) |
|---|---|
| 水 | 0.02 |
| ガラス | 0.08 |
| ダイヤモンド | 0.12 |
| 金(700nm) | 0.96 |
| 銀(700nm) | 0.97 |
一方このサイトの「フレネル反射率のグラフ」を見ると、入射角が90°に近づくにつれどんな物質も反射率が1.0に近づいていくのがわかるが、その曲線はまちまちであり特に金属では80°付近で一旦下がる場合もある。よって様々な入射角に対し反射率を正確に求めるのは負荷が高いが、そこは「Schlickの近似式」というものがあって、入射角$\theta$における反射率$F_r(\theta)$は入射角0°の反射率($F_0$)があれば程よい近似値をすぐ計算できる。実装ではこれを使う。
$$
F_r(\theta) \approx F_0 + (1 - F_0)(1 - \cos \theta)^5 \qquad (1.2)
$$
なお金属の反射率を求める方法は複素数の計算になるが、上記(1.1)式をそのまま当てはめればよい。ただし結果が複素数になるので、そのノルムを取る必要がある。たとえば金の波長700nmでの屈折率はおよそ$0.161 + 4.088i$であるから、真空から垂直に入射した時の反射率は、
\begin{align}
f &= \left(\frac{1.000 - (0.161+4.088i)}{1.000 + (0.161+4.088i)}\right)^2 \\
&= \left(\frac{0.839 - 4.088i}{1.161+4.088i}\right)^2 \\
&= \left(-0.871 - 0.453i\right)^2 \\
&= 0.553 + 0.789i
\end{align}
\begin{align}
F_0 &\approx |f| = |0.553 + 0.789i| = 0.963 \qquad (1.3)
\end{align}
となる。金属など各物質の屈折率は下記サイトも参考にさせていただいた。
-3. 散乱
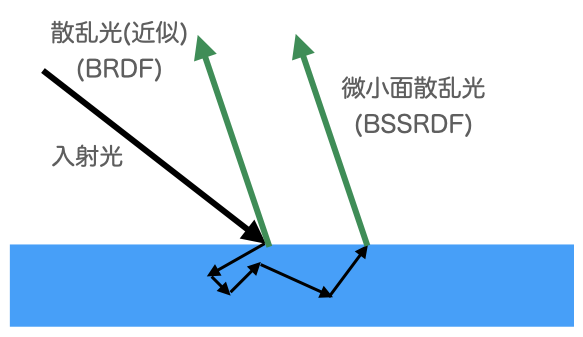
金属以外の物質(誘電体)では、鏡面反射せず物体内に光が入ることがあり、入った光の一部は内部で散乱する(分子に当たってランダムな方向に弾かれるから?)。その光が熱に換わらず最終的にもう一度物体の外に出る場合、それが物体の「色」と認識される。
内部で散乱して外に出る場合、大半は入射した場所からそれほど離れていない場所から出ると考えられるが、それを微小面散乱(subsurface scattering)という。これを真面目に計算するのがBSSRDF(双方向散乱面反射率分布関数)、入射点からそのまま反射すると仮定して近似するのがBRDF(双方向反射率分布関数)という理解。BSSRDFは負荷が高いため、レンダラーの実装ではBRDFを使うことが多いと思われる。なお書籍1にはフォトンマッピング法でこのBSSRDFを実現する手法が書いてある。
物体内を散乱する光は外へ出ずに熱へと変わる場合があるがその割合は光の波長によって異なり、それが物体色として現れてくる。赤い物質は赤以外の波長の光が内部で熱に換わりやすく、赤い光は散乱後に外へ出てきやすいということだ。なので黒い物体はほとんどの光が内部で熱に換わり、だから熱くなりやすいのだ。
PBRの話でよく出てくる「アルベド」は先の鏡面反射も含めた反射比率(入射量に対する反射量の比率)のことと思うが、私の実装では物体内に入った後で散乱もしくは透過して外に出る光の比率を「アルベド(拡散)」としてパラメータにした。
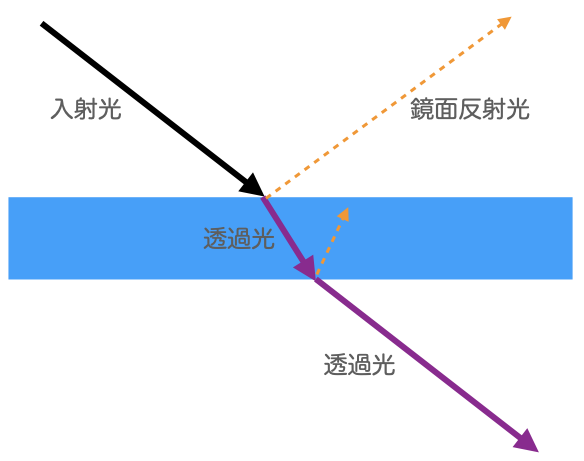
-4. 透過
物体内に入った光は上記の通り一部は散乱(か熱に変化)するが、それ以外は物体内を透過する。ガラスなどの透明な物質は光がほとんど散乱せず入射光は境界で屈折して直進し、物質の境界でさらに透過もしくは逆に反射する。
ガラスの向こうから来た光が透過して外に出てきたものを我々は目で観測するので「透明」だと感じるのだ。透過する光も波長によって透過しやすい・しにくいがあり、ステンドグラスなどの色ガラスは波長によっては途中で熱に変わってしまい外に出てこない。入射光の強度を$I_0(\lambda)$、透過して距離 $t$ 進んだあとの出射光の強度を$I(\lambda)$、単位長さあたりの光が透過する割合を$T(\lambda)$とすると、
$$
I(\lambda) = I_0(\lambda) \cdot T(\lambda)^t \qquad (1.4)
$$
と表現できる。例えば$T(\lambda)$が$0.9$とすると、$1 \mathrm{m}$進むごとに光は90%まで減衰するということだ。実装においては、この$T(\lambda)$をパラメータで与えることで色ガラスなどを表現できるようにする。
なお、光は物体内で散乱(途中で熱に変化するもの含む)・透過(途中で熱に変化するもの含む)のどちらかになるので、その確率をそれぞれ$p_d, p_t$とすると、
$$
p_d + p_t = 1 \qquad (p_d \geq 0, \quad p_t \geq 0) \qquad (1.5)
$$
である。
-5. 発熱
物質に入射した光は、鏡面反射、散乱、透過もしくは熱に変化する。金属とそれ以外で異なるので注意が必要。
- 金属: 鏡面反射かそうでなければ全て熱に変化(散乱・透過はしない)
- 誘電体: どの状態にもなりうる。
いずれにせよ、入射した光のエネルギーの一部は熱に換わるわけだが、レンダラーにとって熱は表現対象ではないので無視する。
-6. 光沢面(glossy)や拡散反射について
※ この部分は個人的な解釈なので間違いが多く含まれている可能性が特に高く、その場合は有識者の方にご指導いただきたい。
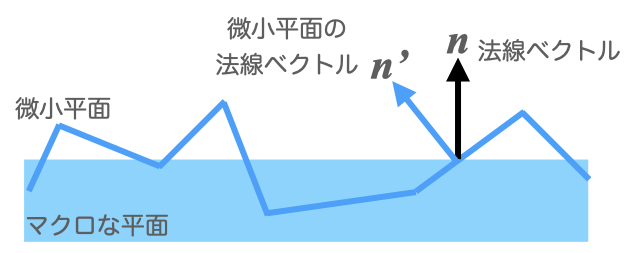
3D-CGの説明では物体表面での光の反射について、鏡面反射(磨かれた金属)か拡散反射(紙など)、もしくはその中間の反射(光沢面)のいずれかになる、といった風に書かれていることがある。間違いではないのだが、PBRを理解する上では中途半端というか、上記で書いてきたような光の物理現象と、物体表面の粗さによって生じるマクロな観測結果をごちゃ混ぜにしている気がしてならない。
物体表面がどんなに「粗い」状態であっても、非常にミクロな部分では完全に平滑な面であると考えてよく、光は入射したあと必ず上記のいずれかの状態に枝分かれしていると考えられる。
ただ粗い表面ではミクロな面の法線がマクロな物体の法線とずれているため、鏡面反射をしてもマクロでは色々な方向に光が反射するということである。だから平滑面でも粗い面でも反射する光は須く「鏡面反射」の結果である。前回記事でも書いたが、少し粗い表面にぼんやり「ハイライト」が生じるのは、この鏡面反射の結果であって、拡散反射なる別の事象ではない。
一方、ノートの紙が白っぽかったり、木が茶色系の色に見えるのは光が物体に衝突した点で「拡散反射」したのではなく、内部を少し散乱して表面に出てきた光が、散乱の結果としてランダムな方向に飛び出していくからである。それをマクロに見ると全体では方々へ拡散して反射しているように見える、というのが私の理解だ。散乱によって生じる「物体の色」と「鏡面反射」は別ものであるから、光の物理現象により生じる効果と、物体表面の粗さ度合いによって引き起こされる効果を分けて考え、実装する必要があると思う。
なお粗い物体面を正しく扱うには、本来ならマイクロファセット理論を理解する必要があろう。大雑把には、粗い表面は様々な法線方向を向いた微小な平面の集まりであり、それを考慮して反射・透過などを考えるのだが、単純に法線が色々な方向であるというだけでなく、反射したものが近くの微小平面に邪魔されて目に見えない(マスキング)状況や、近くの微小平面が覆って光が届かない(シャドウイング)状況も考慮する必要があり、厳密な計算には高度な数式の理解が必要のようだ。私もまだ勉強中なので、現時点の実装はマイクロファセット理論を反映していない。
2. 実装編
それでは次に上記理論を元に本プログラムではどのようにレンダリング処理を行なっているか、実装について述べよう。まずは物体をどのようなパラメータで定義しているかを説明し、続いてフォトン追跡、最後にレンダリング処理の実装を説明する。
なお物体内での散乱を真面目に計算するのは大変なので、実装では微小面散乱は計算せず、入射した物体表面の点で反射すると仮定した近似を使う。以後これを拡散反射と書くことにする。
-1. PBR用パラメータ
本プログラムでは、物体を表現するのにSurfaceとMaterialという2つの型を定義した。以下がその定義である。
data Surface = Surface
{ elight :: !(Maybe LightSpec) -- 発光能力
, roughness :: !Double -- 粗さ
-- calculate values
, densityPow :: !Double -- 粗さに応じたブレを計算するためのパラメータ
, alpha :: !Double -- 同上
}
data Material = Material
{ albedoDiff :: !Color -- アルベド(拡散)
, scatterness :: !Double -- 散乱度
, metalness :: !Double -- 金属性
, transmittance :: !Color -- 透過率
, ior :: !Color -- 屈折率(index of refraction, IOR)
, albedoSpec :: !Color -- アルベド(鏡面)
}
まずは簡単なSurfaceから。こちらは物体自体の発光能力を表すelightと表面の粗さを表す roughnessで構成されている。densityPowとalphaは、粗さによる微小面法線のブレの計算を高速にするため、予め計算結果を保持しておくものである。elightは別の記事で書くとして、 roughnessは0〜1の値を取り、0なら平滑面、1なら非常に粗い面となる。
次にMaterialだ。albedoDiffはアルベド(拡散)を表し、大雑把には非金属(以後、誘電体)の物体色である(若干意味合いが違うがBSDFのところで説明)。scatternessは誘電体に入ってきた光が散乱するのか真っ直ぐ通り抜けるのかの比率を表し、不透明な物体やガラスのような透明な物体を表現するのに使う。metalnessは文字通り金属性で、0なら誘電体、1なら金属を意味する。0.5などの中間値は、本プログラムでは扱わない。自然界には金属か誘電体かのどちらかしかないためである(一部人工物はそのような処理をしたものがあるようだが対象外とする)。transmittanceは透過率で、式(1.4)の $T(\lambda)$ である。iorは屈折率である。プリズムのように光の波長ごとに異なる場合があるためRGB3色で指定する。最後のadbedoSpecはアルベド(鏡面)という意味合いの名付けだが、実際には式(1.1)で求められる$F_0$が入る。プログラム中では、指定しなければ屈折率から(1.1)を用いて計算し、指定すればそのままの値がセットされる。金属も複素数の屈折率にすれば計算できるが、金属の微妙な色合い(赤みのある金とか、IORの情報がない金属など)を表現したい場合もあるので指定できるようにしている。
-2. フォトン追跡
次にフォトン追跡だ。この処理は理論編で書いた光の挙動をそのままプログラムに落とし込む感じだ。関数の構造としては次のようにtracePhotonがメインで、その中でnextDirectionさらにphotonBehaviorが呼ばれる。理論編との関連がわかりやすいように後ろから説明する。
tracePhoton → nextDirection → photonBehavior
■ photonBehavior関数
物体表面での光の挙動を決定するのはphotonBehaviorである。
photonBehavior :: Material -> Double -> Wavelength -> IO PhotonBehavior
photonBehavior (Material aldiff scat _ _ _ alspec) cos wl = do
let
f = fresnelReflectance (selectWavelength wl alspec) cos
r1 <- russianRouletteBinary f
if r1 == True
then return SpecularReflection
else do
r2 <- russianRouletteBinary (selectWavelength wl aldiff)
if r2 == False
then return Absorption
else do
r3 <- russianRouletteBinary scat
if r3 == False
then return SpecularTransmission
else return DiffuseReflection
この関数は、物体に入射した光が以下の4種類のいずれになるかを確率で求める。
- 鏡面反射:
SpecularReflection - 吸収:
Absorption - 鏡面透過:
SpecularTransmission - 拡散反射:
DiffuseReflection
最初に入射角(cos)に応じて鏡面反射率 $F_r$ を求める(f)。次に確率を使って挙動を決めるためrussianRouletteBinaryという関数を使っている。これは 0〜1 の間の実数を引数に取り、乱数を生成して引数以下ならTrue、より大きければFalseを返す。なのでr1は鏡面反射率以下なら「鏡面反射」し、そうでなければ以下に続く、という具合だ。
次にアルベド(拡散)以下かどうかを確率で決め、より大きい(False)なら光は「吸収」されるとする。最後は散乱度を使った判定で、それより大きければ「鏡面透過」、以下なら「拡散反射」とする。
■ nextDirection関数
次はnextDirectionだ。これはphotonBehaviorの結果を元に、光が次に進む方向を計算している。結果はMaybe型、進む方向が無ければNothingを返す。戻り値は方向ベクトルと真偽値のペアだが、真偽値は物体で反射したらTrue、中に入ったらFalseとなる。
nextDirection :: Material -> Surface -> Double -> Direction3 -> Photon -> IO (Maybe (Direction3, Bool))
nextDirection mate surf eta nvec (wl, (_, vvec)) = do
nvec' <- microfacetNormal nvec vvec surf (metalness mate) --(1)
case nvec' of
Nothing -> return Nothing
Just nvec' -> do
let (rdir, cos1) = specularReflection nvec' vvec --(2)
if rdir <.> nvec < 0.0
then return Nothing
else do
pb <- photonBehavior mate cos1 wl --(3)
case pb of
SpecularReflection -> return $ Just (rdir, True) -- 鏡面反射
Absorption -> return Nothing -- 吸収
DiffuseReflection -> do
df <- diffuseReflection nvec
return $ Just (df, True) -- 拡散反射
SpecularTransmission -> do -- 鏡面透過
let (tdir, _) = specularRefraction nvec' vvec eta cos1
case tdir of
Just tdir -> do
if tdir <.> nvec > 0.0
then return Nothing
else return $ Just (tdir, False)
Nothing -> return Nothing
(1) 微小平面の法線ベクトル
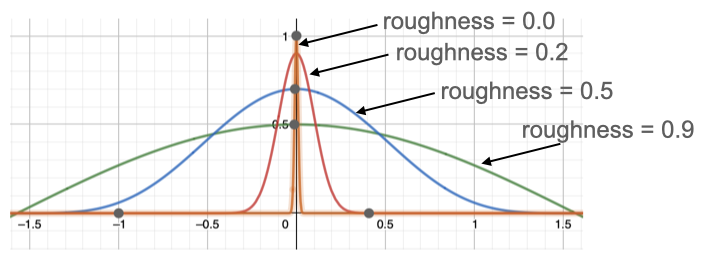
一番最初のmicrofacetNormalは、微小平面での法線ベクトルを面の粗さをもとに計算しており、粗いほどマクロな法線ベクトルからズレる(下図)。横軸はラジアン、縦軸は確率で、roughnessが小さいほどマクロな法線ベクトルとの差がなく、大きいほど周りに広がるようにズレる可能性が高まる。
以後の追跡はこの微小平面での法線ベクトル(nvec')を元に行う。nvec'がNothingになるとはどういうことか?例えば下図のように微小平面でフォトンの入射($l$)が面の裏側から入る場合を想定している。ただおそらく正しくこの辺を処理するためにはマイクロファセット理論をちゃんと理解しつつ金属か誘電体かなども考慮した実装が必要であろう。現時点ではそこは保留し、「フォトンの入射 $l$(vvec)と微小面法線 $n'$(nvec')とのなす角が90°以上ならNothing」と簡略化している。

図7:微小平面の法線ベクトル (n'と-lのなす角が90°を超えている)
(2) 反射ベクトル
nvec'が求まった場合、次に微小平面での反射ベクトル(rdir)、およびnvec'とrdirのなす角 $\theta$ としたときの $\cos \theta$ を求めている。その直後に反射ベクトルとマクロな面法線ベクトル(nvec)の角度を確認し、もし反射ベクトルが面の裏側方向を向いていたら追跡を打ち切る。
(3) フォトンの次の状態を決定
最後にphotonBehaviorによりフォトンの次の状態を決定し、状態に応じたフォトンの向かう方向を決めてやる。方向と一緒に境界面での反射か屈折かを表すBool値を返している。
■ tracePhoton関数
最後にtracePhotonを示そう。
tracePhoton :: V.Vector Object -> Int -> Material -> Material
-> (Photon, RadEstimation) -> IO (V.Vector Photon)
tracePhoton !objs !l !mate_air !mate0 (!photon@(wl, ray@(_, vvec)), !radest)
| l >= max_trace = return V.empty
| otherwise = do
case (calcIntersection ray objs) of
Just is -> do
let
(t, (pos, nvec), (mate, surf), io) = is
tracer = tracePhoton objs (l+1) mate_air
ref <- do
-- フォトンが物体に到達するまでに透過率が低く吸収される場合あり
-- transmission ** t の確率で到達する
let
tr = (selectWavelength wl (transmittance mate0)) ** t --(1)
i <- russianRouletteBinary tr
if i == False
then return V.empty
else do
let
mate' = if io == In then mate else mate_air
eta = relativeIorWavelength (ior mate0) (ior mate') wl
nextdir <- nextDirection mate surf eta nvec photon
case nextdir of
Just (dir, mf) -> do
let mate'' = if mf == True then mate0 else mate'
tracer mate'' ((wl, initRay pos dir), PhotonMap)
Nothing -> return V.empty
if (radest == PhotonMap || l > 0) && storePhoton mate == True --(2)
then return $ V.cons (wl, (pos, vvec)) ref
else return ref
Nothing -> return V.empty
(1) 透過中の光の吸収
まずは反射・屈折回数が制限値(現状は10回)を超えたら追跡を終了させている。そうでない場合はまずレイと物体の交点を求める。交点がある場合、まず以下の部分でフォトンが物体に到達したかどうかを判定する。今フォトンが進んでいる物体の透過率を元に、交点までの距離を踏まえ交点に到達するかどうかを判断しているわけだ。
let
tr = (selectWavelength wl (transmittance mate0)) ** t
i <- russianRouletteBinary tr
if i == False
:
Falseなら到達しないので、やはり追跡は終了する。理論編では「フォトンが物体にぶつかった後」で透過後吸収されると書いたが、実装でそうしようとすると、さらに次の交点を求めてからでないと判断できず、さらに次の交点、、、と終わりがない。よって最初に判定しておく。
その後はnextDirectionの結果に従いフォトン追跡を繰り返すだけ。
(2) フォトンマップへの記録
ただし「拡散反射」の場合だけは、あとでフォトンマップにするため交点情報を記録しておく。この条件はわかりにくいので補足する。
if (radest == PhotonMap || l > 0) && storePhoton mate == True
前半はフォトンマッピングの作成とレンダリングの高速化・品質向上のための仕組みなので、機会があれば記事にしようと思う。後半の条件storePhoton mate == Trueは、「拡散反射の場合」だ。
以上がフォトン追跡の実装だ。
-3. レンダリング
レンダリングも理論編に沿ってプログラムに落とし込んである。関数の構造は、メインがtraceRayでその最後にbsdfを呼んで物体上の交点での輝度を決定する流れだ。
traceRay → bsdf
■ BSDF
traceRayの処理がわかりやすくなるように、まずはbsdf関数から始めよう。この関数はいわゆるBSDF(双方向散乱分布関数)の実装である。BSDFはBRDF(双方向反射率分布関数)とBTDF(双方向透過率分布関数)を組み合わせる形になっている。それらの関数の数式をおさらいしよう。詳細は最初に挙げたURL4に詳しく記載されており、それを参考に組んである。
とある物体の表面上の点からある方向(視点方向, $\omega_o$)へ出射される光の放射輝度 $L_o(\omega_o)$ は、面自体が発光して放射される放射輝度 $L_e$ と各方向から来る光がその点で反射屈折される放射輝度 $L_i$ の和である。
$$
L_o(\omega_o) = L_e + L_i \qquad (2.1)
$$
$L_i$は双方向反射率散乱分布関数(BRDF) $f_r$ と双方向透過率分布関数(BTDF) $f_t$ を用い、面の上半分の半球方向から来る反射光、下半分の半球方向から来る屈折光を集計するので積分を使って以下のように表せる。
\begin{align}
L_i(\omega_i) &= \int_{\Omega} f_r dE_r(\omega_i) + \int_{\Omega} f_t dE_t(\omega_i) \\
&= \int_{\Omega} f_r dL_r(\omega_i) |n \cdot \omega_i| + \int_{\Omega} f_t dL_t(\omega_i) |n \cdot \omega_i| \qquad (2.2)
\end{align}
と表せる。ここで、$\omega_i$は特定方向を表す方向ベクトル、$n$は面の法線ベクトルとし、放射輝度 $dL(\omega_i)$ と放射照度 $dE(\omega_i)$ の関係は $dL(\omega_i) |n \cdot \omega_i| = dE(\omega_i)$ である。一旦積分から離れて入射方向$\omega_i$から来る光について書くと、
$$
dL_i(\omega_i) = f_r dL_r(\omega_i) |n \cdot \omega_i| + f_t dL_t(\omega_i) |n \cdot \omega_i| \qquad (2.3)
$$
となる。この$f_r$と$f_t$を決めるのだが、$f_r$ は鏡面反射と拡散反射に分けて考えよう。それぞれ $f_{r,s}$ と $f_{r,d}$ とする。URL4を参考に最もシンプルなものを採用する。なお関数 $f$ は、入射方向と出射方向に依存するため $f(\omega_o, \omega_i)$と書くべきだが端折ることにする。
\begin{align}
f_{r,s} &= \frac{F_r(\omega_i)}{|n \cdot \omega_i|} \\
f_{r,d} &= \frac{\rho}{\pi} \\
f_t &= \left(\frac{\eta_2}{\eta_1}\right)^2 \frac{(1 - F_r(\omega_i))}{|n \cdot \omega_i|}
\end{align}
ここで、$F_r$は式(1.2)で求めた反射率、$\rho$はアルベド(拡散)である。これらを単純に式(2.3)に代入すると($|n \cdot \omega_i|$ は相殺されて)
\begin{align}
dL_i(\omega_i)
&= \frac{F_r(\omega_i)}{|n \cdot \omega_i|} dL_{r,s}(\omega_i) |n \cdot \omega_i| + \frac{\rho}{\pi} dL_{r,d}(\omega_i) |n \cdot \omega_i| + \left(\frac{\eta_2}{\eta_1}\right)^2 \frac{(1 - F_r(\omega_i))}{|n \cdot \omega_i|} dL_t(\omega_i) |n \cdot \omega_i| \\
&= F_r(\omega_i) dL_{r,s}(\omega_i) + \frac{\rho}{\pi} dL_{r,d}(\omega_i) |n \cdot \omega_i| + \left(\frac{\eta_2}{\eta_1}\right)^2 (1 - F_r(\omega_i)) dL_t(\omega_i) \qquad (2.4)
\end{align}
となる。しかしこれでは拡散反射光成分と透過光成分が過剰に集計されてしまう(と思う)ので、さらに手を加える。PBR用パラメータに「散乱度」入れたのはこのためだ。散乱度は物体内に吸収された光がランダムな方向へ散乱するか直進するかの比率だった。これを$s$として、拡散反射光と透過光を組み合わせる。さらに、アルベド $\rho$ についても拡散反射にのみ適用されるのではなく「物体に吸収された光全体」に適用されると解釈し、次の式(2.5)を本プログラムのレンダリングの式とする。なお入射する拡散反射光は実装時の処理を考慮し、放射照度$E_d$に戻した。
\begin{align}
dL_i(\omega_i) &= F_r(\omega_i) dL_{r,s}(\omega_i) + \left( 1 - F_r(\omega_i) \right) \rho \left( s \cdot \frac{1}{\pi} dL_{r,d}(\omega_i) |n \cdot \omega_i| + (1 - s) \left(\frac{\eta_2}{\eta_1}\right)^2 dL_t(\omega_i) \right) \\
&= F_r(\omega_i) dL_{r,s}(\omega_i) + \left( 1 - F_r(\omega_i) \right) \rho \left( s \cdot \frac{1}{\pi} dE_d(\omega_i) + (1 - s) \left(\frac{\eta_2}{\eta_1}\right)^2 dL_t(\omega_i) \right) \qquad (2.5)
\end{align}
さて、本来求めたいのは全球方向から入射する光が集計された$L_i$である。
$$
L_i = \int_{\Omega} dL_i(\omega_i)
$$
拡散反射面やざらついた面での鏡面反射(ハイライト含む)・屈折を表現するにはこの積分が必要だ。これについては素のフォトンマッピング法ではなく「プログレッシブ」フォトンマッピング法で対処する(第13回参照)。この手法では、一つのシーンの描画を光線の方向をランダムにズラしながら100回、1000回と何度も繰り返して輝度を求める。この繰り返しにより、様々な方向$\omega_i$からの光を合計することにより上記積分の近似値を求めるのだ。
※ 拡散反射光については本当はちょっと違う。各$\omega_i$方向からの光を繰り返しにより全方向分集計するというより、一回でいくつかの方向から採取した光を集計するが、繰り返しにより採取する光の数を増やして精度を向上させる感じだ。
上記を踏まえBSDFは次のようになった。
bsdf :: Material -> Surface -> Double -> Double -> Double -> Radiance -> Radiance -> Radiance -> Radiance
bsdf (Material aldiff scat metal _ _ alspec) (Surface _ rough _ _) cos1 cos2 eta ed ls lt =
if metal == 1.0
then fr <**> ls
else (1.0 - rough) *> fr <**> ls +
((1.0 - metal) *> (aldiff * nfr)) <**>
((scat * one_pi) *> ed + ((1.0 - scat) * eta * eta) *> lt)
where
fr = fresnelReflectanceColor alspec cos1 -- Fr
nfr = negate fr -- (1 - Fr)
なおif metal == 1.0は「金属だったら」であり、金属面は拡散反射光、屈折光はないので鏡面反射成分のみである。また、
else (1.0 - rough) *> fr <**> ls +
の(1.0 - rough)は、誘電体の場合の補正で、面が粗くなるほど鏡面反射成分を少なくするものだ。これがないと完全な拡散面なのに鏡面反射成分が所々強くなる(たまたま反射方向に光源があったとか)ことがあり、ノイズのようになる。この処置が適切かどうかは不明であるが。
■ レンダリング本体
最後にtraceRay関数を示そう。ちょっと長い。
traceRay :: PhotonFilter -> V.Vector Object -> V.Vector LightObject -> Int
-> V.Vector PhotonMap -> Double -> Material -> Material -> Ray
-> IO Radiance
traceRay !filter !objs !lgts !l !pmaps !radius !mate_air !mate0 !ray@(_, vvec)
| l >= max_trace = return radiance0
| otherwise = do
case (calcIntersection ray objs) of
Nothing -> return radiance0
Just is@(t, sfpt@(pos, nvec), (mate, surf), io) -> do
let metal = metalness mate
-- E_diffuse
ed <- if metal /= 1.0 && scatter mate
then do
lrads <- V.mapM (getRadianceFromLight2 objs sfpt) lgts
let
ed_f = lrads `deepseq` foldl (+) radiance0 $ V.catMaybes lrads -- 計算による放射照度
ed_p = estimateRadiance radius filter pmaps is -- 放射輝度推定による放射照度
return (ed_f + ed_p)
else return radiance0
-- preparation for L_spec and L_trans
let
tracer = traceRay filter objs lgts (l+1) pmaps radius mate_air
nvec' <- microfacetNormal nvec vvec surf (metalness mate)
let
(rvec, cos1) = case nvec' of
Nothing -> specularReflection nvec vvec
Just nvec' -> specularReflection nvec' vvec
-- L_spec
ls <- if nvec' /= Nothing && rvec <.> nvec > 0.0 &&
(metal == 1.0 || (metal /= 1.0 && roughness surf /= 1.0))
then tracer mate0 (pos, rvec)
else return radiance0
-- L_trans
(lt, eta, cos2) <- if nvec' /= Nothing && refract mate
then do
let
mate' = if io == In then mate else mate_air
eta' = relativeIorAverage (ior mate0) (ior mate')
(tvec, cos2') = specularRefraction (fromJust nvec') vvec eta' cos1
case tvec of
Nothing -> return (radiance0, eta', cos2')
Just tvec -> do
if tvec <.> nvec <= 0.0
then do
lt' <- tracer mate' (pos, tvec)
return (lt', eta', cos2')
else return (radiance0, 1.0, 0.0)
else return (radiance0, 1.0, 0.0)
let
tc = expColor (transmittance mate0) t
li = bsdf mate surf cos1 cos2 eta ed ls lt
le = emittance surf sfpt vvec
return (tc <**> (le + li))
この関数は視線(や反射・屈折したレイ)と物体の交点を求めたのち、その点に外から入ってくる光の量を求めた後BSDFにてまとめる、ということをやっている。
拡散反射光
最初に拡散反射光 $dE_d$ (ed)を求める。条件は以下の通り。
- 金属でない
- 物体内に吸収された光が少しでも散乱する(
scatternessが0でない)
拡散反射光は原則としてフォトンマップから放射輝度推定にて計算するが、高速化と品質向上のため直接光(光源から直接物体面に届く光)は計算にて求める方法も用意している。ed_fが直接光を計算式で求めている部分、下のed_pがフォトンマップから放射輝度推定している部分である。
lrads <- V.mapM (getRadianceFromLight2 objs sfpt) lgts
let
ed_f = lrads `deepseq` foldl (+) radiance0 $ V.catMaybes lrads -- 計算による放射照度
ed_p = estimateRadiance radius filter pmaps is -- 放射輝度推定による放射照度
なお、BSDFの説明の時に拡散反射光だけ放射照度($dE_d$)としたのは、計算にしろフォトンマップを使うにしろ得られるのが放射輝度ではなく放射照度だからである。計算で求める時は getRadianceFromLight2 経由でcalcRadiance関数を呼ぶが、そこに入射角の余弦(cos)を掛けている部分がある。これにより照度が得られる。
calcRadiance :: LightSpec -> V.Vector Object -> SurfacePoint -> SurfacePoint -> Double -> Maybe Radiance
calcRadiance lgtspec objs (pos, nvec) (lpos, lnvec) area
:
| otherwise = Just ((area * cos / dist2) *> rad)
where
:
cos = nvec <.> lvec
:
一方放射輝度推定ではフォトンマップから微小平面内のフォトンを集めて合計するのだが、この操作がそもそも照度を求めているのである。というか(大雑把に言って)フォトンの密度が照度である。
反射屈折の前準備
反射光、屈折光を求める前に、マイクロファセット理論を参考に物体面の粗さを踏まえた微小平面の法線ベクトル(nvec')を求める。これを元にして反射方向ベクトル(rvec)を計算しているのだ。nvec'が求まらない場合(遮蔽されているなどを想定)はダミーでマクロな法線ベクトルを代わりに使って計算している(が、使わない)。
nvec' <- microfacetNormal nvec vvec surf (metalness mate)
let
(rvec, cos1) = case nvec' of
Nothing -> specularReflection nvec vvec
Just nvec' -> specularReflection nvec' vvec
鏡面反射光
こちらはかなり単純だ。以下の条件を満たす場合、交点から反射方向へ向かってレイトレースする。
- 微小面法線ベクトル
nvec'が存在する - 微小面での反射ベクトルがマクロな面の表側である(内部に入り込まない)
- 金属 or 誘電体の場合は粗さが最大(1.0)ではない
透過光
透過光を求める条件は次の通り。
- 誘電体である(金属は光を透過しない)
- 物体内に吸収された光が完全に散乱してしまわない(
scatternessが1.0ではない)
次にspecularRefraction関数で屈折ベクトルを求める。存在しない(全反射など)の場合はもしくは、面が粗い場合に屈折ベクトルが物体の表側に出てしまう場合は追跡をやめる。
輝度値の計算
最後に上記で求めた光を統合する。
let
tc = expColor (transmittance mate0) t
li = bsdf mate surf cos1 cos2 eta ed ls lt
le = emittance surf sfpt vvec
return (tc <**> (le + li))
拡散反射光($E_d$)、鏡面反射光($L_s$)、透過光($L_t$)をBSDFで統合し $L_i$ とする。また物体表面自体の発光はSurfaceのemittanceに出射方向(角度)を考慮して $L_e$を求める。これらを足し合わせ、視点から交点までの間の減衰量(tc)を考慮して最終的な輝度を返す。
■ マイクロファセットの考慮
所々で言及したように、本プログラムの実装では多少マイクロファセットを意識している。レンダリングに使う式(2.5)は非常に基本的なものであり、現在主流のマイクロファセット理論に基づいた下のような式ではない。
$$
f_r = \frac{D(\omega_i, \omega_o) G(\omega_i, \omega_o) F_r(\omega_i, \omega_o)}{4 |n \cdot \omega_i| |n \cdot \omega_o|}
$$
ここで、$D$は面の粗さに応じてズレる微小面法線ベクトルの分布、$G$は同じく粗さに応じた光の遮蔽の分布である。
このうち$D$については、独自に粗さに応じた法線ベクトルのズレを実装しているので同じような効果は出せていると思われる。一方$G$については、マクロな法線ベクトルと$D$に基づき求めた反射屈折ベクトルが理論上おかしい(反射ベクトルが面の裏側に回るなど)場合を除いて何ら考慮されていない。この辺は今後の検討課題である。
3. 作例とまとめ
上記に基づいて実装したレンダラーによる作例をいくつか示す。
| 各ボールの材質 | 画像 |
|---|---|
| ざらついた銅、透明ガラス、ツルツルのプラスチック |  |
| 磨かれた銅、半透明なプラスチック、マットなプラスチック |  |
| 石膏、色ガラス、ツルツルのプラスチック |  |
概ねそれっぽい材質が表現できているのではないかと思う。ただ石膏のボールはちょっと滑らかすぎる感じがする。これについてはOren-Nayerモデルの検討も必要かもしれない。
今回は物理ベースレンダリング(PBR)について、自分の理解しているところを忘備録として記事にしてみた。書いている途中で理解があやふやなところ、間違っていたところは都度各種情報を読みながら修正し、それにともなってプログラムにも多くの修正を入れることができた。少し長い記事になったが、自分としては有益であった。一方でPBRは、反射モデルも多種多様なものが発表・使用されており高度な理論に基づいた複雑で高度なレンダリングが存在する。まだまだ学び改善することは多い。
(参考)
現在の実装はこちら