離散フーリエ変換から離散コサイン変換までの式展開

はじめに

離散フーリエ変換 (fft) を使って離散コサイン変換を計算する式を確認してみました。せっかくなので備忘録代わりに Qiita に残しておきます。MATLAB 関数もつけてます。

ただ式展開はできたものの、それがどういう意味を持つのかいまいちピンと来ていません。離散フーリエ変換に詳しい方コメントお待ちしております。。

背景

以前、離散コサイン変換を使ってポワソン方程式を数値的に解きました。

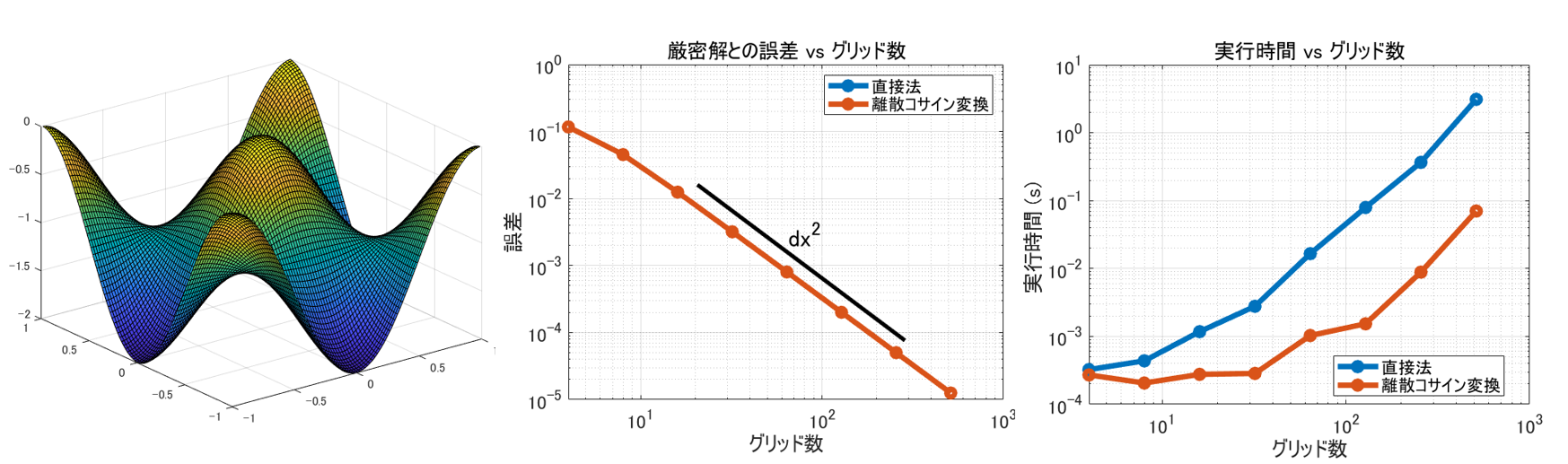
参照：Qiita: 離散コサイン変換でポアソン方程式を高速に解く

離散コサイン変換自体は MATLAB 本体の fft 関数を使っても実現可能（例えばこれ File Exchange: dctt）ですが、あるものは使った方が楽なので今回は dct または dct2 を使います。

と書いた通り、この時は離散コサイン変換を計算する関数 dct (Signal Processing Toolbox) を使いましたが、理解を深めるため離散フーリエ変換 (fft) を使って離散コサイン変換を計算してみます。File Exchange: dctt のように、同じことをする MATLAB 関数は公開されていますが、中身の理解に繋がれば嬉しいです。

ご存知の通り fft は MATLAB 本体の関数ですので、まぁいろいろと都合がいいですよね。

成果物

• mydct2.m： dct のデフォルト設定である離散コサイン変換（DCT-Ⅱ）
• mydct3.m： idct のデフォルト設定である離散コサイン変換（DCT-Ⅲ）

MATLAB コード：mydct2.m

function b = mydct2(a)

arguments
   a (:,1)  
end

N = size(a,1);
% a(1), a(2), ..., a(N), a(N), a(N-1), ..., a(1);
xx = [a;flipud(a)]; % DCT2
tmp = fft(xx);
xd = tmp(1:N);
ww = 1/sqrt(2*N)*exp(-1i*pi*(0:N-1)/(2*N)).';
b = xd.*ww;
b(1) = b(1)/sqrt(2);
b = real(b);

MATLAB コード：mydct3.m

function b = mydct3(a)

arguments
   a (:,1)  
end

N = length(a);
% a(1), a(2), ..., a(N), 0, a(N), a(N-1), ..., a(2);
xx = [a;0;flipud(a(2:N))]; % DCT3
xx(1) = xx(1)*sqrt(2);

% weight
ww = exp(-1i*pi*(0:2*N-1)/(2*N)).';
ww(N+2:end) = ww(N+2:end)*exp(-1i*pi);
xxw = xx.*ww;
tmp = fft(xxw)/sqrt(2*N);
b = real(tmp(1:N));

以下、試しに実行してみた結果ですが、お互いに逆変換になっていることが確認できます。

> x = rand(5,1);
> [dct(x), mydct2(x)]
    1.2665    1.2665
    0.0617    0.0617
   -0.3532   -0.3532
    0.1282    0.1282
   -0.1272   -0.1272
> [idct(x), mydct3(x)]
    1.2855    1.2855
   -0.2943   -0.2943
   -0.0748   -0.0748
    0.1331    0.1331
   -0.0531   -0.0531

Which DCT are you talking about?

MATLAB の dct 関数ではいろんな状況に合わせて¹ DCT-Ⅰ から DCT-Ⅳ まで 4 つの DCT が実装されています²が、ここでは前回ポワソン方程式を解く際にも使っている代表的な離散コサイン変換 DCT-Ⅱ と DCT-Ⅲ を見てみます。上で確認したように、それぞれが互いに逆変換になってます。

fft から dct へ

DCTは、ある有限長シーケンスを交互反転させながら周期信号へと拡張し、その信号に対して離散フーリエ変換（Discrete Fourier Transform; DFT）を適用することと等価です。交互反転させることで一周期分が偶対称となり、結果的にコサイン成分だけが残ることからDCTが導かれます。(妻夫木で学ぶDCT から³)

いずれにしても、もともとのデータを周期信号へと拡張し fft をかけるというのは共通しています。要は拡張の仕方。FFTW のレファレンスにも解説ページがあります。

参考：Real even/odd DFTs (cosine/sine transforms)

定義式

ここで定義式は MATLAB 公式 doc ページのものを使います。

離散コサイン変換: dct
高速フーリエ変換: fft

長さ $N$ の信号 $x$ に対して離散フーリエ変換を $Y(k)$、離散コサイン変換を $y(k)$ とおきます。$\delta_{k1}$ はクロネッカーデルタです。

\begin{align}
{\rm DCT-I\hspace{-.1em}I} : y(k) &= \sqrt{\frac{2}{N}} \sum_{j=1}^{N} x(j) \frac{1}{\sqrt{1+\delta_{k1}}} \cos{\left( \frac{\pi}{2N} (2j-1) (k-1) \right)}, \\
{\rm DCT-I\hspace{-.1em}I\hspace{-.1em}I} : y(k) &= \sqrt{\frac{2}{N}} \sum_{j=1}^{N} x(j) \frac{1}{\sqrt{1+\delta_{j1}}} \cos{\left( \frac{\pi}{2N} (j-1) (2k-1) \right)}, \\
{\rm FFT} : Y(k) &= \sum_{j=1}^{N} x(j) \exp{\left( \frac{-2 \pi i}{N} (j-1)(k-1) \right)}.
\end{align}

注: ご存知の通り MATLABのベクトルは $0$ から $N – 1$ ではなく $1$ から $N$ で定義されるため、 和は $1$ から $N$ としています。コピペするときは要注意（笑）

DCT-Ⅱ

代表的な離散コサイン変換です。

ここでは $x(1)$ ~ $x(N)$ を以下のように拡張します。

x(1),x(2), x(3), \cdots, x(N), x(N), x(N-1), \cdots, x(2), x(1)

全長 $2N$ です。$j=0.5$ もしくは $j=N+0.5$ を中心に対称性がある感じですね。

周期信号へと拡張した長さ $2N$ の離散フーリエ変換を考えて

w(k) = \exp{\left( \frac{-\pi i}{2N} (k-1) \right)},

という重みをかけた式を展開していきます。半サンプル分データをシフトすることに対応する処理と理解しています。そうすることで $\sin$ 項が消えて $\cos$ 項のみが残るはず。

上の定義式から

\begin{align}
Y(k) w(k) &= \sum_{j=1}^{2N} x(j) \exp{\left( \frac{-\pi i}{2N} (2j-1)(k-1) \right)}, \\
&= \sum_{j=1}^{N} x(j) \exp{\left( \frac{- \pi i}{2N} (2j-1)(k-1) \right)} 
+ \sum_{j=N+1}^{2N} x(j) \exp{\left( \frac{- \pi i}{2N} (2j-1)(k-1) \right)}. 
\end{align}

ここで冒頭の図で示した拡張した通り $x(j) = x(2N-j+1)$ の関係を使うと、右辺は

\begin{align}
\sum_{j=N+1}^{2N} x(j) \exp{\left( \frac{- \pi i}{2N} (2j-1)(k-1) \right)} 
&= \sum_{j=1}^{N} x(j) \exp{\left( \frac{- \pi i}{2N} (4N-2j+2-1)(k-1) \right)}, \\
&= \sum_{j=1}^{N} x(j) \exp{\left( \frac{ \pi i}{2N} (2j-1)(k-1) -2\pi i(k-1) \right)}, \\
&= \sum_{j=1}^{N} x(j) \exp{\left( \frac{ \pi i}{2N} (2j-1)(k-1) \right)}.
\end{align}

と展開されます。そして結局予定通り $\sin$ 項が消えて

\begin{align}
Y(k) w(k) &= \sum_{j=1}^{N} x(j) \exp{\left( \frac{- \pi i}{2N} (2j-1)(k-1) \right)} + \sum_{j=1}^{N} x(j) \exp{\left( \frac{ \pi i}{2N} (2j-1)(k-1) \right)}, \\
&= 2 \sum_{j=1}^{N} x(j) \cos{\left( \frac{\pi}{2N} (2j-1) (k-1) \right)}, \\
&= y(k) \sqrt{2N} \sqrt{1+\delta_{k1}},
\end{align}

となり、最終的に以下の通り DCT-Ⅱ と DFT の関係が求まりました。

y(k) = \frac{Y(k) w(k)}{\sqrt{2N} \sqrt{1+\delta_{k1}}}. 

これを実装した mydct2.m はこちらで紹介した通りです。

DCT-Ⅲ

次は DCT-Ⅲ です。こちらは DCT-Ⅱ の逆変換となっており、idct のデフォルトの挙動でもあります。この場合は、 $x(1)$ ~ $x(N)$ を以下のように拡張すると考えます。

x(1),x(2), x(3), \cdots, x(N), 0, x(N), x(N-1), \cdots, x(2)

$x(N+1) = 0$ であり、$x(1)$ は繰り返されていない点に注意。全長 $2N$ です。$j=1$ を中心に対称性がある感じですね。

今度は $x'(j)$ に重みをかけた $x'(j) w(j)$ の DFT から始めます。$x(1)$ の値をいじるので $x'(j)$ と変えておきます。また $w(j)$ は以下のように定義します;

w(j) = \left\{ \begin{array}{ll}
\exp{\left( \frac{-\pi i}{2N}(j-1) \right)} & (1 \lt j \lt N), \\
\exp{\left( \frac{-\pi i}{2N}(j-1) -\pi i \right)} = \exp{\left( \frac{-\pi i}{2N}(j-1+2N) \right)} & (N+1 \lt j \lt 2N). \\
\end{array} \right.

・・・無理やり感がありますが、進めます。

重みを付けているので $Y'(k)$ とおきます。

\begin{align}
Y'(k) &= \sum_{j=1}^{2N} x'(j)w(j) \exp{\left( \frac{-2 \pi i}{2N} (j-1)(k-1) \right)}, \\
&= x'(1) + \sum_{j=2}^{N} x'(j) \exp{\left( \frac{- \pi i}{2N} (j-1)(2k-1) \right)} \\
&+ \sum_{j=N+2}^{2N} x'(j) \exp{\left( \frac{- \pi i}{2N} (j-1)(2k-1) -\pi i \right)}. 
\end{align}

ここで拡張方法に由来する $x'(N+1) = 0$ 及び $x'(j) = x(2N-j+2)$ for $j>1$ を使うと、右辺は

\begin{align}
\sum_{j=N+2}^{2N} x'(j) \exp{\left( \frac{- \pi i}{2N} (j-1)(2k-1) -\pi i \right)} 
&= \sum_{j=2}^{N} x'(j) \exp{\left( \frac{- \pi i}{2N} (2N-j+2-1)(2k-1) -\pi i \right)}, \\
&= \sum_{j=2}^{N} x'(j) \exp{\left( \frac{\pi i}{2N} (j-1)(2k-1) -2k\pi i \right)}, \\
&= \sum_{j=2}^{N} x'(j) \exp{\left( \frac{\pi i}{2N} (j-1)(2k-1) \right)}, 
\end{align}

ということで、

\begin{align}
Y'(k) &= x'(1) + \sum_{j=2}^{N} x'(j) \exp{\left( \frac{- \pi i}{2N} (j-1)(2k-1) \right)}
+ \sum_{j=2}^{N} x'(j) \exp{\left( \frac{\pi i}{2N} (j-1)(2k-1) \right)}, \\
&= x'(1) + 2 \sum_{j=2}^{N} x'(j) \cos{\left( \frac{\pi}{2N} (j-1) (2k-1) \right)}, \\
&= 2 \sum_{j=1}^{N} \frac{1}{\sqrt{1+\delta_{j1}}} x(j) \cos{\left( \frac{\pi}{2N} (j-1) (2k-1) \right)}, \\
&= \sqrt{\frac{2}{N}} \sum_{j=1}^{N} x(j) \frac{1}{\sqrt{1+\delta_{j1}}} \cos{\left( \frac{\pi}{2N} (j-1) (2k-1) \right)} \sqrt{2N},  \\
&= y(k) \sqrt{2N}. 
\end{align}

$y(k)$ は $x(j)$ に対する DCT-Ⅲ であり、ここで $j \le 2$ では $x(j) = x'(j)$ そして $\sqrt{2}x(1) = x'(1)$.

最終的に以下の通り DCT-Ⅲ と DFT の関係が求まりました。

y(k) = \frac{Y'(k)}{\sqrt{2N}}. 

これを実装した mydct3.m はこちらで紹介した通りです。

まとめ

離散コサイン変換 DCT-Ⅱ と DCT-Ⅲ が計算できるようにはなりました。

DCT-Ⅱ の方は、fft 後に半サンプルシフトすることに該当する重みをかけることで、$\sin$ 項のキャンセルにつながる対称性が生じていると理解できます。ただ、DCT-Ⅲ の方で使用した重み

w(j) = \left\{ \begin{array}{ll}
\exp{\left( \frac{-\pi i}{2N}(j-1) \right)} & (1 \lt j \lt N), \\
\exp{\left( \frac{-\pi i}{2N}(j-1) -\pi i \right)} = \exp{\left( \frac{-\pi i}{2N}(j-1+2N) \right)} & (N+1 \lt j \lt 2N). \\
\end{array} \right.

が意味するところがいまいちピンとこないまま・・。もう少し理解しやすい式展開があるのかな。

もし「こう理解するといいよ」とか、他に何か参考になる資料などご存知でしたらコメント欄で教えて頂けると嬉しいです。よろしくお願いいたします。

1. 特に何も指定しなければ DCT-Ⅱ です。それぞれの違いについては Gilbert Strangy: "The Discrete Cosine Transform", SIAM Review, Vol. 41, No. 1, pp. 135–147 (1999) も参考になります。 ↩

2. 本家 FFTW も同じ。 see. FFTW: 1d Real-even DFTs (DCTs) ↩

3. それぞれの状況を「妻夫木」で解説しているので面白いですよ。 ↩