離散フーリエ変換から離散サイン変換までの式展開

はじめに

離散フーリエ変換から離散コサイン変換までの式展開 もやったので、ここはやっぱり離散サイン変換もやっておかないと年を越せない。

シンプルな DST-Ⅰ を取り扱います。MATLAB 関数もつけてます。

背景

以前、離散コサイン変換を使ってポワソン方程式を数値的に解きました。

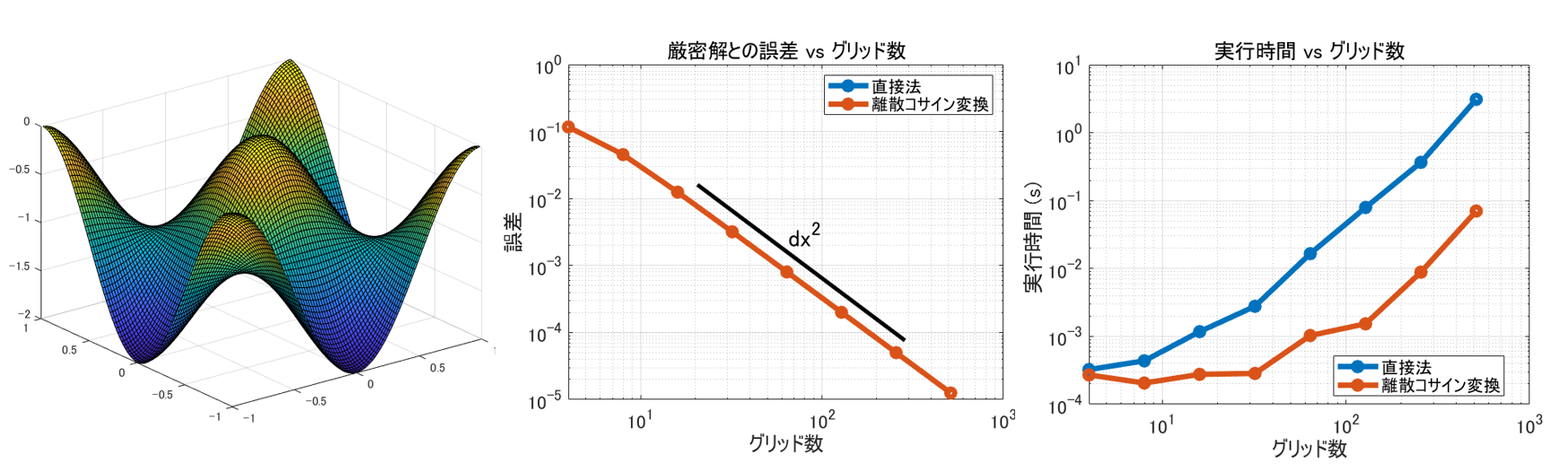
参照：Qiita: 離散コサイン変換でポアソン方程式を高速に解く

Neumann BC でない場合には、離散コサイン変換ではなく離散サイン変換を使うと便利。その例はまた次回。

と書いた通り、Dirichlet BC の時にも対応できるように、離散フーリエ変換 (fft) を使って離散サイン変換できるようになっておくといいことあるかも。

成果物

• mydst1.m： 離散コサイン変換（DST-Ⅰ）

MATLAB コード：mydst1.m

function b = mydst1(a)

arguments
   a (:,1)  
end

N = length(a);
% a(1), a(2), ..., a(N), 0, -a(N), -a(N-1), ..., -a(2),-a(1),0;
xx = [0;a;0;-flipud(a)]; % DST1
tmp = 1i*fft(xx)/sqrt((N+1)*2);
b = real(tmp(2:N+1));

以下、試しに実行してみた結果ですが、自分自身で逆変換になっていることが確認できます。

> x = rand(5,1);
> [x,mydst1(mydst1(x))]
ans =

    0.8085    0.8085
    0.7551    0.7551
    0.3774    0.3774
    0.2160    0.2160
    0.7904    0.7904

Which DST are you talking about?

離散コサイン変換 (DCT) に複数ある¹ように、FFTW では 4 つの離散サイン変換 (DST) があります²が、ここでは DST-Ⅰ を取り扱います。

DCT と同じくもともとのデータを周期信号へと拡張し、その信号に対して DFT を適用することと等価です。ただ、一周期分を偶対称とする DCT と違い、DST は奇対称とします。FFTW のレファレンスにも解説ページがありますが、DST-Ⅳ なんて拡張方法が興味深いですね。参考：Real even/odd DFTs (cosine/sine transforms)

DST-Ⅰ の場合、$x(1)$ ~ $x(N)$ を以下のように拡張します。

0, x(1),x(2), x(3), \cdots, x(N), 0, -x(N), -x(N-1), \cdots, -x(2), -x(1)

全長 $2N+2$ です。$j=0$ もしくは $j=N+1$ を中心に対称性を作ります。

定義式

fft の定義式は MATLAB 公式 doc ページ（高速フーリエ変換: fft）のものを使いますが、MATLAB に実装されているもの（PDE Toolbox にあります）の定義式とは少し変えて、FFTW のそれ（下記）から適当に変換しちゃいます。

y(k) = 2 \sum_{j=0}^{N-1} x(j) \sin{\left( \frac{\pi}{N+1} (j+1)(k+1) \right)}.

長さ $N$ の信号 $x$ に対しての離散フーリエ変換を $Y'(k)$、離散コサイン変換を $y(k)$ とおきます。

\begin{align}
{\rm DST-I} : y(k) &= \sqrt{\frac{2}{N+1}} \sum_{j=1}^{N} x(j) \sin{\left( \frac{\pi}{N+1} jk \right)}, \\
{\rm FFT} : Y'(k) &= \sum_{j=1}^{N} x(j) \exp{\left( \frac{-2 \pi i}{N} (j-1)(k-1) \right)}.
\end{align}

注: MATLABのベクトルは $0$ から $N – 1$ ではなく $1$ から $N$ で定義されるため、 和は $1$ から $N$ としています。DST-Ⅰは自身が自身の逆変換になるように正規化（？）しています。

xx = [0, x(1),x(2), x(3), \cdots, x(N), 0, -x(N), -x(N-1), \cdots, -x(2), -x(1)]

と周期信号へと拡張した長さ $2N+2$ のベクトル $xx$ に対しての離散フーリエ変換から式を展開していきます。$\cos$ 項が消えて $\sin$ 項のみが残るはず。

上の定義式から

\begin{align}
Y(k) &= \sum_{j=1}^{2N+2} xx(j) \exp{\left( \frac{-2\pi i}{2N+2} (j-1)(k-1) \right)}, \\
&= \sum_{j=1}^{N+1} xx(j) \exp{\left( \frac{- 2\pi i}{2N+2} (j-1)(k-1) \right)} 
+ \sum_{j=N+2}^{2N+2} xx(j) \exp{\left( \frac{- 2\pi i}{2N+2} (j-1)(k-1) \right)}. 
\end{align}

$xx(j) = - xx(2N-j+4)$ の関係を使うと、右辺の第 2 項は

\begin{align}
\sum_{j=N+2}^{2N+2} xx(j) \exp{\left( \frac{- 2\pi i}{2N+2} (j-1)(k-1) \right)} 
&= - \sum_{j=1}^{N+1} xx(j) \exp{\left( \frac{- 2\pi i}{2N+2} (2N-j+3)(k-1) \right)}, \\
&= - \sum_{j=1}^{N+1} xx(j) \exp{\left( \frac{ 2\pi i}{2N+2} (j-1)(k-1) - 2\pi i(k-1) \right)}, \\
&= -\sum_{j=1}^{N+1} xx(j) \exp{\left( \frac{ 2\pi i}{2N+2} (j-1)(k-1) \right)}.
\end{align}

と展開され、予定通り $\cos$ 項が消えそうです。$xx(1) = xx(N+2) = 0$ を使うと、

\begin{align}
Y(k) &= \sum_{j=2}^{N+1} xx(j) \exp{\left( \frac{- 2\pi i}{2N+2} (j-1)(k-1) \right)} - \sum_{j=2}^{N+1} xx(j) \exp{\left( \frac{ 2\pi i}{2N+2} (j-1)(k-1) \right)}, \\
&= -2i \sum_{j=2}^{N+1} xx(j) \sin{\left( \frac{\pi}{N+1} (j-1) (k-1) \right)}.
\end{align}

$k$ と $j$ について微調整すると

\begin{align}
Y(k+1) &= -2i \sum_{j=1}^{N} xx(j+1) \sin{\left( \frac{\pi}{N+1} jk \right)}, \\
&= -2i \sum_{j=1}^{N} x(j) \sin{\left( \frac{\pi}{N+1} jk \right)}.
\end{align}

DST-Ⅰ の定義

y(k) = \sqrt{\frac{2}{N+1}} \sum_{j=1}^{N} x(j) \sin{\left( \frac{\pi}{N+1} jk \right)},

と比べて、最終的に以下の通り DST-Ⅰ と DFT の関係が求まります。周期信号へと拡張した長さ $2N+2$ のベクトル $xx$ に対しての離散フーリエ変換 $Y(k)$ の $k=2$ から $k=N+1$ を下の式で変換したものが、求めたい DST の係数です。

y(k) = i \frac{Y(k+1)}{\sqrt{2(N+1)}}. 

これを実装した mydst1.m は上で紹介した通りです。

まとめ

離散サイン変換 DST-Ⅰ が計算できるようにはなりました。
次回は Dirichlet 境界条件のポワソン方程式でも解いてみましょう。

1. Gilbert Strangy: "The Discrete Cosine Transform", SIAM Review, Vol. 41, No. 1, pp. 135–147 (1999) も参考になります。 ↩

2. FFTW: 1d Real-odd DFTs (DSTs) ↩