最近Unityを始めてあまりのできのよさに感動を覚えつつ、物理演算とかがあまりにも手軽に行えるのでさすがに仕組みをまったく知らずに使うのは問題だろうと物理シミュレーションの勉強をしました。
ゴールとしていた、実際に動くものが作れたのでそのまとめです。
ただ、あくまで勉強が目的なので軽量化などはしていません。そのため、結構冗長な書き方をしていて実際に使うにはだいぶ重いです。
[2019.09.10 追記]
GitHubへのリンクを掲載していなかったので追記。
リポジトリの内容は以下から確認できます。
実際に作ったサンプル
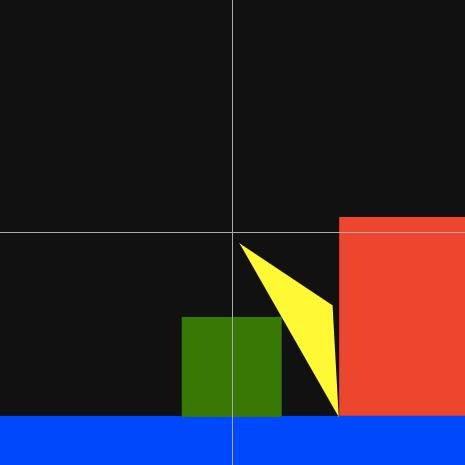
実際の動作サンプル
サンプルでは三角形と四角形、そして円との衝突判定を行い、衝突時に応答する部分まで作っています。
ここでは、この実装をしていくにあたって、躓いた点やメモなど自分が学んだことをつらつらと書いていきす。
シミュレーションパイプライン
さて、物理エンジンは与えられた剛体同士の衝突など、物理的な挙動を計算により導き出すエンジンです。
そのエンジンの仕組みに「パイプライン」があります。
一言で言うと、決まった工程(パイプ)を抜けると結果が導き出される、というものです。
詳細については、0から学習しているときにまとめた記事があるので、そちらを参照ください。
今回やったこと
今回の簡易2D物理エンジンの実装で、色々と理論を個別に実装しつつ、それらを組み合わせる形で実装しました。
そのため、その過程で必要になった理論やメモなどを順番に書いていきます。
慣性モーメントを求める
まず最初にやったのが、この 慣性モーメント を求める方法でした。
慣性モーメント(3次元だと慣性テンソル)から手を出したのは、2次元ではスカラー(float型などのいわゆる実数)で表せるのに対し、3次元だと行列になり、さらに参考にしていた書籍が2次元についてはあまり詳しく解説していなかったためです。
慣性テンソル?
慣性テンソルはベクトルを変換する行列?というような定義です。
(ちなみに慣性モーメントは 回転のしにくさ を表す量です。質量が 動かしづらさ を表すので、質量の回転版、と覚えておくと分かりやすいです)
なぜ2次元ではスカラー値なのに対し、3次元では行列となるのか。
それは、2次元ではZ軸を基準にしてしか回転しませんが、3次元の場合は任意の軸で回転することができます。
実際のものを想像してもらえば分かると思いますが、 どこを中心にして回すか によって 回りづらさ が変わります。
つまり中心にできる軸が無限にあるわけです。
それをいい感じに導き出してくれるのが慣性テンソル(行列)というわけです。
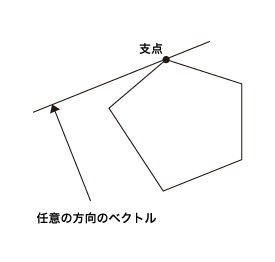
動作サンプル
画面をドラッグしてラインを引くと、中心からの距離とラインの長さ(力)に応じて、回転するスピードが変わります。
さらに、質量を設定するとそれだけ回転しづらくなるのが確認できるようになっています。
三角形の慣性モーメントの求め方
さて、問題の三角形の慣性モーメントの求め方ですが、理論的なところはまだあまり分かっていません( ;´Д`)
慣性テンソルは$I(Inertia・イナーシャ)$の記号を使い、以下の式が成り立ちます。
I_0 = mr^2
これは、物体のとある質点を取り出したとき、原点からの距離$r$の二乗と、質量$m$との積になる、という意味です。
そしてとある質点ではなく、「重心」の慣性テンソルの求め方が、(2次元の場合)以下になります。
三角形の質量を$m$、原点を始点とし三角形の各頂点を終点としたベクトルをそれぞれ$r_1, r_2, r_3$とします。
この三角形の慣性モーメント$I$は、以下の式で求められます。
I = \frac{1}{18}m(|r_1|^2 + |r_2|^2 + |r_3|^2 - r_2 \cdot r_3 - r_3 \cdot r_1 - r_1 \cdot r_2)
特に重心が原点にある場合は次のようになります。
I = \frac{1}{12}m(|r_1|^2 + |r_2|^2 + |r_3|^2)
上記の式はこちらの記事を参考にさせてもらいました。
この式を利用すれば、質量と頂点が分かれば慣性モーメント(慣性テンソル)を求めることができます。
これをプログラムにしたのが以下です。(実際につくったものからの抜粋です)
var v1 = this.vertices[0];
var v2 = this.vertices[1];
var v3 = this.vertices[2];
var v1len = vec2.lengthSqr(v1);
var v2len = vec2.lengthSqr(v2);
var v3len = vec2.lengthSqr(v3);
var v2v3 = vec2.dot(v2, v3);
var v3v1 = vec2.dot(v3, v1);
var v1v2 = vec2.dot(v1, v2);
var I = (1 / 18) * this.mass * (v1len + v2len + v3len - v2v3 - v3v1 - v1v2);
this.inertia = I;
円の慣性モーメントの求め方
円(円板)の慣性モーメントの求め方を参考にしました。
質量$m$、半径$a$の中心軸まわりの慣性モーメントの式は以下。
I = \int_0^a r^2 (\rho 2 \pi rdr) \\
一様な円板とすると \\
\rho = \frac{m}{\pi a^2} \\
となるので、 \\
I = \frac{1}{2}ma^2
衝突検出
次に、衝突検出の仕組みについて説明します。物理シミュレーションではこの衝突検出が一番重要な意味を持ちます。
なぜなら、物理シミュレーションはとても細かい数字で構成されるため、少しの誤差の積み重ねがとても大きなものになってしまうからです。
衝突検出には ミンコフスキー差 と呼ばれる理論と、 GJKアルゴリズム 、 EPA(Expanding Polythope Algorithm)法 というアルゴリズムが使われます。
ミンコフスキー差については、以前の記事に書いているのでそちらを見てください。
理論自体はとてもシンプルなものです。
さて、ミンコフスキー差の理論が分かっても、それをなんとかプログラムにしないとなりません。
線分と点との最短距離を求める
こちらもサンプルを作っています。

線分と点との最短距離は、その線分に垂線の足に当たる点か、あるいは線分の端になります。
これは実際に考えてみると分かると思います。
そしてそれをプログラムにするために参考にしたのが以下です。
線分と点との最短距離の求め方
線分ABの端点をそれぞれ$(x_0, y_0), (x_1, y_1)$とし、直線との最短距離を求めたい点を$(px, py)$とする。
まず点Pから線分ABに垂線を下ろし、その長さを計る。
まずは線分AB上の点を表すのに、パラメトリックに$(x_0 + dx * t, y_0 + dy * t)$で表すことにする。
ちなみに$dx, dy$はそれぞれ、$(x_1 - x_0), (y_1 - y_0)$と線分の長さに該当する値。
そして前述の媒介変数tは0〜1の間にある限り、線分AB上に点があることを示している。
(つまり、t == 1 のとき、点の位置は $x_1, y_1$ の位置になる)
そして垂線の足(*)$(tx, ty)$が線分上にない場合は、線分の端点$(x_0, y_0), (x_1, y_1)$のうち、垂線の足に近いほうの端点が最短距離となる。
- … 垂線の足は、直線に対して垂直に降ろした線との交差する点のこと。
解き方
垂線の足にあたる点は $(x_0 + dx * t - px, y_0 + dy * t - py)$ と書ける。
(点Pと上記で書いたパラメトリックに表した点との差分を計算することで垂線ベクトルを求めている)
そして線分と垂線のベクトルの内積は以下のように書ける。(ちなみに垂直なベクトルなので結果は0になる)
A \cdot B = (dx, dy) \cdot (x_0 + dx * t - px, y_0 + dy * t - py) \\
= (dx^2 + dy^2)t + dx(x_0 - px) + dy(y_0 - py)
このとき、
a = (dx^2 + dy^2) \\
b = dx(x_0 - px) + dy(y_0 - py)
と置くと、a == 0の場合はベクトルABが同じ点になることを示すため、線分ではなく点になり、点Pとは点と点の距離を求めればいいことになる。
そしてそうでなければ、上記式より$at + b = 0$となり、$t = -\frac{b}{a}$となる。
上記解き方は、こちらの記事を参考にさせて頂きました。
こちらのRubyプログラムをJavaScriptにすると・・。
/**
* 線分と点との最短距離を求める
*/
function distLine(x0, y0, x1, y1, px, py) {
var dx = x1 - x0;
var dy = y1 - y0;
var a = dx * dx + dy * dy;
if (a === 0) {
return Math.sqrt((x0 - px) * (x0 - px) + (y0 - py) * (y0 - py));
}
var b = dx * (x0 - px) + dy * (y0 - py);
var t = -(b / a);
if (t < 0.0) {
t = 0.0;
}
if (t > 1.0) {
t = 1.0;
}
var x = t * dx + x0;
var y = t * dy + y0;
return Math.sqrt((x - px) * (x - px) + (y - py) * (y - py));
}
サポート写像
上記の最短距離を求めるのは、ミンコフスキー差の理論で使うサポート写像を求める際に用います。
サポート写像は、任意の方向を向いているベクトルを決め、そのベクトル方向に一番遠い点を見つけ出す 関数 です。
そしてこのミンコフスキー差のサポート写像、ミンコフスキー差の図形を計算で求めなくても、ある簡単な方法で求めることができます。
ミンコフスキー差はふたつの物体を使って作る図形でした。
なので、それぞれの図形のサポート写像を求め、単純にそれを足すことで(正確には「ミンコフスキー差」なので引くことで)その写像を求める、というものです。
そして、この写像を求めるのに使われるのが内積です。
内積にはいくつかのとても便利な性質があり、それを利用します。
具体的にはこちらに少しだけまとめているので参照ください。
この内積の性質を利用すると、上記のサポート写像を求めることができます。
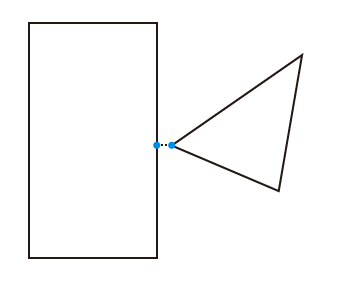
これのサンプルも上げているので見てみてください。
画面をドラッグすると、内積を使ってその図形の頂点の位置を、ドラッグで生成したベクトルに投影した点を表示します。
そしてこの理論をプログラムにする上で最後に必要になるのは、三角形の内側に点が存在するかどうかのチェックです。
三角形の内点かの判定
これ自体は、実は実装はとても簡単です。
理屈としては、三角形の各辺に対して点がどちら側にあるか、を判定すればいいのです。
辺に対してすべて内側の方向に点が存在すれば、それはつまり三角形の内側に点があることになります。
逆に、どれかひとつの辺でも反対側に点があればそれは三角形の中に点は含まれていないことを表しています。
これを実現しているのがこちらのサンプルです。
処理のコア部分を抜き出したのが以下です。
var originPos = this._originPos;
var v0 = this._foundPoints[0];
var v1 = this._foundPoints[1];
var v2 = this._foundPoints[2];
//三角形の各辺のベクトルを得る
var edge0 = vec2.sub(v1, v0);
var edge1 = vec2.sub(v2, v1);
var edge2 = vec2.sub(v0, v2);
//v0から見た辺の向きベクトルを得る
var ce0 = vec2.sub(v1, v0);
var ce1 = vec2.sub(v2, v0);
var CCW = 1;
//それぞれの辺の位置関係を外積によって確認し、
//時計回りか反時計回りかを判定
//時計回りの場合は、以後の判定のプラスマイナスを逆転させる
if (vec2.cross(ce0, ce1) < 0) {
CCW = -1;
}
//原点が三角形の辺の内側にあるかを判定
//3つの辺すべてに置いて内側という判定の場合は
//原点は三角形の内側に存在している
var cp0 = vec2.sub(originPos, v0);
if (vec2.cross(edge0, cp0) * CCW <= 0) {
return false;
}
var cp1 = vec2.sub(originPos, v1);
if (vec2.cross(edge1, cp1) * CCW <= 0) {
return false;
}
var cp2 = vec2.sub(originPos, v2);
if (vec2.cross(edge2, cp2) * CCW <= 0) {
return false;
}
return true;
さて、これで衝突判定に必要なプログラムが揃いました。
これを用いて衝突検出を行い、もし衝突が検出されたら、次は衝突点から 撃力(Impluse・インパルス) を求め、それを元に、衝突応答を計算してやります。
GJKアルゴリズム
衝突検出する方法はいくつかあるみたいですが、今回参考にしたのは「GJKアルゴリズム」と呼ばれるものです。
このアルゴリズムは前述した「ミンコフスキ差」を利用した衝突検出です。
ここからは、ミンコフスキ差を理解している前提で話を進めます。
まず、前提としてミンコフスキ差が原点を含んでいる場合はふたつの物体は衝突しています。
ここではこのミンコフスキ差が実際に原点を含んでいるかどうかを検出する方法を解説します。
それが「GJKアルゴリズム」です。
GJKアルゴリズムは前述の「サポート写像」を利用して衝突検出を行います。
こちらの記事がとても分かりやすく書かれているので、こちらを見てもらうと分かるかと思います。
EPA(Expanding Polythope Algorithm)法
GJKアルゴリズムと一緒に用いられ、衝突時の位置と距離(貫通深度)を調べる方法です。
基本的にはGJKアルゴリズムで使われる方法を用いて検出を行います。
これの詳細もやはり前述の記事がとても参考になるのでそちらを参照してください。
サンプル
三角形同士の衝突のサンプルを作りました。
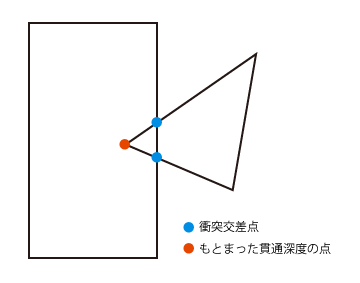
衝突点の座標を調べる
さて、前述までで貫通深度(どのくらいめり込んでいるか)と、どの方向に物体を動かしたらいいかの 衝突法線 (衝突が解消されるのに一番距離が短い方向)が分かりました。
ただ、これは方向と深度(ベクトルの長さ)が分かっただけで、実際に衝突している点はまだ分かっていません。
最初、前述までで求められるのかと思っていたので若干ハマりました。
衝突点の座標は、意外とコロンブスの卵的な感じで求めます。
まずざっくり手順を書くと、
- 物体を衝突法線方向に、貫通深度より若干長い距離移動させる
- その後、その移動後の物体同士の最接近点を求める
という手順です。
要は、一回衝突をなかったことにして、その上で一番近い点を求める、というのをやります。
実際は三角形同士の一番近い点を求めることになります。
こちらも手順をざっくり書くと、
- 三角形Aの全頂点と、三角形Bの各辺との最短点を求める
- 今度は逆に三角形Bの全頂点と三角形Aの各辺との最短点を求める
という手順です。
要は総当りで調べる、ってことですw
(本当なら、計算上除外できる点がいくつかあるので、そこは除外して速度アップなどをしますが、今回はそこまでの対応はしていません)
そして点と線分の最短点の求め方は前述の通りです。
この方法を使って、総当りで各点と各辺の最短距離を求め、その中で一番短い距離にある点が衝突点だ、というわけです。
言葉にするとわりとシンプルですが、これをプログラムにすると意外とめんどくさいです。
が、実装自体は分かりやすいでしょう。
ちなみに求めた衝突点は、それぞれの剛体のローカル座標に変換して保持しておきます。
理由は、衝突応答の計算時にローカル座標のほうが計算がしやすいためです。
さぁ、これで次の衝突応答(拘束の解消)ステージで必要な 貫通深度 、 衝突法線 、 衝突点の座標 が求まりました。
この情報を元に、衝突の応答を計算します。
衝突応答
検出応答のステージでは、上記の情報を元に、衝突の結果がどうなるのかを計算します。
まず、なぜ「拘束の解消」なのかと言うと、衝突した瞬間は次の時点(タイムステップ)では反発方向に移動することになります。
つまり、 反発方向に拘束されている 、と言い換えることができます。
今回、作っていく過程では書籍の中で説明されている公式をそのまま使いました。
いちおう、一般的に解いてからそれをプログラムに落としこむのですが、この一般式は読んで理解しているものの、説明できる理解度ではないので割愛します。
ここでは、出てきた公式とちょっとした説明にとどめます。
\begin{equation}
J =
\frac{-v_r(e + 1)}{1 / m_1 + 1 / m_2 + n \cdot[(r_1 \times n) / I_1] \times r_1 + n \cdot [(r_2 \times n) / I_2] \times r_2}
\end{equation}
記号の意味は以下の通り。
| 記号 | 意味 |
|---|---|
| $m$ | 質量 |
| $e$ | 反発係数 |
| $v_r$ | 物体Aと物体Bの相対速度 |
| $n$ | 衝突法線 |
| $I$ | 慣性モーメント(慣性テンソル) |
また、これを実際のプログラムにしたのが以下です。
var solverBodies = [];
var bias = ns.contactBias;
var slop = ns.slop;
var iteration = ns.iteration;
var rigidbodies = this._rigidbodies;
var pairs = this._pairs;
var timeStep = this._timeStep;
//ソルバー用プロキシを作成
//剛体の情報のうち、拘束の解消に使うものをコピー
for (var i = 0, l = rigidbodies.length; i < l; i++) {
var body = rigidbodies[i];
var solverBody = new ns.SolverBody(body);
solverBodies.push(solverBody);
}
//拘束のセットアップ
for (var i = 0, l = pairs.length; i < l; i++) {
var pair = pairs[i];
if (pair.contacts.length === 0) {
continue;
}
var bodyA = rigidbodies[pair.objA.id];
var solverBodyA = solverBodies[pair.objA.id];
var bodyB = rigidbodies[pair.objB.id];
var solverBodyB = solverBodies[pair.objB.id];
pair.friction = sqrt(bodyA.friction * bodyB.friction);
for (var j = 0, k = pair.contacts.length; j < k; j++) {
var contact = pair.contacts[j];
var cp = contact.contactPoint;
var dp = contact.depthPoint;
var r1 = vec3(vec2.sub(cp, solverBodyA.centerVert), 0);
var r2 = vec3(vec2.sub(cp, solverBodyB.centerVert), 0);
//いったん衝突法線を3次元ベクトルにする
var n = vec2.normalize(dp);
var normal = vec3(n, 0);
var velocityA = vec3.add(vec3(bodyA.velocity, 0), vec3.cross(vec3(0, 0, bodyA.angularVelocity * DEG_TO_RAD), r1));
var velocityB = vec3.add(vec3(bodyB.velocity, 0), vec3.cross(vec3(0, 0, bodyB.angularVelocity * DEG_TO_RAD), r2));
//2つの物体の相対速度を求める(V1 - V2)
var relativeVelocity = vec3.sub(velocityA, velocityB);
//接線ベクトル用変数
var tangent1 = vec3(0.0);
//接線ベクトルを求める
this._calcTangentVector(normal, tangent1);
var restitution = pair.typeNew ? 0.5 * (bodyA.restitution + bodyB.restitution) : 0.0;
// 衝突法線方向の計算
{
var axis = normal;
//rhs = Right Hand Side = 右辺
contact.constraints[0].jacDiagInv = 1.0 / (
(solverBodyA.massInv + solverBodyB.massInv)
+ vec3.dot(axis, vec3.cross(vec3.multiplyScalar(vec3.cross(r1, axis), solverBodyA.inertiaInv), r1))
+ vec3.dot(axis, vec3.cross(vec3.multiplyScalar(vec3.cross(r2, axis), solverBodyB.inertiaInv), r2))
);
contact.constraints[0].rhs = -((1 + restitution) * vec3.dot(relativeVelocity, axis));
contact.constraints[0].rhs -= (bias * max(0.0, contact.distance + slop)) / timeStep; // position error
contact.constraints[0].rhs *= contact.constraints[0].jacDiagInv;
contact.constraints[0].lowerLimit = -Number.MAX_VALUE;;
contact.constraints[0].upperLimit = 0.0;
contact.constraints[0].axis = axis;
}
//Tangent1
{
var axis = tangent1;
contact.constraints[1].jacDiagInv = 1.0 / (
(solverBodyA.massInv + solverBodyB.massInv)
+ vec3.dot(axis, vec3.cross(vec3.multiplyScalar(vec3.cross(r1, axis), solverBodyA.inertiaInv), r1))
+ vec3.dot(axis, vec3.cross(vec3.multiplyScalar(vec3.cross(r2, axis), solverBodyB.inertiaInv), r2))
);
contact.constraints[1].rhs = -vec3.dot(relativeVelocity, axis);
contact.constraints[1].rhs *= contact.constraints[1].jacDiagInv;
contact.constraints[1].lowerLimit = 0.0;
contact.constraints[1].upperLimit = 0.0;
contact.constraints[1].axis = axis;
}
//Warm starting
{
//あとで
}
}
}
//拘束の演算
for (var itr = 0; itr < iteration; itr++) {
for (var i = 0, l = pairs.length; i < l; i++) {
var pair = pairs[i];
var solverBodyA = solverBodies[pair.objA.id];
var solverBodyB = solverBodies[pair.objB.id];
//検出された衝突情報を元に撃力を計算
for (var j = 0, k = pair.contacts.length; j < k; j++) {
var contact = pair.contacts[j];
var cp = contact.contactPoint;
var r1 = vec3(vec2.sub(cp, solverBodyA.centerVert), 0);
var r2 = vec3(vec2.sub(cp, solverBodyB.centerVert), 0);
//Normal
{
var constraint = contact.constraints[0];
var deltaImpulse = constraint.rhs;
var deltaVelocityA = vec3.add(vec3(solverBodyA.deltaLinearVelocity, 0), vec3.cross(vec3(0.0, 0.0, solverBodyA.deltaAngularVelocity), r1));
var deltaVelocityB = vec3.add(vec3(solverBodyB.deltaLinearVelocity, 0), vec3.cross(vec3(0.0, 0.0, solverBodyB.deltaAngularVelocity), r2));
deltaImpulse -= constraint.jacDiagInv * vec3.dot(constraint.axis, vec3.sub(deltaVelocityA, deltaVelocityB));
var oldImpulse = constraint.accumImpulse;
constraint.accumImpulse = ns.clamp(constraint.lowerLimit, constraint.upperLimit, oldImpulse + deltaImpulse);
deltaImpulse = constraint.accumImpulse - oldImpulse;
solverBodyA.deltaLinearVelocity = vec2.add(solverBodyA.deltaLinearVelocity, vec2.multiplyScalar(constraint.axis, deltaImpulse * solverBodyA.massInv));
solverBodyA.deltaAngularVelocity += deltaImpulse * solverBodyA.inertiaInv * vec2.cross(r1, constraint.axis);
solverBodyB.deltaLinearVelocity = vec2.sub(solverBodyB.deltaLinearVelocity, vec2.multiplyScalar(constraint.axis, deltaImpulse * solverBodyB.massInv));
solverBodyB.deltaAngularVelocity -= deltaImpulse * solverBodyB.inertiaInv * vec2.cross(r2, constraint.axis);
}
var maxFriction = pair.friction * abs(contact.constraints[0].accumImpulse);
contact.constraints[1].lowerLimit = -maxFriction;
contact.constraints[1].upperLimit = maxFriction;
// Tangent
{
var constraint = contact.constraints[1];
var deltaImpulse = constraint.rhs;
var deltaVelocityA = vec3.add(vec3(solverBodyA.deltaLinearVelocity, 0), vec3.cross(vec3(0.0, 0.0, solverBodyA.deltaAngularVelocity), r1));
var deltaVelocityB = vec3.add(vec3(solverBodyB.deltaLinearVelocity, 0), vec3.cross(vec3(0.0, 0.0, solverBodyB.deltaAngularVelocity), r2));
deltaImpulse -= constraint.jacDiagInv * vec3.dot(constraint.axis, vec3.sub(deltaVelocityA, deltaVelocityB));
var oldImpulse = constraint.accumImpulse;
constraint.accumImpulse = ns.clamp(constraint.lowerLimit, constraint.upperLimit, oldImpulse + deltaImpulse);
deltaImpulse = constraint.accumImpulse - oldImpulse;
solverBodyA.deltaLinearVelocity = vec2.add(solverBodyA.deltaLinearVelocity, vec2.multiplyScalar(constraint.axis, deltaImpulse * solverBodyA.massInv));
solverBodyA.deltaAngularVelocity += deltaImpulse * solverBodyA.inertiaInv * vec2.cross(r1, constraint.axis);
solverBodyB.deltaLinearVelocity = vec2.sub(solverBodyB.deltaLinearVelocity, vec2.multiplyScalar(constraint.axis, deltaImpulse * solverBodyB.massInv));
solverBodyB.deltaAngularVelocity -= deltaImpulse * solverBodyB.inertiaInv * vec2.cross(r2, constraint.axis);
}
}
}
}
//計算結果を速度、回転に追加
for (var i = 0, l = rigidbodies.length; i < l; i++) {
var body = rigidbodies[i];
var solverBody = solverBodies[i];
body.velocity = vec2.add(body.velocity, solverBody.deltaLinearVelocity);
body.angularVelocity += solverBody.deltaAngularVelocity * RAD_TO_DEG;
}
これを元に、実際に動かしたサンプルはこちら
また、プログラム中で使っているベクトル計算(vec2とかvec3とか)は、自身のライブラリを使用しています。
(Githubで公開しています)
剛体の更新
さて、以上で各種必要な計算が終わりました。
あとは次のタイムステップでの剛体の位置や速度を更新してやり、ループ処理の中で順次更新されていけばめでたく物理シミュレーションに則した動きになる、というわけです。
作っていく上でハマったこととかメモ
とあるベクトルに垂直なベクトルを求める
垂直は、内積が0になるベクトル($A \cdot B = 0$)となるので、
$A = (a, b)$というベクトルがあるとすると、$B = (-b, a)$か$B = (b, -a)$という二通りのベクトルが考えられる。
例)
A = (2, 3) \\
A \cdot B = Ax * Bx + Ay * By = 0 より、 \\
2Bx + 3By = 0 \\
このとき、0になるのはB = (-3, 2) or (3, -2)となる。 \\
\\
2 * -3 + 3 * 2 = 0 \\
2 * 3 + 3 + -2 = 0
2次元での角速度
書籍やネットでの記事を参考にしていると、どうしても2次元の話と3次元の話が混在して、いざ実装しようとしたときに外積を求める式なのに、対応する変数がスカラーだったりと、式をどう解釈していいか混乱した。
角速度から、角運動量を求める公式は
L = r \times \omega
と、外積を使います。
が、2次元の場合は角速度($\omega$)はスカラーで表せるのと、計算を簡単にするために常にスカラーで保持していたため、外積?!となりました。(外積はベクトル同士の掛け算)
んで、2次元での角速度は、要は3次元でZ軸だけの回転と見なせることに気づき、以下のようにベクトルを生成して対応。
※スカラーは大きさのみを持つ量。言ってみれば実数。プログラムにしたらfloatとか。
//r … 物体の原点から接触点までのベクトル
// objA … 計算対象の物体A
// t … タイムステップ
var angularVelocity = vec3.cross(r, vec3(0, 0, objA.angularVelocity * t));
というふうにして、無理やり3次元ベクトル化して計算しました。
その他、外積が必要だけど3次元じゃねーよ!っていうのも、上記の理屈からZ軸の値を考えて追加して計算することでなんとかそれらしく実装。(ただ、もっといい実装は方法必ずあるけど、とりあえず理解が目的なのでこのへんで終了)