今度やる勉強会に向けて、剛体シミュレーションの概要をまとめていきます。
とはいえ、本格的に説明はできないので(理解不足で)、概要と今、自分が理解している範囲をまとめていきます。
知識としては、書籍を読んで把握した範囲なので若干偏りがあると思います。参考にした書籍は一番下に掲載しています。
(なので、なにか間違っている点などあればコメントいただけるとうれしいです)
こちらの理論などを元に、実際に2Dの物理エンジンを自作してみました。その過程で参考にしたものや躓いた点などをまとめた記事も書いているので、こちらもよかったら参考にしてみてください。→ 自作2D物理エンジンを作った話
概要
剛体シミュレーションは「パイプライン」という、各種の計算を行うステージを段階的に分けたものを通って、与えられた力(例えば重力)からの位置計算が行われます。
それぞれのステージの概要は以下の通りです。
シミュレーションパイプライン
剛体シミュレーションのパイプラインは以下のステージを通って最終的に剛体の状態が画面に反映されます。
- 剛体に外力を加える
- 衝突検出(ブロードフェーズ)
- 衝突検出(ナローフェーズ)
- 拘束の解消
- 剛体の位置・速度の更新
剛体に外力を加える
まず最初に、剛体に力を加えます。これがなければ画面は静止したままです。
基本的になにもしていなくても下方向、つまり重力が全剛体にかかることになります。
衝突検出(ブロードフェーズ)
外力を加えたあとは、それを元に徐々に状況が変化します。それに伴って剛体同士が衝突していないかを毎フレームごとにチェックしていきます。
しかし、すべての剛体を詳細に衝突判定するのはリアルタイムシミュレーションでは負荷が高すぎるため、まずはざっくりと「どれとどれが衝突している 可能性 がある」というのを検出します。これを ブロードフェーズ と呼びます。
衝突検出(ナローフェーズ)
ブロードフェーズで検出された剛体のペアを元に、それらが 本当に 衝突しているかを、このステージで詳細にチェックします。
そしてもし実際に衝突を起こしていたら、それを解消する必要があるため、次のステージである「拘束の解消」に情報が送られます。これを ナローフェーズ と呼びます。
拘束の解消
ナローフェーズで検出された剛体同士のペアを元に、「 どのように 衝突し、 どのくらい 重なっているのかの情報」から(この情報はナローフェーズで計算される)、跳ね返りや回転、速度に反映します。
剛体同士の重なりから、跳ね返り方向などが決定されます。
つまり逆を言えば、次の瞬間には そちらの方向にのみ 移動することができる= その軸に拘束されている、と言うことが出来ます。
そしてそれを解消するステージのため「 拘束の解消 」と呼ばれます。
剛体の位置・速度の更新
拘束の解消が出来たら、あとはそこで計算された速度などを剛体に反映することで、適切に跳ね返りや移動が反映されます。
ただ、これはあくまで物理演算をした結果でしかないので、それを画面に出力するにはOpenGLやWebGLなどの3Dをレンダリングできる環境を利用して画面に剛体を出力してやる必要があります。
◆
以上が剛体シミュレーションを行う上で必要なステージとパイプライン概要です。
以下からは、(自分が理解している範囲で)剛体シミュレーションの実際の方法を解説していこうと思います。
剛体シミューレションの理論
衝突検出(ブロードフェーズ)
ブロードフェーズについて簡単に説明します。
軸並行バウンディングボックス(AABB)
軸並行バウンディングボックスは(Axis Aligned Bounding Box - AABB)と略されることもあります。
下図のように、剛体全体を囲む領域を簡単な立方体で表し、その領域(ボリューム)を表す言葉です。
似たようなものに、バウンディングスフィア(立方体ではなく球体)や、通常のバウンディングボックス(Object Oriented Bounding Box - OOBB)があります。
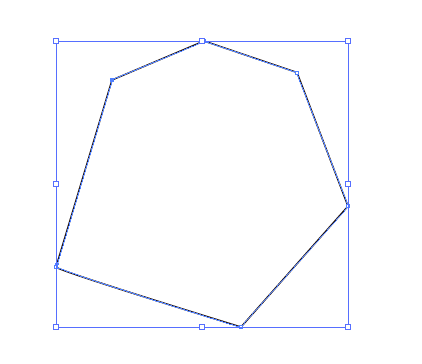
AABBイメージ
Adobe Illustratorの図形を囲むバウンディングボックス
AABBはブロードフェーズで利用されるもので、ざっくりとした衝突判定を行うのに適した形をしています。
衝突しているかどうかはXYZ軸それぞれについて最小値と最大値を比較し、ボックスが交差していないかをチェックするだけで判定ができます。
スイープ&プルーン
なんだか変な名前ですが、概念としては判定したい軸に対して剛体の各頂点を投影し、それぞれの端点を比較することで衝突を検知するものです。
AABBによる判定も同じ理論で判定しており、XYZ軸に対してスイープ&プルーンを実行している、といってもいいでしょう。
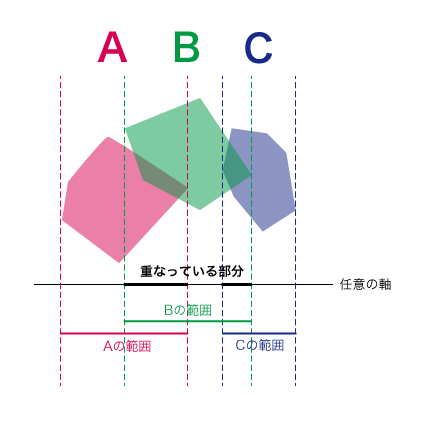
大まかな概念は以下の図のようになります。
任意の軸をひとつ取り出し、そこに対しての重なりを調べることで衝突判定を行います。
例はあくまで2次元上での重なりなので3次元では重なっているとは限りません。
そこで、ひとつの軸で重なりが検出されたら他の2軸も同様に衝突判定を行い、すべてが重なっていたら衝突している可能性があるペアとして剛体同士を登録します。(プログラム的にはペアを表す構造体を用意し、そこに剛体の情報と衝突情報を保存して配列で保持します)
これを 3軸スイープ&プルーン と呼び、基本的に取り出す軸はXYZ軸になります。
次のナローフェーズではここで検出されたペア情報を入力として受け取り、さらに詳細な衝突検出を行います。
重なりの調べ方
ここでの重なりの検出は、おそらくベクトルの内積を用いて判別するものと思います。
原点からの各頂点の位置をベクトルとし、軸に対して内積を取る(つまり投影させる)ことで、それぞれの位置が算出され、そしてそれを元に重なり具合を判別する、というものです。(内積については割愛します。ここでの内積の使い方はこちらを参照してください)
サンプル
実際に内積を使って位置を算出するサンプルを作ってみました。
以上でブロードフェーズの解説は終わりです。
書籍ではさらに、剛体が多数ある場合にそれらを効率よく衝突検出する部分も書いてありましたが、検知する対象の絞り込みになるのでいったん割愛します。(もしかしたらどっかで書くかも)
ちなみにキーワードとしては「ノード ツリー AABBツリー」など、剛体をグループに分けノードとして扱う、というものです。
衝突検出(ナローフェーズ)
さて、続いてナローフェーズの解説です。
ナローフェーズではブロードフェーズで得られた 衝突の可能性のある剛体のペア を入力として受け取り、それぞれの剛体同士についてさらに詳細に衝突検出を行います。
検出に用いる手法・理論は ミンコフスキ差 と 分離軸 のふたつです。
ミンコフスキ和
まず最初に ミンコフスキ和 について簡単に解説します。
ミンコフスキ和とはふたつの凸多面体において以下を満たすものです。
\begin{equation}
A + B
=
\{x + y : x \in A, y \in B\}
\end{equation}
ミンコフスキ和は物体Bで物体Aの上をなぞった形状
ミンコフスキ和は、図で示した通り各物体の頂点同士を合計したあとに現れる図形です。
イメージとしては、物体Bの原点を物体Aの辺上に合わせてぐるっと一周させたときにできる軌跡、と考えると分かりやすいと思います。
ミンコフスキ差
さて、実際に衝突検出に用いられるのはこちらの「差」のほうです。
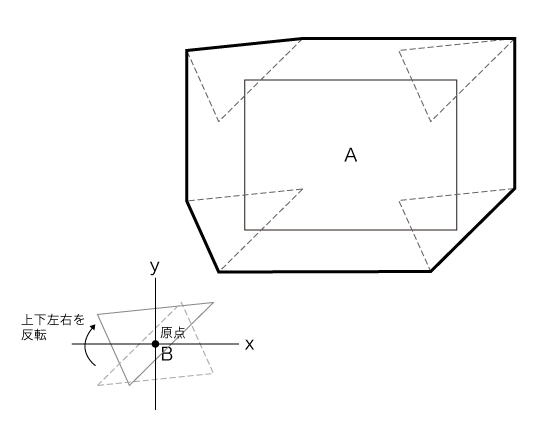
定義はすっとばして結論だけを書くと、前述の物体Bの上下左右を反転し、それのミンコフスキ和を取るだけです。図にすると以下のようになります。
ミンコフスキ差は、物体Bを反転(マイナス)して和を取ったものに等しい
さて、ミンコフスキ差の仕組みは分かったと思いますが、これがなぜ衝突判定に用いられるのでしょうか。
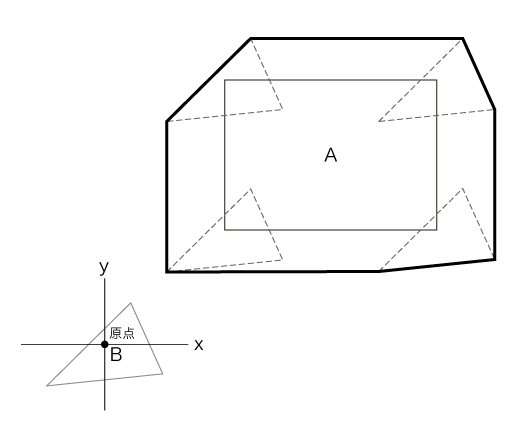
その答えが次の図です。
図はミンコフスキ差の形状を物体Bのローカル座標系に移動して座標系の軸を表示したものです。
図で見ると分かりますが、衝突していない場合はミンコフスキ差の形状は物体Bのローカル座標の原点を通っていませんが、衝突している場合は原点を含んでいることが確認できます。
つまり、ミンコフスキ差が物体Bのローカル系において原点を通る場合に、物体同士は衝突している、と見ることができるわけです。
ミンコフスキ差の衝突判定
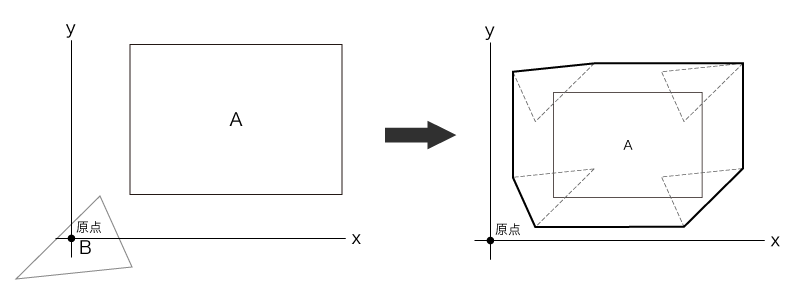
物体Bのローカル座標系で表したミンコフスキ差の図。衝突していないので原点は含んでいない
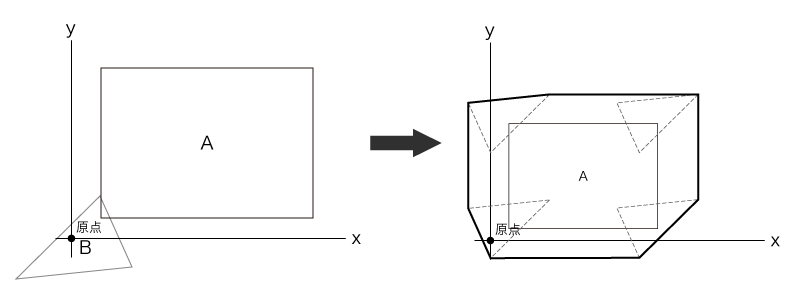
こちらは衝突しているため、ミンコフスキ差の図形が原点を含んでいる
サンプル
ミンコフスキ差を利用した詳細な衝突判定のサンプルを作りました。
貫通深度
ミンコフスキ差を使うと衝突しているかを判定することができるのは説明した通りです。
実はミンコフスキ差はさらに有用な情報を与えてくれます。
衝突を検知した際、衝突後どちらの方向に剛体を動かしたら効率的に衝突を解消できるかの方向も計算しなければなりません。
ミンコフスキ差はその方向や距離も教えてくれます。
原点から一番近いミンコフスキ差の辺を調べればその点が算出できます。
それを 貫通深度 と呼びます。原点からこの点までのベクトルが衝突を解消する最短距離かつ方向となります。
原点からミンコフスキ差までの最短の距離などの求め方はこちらの記事が参考になります。
(「GJKアルゴリズムの原理」あたりです)
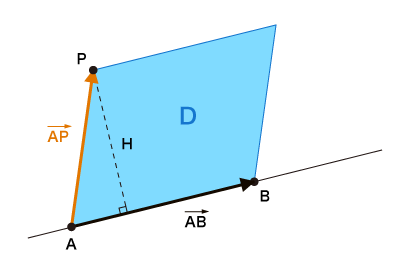
図の青い平行四辺形の面積は、ベクトルの外積から求めることができます。
D = \vec{AB} \times \vec{AP}
そしてDは平行四辺形なので、
H * |AB| = D
が成り立つので、Hは以下の式から求めることができます。
点と直線の距離H = D \; / \; |AB|
[2014.07.24 追記]
ちなみに、上記記事のGJKアルゴリズムの原理で原点との判定を行っていますが、ミンコフスキ差の図形を使って解説しているために若干混乱しますが、実際にプログラムを行う段階ではその図形を表す式はありません。
あくまでサポート写像を用いて、それぞれの点を計算していき、3点見つかったタイミングで三角形を形成し、以後計算を繰り返す、という形になります。
分離軸の理論
次に説明するのは、これもまた衝突検知に用いられる理論で、 分離軸の理論 と呼ばれるものです。
分離軸の理論を簡単に言うと、空間に任意の軸をひとつ取り、その軸に対して剛体の各頂点を投影します。
そしてその重なりを調べることで、衝突を検知するものです。(おそらくスイープ&プルーンも同じような仕組み)
そして分離軸の理論では、2つの物体が重なっていない場合「 それぞれの物体の射影が重なっていない軸が空間中にひとつ以上存在する 」という理論です。
逆に言えば、もし仮に2つの物体が重なっている場合は、分離軸は空間上にひとつも存在しない、とも言えます。
分離軸の図解
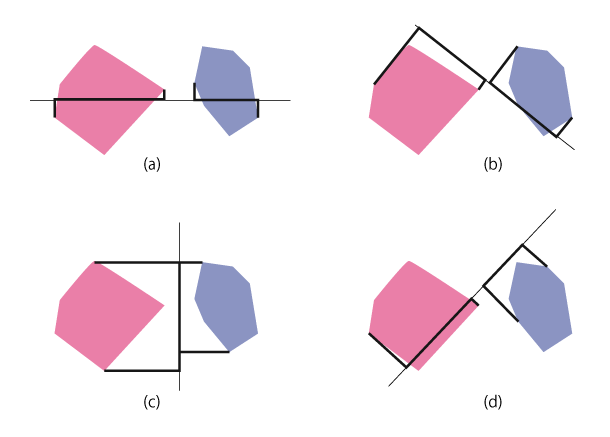
(a), (b), (d)はそれぞれ軸上の射影は重なっていない。これらを「分離軸」と呼びます
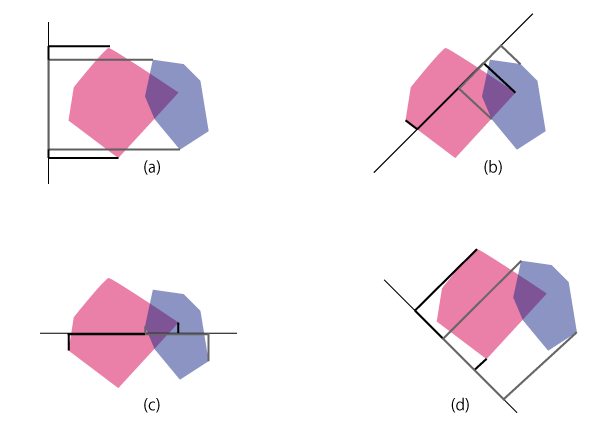
どの軸上の射影も重なっているため、分離軸として使える軸が存在しないことが分かります
分離軸を使った衝突検出
上記の例の軸は完全に任意の軸です。しかし、実際のリアルタイムシミュレーションで、どこにあるか分からない分離軸を適当に選んで探していてはいつまでたっても処理が終わりません。
しかし、前述したミンコフスキ差の図形を使うと解決できます。
ミンコフスキ差の衝突検出は、ふたつの物体の重なりを元に図形を描き、それが原点を含むかどうかで衝突判定を行うものでした。
これは言い換えれば、原点が該当の物体を衝突しているかをチェックすることに他なりません。
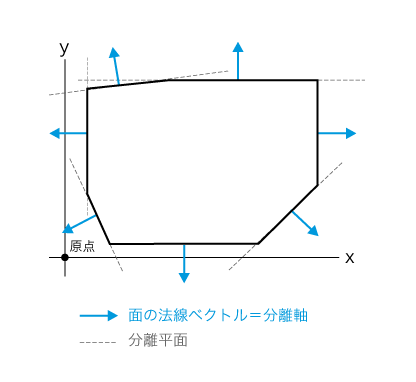
つまり、ミンコフスキ差の描く各面を分離平面として、各平面と原点との衝突判定を行うことで衝突の検出が可能となります。
図にすると以下のようなイメージです。
接触法線ベクトルと貫通深度の計算
前述の理論を使うことで、物体の衝突は検出できます。
しかし、実際には衝突をただ判定しただけでは足りません。
リアルタイムの物理演算の微小時間を考えると(例えば1フレーム)、現実世界とは異なり物体同士が重なる瞬間があります。これをめり込みといい、次のフレームではそれを解消するよう力を与えないとなりません。
そのため、衝突検出だけでなく、どうめり込みを解消するのか、方向と距離を求める必要があります。
それが 接触法線ベクトル と 貫通深度 です。
結論から言うと、ミンコフスキ差で出てきた「原点」をミンコフスキ差の外に出す処理です。
そしてそれには、原点からもっとも近いミンコフスキ差の面の法線ベクトル方向に移動することで求めます。この法線を、 接触法線ベクトル(Contact normal) と呼びます。
そして、「原点」からその面の表面までの距離を 貫通深度 と呼びます。
接触多面体(Contact manifold)
通常、ある程度安定した状態では物体は点ではなく面で接することになります。
しかし衝突点を求め、それに対して衝突を解消するとその点において撃力が働き、別の方向に物体は回転しようとします。
すると安定しているはずのボックスは別の点がめり込み、さらにそこでも撃力が発生し、別の回転が生まれます。
結果、安定しているはずのボックスは常に撃力が至るところで発生し小刻みに動くことになってしまいます。
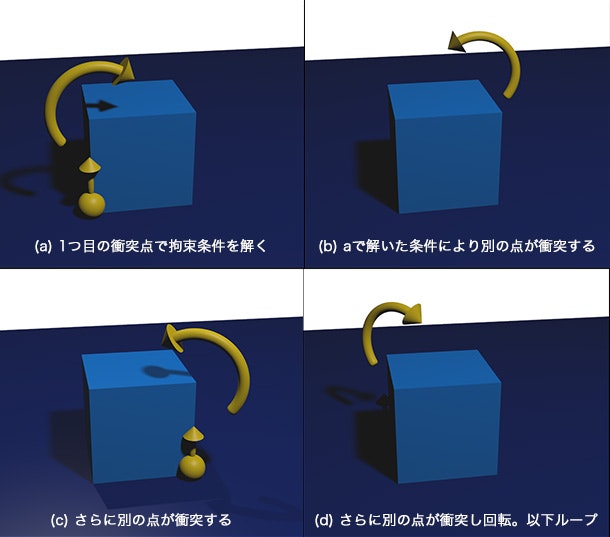
それをイメージにしたのが下の図です。
球が衝突点、矢印が撃力の方向、丸い矢印が回転方向です。
このように衝突が繰り返され、安定しなくなります。
これは本来は衝突「点」ではなく、衝突「面」として解決しなければいけないところを、点のみで解決しようとするために起こる問題です。
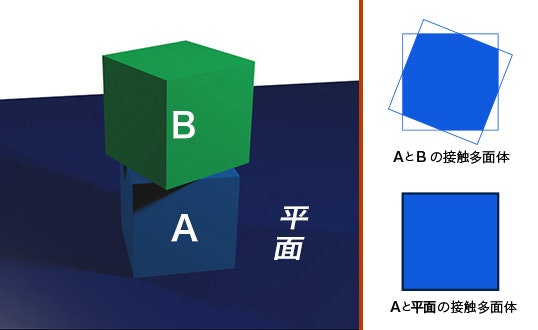
これを解消するために、面での解決を試みます。ちなみにこの衝突面を「接触多面体」と呼びます。
これは、接触しているふたつの物体の面が多面体になるためにこう呼ばれます。
この問題を解決するために複数の衝突点をまとめて解消することで安定を図ります。
つまり、図の(a)〜(d)の間で発生した点をそれぞれ保持しておき、すべての状態を解消することで安定させる、という手法です。
局所的に見ると問題の解決にはなりませんが、シミュレーションを重ね、計算回数が増えることで徐々に安定するようになります。
拘束の解消
前述までで、衝突検出と衝突点の判別が出来ました。
これらの情報を入力として、次のステージは 拘束の解消 です。
まず、なぜ「拘束の解消」なのか。
衝突した瞬間は次の時点(タイムステップ)では反発方向に移動することになります。
つまり、その方向に拘束されている、と言い換えることができます。
拘束条件を以下の式で表します。
C(x) = 0
今、ふたつの剛体($P_1$と$P_2$)が衝突しているとすると、衝突点はその空間座標で$(P_1 - P_2) \cdot n = 0$となり、同じ座標の衝突点の差分は0となります。(同一座標であれば衝突点はひとつとなり、同じ座標同士の差分となるため)
ここで$n$は衝突時の反発方向のベクトルです。
つまり、反発方向に拘束されていると見ることができます。
さらに、現実世界ではふたつの物体はめり込みません。(柔らかい物体などはめり込みますが、局所的に見ればめり込んでいません)
そのため、次の時点ではそれ以上めり込みは発生しません。その拘束条件が$C(x) = 0$となるわけです。
つまりこれは衝突しているふたつの剛体の相対速度が0になれば次の時点ではめり込まないので、これを解きます。
従って、相対速度が0になるような衝突点の撃力を求め、並進運動と回転運動に分解して各剛体に力を加えればいいことになります。
実際にはこれでは衝突した瞬間、相対速度が0になるのでまるでくっついたように見えてしまいます。
通常はぶつかった物体同士は、今度は離れる方向に移動するのが自然です。
これは 反発係数 を導入し、相対速度が0以上(プラスの方向)になるように補正することで対応できます。
場合によっては物体が振動するような状態になり、なかなか動きが収束しない場合があります。
物体同士が安定しているときは前回検出された衝突点情報を更新していく形になります(衝突点が変化せず、一定のため)。
解決策としては、前回検出された撃力に力を蓄積し、均一化することで安定化を図っていきます。
さて、撃力の計算についてはこちらの記事が参考になります。
この記事を元に、自分なりに理解した部分を書いていきます。
(あくまで頭の中の整理のために書いているので、勘違いもあるかと思います)
参考記事と同様、ふたつの物体が衝突するシーンを正面衝突に限定します。
正面衝突なのでそれぞれの速度ベクトルは正反対のベクトルになります。
それをそれぞれ$V_1$、$V_2$とします。
(ちなみに正面衝突以外では法線方向の成分を取り出せばいいので、$(V \cdot n)n$の内積を使って計算できます。内積についてはこちらの記事が参考になると思います)
そして衝突時の相対ベクトルを$\Delta V_{12} = V_2 - V_1$とすると、衝突後の相対ベクトル$\Delta V'_{12} = V'_2 - V'_1$は、反発係数$e$を用いて
\Delta V'_{12} = -e \Delta V_{12}
と表せます。これを変形すると、
\begin{equation}
e
=
\frac{V'_1 - V'_2}{V_2 - V_1}
\end{equation}
となります。
$V'_1$と$V'_2$が求めたい衝突後の速度なので、
力 f = ma =
\int_{\Delta t} fdt = \int_{\Delta t} m\frac{dV}{dt}dt = m\Delta V \\
\Delta V = \frac{f\Delta t}{m} \\
撃力 J = f \Delta t
を使って、
\Delta V = \frac{f \Delta t}{m} = \frac{J}{m}
より、
V'_1 = V_1 + \Delta V = V_1 + \frac{J}{m_1}
V'_2 = V_1 + \Delta V = V_2 + \frac{J}{m_2}
ちなみに$m$はそれぞれの物体の質量です。
これを反発係数$e$について解くと、
e = \frac{1}{V_2 - V1}\left(V_1 + \frac{J}{m_1} - V_2 + \frac{J}{m_2} \right)
そしてこれを、撃力である$J$について解くと、求めたい撃力が求められます。
J = (1 + e)\frac{m_1m_2}{m_1 + m_2} \Delta V_{12}
ただこれは並進運動のみの式なので、これに回転運動を加えると、回転運動は慣性テンソルと重心から衝突点までの距離で計算できるので、
J = (1 + e)\left(\frac{m_1m_2}{m_1 + m_2 + m_1m_2\left(\left(I^{-1}_1\left(r_1 \times n\right)\right) \times r_1 + \left(I^{-1}_2 \left(r_2 \times n \right)\right) \times r_2 \right) \cdot n} \right)\Delta V_{12}
として求めることができます。
剛体の位置・速度の更新
あとで書く。