概要
最近は機械学習、ディープラーニングの話題が非常にたくさん出てきていますね。
ということで、そろそろしっかり機械学習、ディープラーニングに手を出しておかないとということで勉強を始めました。
が、まずその前に、(観測している範囲だと)大体Pythonを使って作られている・説明されているケースが多いので、機械学習向けとしてPython入門って形でメモを書きたいと思います。
自分自身、あまりPythonに触れたことがないのでたんに備忘録ですw
ちょっとした文法だったり、ディープラーニングに用いられるライブラリの使い方だったり、がメインです。
なので、がっつりPython入門したい! という人には不向きな記事になってます。
なお、いくつかの関数についてはこちらの本を参考にさせてもらっています。
ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装
import
オライリーのこちらの本(ゼロから作るDeep Learning ―Pythonで学ぶディープラーニングの理論と実装)を読んでいても、やはりPythonによる説明がなされています。
その中でも「NumPy」というライブラリが、ディープラーニングを実装していくにあたってとても有益なことが伝わってきます。
(行列の演算や、ベクトル、そしてテンソルなど様々な「配列」表現をそつなくこなしてくれるすばらしいライブラリです)
そんなライブラリ(モジュール)たちを読み込むのが「import」です。
import numpy
# 配列を生成する
x = numpy.array([0.1, 0.2])
みたいに記述します。
asで別名をつける
numpyくらいなら大したタイプ数ではないですが、長いモジュール名の場合、毎回それを記述するのはめんどくさいですよね。
ということで、asを使って別名をつけることができます。
import numpy as np
# 配列を生成する
x = np.array([0.1, 0.2])
fromを使ってクラス(や関数)だけをimportする
importはモジュール(Pythonの場合はモジュールはファイル単位)を読み込むものでした。
しかし、場合によってはモジュールすべてを読み込むのではなく、そのモジュールの中にある特定のクラスだけを利用したい、というケースもあると思います。
しかし、通常のimportではモジュールすべてを読み込んでしまうため、moduleName.moduleClassのようにアクセスしないとならなくなります。
例えば以下のようなモジュールがあったとします。
class classTest:
def print_test(self):
print('this is test.')
これを別のファイルから読み込んで扱うには以下のようにします。
import classExample
c = classExample.classTest()
c.print_test() # => this is test.
これでも問題なく動きますが、もしこのclassTestクラスを何回も記述しないとならないとしたらめんどくさいですよね。
そこでclassTestを直に呼び出せるようにするのがfromです。
上記を書き直してみると以下のようになります。
from classExample import classTest
c = classTest()
c.print_test() # => this is test.
だいぶ短くなりました。
from [HOGE] import [FOO], [BAR]で複数読み込む
fromによって関数だけを読み込むことができました。
しかし、場合によってはひとつだけではなく、複数読み込みたい場合があると思います。
その場合は、importのあとの指定で、カンマ(,)区切りで列挙することで同時に読み込むことができます。
from hoge import foo, bar
foo()
bar()
フォルダ階層を使って読み込み
フォルダ名はそのままモジュールの階層になります。
なので、例えば以下のようにファイルを配置していた場合、
$ tree .
.
├── load_sample.py
└── utility
└── sigmoid.py
これを以下のようにして読み込むことができます。
from utility.sigmoid import sigmoid
import numpy as np
x = np.array([0.1, 0.2])
y = sigmoid(x)
print(y)
import numpy as np
def sigmoid(x):
return 1 / (1 + np.exp(-x))
* を使ってまとめて読み込む
ちなみに、以下のように記述することで該当モジュールの関数をまとめて読み込むことができます。
from moduleName import *
モジュール読み込みでハマる
これは、実際にコードを書いていてプチハマりをしたのでメモとして残しておきます。
(Python詳しかったら多分、なんてことはない話です)
モジュールの読み込みパスを追加する
少しだけ話しがそれますが、以下のようにすることでモジュールの検索範囲(パス)を広げることができます。
import sys, os
sys.path.append(os.pardir) # => 文字列「".."」 が追加される
sys.pathにモジュールの検索対象パスが配列で定義されているので、親のパス("..")を追加することで、親ディレクトリも検索対象にしてくれる、というわけですね。
さてここで、".."は「どこ」を指すのか。これが今回ハマった点です。
結論から言うと「実行時のディレクトリ」です。
つまり、以下のような構造になっていて、
$ tree .
├── hoge
│ ├── foo
│ │ └── sample.py
│ ├── common
│ │ └── functions.py
from common.functions import *
# do anything
hoge> $ python hoge/sample.py
のようにhogeディレクトリから実行したとしましょう。
すると、この".."は**hogeの「親」**を指すことになります。
よって、意図しているディレクトリ(上の例だとhogeディレクトリ)が含まれず、結果としてModuleNotFoundエラーが出る、というわけです。
なので、以下のように実行すると問題なく実行できます。
hoge/foo> $ python sample.py
lambda式を使う
Pythonも、関数をオブジェクトとして扱うことができます。
ラムダ式は以下のように記述します。
def tangent_line(f, x):
d = numerical_diff(f, x)
y = f(x) - d*x
return lambda t: d*t + y
classを定義する
他言語と同様、Pythonにもクラスがあります。
クラスは以下のようにして定義します。
class Hoge:
def __init__(self, a, b, c):
self.a = a
self.b = b
self.c = c
def Foo(self):
print(self.a)
h = Hoge(1, 2, 3)
print(h.Foo()) # => 1
class Hoge:がクラスの宣言部分です。
他の言語と少し違う点は、メソッドの第一引数にselfを指定する点でしょうか。
それ以外は基本的に他言語と同様です。
NumPyを使う
さて、Python入門と言いながらライブラリの使い方です。
DeepLearningでは多用するということと、Pythonがなぜ利用されるのか垣間見れるのでPythonを使う上でいいヒントになるかなと思ったのがその理由です。
NumPy配列
Pythonにも当然、他のプログラムと同様「配列」があります。
が、DeepLearningではNumPyの配列を利用します。
というのも、NumPyの配列は多次元配列に対応し、さらにとても簡単に配列に対しての操作を行うことができるようになっているためです。
さらに、いわゆる「行列」の積の計算も簡単に行うことができます。
例えばこんな感じ。
import numpy as np
X = np.array([[1, 2], [3, 4]])
Y = np.array([[10, 20], [30, 40]])
A = np.dot(X, Y)
print(A)
# [[ 70 100]
# [150 220]]
NumPyの配列生成
NumPyの配列は以下のように、Pythonの配列を渡して生成します。
import numpy as np
x = np.array([1.0, 2.0, 3.0])
print(x)
# [ 1. 2. 3.]
print(type(x))
# <class 'numpy.ndarray'>
NumPyの算術計算
次に、配列同士の算術計算です。
以下のように、通常の四則演算が定義されています。
import numpy as np
x = np.array([1.0, 2.0, 3.0])
y = np.array([2.0, 4.0, 6.0])
print(x + y)
# array([ 3., 6., 9.])
print(x - y)
# array([-1., -2., -3.])
print(x * y)
# array([ 2., 8., 18.])
print(x / y)
# array([ 0.5, 0.5, 0.5])
それぞれの要素同士で四則演算がなされているのが分かります。
なお、大事な点として配列の要素数が一致している必要があります。
もし違う要素数同士で計算を行うと、以下のようにエラーが表示されます。
# 上の実行に続けて以下を実行
z = np.array([1.0, 2.0])
x + z
# Traceback (most recent call last):
# File "<stdin>", line 1, in <module>
# ValueError: operands could not be broadcast together with shapes (3,) (2,)
計算のブロードキャスト
ちなみに、以下の計算はエラーが出ません。
import numpy as np
x = np.array([1.0, 2.0, 3.0])
print(x / 2.0)
# array([ 0.5, 1. , 1.5])
スカラーとの計算でも、それぞれの要素分に拡張されて(ブロードキャストされて)計算が行われます。
NumPyのN次元配列
通常の配列と同様、配列を入れ子にすることによって多次元配列を定義することができます。
import numpy as np
A = np.array([[1, 2], [3, 4]])
print(A)
# [[1 2]
# [3 4]]
print(A.shape)
# (2, 2)
print(A.dtype)
# dtype('int64')
サンプルではA.shape = [2, 2]という結果から、2次元配列になっているのが確認できるかと思います。
また、最初の例のように、多次元配列同士も四則演算を行うことができます。
# 上記に続けて以下を実行
B = np.array([[3, 0], [0, 6]])
print(A + B)
# array([[ 4, 2],
# [ 3, 10]])
print(A * B)
# array([[ 3, 0],
# [ 0, 24]])
要素へのアクセス
要素へのアクセスは通常の配列と違いはありません。
print(A[0])
# array([1, 2])
特殊な配列操作
flattenで1次元配列へ変換
個人的に、NumPyを使う理由はこれか、と思ったのがとても柔軟な配列操作です。
例えば、以下のようにすることで1次元配列に変換することができます。
print(A)
# array([[1, 2],
# [3, 4]])
A2 = A.flatten()
print(A2)
# [1 2 3 4]
機械学習において、画像は長大な1次元配列として扱うこともあるので、これはとても便利な機能です。
配列を要素アクセスに使う
さらに、NumPyでは以下のように配列で要素を指定することができるようになっています。
X = np.array([10, 20, 30, 40, 50, 60, 70, 80, 90 ])
print(X[np.array([0, 3, 5])]) # index 0, 3, 5の要素を取り出す
# array([10, 40, 60])
bool型で取り出す要素を指定する
最後に、NumPy配列に対して比較を行うと、対象の要素がそれを満たす場合はTrue、そうでない場合はFalseを含む配列が生成されます。
そしてさらにそれを元に、マスクとして作用させることもできます。
と、言葉で書いても分かりづらいので実際のコードを見てみるとすぐに分かるかと思います。
X = np.array([10, 20, 30, 40, 50, 60, 70, 80, 90 ])
mask = X > 50 # Xの配列の中から、50より上の要素を調べる
print(mask)
# [False False False False False True True True True]
mask_X = X[mask] # 得られた配列をマスクとして作用させて、該当の要素を抜き出す
print(mask_X)
# [60 70 80 90]
DeepLearningでは配列ごとに処理をすることが非常に多く、こうして柔軟に配列にアクセスできるのはとても便利ですね。
NumPyを使ってDeepLearningを実装するのがよく分かる機能です。
matplotlibでグラフを表示する
さて最後に、matplotlibライブラリの簡単な使い方を書いて終わりにしたいと思います。
これを書く理由は、DeepLearningを進めていく上で現在の状態をグラフ化し、状況を視覚化することで見えてくるものがあるからです。
NumPyを使うととても簡単に、行列やベクトル、テンソルの計算ができることが分かりました。
ただ、数値だけを見ていても動作がイメージしづらかったり、どういう結果になるのかグラフで知りたいケースもあると思います。
そしてmatplotlibを使うことでそれを簡単に実現できます。
numpy.arrayを渡すとそれをグラフ化して表示してくれるとても便利なライブラリです。
まずはimport。
import matplotlib.pyplot as plt
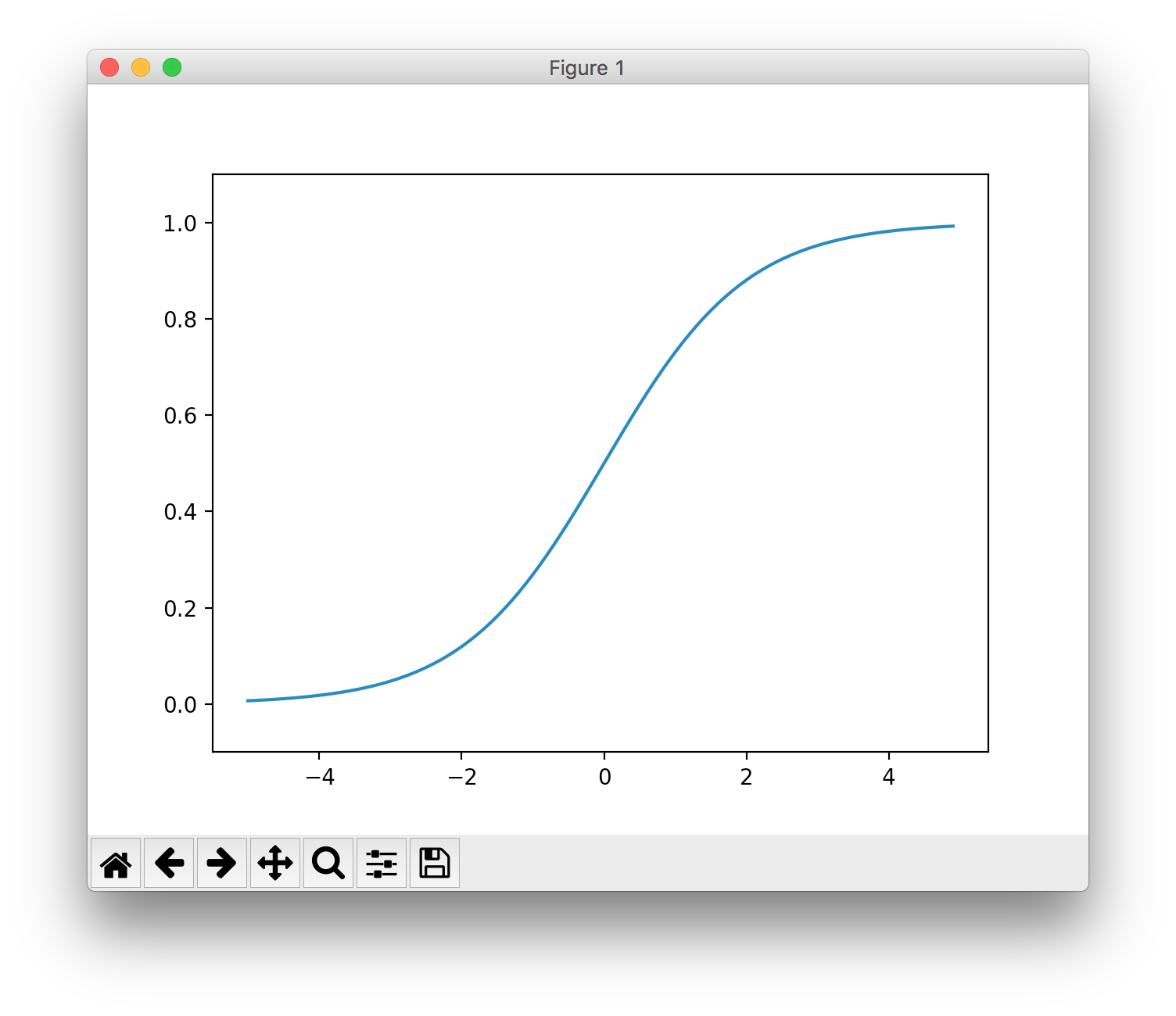
試しに、ディープラーニングで使われる「シグモイド関数」を描画してみます。
import numpy as np
import matplotlib.pyplab as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.arange(-5, 5, 0.1)
y = sigmoid(x)
plt.plot(x, y)
plt.ylim(-0.1, 1.1)
plt.show()
これを実行すると以下のようなグラフが表示されます。
さて、他書式などを見てみましょう。
以下のようにすることで、ラインのスタイルなどを変更することができます。
import numpy as np
import matplotlib.pylab as plt
x = np.arange(0, 6, 0.1)
y1 = np.sin(x)
y2 = np.cos(x)
plt.plot(x, y1, label="sin")
plt.plot(x, y2, linestyle="--", label="cos")
plt.xlabel("x")
plt.ylabel("y")
plt.title("sin & cos")
plt.legend()
plt.show()
これを表示すると以下のようなグラフが表示されます。

こんな感じで様々なグラフを描画することができます。とても便利ですね。
