概要
Shadertoyのこの作品を見ていたら知った手法。
通常の2Dテクスチャを3Dモデルの位置と法線から投影するように貼り付ける方法です。
詳細については以下の記事をご覧ください。
今回はこれを理解するために自分なりのメモとして書きました。
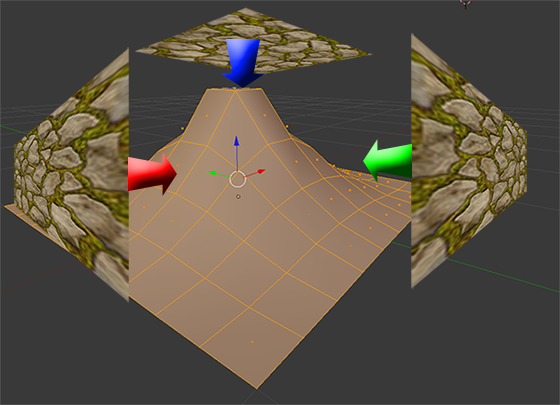
実行すると以下のように、通常の2Dテクスチャを立体的に貼り付けることができます。
(ちなみに下の例はレイマーチによって描き出されたCubeに対して、2Dのテクスチャを貼り付けているところです)

解説
冒頭でも書いたようにこちらのShadertoyの作品で使用されているものを参考にしました。
言及されている記事のURLがすでになくなっていたので検索して見つけた以下の記事を参考に実装しています。
まずはコードを。
vec3 tex3D(sampler2D tex, vec3 p, vec3 n)
{
vec3 blending = abs(n);
blending = normalize(max(blending, 0.00001));
// normalized total value to 1.0
float b = (blending.x + blending.y + blending.z);
blending /= b;
vec4 xaxis = texture(tex, p.yz);
vec4 yaxis = texture(tex, p.xz);
vec4 zaxis = texture(tex, p.xy);
// blend the results of the 3 planar projections.
return (xaxis * blending.x + yaxis * blending.y + zaxis * blending.z).rgb;
}
コード自体は長くないですね。
なにをやっているかのイメージは、参考にさせてもらった記事から引用すると以下のようになります。
※ 対象位置に対して3方から2Dテクスチャをプロジェクションしているようなイメージです。
では順を追って見ていきましょう。
法線を調整
まず冒頭で行っている部分ですが、(おそらく)法線を使える形に調整しているものと思われます。
該当コードは以下。
vec3 blending = abs(n);
blending = normalize(max(blending, 0.00001));
nが法線です。これをabsすることによってマイナスをなくします。(テクスチャの値調整に利用するのでマイナスはいらないってことですね)
そして次の行のmaxですが、これはゼロベクトルによる処理をなくすためかなと。
0.00001とのmaxを取ることでゼロの値を少しだけ底上げしています。
そしてさらにそれをnormalizeで正規化します。
合計値を1.0になるように調整
さて次の部分は何をしているかというと、(利用箇所を見ると分かりますが)法線の値の合計を1.0になるように調整しています。
float b = (blending.x + blending.y + blending.z);
blending /= b;
上で調整したベクトルをさらにその合計で割っています。
つまり、調整されたあとのベクトルはxyz成分の合計が必ず1.0になる、ということです。
例えば、xyzの値が(0.25, 0.43, 0.86)という単位ベクトルがあったとして、今のままだと合計すると1.54になり1.0を超えてしまいます。(あくまでベクトルの長さが1.0の成分のため)
なので、xyz成分すべてをこの1.54で割ることで合計が1.0になるように調整している、というわけですね。
次のところで利用しますが、このベクトルを用いて3方のテクスチャを合成するため1.0を超えないように調整している、というわけですね。
3軸分のテクセルを合成する
最後の部分はテクセルの合成です。
vec4 xaxis = texture(tex, p.yz);
vec4 yaxis = texture(tex, p.xz);
vec4 zaxis = texture(tex, p.xy);
// blend the results of the 3 planar projections.
return (xaxis * blending.x + yaxis * blending.y + zaxis * blending.z).rgb;
最初の部分に注目すると、変数名が軸の名前になっているのが分かるかと思います。
そしてその変数には、評価している点(p)の軸に投影した位置を利用してテクセルフェッチした値が入っています。
例えばxaxisに着目すると、テクセルはp.yzを利用してフェッチしています。(xを無視しているのが分かりますね)
これはx軸を無視したyzの値です。(p.x = 0;とした、と考えてもいいと思います)
要はYZ平面上でのテクスチャの位置をサンプリングしようとしている、というわけです。
それ以外の軸に対するテクセルフェッチも同様の考え方です。
これで3方(3平面)のテクセルを取得することができました。
取得したテクセルを合成する
最後の工程は前述の3方(3平面)のテクセルを適切に合成することです。
以下の部分ですね。
// blend the results of the 3 planar projections.
return (xaxis * blending.x + yaxis * blending.y + zaxis * blending.z).rgb;
合計値を1.0に調整すると書いたのがここの計算の目的のためです。
3つのテクセルを合成するため、合計値が1.0にならないと適切に合成できませんよね。
そのために合計が1.0になるように調整されていたわけです。
そして計算自体はとてもシンプルです。
blendingベクトルは、法線がどの平面に、より向いているかを示すものです。
つまり仮に、真上を向いている法線の場合はyaxisのテクセルを100%採用する、というわけですね。
しかしながら、だいたいの場合において法線は色々な方向を向いているので、そのxyzの値を、どの平面に向いているかの割合と考えて、それを元にテクセルを合成している、というわけなのですね。
ちなみに、xyz = (1, 0, 0)、(0, 1, 0)、(0, 0, 1)と法線を無視してそれぞれの平面に対するテクセルを強制的にフェッチしてみると以下のような結果になります。なんとなくイメージが湧くのではないでしょうか。
まとめ
意外とシンプルなコードながら、Shadertoyで絵を書いていくのに使えるテクニックだなーと思っています。
それに、実際のコンテンツ制作時にも意外と役に立つかもしれませんね。


