概要
ずっと気になっていたIFSとPolar Mod(別の呼び方としてfoldRotateとも)を、@kaneta1992さんが詳しく解説してくれていたので色々Shadertoyでいじってみつつ、コメントを追加してまとめてみます。
以下の記事は必読レベルのいいまとめです!
IFS
IFSはIterated function systemの略で、一言で言うと「ループによって自身の拡縮したり回転したコピーを複製するフラクタル生成システム」ということができると思います。
Wikipediaから引用すると以下のように説明されています。
反復関数系(はんぷくかんすうけい、英: Iterated function system、IFS)はフラクタルの一種であり、一般に2次元のフラクタルの描画や計算に用いられる。IFSフラクタルは自身のいくつかのコピーの和集合から成り、各コピーは関数によって変形されている(そのため「関数系」と呼ばれる)。典型例としてはシェルピンスキーのギャスケットがある。その関数は一般に収縮写像であり、点の集合がより近くなり、形がより小さくなる。従ってIFSフラクタルは、自身の縮小コピーを(場合によっては重ね合わせて)まとめたものであり、各部を詳細に見れば、その部分もそれ自身の縮小コピーから構成されていて、これが永遠に続く。このため、フラクタルとしての自己相似性が生じる。
3次元で言うと「メンガーのスポンジ」が有名かな?
IFSはループによって作られる
IFSを適用して絵を出すのには、ループによってレイを少しずつ変化させながら絵を描いていきます。
(ちなみにレイマーチ自体もループによって作られますが、ここで言うループは意味的にはひとつの距離関数がループによってフラクタル的な構造を取るという意味です)
まずはコードを見てください。
map関数内で行っているのがIFSの処理です。
mat2 rot(float a)
{
float s = sin(a), c = cos(a);
return mat2(c, s, -s, c);
}
float sdBox(vec3 p, vec3 b)
{
return length(max(abs(p) - b, 0.0));
}
float map(vec3 p)
{
vec3 z = p;
float scale = 2.0;
float sum = scale;
float d = 1e5;
for (float i = 0.; i < 4; i++)
{
float td = sdBox(z, vec3(0.5)) / sum;
z = abs(z) - vec3(0, 2.0, 0);
d = min(td, d);
z.xy *= rot(pi * 0.25);
z *= scale;
sum *= scale;
}
return d;
}
よく見ると再帰的な構造になっているのが分かるかと思います。
Cubeの上に45度回転した半分のサイズCubeの上に45度回転した半分のサイズの上に45度回転した・・・というように。
(ちなみに「上」が45度回転した状態になっている点に注意)
今回はループ回数が4回だったので上記のような絵になっていますが、ループ回数を増やすとどんどん小さいCubeが積み重なっていきます。
ループごとに変化を与える
今回の例ではスケールと平行移動、そして回転すべてをループのたびに変化させています。
平行移動
平行移動させている箇所は以下の部分です。
z = abs(z) - vec3(0, 1.0, 0);
absのあとのベクトルを引いている箇所がそれですね。
回転
次に回転です。
回転を適用しているのは以下の部分です。
z.xy *= rot(pi * 0.25);
今回は分かりやすいようにxy平面に限定して回転させています。
当然この箇所を複雑に回転させることでさらに面白い形状にすることも可能です。
スケール
次にスケールです。
z *= scale;
sum *= scale;
スケールはループのたびにzの値を、指定したスケール分乗算していくことで達成しています。
つまりループの回数分どんどんスケールが小さく(or 大きく)なっていく、というわけですね。
そして同時に、sumという変数にもループのたびにscaleを掛けています。
スケールに応じて「距離」を正規化する必要がある
平行移動と回転だけなら特に問題にならないのですが、スケールを扱う際には少し考慮することがあります。
スケールを扱う場合はレイの進む距離に変化が生じてしまうので対策しないとなりません。
@kaneta1992 先生のIFSの解説を見て、「なるほどなるほど。IFS完全に理解した」と思いながらスケールを掛けてみたらうまく動かなかったので、やっぱり実際に手を動かさないとダメですね![]()
ポイントはループごとに掛けられていくスケールの合計で(例では変数sum)、距離関数の値を正規化しているところです。
float td = sdBox(z, vec3(0.5)) / sum;
距離関数で得られた値を**sumで除算**することで正規化しています。
これは、ループのたびにレイがスケールされていくため、前回のループで計算された距離関数の距離とは大きく異なった値が返ってきてしまうためです。
なので距離関数自体を現在のスケール率に合わせて正規化する必要がある、というわけなんですね。
ちなみにこれは@kaneta先生にTwitterで教えていただきました!
ifsの最中でscaleを欠けていくと、どんどん距離場のスケールが大きくなって、最短距離からかけ離れていきます。
— かねた (@kanetaaaaa) June 23, 2019
イテレーションごとに距離を正規化させてやることできれいに表示されます!
Polar Mod
さて次はPolar Mod(またはRotateFold)について。
Polar Modとは、レイマーチングでよく利用されるmodを利用したリピートと考え方自体は同様のものです。
ただ、リピートの仕方がxyz軸に対して繰り返しが表現されるmodに対して、極座標的な感じで繰り返しを行う点が異なります。
ちなみに通常のrepeatに関しては以下のような計算を行うものです。
float map(vec p)
{
p = mod(p, 3.0) - 1.5;
}
これはmap関数に渡ってきたレイの位置(p)に対してmodを適用し、繰り返しが現れるようにしています。
余談
ちなみにShadertoyでこれを関数化して定義していたら、こうしたほうが便利だよ! って教えてもらったのでついでに記載しておきます。
# define repeat(p, span) mod(p, span) - (0.5 * span)
#defineにする理由は、任意の平面(例えばXZ平面とか)に限定して繰り返しさせたい場合に、関数で定義してしまうとvec2やvec3を引数に取るそれぞれの関数を定義しないとなりませんが、#defineなら事前にプリプロセッサによって置換されるためそうした細かい配慮が必要ない、というわけです。
例えば、以下のように異なる要素数の処理についてもひとつの#defineのみで対応できます。
// ひとつの#defineだけで以下に対応できる
p.x = repeat(p.x, 3.0);
p.xz = repeat(p.xz, 3.0);
p.xyz = repeat(p.xyz, 3.0);
便利ですね。
Polar Mod詳細
閑話休題。
さて、ではPolar Modの詳細について。
といってもこちらは@kaneta1992先生の記事を読んだほうが分かりやすいと思うので、あくまでも自分の理解のためのメモです。
// Rotate matrix for 2 dimension
mat2 rot(float a)
{
float c = cos(a), s =sin(a);
return mat2(c, s, -s, c);
}
// r is splited number.
vec2 pmod(vec2 p, float r)
{
float a = atan(p.x, p.y) + pi / r;
// "+ pi / r" means shortcut of "+ ((pi2 / r) * 0.5)".
// so we want to get half angles of circle splitted by r.
float n = pi2 / r;
a = floor(a / n) * n;
// floor(a / n) means calculating ID.
return p * rot(-a);
}
// map function. This will render the scene.
float map(vec3 p)
{
p.xy = pmod(p.xy, 5.);
vec3 offs = vec3(0, 2, 0);
return length(p - offs) - 1.0;
}
処理自体はとても短いですね。そしてメインとなる関数は当然pmod関数です。
関数解説
それぞれの関数を見ていきましょう。
回転行列を返す関数rot
最初は回転行列を返す関数rotです。
これ自体は取り立てて特別なところはありません。
2次元での回転を想定している、という点だけ注意が必要です。
mat2 rot(float a)
{
float c = cos(a), s =sin(a);
return mat2(c, s, -s, c);
}
普通の2次元の回転行列を生成しています。
3次元的な回転でももしかしたらいいのかもしれないですが、今回のPolar Modは「いずれかの面」を回転させて分割する方法です。
特に今回の例ではxy平面に対して回転を施しています。
平面を回転することを前提にしているため、2次元での回転行列を計算しているわけなんですね。
実際に利用されている部分を見てみると以下のようになっています。
// xy平面の「2次元」だけに適用している
p.xy = pmod(p.xy, 5.0);
Polar Mod本体
次に見るのはPolar Mod自体の関数です。
以下の部分ですね。
vec2 pmod(vec2 p, float r)
{
float a = atan(p.x, p.y) + pi / r;
// "+ pi / r" means shortcut of "+ ((pi2 / r) * 0.5)".
// so we want to get half angles of circle splitted by r.
float n = pi2 / r;
a = floor(a / n) * n;
// floor(a / n) means calculating ID.
return p * rot(-a);
}
重要なポイントを雑に書くと、
- 360度を分割数で割りイチ区画分の角度を求め、その角度の範囲内で繰り返しになるようにレイの位置を回転させる
- 角度の計算時にイチ区画分の角度の半分だけオフセットさせる
です。
ちなみにオフセットを加える理由ですが、@kaneta1992さんの記事から引用させてもらうと以下のように説明されています。
オフセットを加えていない場合、空間の切れ目が画面中央に存在していますよね?
空間の切れ目にオブジェクトが移動してしまうので、見切れた形で複製されてしまいます。
余談
少し横道にそれますが、これは通常のmodを利用したリピートでも同様の問題があり、補正する理由もだいたい同じなのでここで解説しておきます。
簡単な例を示すと、UVの値に対してmodを適用してみると以下のような繰り返しになります。
計算式としては以下です。
void mainImage(out vec4 fragColor, in vec2 fragCoord)
{
vec2 uv = (fragCoord * 2.0 - iResolution.xy) / iResolution.xy;
uv = mod(uv, 1.0);
vec3 col = vec3(uv, 0);
fragColor = vec4(col, 1.0);
}
図で見ると分かるように、左右対称ではなく中央からばっつりと分かれている絵になっているのが分かるかと思います。
これはfloorの仕様として引数の値以下の最大の整数を返すのが理由です。
プラス方向の場合はfloor(0.5) == 0、floor(1.2) == 1となりますが、マイナス方向の場合はfloor(-0.1) == -1となります。
与えられた引数以下の整数なので、-0.1より小さい-1になる、というわけですね。
そしてGLSLのmodのドキュメントには以下のように書かれています。
mod returns the value of x modulo y. This is computed as x - y * floor(x/y).
これを使って計算すると、xが-0.1のとき(つまり上の例の図で言うと、画面中央からやや左に移動したあたり)は、
// x = 0.1, y = 1.0の場合
float newX = -0.1 - 1.0 * floor(-0.1 / 1.0); // -0.1 * 1.0 * -1.0
// newX = 0.9
となり、まさに上の図のような配色なるというわけです。
画面中央すぐ左あたりを注目してもらうと(-0.1とか)は0.9となってしまっています。(赤目の色になっている=xの値が1.0に近い)
つまり空間的には右端となってしまいます。そのため、レイの位置が突然右端に移動してしまうのでオフセットを与えてあげないときれいな繰り返しにならない、というわけなんですね。
そしてオフセットをする理由を図にすると以下のようなイメージ。
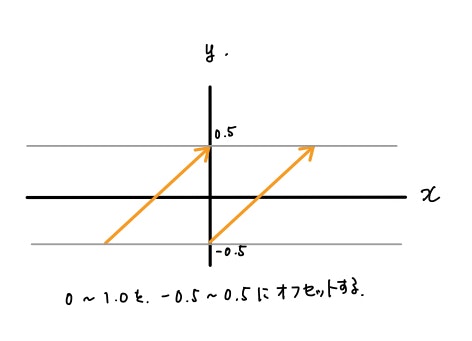
上の図は、yの値だけmodによって繰り返している様子を示しています。
なので矢印の高さが常に同じところを繰り返しているのが分かるかと思います。
そして大事な点は、一律-0.5を加えてyの値をオフセットさせている点です。
こうすることで、0 ~ 1の間になってしまっていたものを-0.5 ~ 0.5という範囲に変換している、というわけなんですね。
なのでオフセットを繰り返し単位の半分だけ与えればきれいに中心が空間の真ん中にオフセットされる、というわけです。
回転角度の計算
閑話休題。
話を戻しましょう。
Polar Modの関数の最後から見てみると、最終的にreturn p * rot(-a);として元のレイの位置をなにがしかの角度分回転させた位置を返しています。
なのでこのaの算出方法を理解すればPolar Modを理解することができるはずです。
では問題のaの算出方法を見てみましょう。
float a = atan(p.x, p.y) + pi / r;
float n = pi2 / r;
a = floor(a / n) * n;
計算自体はそこまで複雑なことを行っていません。
まず最初に行っているのは、引数に渡ってきたpの位置(2次元であることに注意)を、atan関数を使ってそのベクトルの角度を求めます。
ちなみにatan関数のドキュメントにはこう記載されています。
atan — return the arc-tangent of the parameters
genType atan(genType y,
genType x);
つまりアークタンジェントのatanですね。
そして返ってくる値はラジアンです。
そしてその返ってきた角度に対して、さらに**180度(=pi)**を分割数で割った数値を足しています。
これは通常のModによるリピートと同様に、レイの位置を補正するためのオフセット処理です。
ちなみに通常のmodでは分割数の半分だけオフセットさせると書きましたが、今回は半分ではない? と思った方。
上書いた最初のコードではコメントしてますが、計算自体に半分を示す値はありませんが、そもそも360度を分割数の半分で、と考えると、piはすでに360度の半分なので、半分にする処理がいらないわけですね。
そして次のnの計算は空間的なインデックスの計算です。
次の行でfloor(a / n) * n;と、floor関数を利用しているのがその特徴です。
floor関数は小数点部分を切り捨て、整数部分だけを返してくれる関数です。
これをグラフにしてみると以下のようになります。
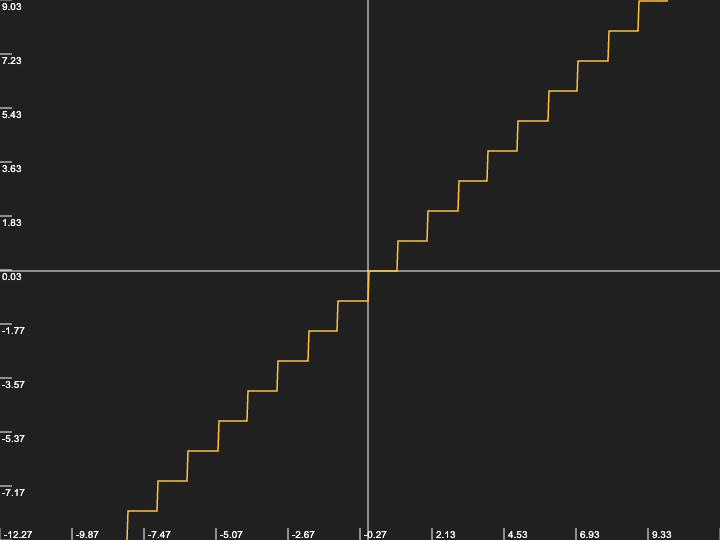
このように、整数部分だけを取り出すことで、その範囲のインデックスとして利用できるわけなんですね。
(なので、作品によってはidっていう変数名が付けられていたりも)
そしてその値と、さらにnを掛けることで値を正規化しているというわけです。
あとはこの値分だけ回転させれば無事、Polar Modの完成です。
詳細については@kaneta1992先生の記事を御覧ください。こちらでは図解もされているので分かりやすいと思います。
最後に
最後に。
IFSとPolarModを使って作ってみたのがこちら↓

IFSとPolerModを使うだけでだいぶ複雑な絵になるのが分かるかと思います。
これを色々応用すれば、比較的シンプルなシーンをいっきにリッチな見た目にできるので楽しいですね。