ドロネー三角形をWikipediaから引用します。
ドロネー図（ドロネーず、英語：Delaunay diagram）あるいはドロネー三角形分割（ドロネーさんかっけいぶんかつ、триангуляция Делоне, Delaunay triangulation）は、距離空間内に離散的に分布した点の集合に対し得られる、それらをある方法に従い辺で結んだ図形である。
プログラムからドロネー三角形分割が作れるメリットとしては、適当に散らばった点をいい感じに三角形に分割してくれる＝三角形ポリゴンとして利用できるようになる、というのが大きなところでしょう。
それ以外でも、点の集合をすべて内包する凸包を検出したり、といったこともできるようになります。
なので、アルゴリズムを知って使えるようになっておくのはそれなりにメリットがあると思うので、調べつつ、自前で実装できるところまで挑戦してみました。
実際に挑戦した結果
今回挑戦した内容を、jsdo.itに上げてあります。
また、作成したものをGithubにも上げておきました。
今回の実装のアルゴリズムは、以下の記事を参考にさせてもらいました。
全体的なアルゴリズムは最初の記事をベースに、再分割に関してはProcessingでDelaunay分割（解説篇）をヒントに実装しました。
アルゴリズムの概要
ちなみにアルゴリズムはいくつもあるようです。
その中でも比較的簡単なものがよく紹介されているので概要を紹介しておきます。
- とある点の集合すべてを含むような巨大な三角形を追加する
- 点集合のうち、i番目の点（Pi）を三角形分割図形に追加（初期であれば、巨大三角形の中に集合の中のどれかの点を入れるところから開始）
- 点Piを含む三角形ABCを見つけ (※1)、点Piを使ってその三角形を分割する（ABPi,BCPi, CAPiの3つの三角形） このとき、辺AB, BC, CAをスタックに積む（仮にスタックをSとする）
- スタックSが空になるまで以下を繰り返す (※2)
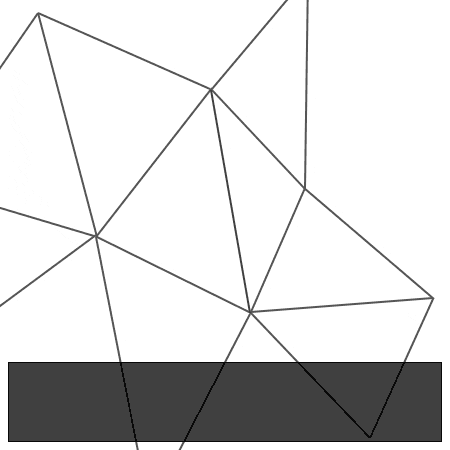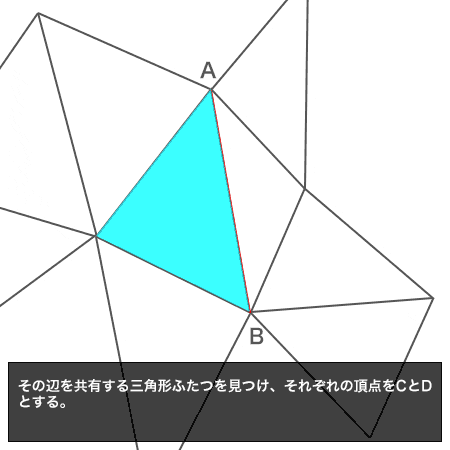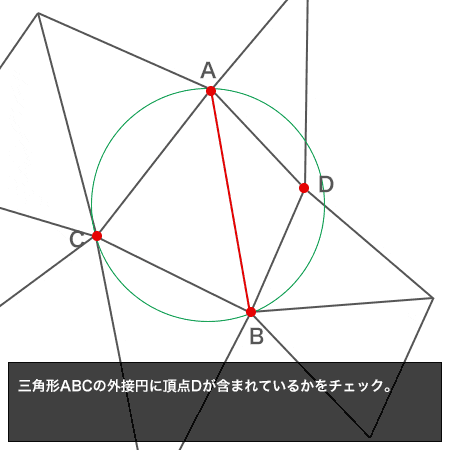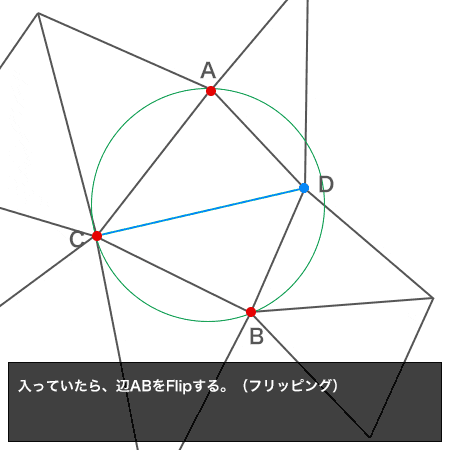
- スタックSの一番上のedgeをpopする。これを辺ABとする
- 辺ABを含む2個の三角形をABC, ABDとする 三角形ABCの外接円にDが含まれる場合は、辺ABをフリップし、辺AD/DB/BC/CAをスタックSにpushする そうでないなら処理をスキップする
- super triangleとそれに関する頂点を破棄する（巨大三角形は処理をシンプルにするための架空のものなのでそれを消去する）
※1 ... 点Piを含む三角形の判定は、 外接円に含まれるか という判定な点に注意。
※2 ... Flip（フリッピング） が具体的にどういうことか最初文章からだと分かりづらかったので、それをアニメーションgifにしてみました。
実装メモ
アルゴリズムが分かったところで、それをプログラムに落としていかないとなりません。
今回の実装の中で、いくつかのポイントがあるのでそれをまとめます。
すべての点を含む巨大三角形を作る
今回は、参考にした記事と同様に画面サイズ内にドロネー三角形分割を生成する前提で実装しました。
実装自体は、点集合すべてを内包する四角形を決め、それの外部三角形を得ることで対応しています。
この「内包する四角形」を、それぞれ必要に応じて変えることで、任意の範囲のドロネー三角形分割を行うことができるはずです。（巨大三角形を得る計算は任意の四角形から得る実装になっている）
外接円を得る
ドロネー三角形分割を行う上で、外接円が大事なポイントになります。その外接円を計算する方法です。
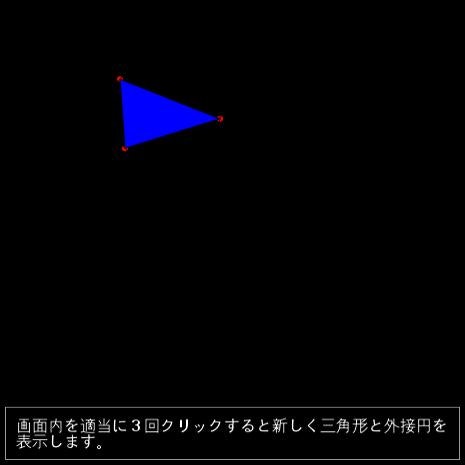
外接円を得る簡単なデモをjsdo.itに上げました。
画面内を適当に3回クリックすると三角形が描かれ、それに対して外接円が表示されます。
アルゴリズムの詳細についてはこちらの記事を参考にしてください。
仕組み自体はシンプルです。
簡単に説明すると、外接円の特性として「三角形の全頂点と円の中心は、半径の長さに等しい」のでそれを計算で算出します。
概要を書くと、以下の方程式を解くことになります。
※x, yは外接円の中心座標とします。
(x_1 - x)^2 + (y_1 - y)^2 = (x_2 - x)^2 + (y_2 - y)^2 = (x_3 - x)^2 + (y_3 - y)^2
この式は「ピタゴラスの定理」の以下を利用したものです。（Wikipediaからの引用）
平面幾何学において直角三角形の斜辺の長さを c、他の2辺の長さを a, b とすると、
a2 + b2 = c2
これを中心座標(x, y)について解くと、
x = \frac{ (y_3 - y_1)(x_2^2 - x_1^2 + y_2^2 - y_1^2) + (y_1 - y_2)(x_3^2 - x_1^2 + y_3^2 - y_1^2) }{c}
y = \frac{ (x_1 - x_3)(x_2^2 - x_1^2 + y_2^2 - y_1^2) + (x_2 - x_1)(x_3^2 - x_1^2 + y_3^2 - y_1^2) }{c}
となり、中心座標が得られる。ただし
c = 2 ( (x_2 - x_1)(y_3 - y_1) - (y_2 - y_1)(x_3 - x_1) )
である。
データクラス
主なロジック部分は、実はそれほど多くありません。
上記の部分が作れてしまえば、あとはわりと地道な作業です。
今回の実装のために準備したデータクラス郡は以下の通り。
| クラス | 説明 |
|---|---|
| Point | 任意の点（座標）を表すクラス |
| Size | サイズを表すクラス |
| Edge | 辺を表すクラス。始点と終点のふたつのPointクラスを保持する |
| Triangle | 三角形クラス。3つの頂点としてのPointクラスと、3辺のEdgeクラスを保持する |
| Rectangle | 四角形クラス。外部三角形を得るために利用 |
| Circle | 円クラス。外接円を表すために利用 |
各クラスには同値判定や、該当の点や辺を含んでいるかのチェック用メソッドが定義されています。
が、どれも単純に総当りでチェックしているだけなのでロジック的にはとてもシンプルです。
あとは、それらを使いながら、最初に示したアルゴリズムを適宜実行していく、という感じでした。
サンプルのソースにはなるべく多くのコメントを入れているので、興味がある人は見てみてください。