概要
最近では主流になっている「物理ベースレンダリング」の概要をまとめたいと思います。
物理ベース、と呼ばれることから分かるように、レンダリングする際の色の決定を物理ベース、つまり「光のエネルギーを用いて」表現することを言います。
エネルギーを用いて表現することにより、実際にそこにどれくらいの光が集まっているのか、という点からレンダリングするために、実際の映像のように写実的な表現が可能となります。
(とはいえ、いくつもの近似を重ねているのでやっぱりまだどこか映像感があるのも否めませんが)
レンダリング方程式
レンダリング方程式は「エネルギー保存の法則」を基礎に、ある程度光学的に正しい光の状態の近似として方程式を解くものです。
物理ベースレンダリングを勉強しているといくつかの方程式が出てきますが、高速に解く方法だったり、より最適な近似を行うものだったり、といった違いがあります。
ただ基本的にはこの「レンダリング方程式」を解くための道具として登場することがほとんどだと思います。
以下の方程式は「ゲームアプリの数学 Unityで学ぶ基礎からシェーダーまで」に記載されているものです。
(ここでまとめている内容は上記書籍をベースに、いくつかの記事を参考に書いています)
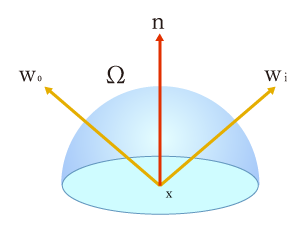
L_0(x, \vec{w_0}) = L_e(x, \vec{w_0}) + \int_\Omega f_r(x, \vec{w_i}, \vec{w_0}) L_i(x, \vec{w_i})(\vec{w_i} \cdot \vec{n}) d\vec{w_i}
ざっくり方程式の意味を説明すると、地点 $x$ (要はレンダリングしようとしているピクセル)についての光の放射がどの程度起こるか、を示しています。
(結局のところ、人の目に色として認識されるのは、該当の物体が光を反射し、それを目で捉えているからなわけで、それをシミュレートしている、というわけですね)
また上記方程式にはベクトルが多数出てきますが、これは目に入る光の量は向きに依存するため、方向を示すベクトルが重要な意味を持つわけです。
解説
上記の数式の意味を、それぞれの項ごとに書いていきたいと思います。
L_0(x, w_0)
これは**放射輝度(radiance)**と呼ばれ、地点 $x$ から $w_0$ 方向に放射される光のエネルギーの総量($\Omega$)です。
まぁ要は光がどれくらい出てくるのか=どんな色か、ってことですね。
$w_0$ は視線方向へのベクトル、$w_i$ は入射する光の逆ベクトル、$n$ は面の法線、$x$ はレンダリングしようとしている点、$\Omega$ は半球の総和を示す記号です。
L_e(x, w_0)
これは物体そのものが光っている場合などに光の総量に加算される項となります。
例えば電球だったり、炎の光だったりですね。
なので基本的には自身が光っているオブジェクトはそう多くないので、ほとんどの場合でここは $0$ になると思います。
\int_\Omega f_r(x, w_i, w_0) L_i(x, w_i)(w_i \cdot n) dw_i
インテグラル($\int$)がありますが、これは地点 $x$ に入射する光をすべて足し合わせたもの、という解釈でいいと思います。(なので積分)
上の図で言うと、グラデーションになっている半球上に入射する光の総量($\Omega$)となります。
つまり、地点 $x$ に集まる光をすべて足し合わせ、かつそこから放射される光エネルギーの総量を解く方程式がレンダリング方程式だ、ということですね。
なのでこの方程式を解くと、結果として物質からの光の強さ(=色)が求まるというわけです。
L_i(x, w_i)
上記は間接光を含む、すべての入射する光を表します。
(w_i \cdot n)
これは、面法線 $n$ と入射光とが成す角による、光の減衰を表しています。
この内積は、面法線と入射光とのコサイン項にあたり、ラディアンスが「単位射影面積あたり」の放射束と定義されているため、このような計算が必要となります。
f_r(x, w_i, w_0)
そして上記は BRDF と呼ばれる、$w_i$ からの入射光のエネルギーとしての放射照度(irradiance)と、$w_0$ への反射光のエネルギー量としての放射輝度の比率を表す関数です。
BRDF
BRDFは色々なところで出てくるのでもう少しだけ丁寧に。
物理ベースのレンダリングについて学んでいると出てくる BRDF 。
略は Bidirectional Reflectance Distribution Function (双方向反射率分布関数) です。
ざっくり言えば、面に対して光がどう反射するのかをモデル化したものです。
なので3Dをある程度やったことがある人であればお馴染みの「ランバート反射」や「フォン反射」を、より一般化した関数である、とも言えます。
図にすると以下のようになります。入射する光がどう反射するのかを図解したものです。
(緑色のエリアは一定方向にだけ反射するのではなく、ある範囲(線ではなく面)の方向に拡散反射している様子を表しています)

ちなみに、BRDFは以下のふたつの物理法則を満たすように定義されます。
- エネルギー保存の法則 ... 入射光以上の強さの反射光は出てこない
- 相反性 ... 入射と反射を逆転させても値が変化しない(ヘルムホルツの相反性)
この制約により、物理法則から外れた計算結果が得られる、ということを防いでいます。
上記でも触れたように、方程式はいくつも考案されていてそのどれもが同じことを別のアプローチで実現しているものになります。
その中でも、有名な(おそらく。いろんな記事見ていると最初に紹介されてるケースが多い)クックトランスのモデルを紹介します。
クック-トランスモデル
ちなみに参考にした書籍でも紹介されており、書籍によれば、オーレン-ネイヤーの拡散反射モデルなど複数あるものの、リアルタイムレンダリングではそこまで大きな差は出ないとのこと。
(要は、クック-トランスモデルで十分ということ? ただ、おそらくこれの亜種やら様々なモデルがありそう)
クック-トランスモデルの基本形
f(L, V) = \frac{D(H)F(V, H)G(L, V, H)}{4(N \cdot L)(N \cdot V)}
ここで $L$ は入射光ベクトル、$V$ は視線ベクトル、$H$ は $L$ と $V$ のハーフベクトルです。
クック-トランスモデルはいくつかの項を計算します。
それぞれが関数になっており、関数は以下です。
$D$
法線分布関数(normal distribution function, NDF)
$D$は主に、シェーディング時のハイライトの形状として現れるもののようです。
ちなみにここでの「法線」はマイクロファセット(*)に対する法線を指します。
こちらの記事の説明が分かりやすいので引用させていただくと、
- D(m) はマイクロファセットの分布関数です. 例えばハーフベクトル h を代入した場合には, D(h) はスペキュラを跳ね返すことができるハーフベクトル h と一致する法線を持つマイクロファセットの分布の値を取得していることになります.
- D(m) の値が取り得る範囲は 0 ~無限大で, 単位系は 1/sr です.
- しかし, D(m) は下図のようにマイクロファセットを射影した面積の球積分の和が 1 になる必要があります. (法線の保存則っぽい感じ)
※ 画像に関しては上記記事を参考にしてください。
$F$
フレネル項。いわゆるフレネル反射の項ですね。
ざっくり言うと、水面に対する視線ベクトルの角度によって反射率・透過率が異なるものをモデル化したもの、です。(多分・・)
この記事がとても分かりやすいと思います。
(その7 斜めから見ると底が見えない水面(フレネル反射))
さらに、こちらの記事から説明を引用させてもらうと、
- 空気から他の物質に入射しようとした光は, その表面を跳ね返る光(反射する光)とその表面の中に進入する光(屈折する光)の 2 つに分かれます.
- つまり, "入ろうとした光" = "反射した光" + "屈折した光" というように, 2 つに分かれることになります.
- この "入ろうとした光" を100 % としてそれが面に対して入射の角度 10 °で入ろうとした結果, "反射する光" の割合が 90% で 屈折する光が 10% になったとします.
- この場合, フレネル反射率 F(10°) = 0.9 となります.
- フレネル反射率は "物質ごとの屈折率" と "光が物質に対して入る角度" の 2 つによって決まります.
ちなみに物質ごとの反射率は物質ごとに決まっているようです。
特に、物質に対して垂直な視線に対する反射率などは $F(0°)$ などと書いて計算に利用されます。
$G$
幾何減衰(geometric attenuatin)。
マイクロファセットの凹凸が、視線、入射光、反射光ベクトルを途中で遮ることによって生じる影響を表す項です。
※マイクロファセット
マイクロファセットとは、マイクロなファセットの集まりを意味します。
(ファセットの単語の意味を調べると「(結晶体・宝石の)小面、(カットグラスの)切り子面、(物事の)面、相」と書いてあります。参照: weblio)
つまり、ランバート反射では物質のもつこうした微細面に対して考慮せず、一律に計算していたものを、分布関数として計算し、より精密な反射の近似として用いる概念、ということができると思います。
図にすると以下のように、複雑な微小面に対しての法線の分布を求める関数となります。
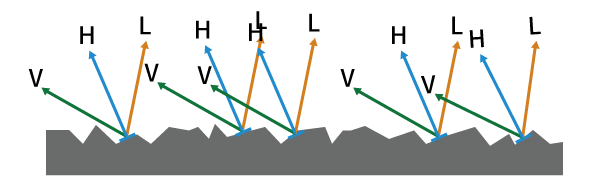
※ $V$ は視線ベクトル、$L$ は入射する光の逆ベクトル(つまり光源への方向)、$H$ はそれらのハーフベクトルです。
実装
GGX(Trowbridge-Reitz)
前述のように、クック-トランスモデルで用いられている関数にもいくつも種類があり、今回は「GGX」のモデルを利用しています。
GGXでは $α = (roughness)^2$ のときに以下の方程式となります。
D_{ggx}(H) = \frac{α^2}{\pi((N \cdot H)^2 (α^2 - 1) + 1)^2}
フレネル項
F_{Schlick}(V, H) = F_0 + (1 - F_0)(1 - V \cdot H)^5
ちなみにここでの $V \cdot H$ は $cos \theta$ を求めるための計算です。
幾何減衰
G_{Cook-Torrance}(L, V, H) = min(1, \frac{2(N \cdot H)(N \cdot V)}{V \cdot H}, \frac{2(N \cdot H)(N \cdot L)}{V \cdot H})
コード断片
Properties {
_Color ("Diffuse Color", Color) = (1,1,1,1)
_Roughness ("Roughness", Float) = 0.5
_FresnelReflectance ("Fresnel Reflectance", Float) = 0.5
}
まずは必要な項目をプロパティとして宣言します。
struct appdata {
float4 vertex : POSITION;
float3 normal : NORMAL;
};
struct v2f {
float4 pos : SV_POSITION;
float3 normal : TEXCOORD1;
float4 vpos : TEXCOORD2;
};
頂点シェーダ、フラグメントシェーダで使用する構造体は今回はこんな感じです。
v2f vert(appdata v) {
v2f o;
o.pos = mul(UNITY_MATRIX_MVP, v.vertex);
// ワールド空間での法線を計算
o.normal = normalize(mul(_Object2World, float4(v.normal, 0.0)).xyz);
// 該当ピクセルのライティングに、ワールド空間上での位置を保持しておく
o.vpos = mul(_Object2World, v.vertex);
return o;
}
頂点シェーダではそれぞれ計算に必要なパラメータ、主にワールド空間での法線と頂点位置を計算してフラグメントシェーダに渡します。
float4 frag(v2f i) : COLOR {
// 環境光とマテリアルの色を合算
float3 ambientLight = unity_AmbientEquator.xyz * _Color.rgb;
// ワールド空間上のライト位置と法線との内積を計算
float3 lightDirectionNormal = normalize(_WorldSpaceLightPos0.xyz);
float NdotL = saturate(dot(i.normal, lightDirectionNormal));
// ワールド空間上の視点(カメラ)位置と法線との内積を計算
float3 viewDirectionNormal = normalize((float4(_WorldSpaceCameraPos, 1.0) - i.vpos).xyz);
float NdotV = saturate(dot(i.normal, viewDirectionNormal));
// ライトと視点ベクトルのハーフベクトルを計算
float3 halfVector = normalize(lightDirectionNormal + viewDirectionNormal);
// D_GGXの項
float D = D_GGX(halfVector, i.normal);
// Fの項
float F = Flesnel(viewDirectionNormal, halfVector);
// Gの項
float G = G_CookTorrance(lightDirectionNormal, viewDirectionNormal, halfVector, i.normal);
// スペキュラおよびディフューズを計算
float specularReflection = (D * F * G) / (4.0 * NdotV * NdotL + 0.000001);
float3 diffuseReflection = _LightColor0.xyz * _Color.xyz * NdotL;
// 最後に色を合算して出力
return float4(ambientLight + diffuseReflection + specularReflection, 1.0);
}
フラグメントシェーダで、上記で紹介した方程式を解きつつ、スペキュラとディフューズを計算し、出力としています。
さて、各項の計算は以下のようになります。
// D(GGX)の項
float D_GGX(float3 H, float3 N) {
float NdotH = saturate(dot(H, N));
float roughness = saturate(_Roughness);
float alpha = roughness * roughness;
float alpha2 = alpha * alpha;
float t = ((NdotH * NdotH) * (alpha2 - 1.0) + 1.0);
float PI = 3.1415926535897;
return alpha2 / (PI * t * t);
}
// フレネルの項
float Flesnel(float3 V, float3 H) {
float VdotH = saturate(dot(V, H));
float F0 = saturate(_FresnelReflectance);
float F = pow(1.0 - VdotH, 5.0);
F *= (1.0 - F0);
F += F0;
return F;
}
// G - 幾何減衰の項(クック トランスモデル)
float G_CookTorrance(float3 L, float3 V, float3 H, float3 N) {
float NdotH = saturate(dot(N, H));
float NdotL = saturate(dot(N, L));
float NdotV = saturate(dot(N, V));
float VdotH = saturate(dot(V, H));
float NH2 = 2.0 * NdotH;
float g1 = (NH2 * NdotV) / VdotH;
float g2 = (NH2 * NdotL) / VdotH;
float G = min(1.0, min(g1, g2));
return G;
}
今回のサンプルはGitHubにも上げておいたので、動作するものが見たい場合はそちらを確認ください。