概要
今回は2次元の六角形を描き出す方法の解説です。
これを応用して、レイマーチした平面に描き出すとこんな感じの絵が作れます↓

動くものはShadertoyに上げてあります。
ちなみにこのUV値による描画は以下の動画を大いに参考にさせていただきました。
動画ではひとつひとつ、徐々に作り上げていってくれるのでとても参考になります。
時間がある方は動画を見たほうがより理解を深められるかもしれません。
六角形(Hexagon)を描く
さて、まずは六角形を描く方法を見ていきましょう。
UV値を加工して六角形を描き出します。
まずはコードを示し、そのあとで解説を加えます。
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (fragCoord - 0.5 * iResolution.xy) / iResolution.y;
vec3 col = vec3(0);
uv = abs(uv);
float d = dot(uv, normalize(vec2(1.0, 1.73)));
d = max(d, uv.x);
col = vec3(step(d, 0.2));
fragColor = vec4(col,1.0);
}
最終的にはこれを繰り返し処理して配置することで冒頭の絵にしていきます。
六角形が描ける理由
今回は特に、正六角形を描く場合の話となります。
まずコードを順に説明していきましょう。
UV値を-1 ~ 1の間に正規化するのはよくある方法ですね。
まずは原点を画面中心に持っていくための処理です。
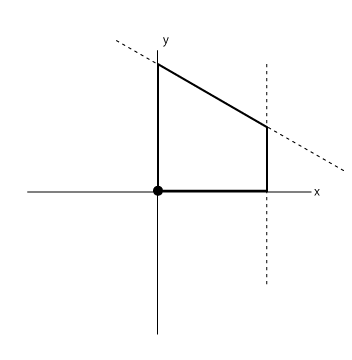
そして今回は特に、uv = abs(uv)とすることで、第一象限だけに絞って考えるというのがポイントになります。
つまり図にすると以下のようなことに限定して考える、ということです。
この部分だけを描くことができれば、あとはabsによって全方位に図が描かれ、結果として上の図のように六角形が描かれる、というわけです。
まずはUVの値を視覚化する
さて今までの状態だけを使ってUV.xの値を視覚化すると以下のようになります。
col = vec3(uv.x);
absによって中央から左右に値が増えていっているのが確認できますね。
これをさらにstep関数によって区分けを行うと以下のようになります。
col = vec3(step(uv.x, 0.2));
※ step関数は本来、第一引数がedgeを表します。しかし上の例では逆に渡している点に注意してください。そのため結果が逆転しています。
ドキュメントによると、
step generates a step function by comparing x to edge.
For element i of the return value, 0.0 is returned if x[i] < edge[i], and 1.0 is returned otherwise.
と書かれており、第二引数(x)が第一引数(edge)以上か以下かで0.0か1.0を返してくれる関数となっています。
それを考慮しつつ結果を見てみると以下のようになります。
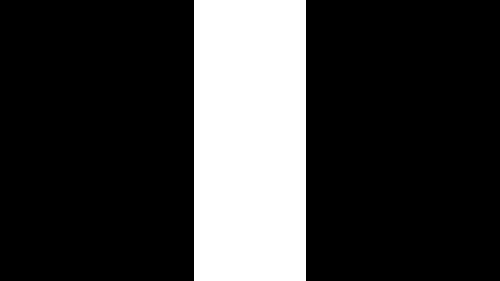
今回の例ではuv.x < 0.2を堺に色が区分けされています。
とあるベクトルとの内積を距離に用いる
では次のコードを見てください。
冒頭で紹介したコードの一片です。
float d = dot(uv, normalize(vec2(1.0, 1.0)));
col = vec3(step(d, 0.2));
vec2(1.0, 1.0)を正規化したベクトルとUVの内積を取り、さらにそれをstep関数で加工しています。
これは一体なにをしているんでしょうか。
これをグラフにすると以下のような図になります。
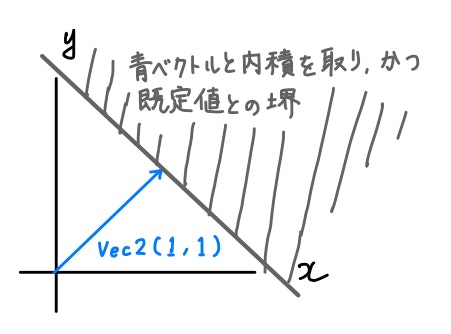
ベクトルとの内積を取るということはすなわち、そのベクトルに対してもう片方のベクトルを射影することを意味します。
そしてstep関数によってしきい値前後で境を作ると、上の図のように境界が現れる、というわけです。
これを視覚化すると以下のようになります。

徐々に形が見えてきましたね。
現状ではvec2(1.0, 1.0)のベクトルに対して内積を取っています。
が、これだと正六角形にはなりません。
角度を考慮する必要があるわけですね。
vec2(1.0, 1.0)によって角度がついたということは、これを適切なベクトルにすることで正六角形の形を作ることができるようになります。
ではどんなベクトルを採用したらいいのでしょうか?
そのベクトルを求めるためには以下の図を見てください。
まず、六角形の中に直角三角形を配置します。
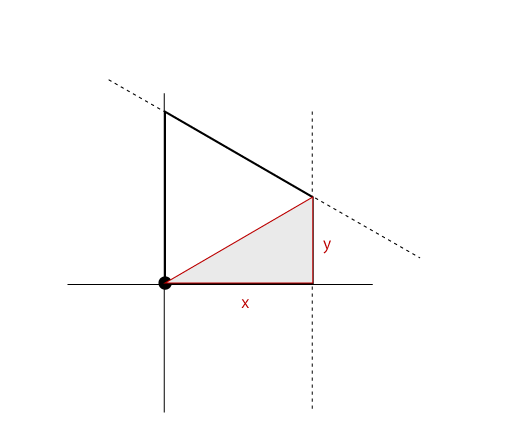
これを以下のように回転させます。すると六角形の斜辺に対して直角となる部分が現れました。
この方向を向くベクトルを求めれば、上で書いたベクトルを求めることができそうです。
ではどう求めればいいのでしょうか。
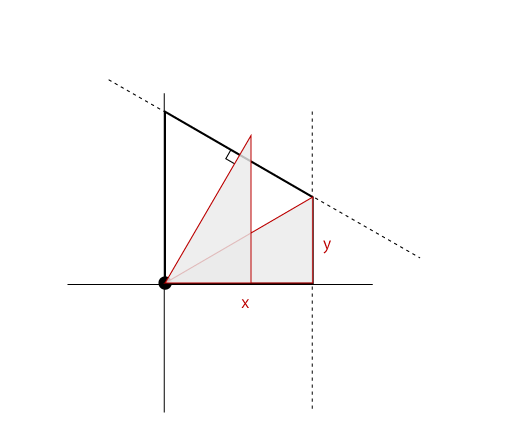
最初の三角形を以下のように拡大します。するとyを1とすると比率的に斜辺は2となることが分かります。
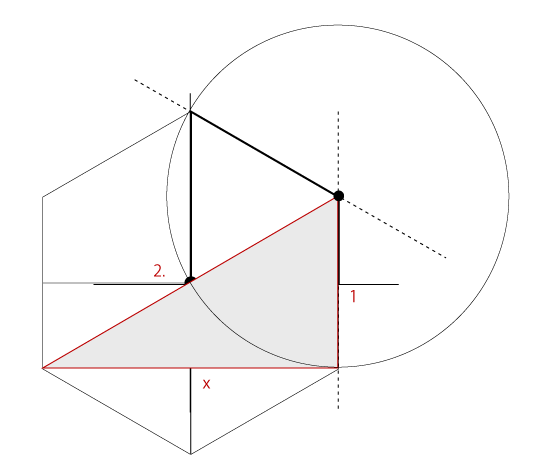
このとき、縦の辺は1、そして底辺をxと置き、斜辺は2となります。
ここから、
\sqrt{x^2 + y^2}^2 = 2^2 \\
x^2 + y^2 = 4 \\
// y = 1なので \\
x^2 + 1^2 = 4 \\
x^2 = 4 - 1 = 3 \\
x = \sqrt{3} \fallingdotseq 1.73
となります。
つまりnormalize(vec2(1.0, 1.73))というベクトルがほしかったベクトル、ということになりますね。
そしてこれを適用して視覚化すると以下のようになります。

あとはこの四角形の角を切り落とすことができれば、念願の六角形が姿を表します。
そしてそれをどうやるかですが、正六角形ということを利用して、左右の辺までの長さをuv.xの値でクリッピングします。
具体的には以下のようにします。
d = max(d, uv.x);
上記のようにuv.xの値を最大値としてクリッピングすると以下のように正六角形が姿を表します。

繰り返しを用いて六角形をタイリングする
さて、次に行うのは六角形をタイリングすることです。
が、実は上記の方法はある程度概念を学ぶのみで、繰り返しの場合は登場しません。
まずは繰り返しを実行したコードを見てみましょう。
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
vec2 uv = (fragCoord - 0.5 * iResolution.xy) / iResolution.y;
uv *= 4.0;
vec3 col = vec3(0);
vec2 r = normalize(vec2(1.0, 1.73));
vec2 h = r * 0.5;
vec2 a = mod(uv, r) - h;
vec2 b = mod(uv - h, r) - h;
col.rg = length(a) < length(b) ? a : b;
fragColor = vec4(col,1.0);
}
なにが起きているかは以下の図を見てください。
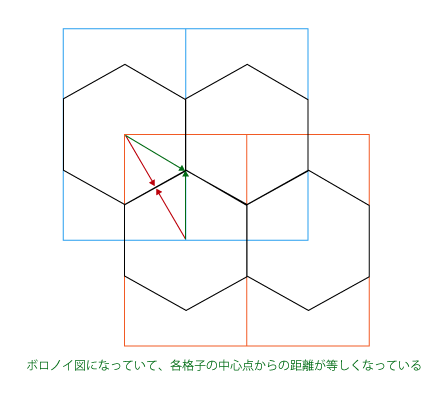
イメージはボロノイ図です。
緑と赤のベクトルを見てもらうと、それぞれのベクトルの長さ(つまり六角形の辺までの距離)がそれぞれの格子中心から同じになっているのが分かります。
ボロノイ図についてをWikipediaから引用すると以下のように書かれています。
ボロノイ図(ボロノイず、英語: Voronoi diagram)は、ある距離空間上の任意の位置に配置された複数個の点(母点)に対して、同一距離空間上の他の点がどの母点に近いかによって領域分けされた図のことである。特に二次元ユークリッド平面の場合、領域の境界線は、各々の母点の二等分線の一部になる。母点の位置のみによって分割パターンが決定されるため、母点に規則性を持たせれば美しい図形を生み出すことが可能。
つまり、各グリッドの中心点から六角形を形成する辺までの距離がすべてのグリッド間で同一距離に保たれている、ということですね。
ちなみにグリッドが正方形ではないのは以下のようにmod関数の第二引数がnormalize(vec2(1.0, 1.73))と非対称な値で繰り返されているからですね。
vec2 r = normalize(vec2(1.0, 1.73));
vec2 h = r * 0.5;
vec2 a = mod(uv, r) - h;
vec2 b = mod(uv - h, r) - h;
そしてこのマジックナンバーは、内積を取るためのベクトルで出てきた三角形の比率を用いたものです。
ボロノイ図的な計算を行っているのは以下の箇所です。
col.rg = length(a) < length(b) ? a : b;
lengthで長さを図り、小さい方を採用することで前段の絵を表示しているわけです。
六角形のタイリングにIDを振る
前節で六角形のタイリングを行いました。
タイリングするだけならこれでも問題ありませんが、なにかしらのランダム要素を入れたり、あるいは(冒頭の絵のように)放射状に色を変化させたり、といったことをしたい場合は各タイルごとにユニークなIDを振ることで実現できます。
実はIDの生成は意外と簡単です。以下のコードを見てください。
vec2 gv = length(a) < length(b) ? a : b;
vec2 id = uv - gv;
col.rg = id * 0.2;
これを実行すると以下のような絵になります。

見事に各六角形ごとに色が変化していくのが視覚化されました。
IDの計算はvec2 id = uv - gv;だけです。非常にシンプルですね。
なぜこれが成り立つかは、uvとgvの値がどうなっているかを考えるとすぐに分かります。
結局、gvの値はuvの値をmodで繰り返しているだけなので、値の変化の比率は変わりません。
結果、整数部分だけが残りIDとして利用できる、というわけなのです。
各六角形のCoordinateを考える
次に、各六角形内の座標系を考えます。
特に重要なのはyの値です。
以下のコードを見てください。
vec4 hexCoords(vec2 uv)
{
vec2 r = vec2(1.0, 1.73);
vec2 h = r * 0.5;
vec2 a = mod(uv, r) - h;
vec2 b = mod(uv - h, r) - h;
vec2 gv = length(a) < length(b) ? a : b;
vec2 id = uv - gv;
float x = atan(gv.x, gv.y);
float y = 0.5 - hexDist(gv);
return vec4(x, y, id);
}
これを視覚化すると以下のようになります。

六角形の中心からぐるっと値が変化しているのが見て取れると思います。
yの値は六角形縁までの距離
やっていることはまず、yの値は六角形の縁までの距離です。
コードは以下ですね。
float y = 0.5 - hexDist(gv);
ここで使われているhexDistは以下のように定義されています。
float hexDist(vec2 p)
{
p = abs(p);
float d = dot(p, normalize(vec2(1.0, 1.73)));
return max(d, p.x);
}
冒頭で紹介した、六角形を描き出すための計算ですね。ここでこれが役に立つわけです。
そして最後に、0.5から縁までの距離を引いた値をyの値として採用しています。
0.5から引いているのは、最大値が(ボロノイ図の性質的に)0.5が最大値となるから、でしょうか。
(ちょっとここはしっかりと理解しきれていません;)
xの値は六角形の中心からの角度
次はxです。
xは六角形の中心からの角度を利用します。角度の計算にはatan関数が使えます。
以下の部分ですね。
float x = atan(gv.x, gv.y);
atan関数は、与えられたふたつの引数(ベクトルのxとy)からなるベクトルと、原点から右に伸びたベクトル(つまりvec2(1, 0))との成す角をラジアンで返してくれる関数です。
なのでgv座標の値を利用して角度を計算している、というわけですね。
hexCoordsのyの値を用いてエッジを出す
次は六角形にエッジをつける処理です。
まずはコードを。
float c = smoothstep(0.0, 0.02, hc.y);
col += c;
これを視覚化すると以下のようになります。

smoothstepは前述のstep関数と似たような動きをします。つまり、edgeに指定された値と比較して、以下なら0.0を、以上なら1.0を返します。
しかしsmoothと名がつく通り、0.0か1.0かという2値化ではなく、スムーズに値を変化させてくれる点が異なります。
ドキュメントを見ると、
smoothstep performs smooth Hermite interpolation between 0 and 1 when edge0 < x < edge1. This is useful in cases where a threshold function with a smooth transition is desired. smoothstep is equivalent to:
genType t; /* Or genDType t; */
t = clamp((x - edge0) / (edge1 - edge0), 0.0, 1.0);
return t * t * (3.0 - 2.0 * t);
Results are undefined if edge0 ≥ edge1.
という計算を行った結果、とされています。
ただ数式を見ただけだとイメージしづらいと思うので、実際にグラフを見てもらうと分かりやすいでしょう。
こちらの記事にグラフが掲載されているので興味がある人は見てみてください。
さて、ではなぜこれを利用すると上のようなきれいな六角形の枠が表示されるのか。
ポイントは、smoothstepに渡している引数の値です。
第三引数が評価する値となっていますが、渡している値はhc.y、つまり六角形の縁までの距離です。
それをsmoothstepによって変化させることで枠を表示している、というわけです。
第一引数が0.0、第二引数が0.02なので、つまり0.0以下は0.0、0.02以上の値は1.0になるわけです。
そしてhc.yの値は縁に近づくほど0.0に近づいていくので、結果として六角形の縁に付近でsmoothstepが適用され、上の図のような枠が表示される、というわけなんですね。
中心から波状にエフェクトを掛ける
最後に解説するのは冒頭の動画にあるように、中心から波状エフェクトを出す方法です。
これもコードから見てみます。
vec4 hc = hexCoords(uv);
float time = iTime * 0.5;
float wavy = pow(sin(length(hc.zw) - time), 4.0) + 0.1;
float c = smoothstep(0.0, 0.02, hc.y);
col = vec3(c * wavy);
重要なポイントは以下の部分だけです。
float wavy = pow(sin(length(hc.zw) - time), 4.0) + 0.1;
hc.zwは前節でIDだと解説しました。
つまり、length(hc.zw)はIDに基づいて変化していきます。そしてそれは中心から値が徐々に大きくなっていくものでもあります。
そしてそこからtimeを引き、さらにそれをsinによって値を変化させます。
またlength(hc.zw)はUV単位ではなく六角形単位で増えていくので、結果的に下のような結果が得られる、というわけです。
レイマーチの平面に描く
少しだけ補足です。
冒頭の絵はレイマーチングして現れた平面に対して今回の方法を使って絵を作っていました。
ただ今回はレイマーチングの解説ではないので詳細は割愛します。
レイマーチングについては以前、入門記事([GLSL] レイマーチング入門 vol.1)を書いたのでそちらをご覧ください。
レイマーチした結果部分のコードだけを抜粋します。
if (d < 0.01)
{
vec2 st = p.xz;
vec4 hc = hexCoords(st);
float time = iTime * 5.0;
float l = pow(sin((length(hc.zw) - time) * 0.3), 4.0);
vec3 c = vec3(S(0.01, 0.03, hc.y));
float f = exp(-t * 0.08);
col.rgb = c * l * f;
}
d < 0.01の場合なのでつまりはレイマーチングで平面が表示されるべきとき、ということですね。
そしてその中の処理を見てみると今まで解説してきた内容とほぼ同じなことが分かると思います。
唯一違う点はuvを使う代わりにレイマーチした結果のp.xzを利用している点です。
平面にぶつかったレイの位置の、XZ平面の位置をそのままUVとして利用しているわけですね。
これがそのままUVの値として利用できるというわけです。
まとめ
分かってしまえば原理はそこまでむずかしくありません。
IDをhash関数に渡すとランダムな値を得ることもできるので、それを元に色を変化させたり、としても面白いでしょう。
ちなみにこのレイマーチングの平面への描画を工夫すると以下のような絵を作り出すこともできます。

ぜひ色々工夫してみてください。