C言語で任意中心回転する四角形の描画

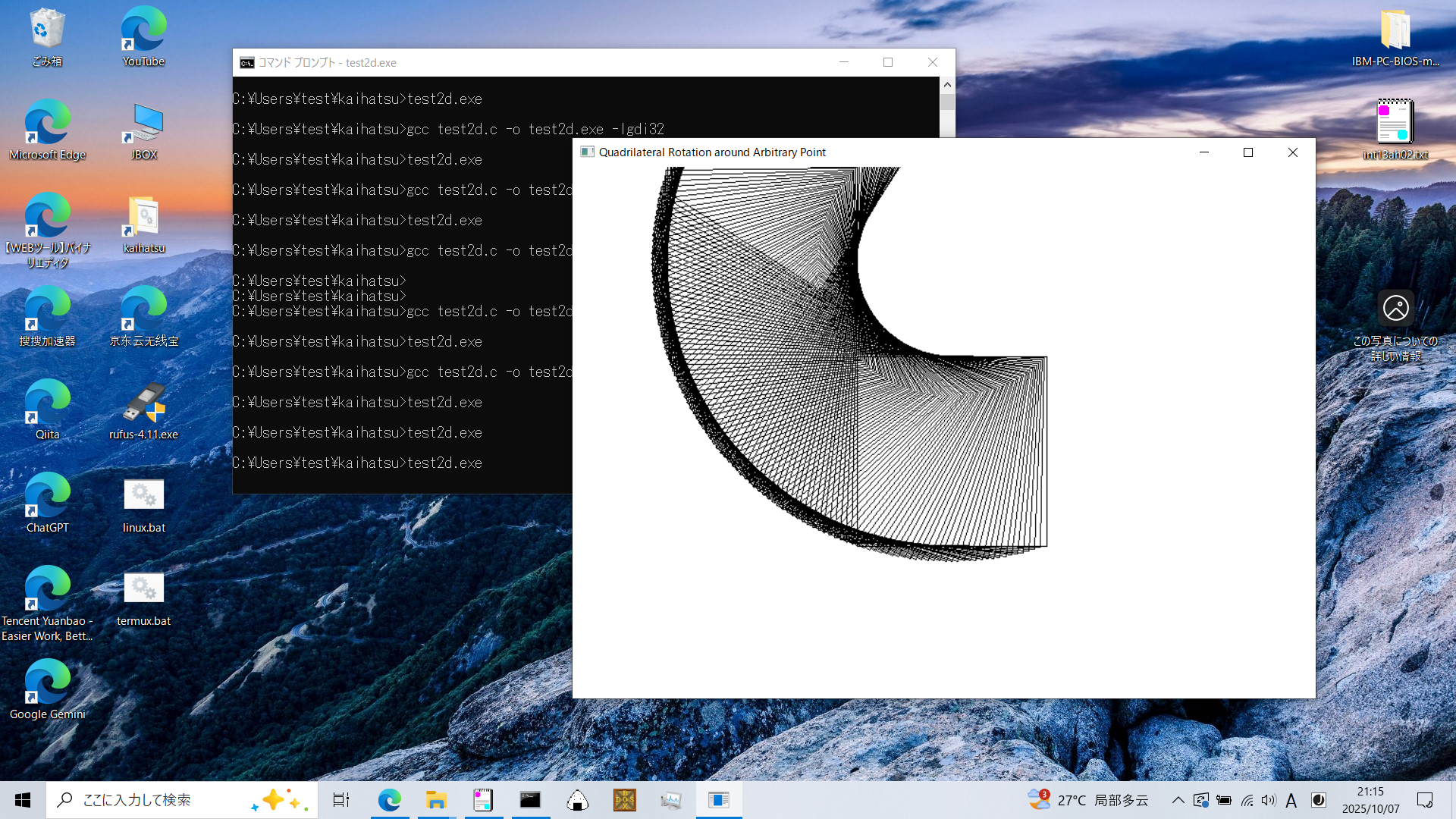
初めに

アフィン変換と回転行列を用いて任意の点を中心に回転させます。

回転行列及び任意の点を中心に回転させる公式の導出は以下の通りです。

アフィン変換について参考にしたサイト
このサイトの説明が直感的で分かり易いです。
https://youta-blog.com/rotate_point/

C言語で実装

test2d.c

// gcc test2d.c -o test2d.exe -lgdi32
#include <windows.h>
#include <math.h>

#define WIDTH 800
#define HEIGHT 600

float theta = 0.0f;  // 回転角度

// 四角形の頂点（画面上の座標）
float verts[4][2] = {
    {300, 200}, // 左上
    {500, 200}, // 右上
    {500, 400}, // 右下
    {300, 400}  // 左下
};

// 回転中心（画面上の任意の点）
float ox = 400.0f; // 回転中心X
float oy = 100.0f; // 回転中心Y

LRESULT CALLBACK WndProc(HWND hwnd, UINT msg, WPARAM wParam, LPARAM lParam) {
    static HDC hdc;
    static PAINTSTRUCT ps;

    switch (msg) {
    case WM_PAINT: {
        hdc = BeginPaint(hwnd, &ps);

        POINT pts[5]; // 描画用（最後は始点に戻す）

        for (int i = 0; i < 4; i++) {
            float x = verts[i][0];
            float y = verts[i][1];

            // 回転中心に対して相対座標に変換
            float x_rel = x - ox;
            float y_rel = y - oy;

            // 回転行列を適用
            float x_rot = x_rel * cos(theta) - y_rel * sin(theta);
            float y_rot = x_rel * sin(theta) + y_rel * cos(theta);

            // 元の位置に戻す
            pts[i].x = (LONG)(x_rot + ox);
            pts[i].y = (LONG)(y_rot + oy);
        }

        pts[4] = pts[0]; // 始点に戻す
        Polyline(hdc, pts, 5);

        EndPaint(hwnd, &ps);
        break;
    }
    case WM_DESTROY:
        PostQuitMessage(0);
        break;
    default:
        return DefWindowProc(hwnd, msg, wParam, lParam);
    }

    return 0;
}

int WINAPI WinMain(HINSTANCE hInstance, HINSTANCE hPrevInstance,
                   LPSTR lpCmdLine, int nCmdShow) {

    const char CLASS_NAME[] = "RotateArbitraryCenterClass";

    WNDCLASS wc = {0};
    wc.lpfnWndProc = WndProc;
    wc.hInstance = hInstance;
    wc.lpszClassName = CLASS_NAME;

    RegisterClass(&wc);

    HWND hwnd = CreateWindowExA(
        0, CLASS_NAME, "Quadrilateral Rotation around Arbitrary Point",
        WS_OVERLAPPEDWINDOW, CW_USEDEFAULT, CW_USEDEFAULT,
        WIDTH, HEIGHT, NULL, NULL, hInstance, NULL);

    ShowWindow(hwnd, nCmdShow);
    UpdateWindow(hwnd);

    MSG msg;
    while (1) {
        if (PeekMessage(&msg, NULL, 0, 0, PM_REMOVE)) {
            if (msg.message == WM_QUIT) break;
            TranslateMessage(&msg);
            DispatchMessage(&msg);
        } else {
            theta += 0.02f; // 回転速度
            if (theta > 2 * M_PI) theta -= 2 * M_PI;

            InvalidateRect(hwnd, NULL, TRUE);
            Sleep(16); // 約60fps
        }
    }

    return 0;
}

Polyline関数

pts[0]----pts[1]
 |          |
 |          |
pts[3]----pts[2]

pts は四角形の頂点（角の座標）を入れる配列です。
四角形の頂点は pts[0]、pts[1]、pts[2]、pts[3] の4つ。
最後に pts[4] = pts[0] を入れることで、pts[2]→pts[3]→pts[0] の線が引かれ、四角形が閉じます。

BOOL Polyline(
  HDC       hdc,   // 描画先
  const POINT *lppt,// 線で結ぶ点の配列
  int       cPoints // 配列の点の数
);

typedef struct tagPOINT {
    LONG x;
    LONG y;
} POINT;

POINT pts[5];
pts[0].x = 100; pts[0].y = 100;
pts[1].x = 200; pts[1].y = 100;
pts[2].x = 200; pts[2].y = 200;
pts[3].x = 100; pts[3].y = 200;
pts[4] = pts[0]; // 始点に戻す

Polyline(hdc, pts, 5); // 順に線を結ぶ

動作確認