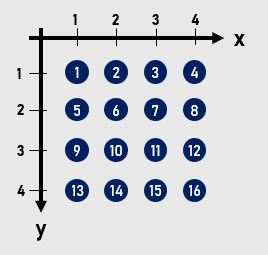
こんにちは、高校 2 年生の E869120 です。
私は、最近「碁盤目状道路の最適化」という研究を行いました。スーパーコンピューターなどを用いて計算を行い、最終的には京都のような碁盤の目を13.9%効率化することに成功しました。本記事では、その研究をすべて公開します。
1. はじめに
皆さん、碁盤の目状の道路をご存知でしょうか。例えば、
などが有名です。

(「これが本当の碁盤の目。上空からみたバルセロナが芸術的すぎる」より引用)
研究のきっかけ
私は 2019 年の 8 月、京都に行き、碁盤の目状の道路を歩きました。そこで、
京都のような碁盤の目状の道路網は、あまり便利な道路網とはいえないのではないか。
と感じました。何故そのように感じたのでしょうか?
碁盤の目はなぜ不便なのか?
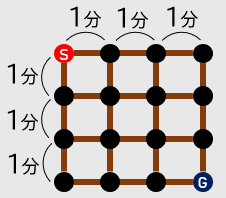
そこで、以下の 4×4 の碁盤の目状の道路網を考えてみましょう。左上の交差点から右下の交差点まで移動することを考えます。また、隣接する交差点間の移動に 1 分かかるものとします。
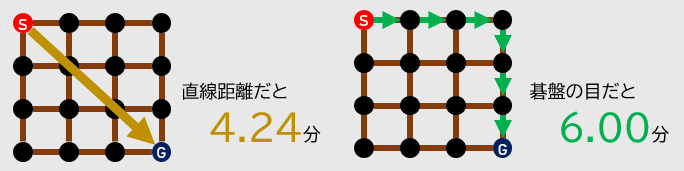
もし直線距離で移動できる場合、$3\sqrt{2}≒4.24$ 分で移動できます。しかし、碁盤の目上を動くとなると、最短でも 6 分かかってしまうのです。つまり、碁盤の目の方が 41% も移動時間が多くなってしまうのです。これこそが、不便だと思った理由です。
そこで研究が始まった
私は、夏休みに京都の街を歩いて感じたことをきっかけに、
「碁盤の目より便利な道路網があるのではないか」
と考えました。そこで、
- 「便利な道路網の条件」を考え、
- コンピューターを使って碁盤の目より便利な道路網を構成する
ことにしました。私は、様々なアルゴリズムや最適化の手法を用い、最終的にはスーパーコンピューターによる並列化計算を使い、研究を行いました。
目次
| 章 | タイトル | 備考 |
|---|---|---|
| 1. | はじめに | |
| 2. | 本研究で解く問題 | |
| 3. | 本論Ⅰ ~碁盤の目を改善する~ | 本記事のメインコンテンツです |
| 4. | 見えた課題・改善点 | |
| 5. | 本論Ⅱ ~より便利な道路網を作る~ | 4 章の課題を克服した結果を書きます |
| 6. | 碁盤の目をさらに効率化する | 本研究の最先端のところまで行きます |
| 7. | 結論 | |
| 8. | おわりに | |
| 9. | 謝辞 | |
| 10. | 参考文献 |
2. 本研究で解く問題
「いざ研究しよう!」と思っても、条件や設定を決めないと何も始まりません。
まずは研究を分かりやすくするために、「一つの問題」に落とし込むことにしました。
問題設定
縦 $N$ 行・横 $N$ 列の大きさの碁盤の目があります。隣り合う交差点間の距離は 1 です。つまり、交差点が合計で $N^2$ 個あり、それぞれ座標 $(1, 1), (1, 2), ..., (1, N),$ $(2, 1), (2, 2), ..., (N, N-1), (N, N)$ に位置すると考えることもできます。
あなたは、碁盤の目の交差点の位置は変えずに、道路の並びのみを変えることができます。上手く道路の並びを変えることで、できるだけ「便利」な道路網を建設してください。
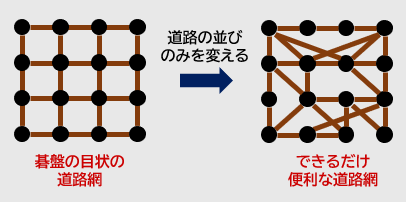
「便利な道路網」って何?
私は、以下の 2 つの条件を満たす道路網が「便利」だと考えました。
条件1
最短距離の合計値ができるだけ小さい。
つまり、交差点 $u$ と $v$ の間の最短距離を $dist(u, v)$ とするとき、
$$\sum_{i=1}^{N^2}{\sum_{j=i+1}^{N^2}} dist(i, j) = dist(1, 2) + dist(1, 3) + ... + dist(N^{2}-1, N^{2})$$ の値ができるだけ小さい。(最短距離の定義についてはこちらで後述)
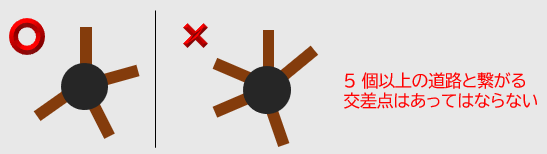
条件2
どの交差点も、高々 4 本の道路と繋がっている。
※ この条件を入れた理由は、道路網は空港ではないからです。ハブ空港のように数十本の道路と繋がっている「ハブ交差点」を作るのは現実的ではないと考えられます。
補足:N の大きさについて
本研究では、$N = 30$ とし、30×30の道路網を考えました。
理由としては、「京都の碁盤の目」が19×21程度であり、それより少し大きいものを考えれば十分なのではないか、と考えたからです。

(「京の通り名 わらべ唄」より参照)
補足:最短距離の定義
ここでは、最短距離は以下のように定義されます。
通った道路の長さの合計が最短となるような経路(最短経路)における、通った道路の長さの合計。ただし、すべての道路は直線距離で 2 都市間を結ぶものとする。
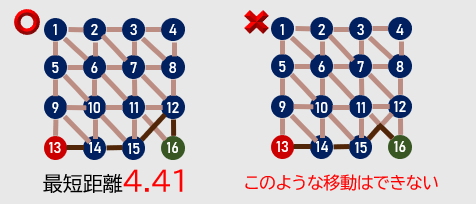
例えば、下図において、交差点 13 から交差点 16 までの最短経路は濃い茶色で書かれている経路であり、最短距離は $1+1+\sqrt{2}+1≒4.41$ です。また、一部の道路が立体交差や地下道であることが考えられるので、下図の右側のように、交差点以外の場所で曲がるような移動はできません。
3. 本論Ⅰ ~碁盤の目を改善する~
私は、2 つのステップで研究を行いました。
ステップ 1| 規則的で単純な道路網を頭で考える
ステップ 2| スパコンを使い、ステップ 1 で得られた道路網をさらに改善する
本記事では、以下の 3 つを順に紹介します。
3-0. 碁盤の目の場合
30×30 の碁盤の目の場合、最短距離の合計値は 8,091,000 となります。
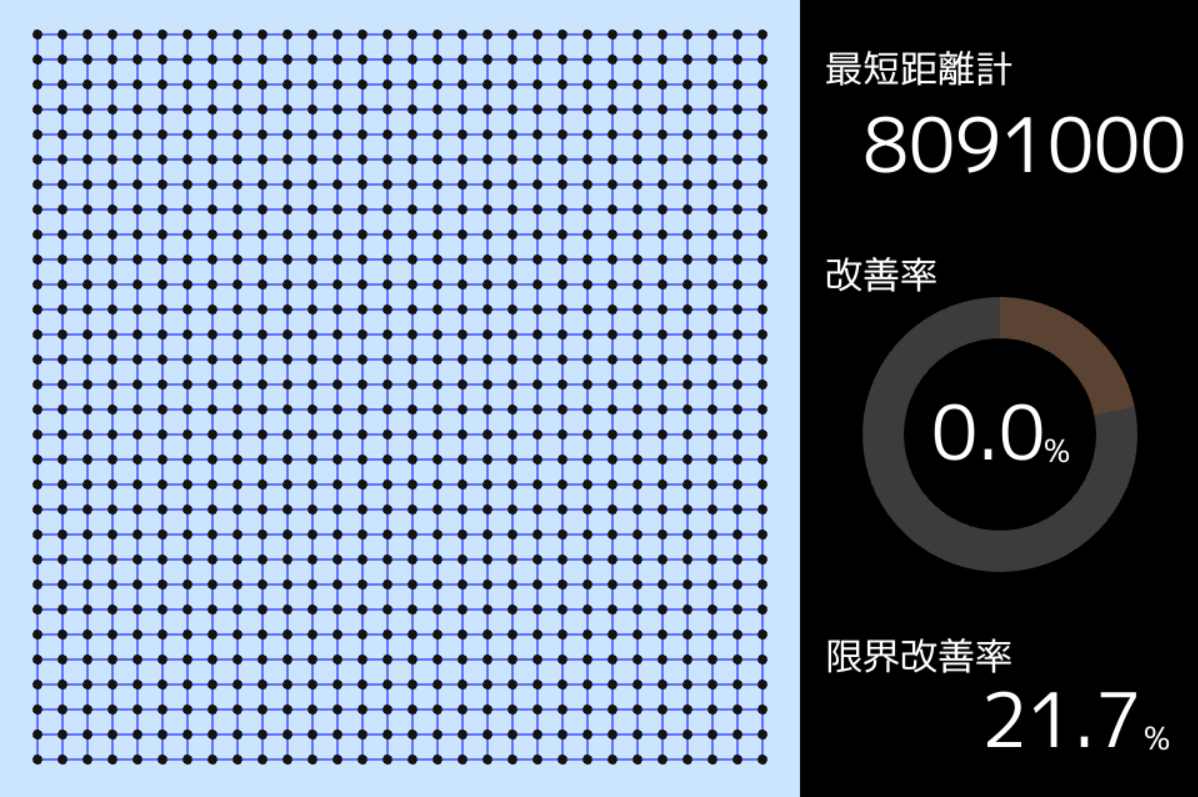
以後、改善率を以下のように定義します。
$$改善率 = \frac{碁盤目道路の最短距離合計値 - 改善した道路網の最短距離合計値}{碁盤目道路の最短距離合計値}×100$$
なお、全交差点対において直線距離で移動できた場合、改善率は21.7%(これを限界改善率とする)となりますが、各交差点に 4 つしか道路を繋いではならない制約があるため、改善率 21.7% となるような道路網は存在しません。
3-1. ステップ1: 規則的で単純な道路網を頭で考える
まず、単純な道路網について考えていきます。3 通り思いつきましたので、その 3 通りを紹介します。
| 方法 | タイトル | 改善率 |
|---|---|---|
| 方法 A | 3 列ずつ分ける | ??.?% |
| 方法 B | 1 行ごとにずらす | ??.?% |
| 方法 C | 方法 A と B を合成させる | ??.?% |
方法 A: 3 列ずつ分ける
- 全ての行に、横の道路が存在する。
- 1, 4, 7, 10, 13, 16,... 列目に、つまり 3 列ごとに縦の道路が存在する。
- 2 つの縦線の間に斜めの道路が 2 つ存在し、それらがクロスのような形になっている。
その 3 つの特徴を持った単純な道路網の場合、最短距離の合計値が 7,462,761 となり、改善率 7.8% が達成できます。詳しくは、下の図をご覧ください。

方法 B: 1 行ごとにずらす
- 全ての行に、横の道路が存在する。
- 1 列目と $N$ 列目に縦の道路が存在する。
- $i$ 行目 $j$ 列目の交差点を $(i, j)$ とするとき、$i+j$ が偶数の場合に限り、以下の道路が存在する。
- $(i, j)$ と $(i+1, j+1)$ を繋ぐ道路。
- $(i, j+1)$ と $(i+1, j)$ を繋ぐ道路
その 3 つの特徴を持った単純な道路網の場合、最短距離の合計値が約 7,366,442 となり、改善率 9.0% が達成できます。詳しくは、下の図をご覧ください。

方法 C: 「3 列ごとに分ける」と「行ごとにずらす」を合成させる
方法 A と方法 B は全然違いますが、それぞれ改善率 7.8%・9.0% と、碁盤の目と比較すればとても便利です。そこで、2 つの方法を合成させることを考えました。具体的には、以下の方法です。
- 全ての行に、横の道路が存在する。
- $i$ 行目 $j$ 列目の交差点を $(i, j)$ とするとき、$i+j$ が 3 で割って 2 余る場合に限り、
- $(i, j)$ と $(i+1, j)$ を繋ぐ道路
- $(i, j+1)$ と $(i+1, j+2)$ を繋ぐ道路
- $(i, j+2)$ と $(i+1, j+1)$ を繋ぐ道路 が存在する。
これは、一行ごとに切って見ると、方法 A の「3 列ごとに分ける」が利用されているように見えますが、全体を見渡すと、方法 B の「1 行ごとにずらす」が利用されています。
その 2 つの特徴を持った単純な道路網の場合、最短距離の合計値が 7,259,573 となり、改善率 10.3% が達成できます。以前 2 つの方法と比べて便利さが増しています。

節のまとめ
| 方法 | タイトル | 改善率 |
|---|---|---|
| 方法 A | 3 列ずつ分ける | 7.8% |
| 方法 B | 1 行ごとにずらす | 9.0% |
| 方法 C | 方法 A と B を合成させる | 10.3% |
改善率 10.3% の道路網までは自力で思いつくことができました。(思いつくのに 2 時間くらいかかりました)
しかし、ここから先は自分の頭では思いつきませんでした。
3-2. ステップ2: スパコンを使い、道路網をさらに改善する
ここからは、ステップ 1 の方法 C で得られた改善率 10.3% の道路網を、コンピューターを使ってさらに改善することにしました。本記事では、
の 3 つに分けて説明します。
全体のアルゴリズム
私が用いたのは、「山登り法」というアルゴリズムです。山登り法を使うと、以下のように道路網が少しずつ変更され、少しずつ改善されていきます。
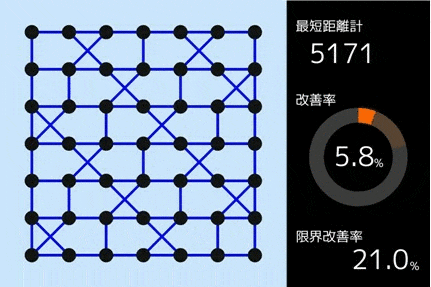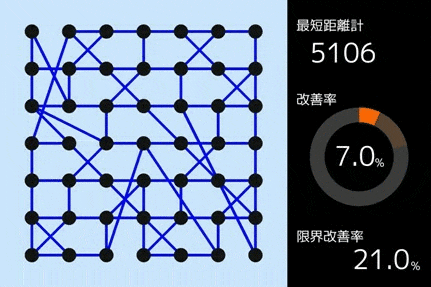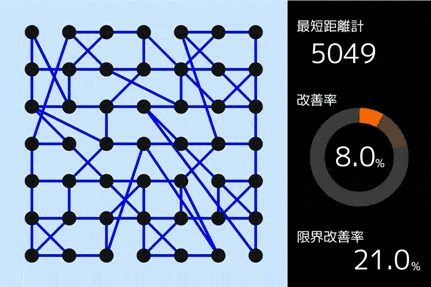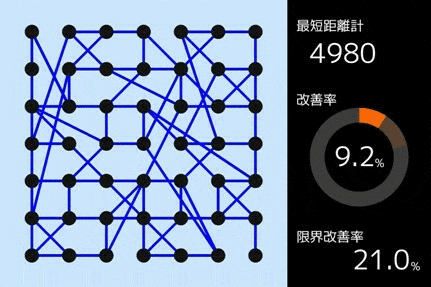
具体的には、以下のようなアルゴリズムを用いました。(やや難しめです。読み飛ばしても構いません。)
- 初期解を生成する。ここでは、初期解は前節の方法 C で得られた改善率 10.3% の道路網とする。
- 以下の操作を 30,000 回繰り返す。1
- 道路に以下の変更を行う。
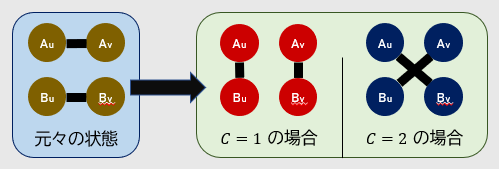
- 2 つの道路 $A$, $B$ をランダムに選ぶ。道路 $A$ は交差点 $A_u$ と $A_v$ の間を結んでいるものとし、道路 $B$ は交差点 $B_u$ と $B_v$ の間を結んでいるものとする。{$A_u, A_v, B_u, B_v$} は全て異ならなければならない。
- 整数 $C$ をランダムに選ぶ。50% の確率で $C=1$、そうでない場合 $C=2$ とする。
- $C=1$ のとき、既存の 2 つの道路を消し、$(A_u, B_u)$ 間を結ぶ道路と $(A_v, B_v)$ 間を結ぶ道路を建設する。
- $C=2$ のとき、既存の 2 つの道路を消し、$(A_u, B_v)$ 間を結ぶ道路と $(A_v, B_u)$ 間を結ぶ道路を建設する。
- 変更した後の道路網における、最短距離合計値を求める。
- その変更によって、最短距離合計値が小さくなった場合、その変更を採用する。
- そうでない場合、その変更を採用せず、道路網を元に戻す。
- 道路に以下の変更を行う。
※ このアルゴリズムで改善を行っても、各交差点から出る道路の本数(グラフ理論用語でいえば、頂点の次数)が変わることはないため、「便利な道路網の条件」が満たされた状態で道路網が変更されていきます。
最短距離合計値を求めるアルゴリズム
さて、どのようにして最短距離合計値を求めたのでしょうか。
私が用いたアルゴリズムは「ダイクストラ法」というアルゴリズムです。
ダイクストラ法を使うと以下の計算ができます。
$V$ 個の交差点と $E$ 本の道路があったとき、そして $dist(u, v)$ を交差点 $u$ から交差点 $v$ までの最短距離とするとき、$dist(u, 1), dist(u, 2), dist(u, 3), ..., dist(u, N)$ の値を $O(E \ log \ V)$ で求めることができる。そのため、最短距離の合計値を $O(VE \ log \ V)$ で求めることができる。
本研究の問題では、$V = N^2$、$E = 2N^2$ 程度であるため、$O(N^4 \ log \ N)$ で最短距離合計値を求めることができます。
ダイクストラ法がどのようなアルゴリズムであるか知りたい方は、以下の記事をお読みください。
また、計算量 (O 記法、$O(E \ log V)$ など) についてわからない方は、以下の記事をお読みください。
結果
その 2 つのアルゴリズムを用いて、3-1. 節の方法 C で得られた**改善率 10.3%**の道路網をさらに改善してみました。その結果、以下のようになりました。
| 環境 | プログラミング言語 | 実行時間 | 最短距離合計値 | 改善率 |
|---|---|---|---|---|
| ノートパソコン | C++ | 1時間10分 | 6,947,153 | 14.1% |
| スパコン | CUDA | 1時間37分 | 6,865,560 | 15.1% |
| ※スーパーコンピューターによる計算では Tesla V100 を使用。 |
また、スパコンによる計算で得られた改善率 15.1% の道路網は以下のようになりました。

ソースコード
※ 並列化環境で高速に実行するため、CUDA ソースコードでは山登り法を工夫して使っており、2 ダイクストラ法の代わりにベルマンフォード法を応用したものを使っております。3 字面の関係上、詳しいアルゴリズムの説明は省略させていただきます。(詳しくは脚注参照)
4. 見えた課題・改善点
スパコンを使って計算を行った結果、改善率 15.1% の道路網を得ることができました。しかし、その道路網を見てください。

**これはとても複雑です。**もはや道路網ではありません。まず建設がとても難しく、仮に現代の最新技術を使って建設できたとしても莫大な費用がかかってしまいます。そして完成したとしても、立体交差する個数がとても多くなり、ジェットコースターのようにアップダウンの大変激しい道路網になってしまい、徒歩はもちろん、車でも移動するのが難しくなってしまいます。
このままの状態だと、「便利な道路網」の条件を満たしていながら、「便利な道路網」ではなくなってしまいます。どのようにすればよいのでしょうか。
道路網が複雑に見える原因を分析してみた
まず、道路網がなぜ複雑になるか、原因を究明することにしました。そして見つかった理由は、以下のようになります。
- 道路網の左端から右端まで伸びる、長さ30を超えるとても長い道路が数十本あること
左端から右端だけでなく、上端から下端まで伸びる道路もたくさんありました。
そして追加した 3 つ目の条件
そこで私は、2 章で述べた便利な道路網の条件に、以下の条件を追加しました。
- 全ての道路は、長さ $\sqrt{2}$ 以下でなければならない。
つまり、新しい「便利な道路網の条件」は、以下の 3 つということになります。
- どの交差点も、高々 4 本の道路と繋がっていなければならない。
- どの道路も、長さ $\sqrt{2}$ 以下でなければならない。
- 前述の 2 つの条件を満たす道路網の中で、最短距離の合計値ができるだけ小さくなければならない。
5. 本論Ⅱ ~より便利な道路網を作る~
追加した 3 つ目の条件をもとに、3-1. 節の方法 C で得られた**改善率 10.3%**の道路網をさらに改善することにしました。なお、改善率 10.3% の規則的な道路網において、すべての道路の長さは $\sqrt{2}$ 以下であるため、「新・便利な道路網の条件」を満たします。
利用したアルゴリズム
3 章で、古い条件で道路網の改善を行ったときと同様、
を利用しました。
結果
| 環境 | プログラミング言語 | 実行時間 | 最短距離合計値 | 改善率 |
|---|---|---|---|---|
| ノートパソコン | C++ | 30分 | 7,078,586 | 12.5% |
| スパコン | CUDA | 33分 | 7,014,442 | 13.3% |
| ※スーパーコンピューターによる計算では Tesla V100 を使用。 |
そして、スパコンによる計算で得られた改善率 13.3% の道路網は、以下のようになります。

6. 碁盤の目をさらに効率化する
前章で述べたように、スーパーコンピューターで 30 分計算させることで、改善率 13.3% の道路網を得ることができました。
確かにそれで十分かもしれませんが、さらに改善して少しでも理論値に近づけたかったので、新たな改善の手法を考えることにしました。そこで思いついたのは、2 つの方法です。
6-1. ポイント 1: 山登り法から焼き鈍し法への転換
先程述べた山登り法でも十分な解を得ることができますが、一つ欠点があります。これは局所的最適解に陥ってしまうことです。
山登り法の欠点
分かりやすく説明するために、関数 $f(x)$ があって、できるだけ $f(x)$ の値が最大となるような $x$ を見つけることを考えましょう。
例えば、$x=1$ から始め、$x$ の値を 0.1 動かすことで解が良くなったらそれを採用する、という山登り法のアルゴリズムを利用すると、以下の GIF 画像のようになります。
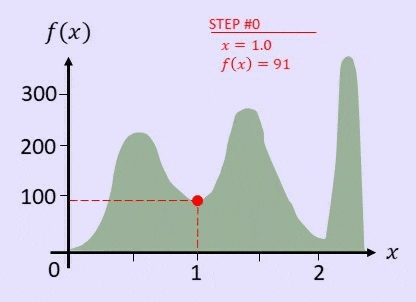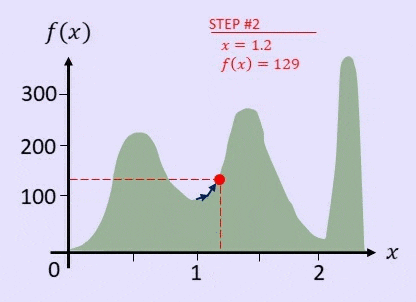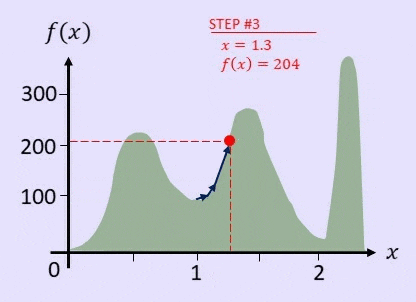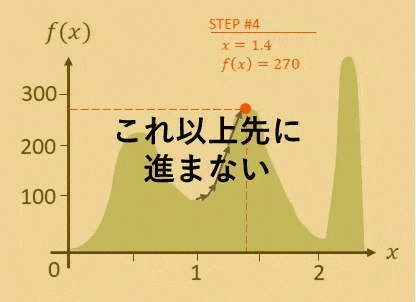
そのように、局所的最適解に陥ってしまった場合、一回悪い方向に解をもってこないと、最適な解が出せないというパターンが起こります。
焼き鈍し法とは(やや難しめ)
その「局所的最適解」に陥る問題を解決してくれるアルゴリズムが「焼き鈍し法」です。単純に書くと、以下のようなアルゴリズムです。(以下の説明では、本研究の問題に合わせて、評価関数が小さい方を「良い」とします。)
- 定数 $a, b$ を決める。
- 山登り法と同様、(道路網などに)微妙な変更を行ってみる。
- 変更前の評価関数(今回解く問題だと最短距離合計値)を $s_1$、変更後の評価関数を $s_2$ とする。
- $s_2-s_1 \leq a \times e^{bt}$ の場合、変更を採用する。そうでなければ、変更を採用しない。
- ただし、$t$ はこの段階で変更が連続で採用されなかった回数とする。例えば、1 回前の変更が採用された場合、$t=0$ となる。
そうすると、局所的最適解に陥った場合など、連続して変更が採用されなかった場合においても、**「一旦解を悪くしてから、別のより良い解の方向に進む」**という戦略を利用することができるので、山登り法に比べて良い解が得られる可能性が高いです。
6-2. 最短経路アルゴリズムの高速化(かなり難しめ)
これまで使ってきたダイクストラ法というアルゴリズムを使うと、大きさ $N \times N$ で高々 $2N^2$ 本の道路から成る道路網における最短距離合計値を求めるのに、計算量 $O(N^4 \ log N)$ かかります。
しかし「辺の長さが $1$ か $\sqrt{2}$ の二種類しかない」という特殊な条件を使えば、$O(N^4)$ で最短距離合計値を求めることができるのです。ここでは、交差点 $s$ からスタートし、$dist_i$ を交差点 $s$ から交差点 $i$ までの距離とするとき、$dist_1, dist_2, ..., dist_{N^2}$ を計算量 $O(N^2)$ で求めるアルゴリズムを紹介します。
-
待ち行列(キュー)を 2 つ用意する。それぞれ $Q_1, Q_2$ とする。
- キューには (距離, 交差点番号) の組が、距離の小さい順に入っていることが想定されている。
- 初期化を行う。
- まず、$i = 1, 2, 3, ..., N^{2}$ について、$dist_i = \infty$ とする。
- 次に、$dist_s = 0$ とし、$Q_1, Q_2$ 両方に組 $(0, s)$ を入れる。
- $Q_1$ の先頭要素の距離を $D_1$、$Q_2$ の先頭要素の距離を $D_2$ とする。
- $D_1 + 1 \leq D_2 + \sqrt{2}$ の場合
- $Q_1$ の先頭要素を取り除く。取り除いた $Q_1$ の先頭要素における交差点番号を $v_1$ とする。
- 交差点 $v_1$ から、長さ 1 の道路で直接つながっている交差点を $w_1, w_2, w_3, ..., w_F$ とする。そのとき、$i = 1, 2, 3, ..., F$ について、$dist_{w_i} > D_1 + 1$ であれば、$dist_{w_i}$ を $D_1 + 1$ に更新し、$Q_1, Q_2$ の両方に $(D_1 + 1, w_i)$ を入れる。
- $D_1 + 1 > D_2 + \sqrt{2}$ の場合
- $Q_2$ の先頭要素を取り除く。取り除いた $Q_2$ の先頭要素における交差点番号を $v_2$ とする。
- 交差点 $v_2$ から、長さ $\sqrt{2}$ の道路で直接つながっている交差点を $x_1, x_2, x_3, ..., x_G$ とする。そのとき、$i = 1, 2, 3, ..., G$ について、$dist_{x_i} > D_2 + \sqrt{2}$ であれば、$dist_{x_i}$ を $D_2 + \sqrt{2}$ に更新し、$Q_1, Q_2$ の両方に $(D_2 + \sqrt{2}, x_i)$ を入れる。
- $D_1 + 1 \leq D_2 + \sqrt{2}$ の場合
上のようなアルゴリズムを用いると、$Q_1, Q_2$ は必ず距離の小さい順になります。そのため、ダイクストラ法で用いる優先度付きキューと同じような効果を持つことができます。
分かりやすく説明したつもりですが、この記事に書かれているアルゴリズムの中で最も難しいところですので、理解できなくてもお許しください。(AtCoder に換算した難易度でいうと**黄色~橙色**レベルだと思います。)
一応、擬似コードは、以下のようになります。(C++ です。)
# include <bits/stdc++.h>
using namespace std;
// 交差点の数
int N;
// 最短距離
double dist[909];
// 道路網(グラフ)のデータ
vector<int> G1[909];
vector<int> G2[909];
double sum_of_shortest_distance() {
double sum = 0.0;
for (int i = 0; i < N; i++) {
for (int j = 0; j < N; j++) dist[j] = 1e9;
dist[i] = 0;
// キューを用意します。
// 実際のコードでは (距離, 頂点番号) を管理しておらず、頂点番号だけを持っています
queue<pair<double, int>> Q1, Q2;
Q1.push(make_pair(0, i));
Q2.push(make_pair(0, i));
while (!Q1.empty() || !Q2.empty()) {
double c1 = 1e9; if (!Q1.empty()) c1 = Q1.front().first + 1.0;
double c2 = 1e9; if (!Q2.empty()) c2 = Q2.front().first + 1.41421356237309;
if (c1 < c2) {
int pos = Q1.front().second; Q1.pop();
for (int t1 : G1[pos]) {
if (dist[t1] > c1) {
dist[t1] = c1;
Q1.push(make_pair(dist[t1], t1));
Q2.push(make_pair(dist[t1], t1));
}
}
}
else {
int pos = Q2.front().second; Q2.pop();
for (int t2 : G2[pos]) {
if (dist[t2] > c2) {
dist[t2] = c2;
Q1.push(make_pair(dist[t2], t2));
Q2.push(make_pair(dist[t2], t2));
}
}
}
}
for (int j = i + 1; j < N; j++) sum += dist[j];
}
return sum;
}
6-3. 結果
「焼き鈍し法」「改良版最短経路アルゴリズム」の 2 つのアルゴリズムを用いて、計算を行った結果、以下のようになりました。
| 環境 | プログラミング言語 | 実行時間 | 最短距離合計値 | 改善率 |
|---|---|---|---|---|
| ノートパソコン | C++ | 1時間20分 | 6,983,308 | 13.7% |
| スパコン | CUDA | 1時間8分 | 6,966,324 | 13.9% |
| ※スーパーコンピューターによる計算では Tesla V100 を使用。 |
なお、スーパーコンピューターでは、前章で最終的に得られた13.3%という結果を、僅か1分35秒の計算で超えていました。また、C++ での最短経路アルゴリズムの計算には、
| 手法 | 計算量 | 実行時間($N = 30$ で実行) |
|---|---|---|
| ダイクストラ法 | $O(N^4 \ log N)$ | 68.079ミリ秒 |
| 改良版アルゴリズム | $O(N^4)$ | 29.823ミリ秒 |
と、実行時間がおよそ5分の2になっていることが分かります。やはり改良版アルゴリズムは高速でした。
最後に、スパコンによる計算で得られた改善率 13.9% の道路網は、以下のようになります。3 章で得られた道路網に比べて遥かに単純であり、遥かに作りやすく、遥かに現実的です。

ソースコード
※ 並列化環境で高速に実行するため、CUDA ソースコードでは焼き鈍し法を工夫して使っています。4 字面の関係上、詳しいアルゴリズムの説明は省略させていただきます。(詳しくは脚注参照)
7. 結論
私は、規則的な道路網で碁盤の目を 10.3% 改善することに成功しました。
私は、スパコンを用いて碁盤の目を 13.9% 改善することに成功しました。
そして、そのどちらも単純な道路網であり、建設がそれほど難しくない道路網となりました。
さて、碁盤の目を 13.9% 改善すると、社会・地球に何が起こるのでしょうか。
13.9% の改善で何が起こるのか
ここでは、以下の条件を仮定するものとします。
| 条件 | 値 |
|---|---|
| 通行者数 | 50,000 人/日 |
| 平均走行距離 | 7km |
| 燃費効率 | 8km/L |
| ガソリン価格 | 154円/L |
| 二酸化炭素排出量 | 2.32kg/L5 |
一つ目に、金の削減です。**ガソリン代だけで、**1 年間で節約できる金は以下のようになります。
$$\left(50000 \times 365 \times \frac{7}{8} \times 154 \right) \times \frac{13.9}{100} ≒ 3.42 \times 10^{8}$$
となり、1 年間で 3.4 億円以上節約できることがわかります。車の維持費用なども考えると、節約できる金額はさらに増えると思います。1 年間だけ見ても建設費用には及びませんが、50 ~ 100 年の長期で見ると 200 億円以上節約できるので、効率的と考えることができます。
二つ目に、二酸化炭素排出量の削減です。1 年間で削減できる CO2 の量は、以下のようになります。
$$\left(50000 \times 365 \times \frac{7}{8} \times 2.32 \right) \times \frac{13.9}{100} ≒ 5.15 \times 10^{6}$$
となり、二酸化炭素を 5150トン削減することができます。それは、今日、日本人 91.6万人が排出した二酸化炭素の量と同じになるのです。6
土地の問題は大丈夫なのか?
道路網を実際に建設したとして、道路ではない「土地」を上手く活用できるのか、家や施設を建設することですべての土地を有効活用できるのか、ということについても考えてみました。
確かに、3 章で求めた改善率 15.1% の複雑な道路網だと、使えないかもしれません。
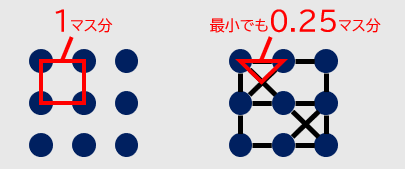
しかし、道路の長さを $\sqrt{2}$ 以下にすると、「1 マス」を最小の正方形区画 1 個分(詳しくは下図参照)とするとき、どのような小さい区画であっても1/4 マス以上の領域を有することが保証されます。そのため、土地を有効活用することは十分に可能と考えられます。
まとめ
碁盤の目の改善を行うことは、予算面でも環境面でも効率的です。
そのため、数学的・情報科学的に考えても、碁盤の目状の道路を改築することは良い選択肢の一つなのではないかと結論付けました。
8. おわりに
本研究の内容は以上となります。
あくまでも高校生の研究、そして普通の高校生が書く記事ですので、現実性に欠けたりするところがあったり、記事中で分かりにくい部分があったりするかもしれませんが、「この研究が面白い!」と感じてくださった人が一人でも多ければ嬉しい限りです。
本記事を最後までお読みいただきありがとうございました!
9. 謝辞
本研究は、第63回 日本学生科学賞 情報・技術分野に応募し、入選三等を獲得することができました。また、第4回 東京学芸大学主催 SSH/SGH/WWL 課題研究成果発表会で発表を行い、口頭発表 SSH部門最優秀賞・ポスター発表 SSH部門優秀賞をダブル受賞しました。本研究に対して的確な助言をくださった担当教員の先生方に、感謝の意を表します。
また、本研究は、12月13日に行われた台湾生徒との研究交流会で発表されました。その頃の研究は 3 章の複雑な道路網で終わっていたのですが、そこで多くの批判とアドバイスを受け、それがきっかけとなって今日には 7 章まで研究が拡張されました。発表の機会をくださった先生方に、感謝の意を表します。
そして、本研究に関わったすべての方々に、改めて感謝の意を表します。本当にありがとうございました。
10. 参考文献
これらは、本研究において参考になった文献・サイトの中で、代表的なものです。
[1]
Introduction to Hill Climbing | Artificial Intelligence、GeeksForGeeks
山登り法の説明です。
[2]
Mirka Miller・Jozef Sirán、Moore Graphs and Beyond: A survey of the Degree/Diameter Problem、The Electronic Journal of Combinatrics、pp.5 - pp.15
先行研究とまでは行かないですが、本研究のきっかけとなった問題です。
[3]
秋葉拓哉・岩田陽一・北川宜稔、プログラミングコンテストチャレンジブック第2版、株式会社マイナビ、2013、pp.86-96
ダイクストラ法など、本記事で利用したアルゴリズムがたくさん書かれている本です。
[4]
John Cheng・Max Grossman・Ty McKercher、CUDA C プロフェッショナルプログラ
ミング、株式会社インプレス、2018、pp.2-8
スーパーコンピューター用のプログラミング言語「CUDA」でどうプログラムを書けば良いかが書かれています。
[5]
グラフと木(講義資料)
グラフ理論の考え方に基づいて研究が行われました。そのグラフ理論が解説されたPDFです。
-
30,000 回と書かれておりますが、これは高速化前のものであり、実際に 6 章で最短距離計算を高速化した後のソースコードでは 200,000 回のループを回しています。 ↩
-
道路網にほんの数個の変更があっても全体的な性質・傾向がほぼ変わらないことを利用しました。具体的には、変更の候補を 4096 個選び、「現在の道路網 $G$ から各変更だけを行った場合に最短距離合計値がどれほど短くなるか」を並列化計算で一気に計算し、その上位 64 個について、1位、2位、…64位という順に「道路網に変更を行い、悪化しなければそれを採用する」という操作を行うというアルゴリズムです。 ↩
-
簡潔に書くと、すべての道路の長さが 1 以上であり、かつほとんどのケースにおいて最短距離の最大値が $2N$ 以下である道路網の性質を使っています。頂点数が $N^2$ なので、ベルマンフォード法では本来 $N^2-1$ 回全辺を緩める必要がありますが、前述の性質を利用すると $2N$ 回しか緩める必要が無いことが分かります。そのため、計算量は $O(N^5)$ となります。 ↩
-
3 章の場合と同様、並列化に対応するため、道路網にほんの数個の変更があっても全体的な性質・傾向がほぼ変わらないことを利用しました。変更の候補を 4096 個選び、それぞれの変更を行った場合の最短距離合計値を求め、1位から64位まで順に変更を行うところまでは 3 章と同じで、そこからは「採用された変更の個数が64個中1個以内である場合、50%の確率で少し解が悪くなるような変更を行う」というアルゴリズムです。 ↩