0. はじめに --- 三角関数について思うこと
三角関数というと高校時代に苦しだ方も多いかもしれません。とにかく公式も多くて、最初のうちは何に使えるのかよくわからない印象を抱きがちです。しかし実際は、理系であればいかなる分野に進んでも、その分野の基本的な事象やツールが三角関数を用いて記述されています。つまり
- 高校のうちは三角関数が何に使えるのかよくわからず、よく理解せずに卒業して
- 大学や社会に入ってから三角関数を当然のように使うことになり、基礎から学び直すことになって大変な思いをする
という方が多いという話をよく聞きます。このような悪循環を断ち切るためにも、三角比・三角関数を学び始めた段階で「三角関数が何に使えるのか」を色々知っておくと、学びのモチベーションが高まるのではないかと思います。そこで本記事では、三角関数の使いどころについて特集してみます。特に、
- ゲームプログラミングなどで三角関数が必要になったけど、よくわかっていないので勉強したい
- 三角関数を勉強してみて、直角三角形に関する問題を解いたり、$\sin{x} = \frac{\sqrt{3}}{2}$ を満たす $x$ を求めたりなどはできるようになったけど、何に使えるのかピンと来ていない
といった方々に向けて、モヤモヤ感を少しでも晴らせるようなメッセージが届けられたならば、とても嬉しく思います。
1. 三角関数の使い方の overview
三角関数はありとあらゆる分野において、基本的なツールとして根付いています。音声処理において基本的な道具であるフーリエ解析は、そのベース部分で三角関数が使われていますし、ゲームプログラミングでは方向や回転を表すものとして三角関数が盛んに用いられます。三角関数の使われ方を整理すると、こんな感じだと思います。
| 使われ方 | 具体的な場面 |
|---|---|
| 測量 | GPS、地図、土木工学、精密機械工学、ケーキカット |
| 回転 | ゲームプログラミング、CG、航法、機械工学、宇宙機や航空機の姿勢制御 |
| 波 | 音声処理、画像処理、ノイズフィルター、振動工学、量子力学などさまざまな物理学分野 |
| その他1 | 内積、コサイン類似度、ボックス=ミュラー法(正規乱数の生成)、カーネル法における非線形関数としてなど |
「他にこんなのがある」というのがあったら是非いっぱい教えてください!
歴史的に最も古くからある用途は「測量」でしょう。三角関数誕生のキッカケはまさに測量の必要性にありました。比較的日常生活でも見る機会がありそうな用途でしょうか。
現代では「波」としての用途が多いでしょうか。Twitter での様々な人のコメントを見ていても、
といった具合に、波に関する話がかなり多いイメージです。これらの三角関数の使われ方を特集してみます。様々な分野に共通する三角関数の使い方のエッセンスを抽出したつもりですが、これでもかなり分量が多くなりました。摘み食いするような感覚で読んでいただけたら幸いです。
2. 三角関数の 3 つの顔
最初に三角関数には大きく 3 つの定義があったことを振り返っておきます。以下の記事にとてもよくまとまっています。
- 三角関数の3通りの定義とメリットデメリット (高校数学の美しい物語さん)
具体的には以下の 3 つの定義になります:
- 直角三角形による定義 ($90$ 度までしか扱えない)
- 単位円による定義 ($235$ 度とか $-15$ 度とかも扱えるように)
- マクローリン展開による定義 (角度部分が複素数でも扱えるように)
本記事の内容は基本的には、直角三角形・単位円までの理解で大丈夫です。
3. 測量
まずは最も古典的な測量方面での三角関数使用例を見てみます。これは三角関数を学ぶときに最初に教わる
直角三角形の三辺の比
としての三角関数をメインに意識した応用例たちです。なお三角関数の歴史について関心のある方は「三角法の歴史」を読むと面白いです。
3-1. 傾きを知る: 「長さ」から「角度」
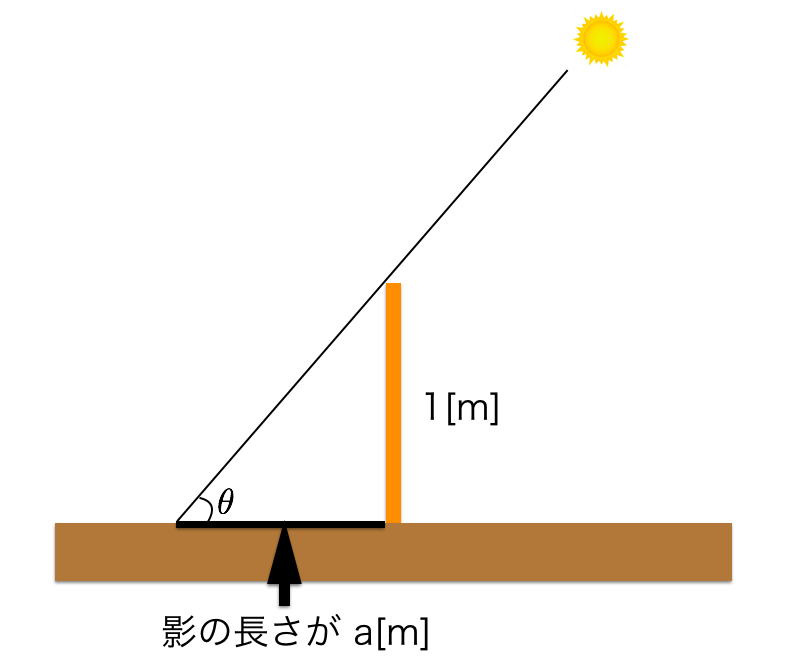
例えば、影の長さから太陽の高度 (角度) を測るのは、古くからある三角関数の利用方法の一つでした。太陽の高度を測ることは、日照時間や日の出時刻などとの関係が深くて重要でした。まだ $\sin, \cos, \tan$ といった記法のなかった古代から、このような用途で三角比が利用されていたのです。
下図のような太陽の角度 $\theta$ を求めたいとします。ここで例えば長さ $1$ m の木の棒を用意して影の長さが $a$ m だったとします。このとき、三角比の関係から、
$$\tan{\theta} = \frac{1}{a}$$
となります。$\frac{1}{a}$ の値は計算できるので、それを用いて角度 $\theta$ の値を逆算することができます。古代ギリシャ文明などではこのようなことをパッとできるように「三角法の数表」を作成していました。ヒッパルコスはそれによって月までの距離を大まかに求めていたとも伝えられています。
他の応用例
棒の影の長さから太陽の角度を求めるなんてのは、古代ならではの話であって現代の我々にはほとんど関係ないかもしれません。しかし数学のすごいところは、その考え方が色んなところに応用できることです。今回の肝は「長さと長さの関係から角度が計算できる」というところにあります。
- 震災時に家の傾きを求めた
- ゲーム作るために三角関数を勉強 (atan2 を紐解いています)
- CreateJS で三角関数を活用しよう
などなど、色んな場面で使います。特にゲーム制作においては、
向かっている目標物が、$x$ 座標方向に dx、$y$ 座標方向に dy 進んだ位置にあるとき、そこへ向かう角度は atan2(dy, dx) で求められる2。
というのは頻出の処理でしょう。この処理でやっていることは「棒と影の長さから角度を計算する」とほとんど一緒です。三角関数をよく理解していなかったがために atan2 で躓く方は後を絶たないと聞くので、基礎はとても大事ですね。
3-2. 距離を測る: 「角度」から「長さ」
前節は「長さの比」から「角度」を求める方法でした。今度は逆に「角度」から「長さ」を求める応用を見てみます。
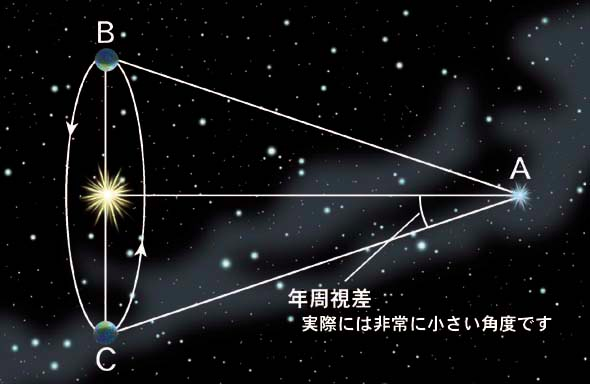
典型的な応用例として、地球から遠く離れた星までの距離を測る方法を取り上げてみます。色んな方法があるのですが、比較的近い星であれば年周視差を用いた方法が有効です。下図はこのページから引用しています。
図で、B と C との間で光り輝いているのが太陽で、B や C にいるのが地球です。地球は一年かけて太陽の周りをまわっているので、B の位置にいるときもあれば C の位置にいるときもあります。そして地球から A の位置にある星までの距離 (AB や AC の長さです) を測りたいです!
すごく賢いことに、
- 地球が B の位置にいるとき
- 地球が C の位置にいるとき
とで A の位置にある星の見える角度が僅かに変化します。この僅かな角度を測定します。図に整理すると以下のようになるでしょう。
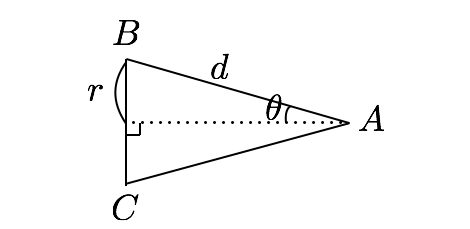
この図で
- 太陽から地球までの距離 $r$
- 年周視差を表す角度 $\theta$
はわかっている値です。これを用いて図の長さ $d$ を求めたいです。三角比の関係から
$$\sin{\theta} = \frac{r}{d}$$
となるので、これを $d$ について解くと
$$d = \frac{r}{\sin{\theta}}$$
と求めることができます。
他の応用例
以上のような方法には三角測量という名前がついていて、
と多彩な応用があります。測量はもちろんのこと、ステレオカメラも典型的な応用例です。また最後の、まだ地球が丸いことすら定説になっていなかった古代において、地球の大きさを測るためにエラトスネテスがとった方法は、とても面白いので是非読んでみてください。
3-3. 直角三角形以外では
ここまでの話題は、直角三角形に関する話でした。直角三角形以外の一般的な三角形に対しても、三角関数を有効活用したいです。
そこで登場するのが
- 正弦定理 $\frac{a}{\sin{A}} = \frac{b}{\sin{B}} = \frac{c}{\sin{C}} = 2R$
- 余弦定理 $a^2 = b^2 + c^2 - 2bc\cos{A}$
- 三角形の面積の公式 $S = \frac{1}{2}ab\sin{C} = \frac{1}{2}bc\sin{A} = \frac{1}{2}ca\sin{B}$
たちですね。これらは習得するのがしんどく感じる方も多いかもしれないですが、三角関数の有効範囲を拡げるためには重要なものです。その意識を持って学ぶと理解が深まるのではないかと思います。CG や、メッシュ分割を用いた構造解析など、一般的な三角形の幾何学を有効活用する場面も多いです。
4. 回転
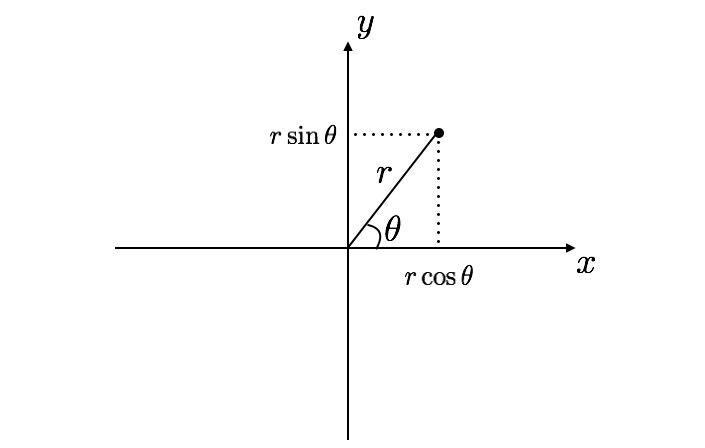
測量と似ているのですが、特に「回転」を表す応用の重要性から、回転に関する話題を集めてみます。「3. 測量」では直角三角形の辺の比を表すものとして三角関数をとらえましたが、今回は単位円で考えてみます。
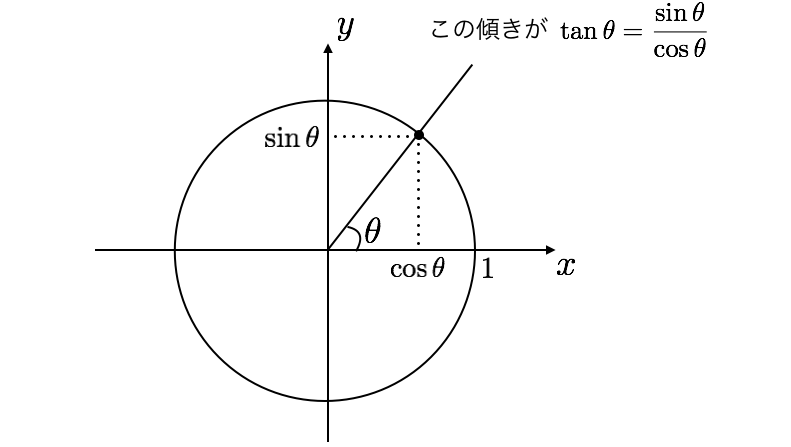
- 角度 $\theta$ に対して、
- 半径 $1$ の円 (単位円と呼びます) を考えて、
- $x$ 軸方向から $\theta$ だけ回転させた半直線を引き
- それと円との交点の $x$ 座標を $\cos{\theta}$、$y$ 座標を $\sin{\theta}$ とする
という風にして、三角関数 $\sin{\theta}$ と $\cos{\theta}$ を定義します。また $\tan{\theta}$ は
$$\tan{\theta} = \frac{\sin{\theta}}{\cos{\theta}}$$
と定義します。これは「半直線の傾き」を表しています。
4-1. 角度から向きを知る
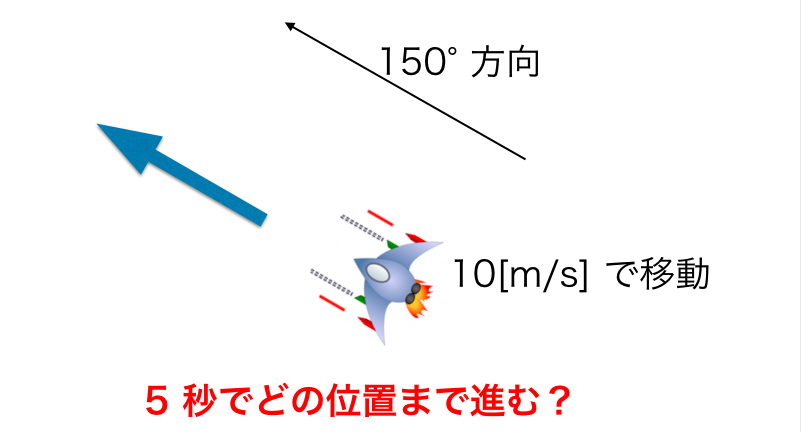
ゲーム制作や航法などにおいては、
「$x$ 軸方向からみて $150$ 度の角度方向に、秒速 $10$ m で進んだら $5$ 秒後にはどこにいるでしょうか」
といった問題にはしばしば遭遇します。
このような問題を解決する手段として三角関数は大変有効です。上の問題では結局 $10 × 5 = 50$ m 進んでいるわけですが、まずは $1$ m 進んだ場合にどこにいるのかを考えてみましょう。それを $50$ 倍すればいいです。
そこで単位円による三角関数の定義が大活躍します。ずばり
$$(\cos{150°}, \sin{150°}) = (-\frac{\sqrt{3}}{2}, \frac{1}{2})$$
の方向ですね。これを $50$ 倍して、求める座標は
$$(-25\sqrt{3}, 25) \fallingdotseq (- 43.3, 25)$$
になります。このように $(\cos{\theta}, \sin{\theta})$ というのは、角度 $\theta$ の向きを表すベクトルであると言えます。
こぼれ話
三角関数不要論に伴い「斜め $45$ 度方向に進むと移動速度が $\sqrt{2}$ 倍になるゲーム」が話題になりました。
- $x$ 軸方向に進むと $1$ 秒に $(1, 0)$ だけ進む
- $y$ 軸方向に進むと $1$ 秒に $(0, 1)$ だけ進む
- 斜め $45$ 度方向に進むと $1$ 秒に $(1, 1)$ だけ進む
という風にしてしまった影響のようです。実際、$(1, 1)$ の移動距離を計算すると $\sqrt{1^2 + 1^2} = \sqrt{2}$ となります。もし斜め $45$ 度方向に進んでも「秒速 $1$」を保ちたければ $1$ 秒に
$$(\cos{45°}, \sin{45°}) = (\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})$$
進むとすればよいです。一般に角度 $\theta$ 方向に進んで秒速 $1$ を保つには、$1$ 秒に $(\cos{\theta}, \sin{\theta})$ 進むとすればよいです。
他の応用例
三角関数のこの使い方は、極めて多くの分野で使用されているアイディアなので、応用例を挙げるのはキリがないですが、すごく面白いものを並べてみます!4-3 で紹介する「回転」を使うものも含めています。
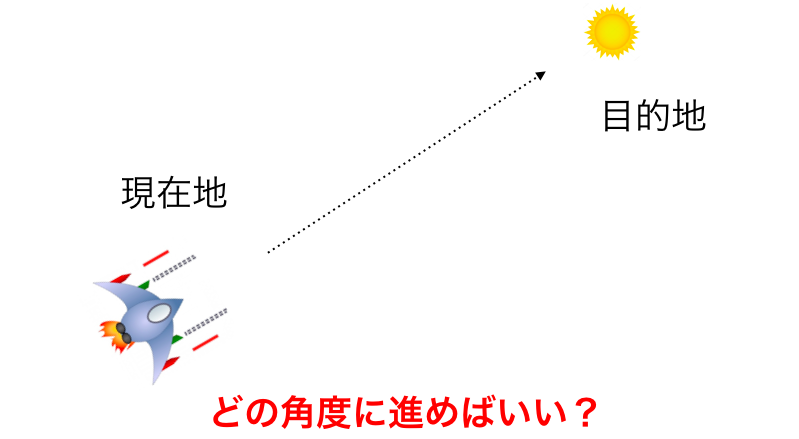
4-2. 向きから角度を知る: atan2
前節は「角度から向きを知る」という方向性の話でしたが、今度は「向きから角度を知る」という方向の話です。3-1. 傾きを知る --- 「長さ」から「角度」でも紹介した話なのですが、atan2 に関する話になります。
角度 $\theta$ 方向に距離 $d$ だけ進むと、$(\cos{\theta}, \sin{\theta})$ を $d$ 倍して
$$(d\cos{\theta}, d\sin{\theta})$$
だけ進むのでした。反対に
$$(x, y)$$
だけ進もうとしたときに、その方向の角度を知りたい場面も多々あります。それを実現できるのが atan2 関数です。そのようなことをしたい場面としては
- 航法において、目的地方向へと進みたい
- 天体観測において、望遠鏡を所望の星へと向けたい
- ゲームプログラミングにおいて、目標物にカメラを向けたい
といったものがあります。
4-3. 二次元の回転
単位円周上の点を $(\cos{\theta}, \sin{\theta})$ ($x$ 軸とのなす角が $\theta$) と表したわけですが、これをさらに複素平面上の点とみなして
$$\cos{\theta} + i\sin{\theta}$$
と表すことにすると、さらに豊かな世界が広がります。もっと一般に複素数 $x + yi$ に対し
- 原点からの距離が $r$
- $x$ 軸方向とのなす角度が $\theta$
となっているとき
$$x + yi = r(\cos{\theta} + i\sin{\theta})$$
と表すことができます。
そして複素数は単に「複素平面上の点」を表すだけでなく
複素平面上の点に複素数 $\cos{\theta} + i\sin{\theta}$ をかけ算することは、原点周りに角度 $\theta$ だけ回転させる操作を表す
という「回転操作」をも表しています。このように少し踏み込んで考えてみると面白い世界が見えて来ます。例えば「角度 $\beta$」を表す点 $\cos{\beta} + i\sin{\beta}$ に対して角度 $\alpha$ だけ回転させた点は
(\cos{\alpha} + i\sin{\alpha})(\cos{\beta} + i\sin{\beta}) \\
= (\cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}) + i(\sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta})
となります。そしてよく考えるとこれは
$$\cos(\alpha + \beta) + i\sin(\alpha + \beta)$$
と一致しているはずです (角度 $\beta$ に $\alpha$ だけ回転させると角度 $\alpha + \beta$ になります)。両者を比べると三角関数の加法定理が導かれたりします:
- $\cos(\alpha + \beta) = \cos{\alpha}\cos{\beta} - \sin{\alpha}\sin{\beta}$
- $\sin(\alpha + \beta) = \sin{\alpha}\cos{\beta} + \cos{\alpha}\sin{\beta}$
なお関連する話として、オイラーの公式としてよく知られているのは
$$e^{i\theta} = \cos{\theta} + i\sin{\theta}$$
という式ですね。これによって角度 $\theta$ だけ回転させる操作が $e^{i\theta}$ と非常にシンプルに表すことができるようになりました。交流回路などを解析したり、フーリエ解析したりするときに、とてもやりやすくなります。
応用例
三角関数の回転を使うと、純粋に見ているだけで楽しくなるようなアートが沢山作れます!
アートとしてだけでなくリサジュー図形といった応用もあります。そのあたりの話は以下の記事が大変面白いです:
4-4. 三次元の回転
ここまで「角度」や「回転」に関する話をしたのですが、二次元空間を前提とした話になっていました。現実には、
- 3D ゲームプログラミング
- 3D コンピュータグラフィックス
- 航空機や宇宙機の回転や姿勢
などなど、三次元物体の回転や姿勢を表したい場面も多々あります。三次元物体の回転や姿勢を表すにはクォータニオンやオイラー角を用いる方法があります。三次元の回転が扱えるようになると、応用範囲がグッと広がりますね。二次元と同様、三角関数を使いまくります。三次元回転については以下の記事にまとめたので是非読んでいただけたらと思います。
5. 波: フーリエ変換
最後に比較的高度な話題になりますが、多くの方にとって三角関数を必須のツールたらしめている「波」という見方についてです。三角関数は「波」を表す基本的な道具として、理系のあらゆる分野で広く根付いています。その思想の一端を紹介できればと思います。
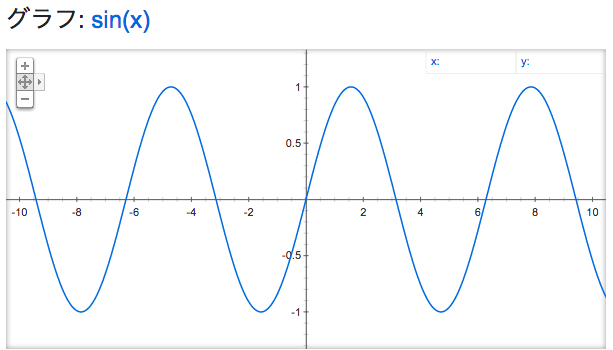
いきなり波だと言われても、「直角三角形の比」がどう波とつながるんだと疑問に抱く方も多いかもしれません。しかし試しに $y = \sin{x}$ のグラフを描いてみると「確かに波っぽいな」という気持ちになります。
このように、$\sin, \cos, \tan$ を単なる三角比を表すものだという認識を超えて、$f(x) = \sin{x}$ という三角関数を考え始めることで、ものすごく豊かな世界が眼前に広がって行きます。
5-1. 単振動
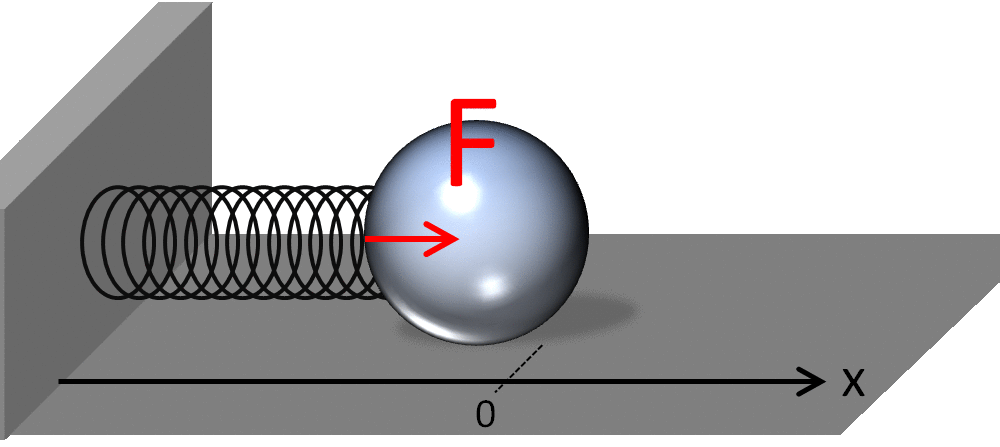
まずはこの三角関数のもつ「波っぽさ」を見つめてみたいと思います。以下の画像は wikipedia からの引用です。
バネが左右に振動していますが、この振動は実は三角関数を用いて表すことができます。バネの先端のボールの動きは、時刻 $t$ に対して
$$x = d\sin{\omega t}$$
という風に表せます。このような振動を単振動と呼びます。そしてこの動画を見ると、
- 円周上の等速運動
- バネの単振動
- サインカーブ
が有機的につながっていることが見てとれます。さて、理想化されたモデルにおいて単振動で記述される振動の例としては
- バネ
- 振り子
- 電気回路
- 音 (空気の振動)
などが挙げられます。私たちは「振動」という言葉からバネや地震などを連想しがちですが、電気回路や信号処理、音声処理も扱えることを認識すると、三角関数の応用範囲が爆発的に広がります。株価のような時系列データもそのような扱いをすることで有益な情報を引き出せることも多いです。さらに、画像のような離散的な対象に対しても「周波数成分を取り出す」という営みが拡張されていて、JPEG 圧縮技術や、多倍長整数計算などにも応用されています。
5-2. もっと複雑な振動も
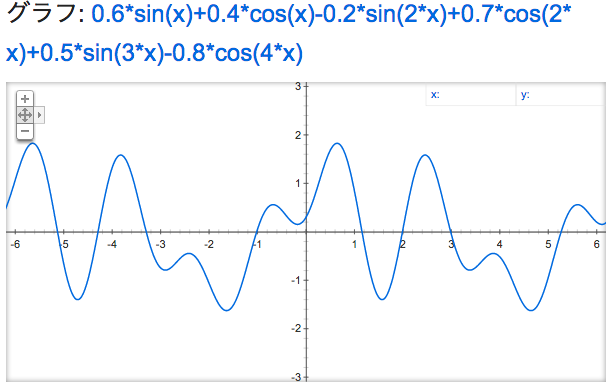
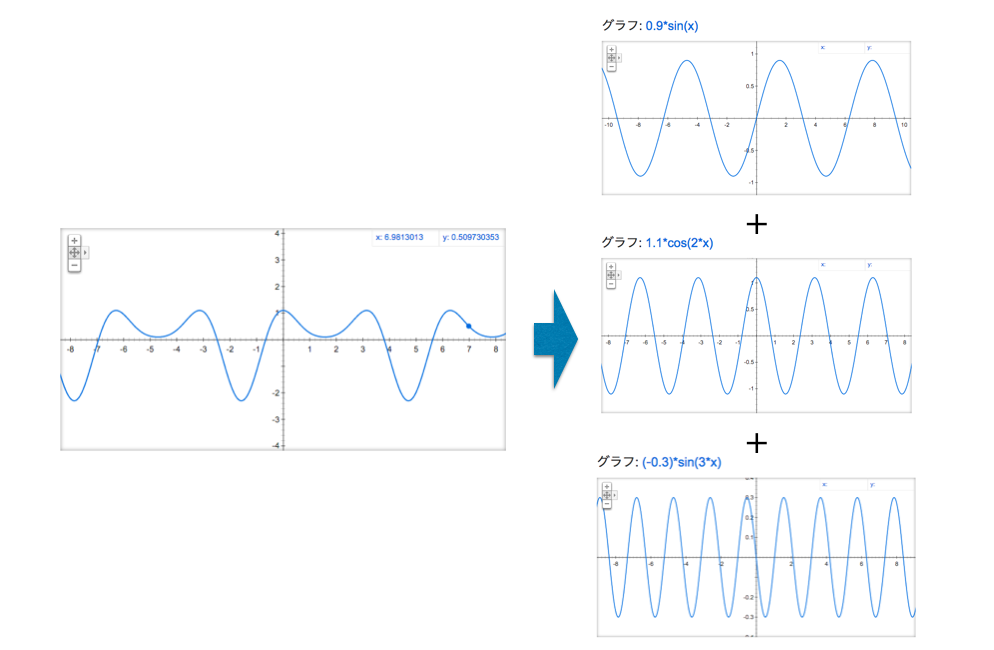
前節で登場した単振動は、最も単純な振動だと言えます。しかしすごいことに、三角関数を組み合わせるとかなり複雑な振動を表現することができます。例えば下図のようなかなり複雑な波形も三角関数の重ね合わせで表現できます。
そして驚くべきことに、$0 \le x \le 2\pi$ の範囲で定義された連続関数 $f(x)$ は、(厳密には、区分的に滑らかで周期 $2\pi$ の周期関数であれば) どんなものであっても、
$$f(x) = c + a_1 \cos{x} + b_1 \sin{x} + a_2 \cos{2x} + b_2 \sin{2x} + a_3 \cos{3x} + b_3 \sin{3x} + \dots$$
という形で書けることが数学的に示されています3!!!!!
歴史的には 19 世紀はじめに、フランスの数学者・物理学者フーリエが「熱の拡散を表す拡散方程式」の解を求めようとして生み出したアイディアであるようです。その話は
に詳しく書かれています。とても面白いです。誤解を恐れずにいえば、
ありとあらゆる振動・波動現象は、三角関数の重ね合わせとして理解できる
ということになります!!!!!
具体的に上式の $c, a_1, b_1, a_2, b_2, \dots$ を求める方法については、実は意外とすごく簡単で、
- $\sin{nx}$ の係数 $a_n$ を知りたかったら、$f(x)$ に $\sin{nx}$ をかけて積分する ($a_n$ 以外の項は消える)
- $\cos{nx}$ の係数 $b_n$ を知りたかったら、$f(x)$ に $\cos{nx}$ をかけて積分する ($b_n$ 以外の項は消える)
だけで求めることができます。なぜこんなに単純に上手く行くかの背景については、この記事に明快に記されています。
5-3. フーリエ変換の使い道
フーリエ変換とは、ここではざっくり、関数 $f(x)$ に対して上述の $c, a_1, b_1, a_2, b_2, \dots$ を求める操作のことだと思うことにします。そしてフーリエ変換の使い道については、以下の資料たちにとてもよくまとまっているので是非読んでみると面白いです。
これらをまとめると、フーリエ変換の御利益として以下の 3 つが挙げられるでしょう:
- 関数にどんな周波数成分が含まれているかが分かる (スペクトル分解)
- 微分方程式を解くのに使える (フーリエ自身のモチベーションもこれでした、現代では気象予報のための数値シミュレーションなどに実際に用いられています)
- 畳み込み計算に使える (信号処理や制御工学に応用多数、高速な円周率計算などへの応用も)
ここでは 1 番目のスペクトル分解に関するメリットについて簡単に掘り下げてみたいと思います。
5-4. 三角関数の周波数について
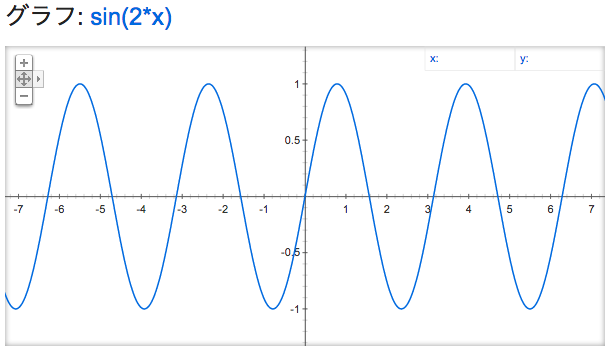
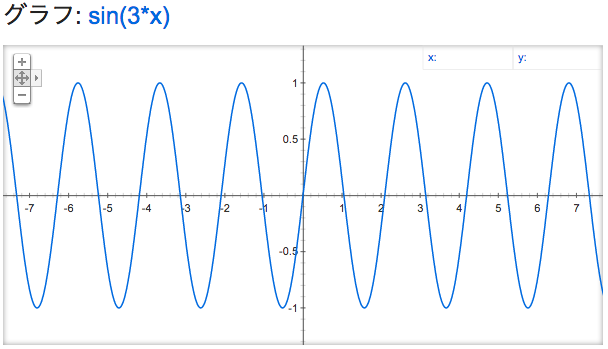
フーリエ変換のメリットについて掘り下げる前に、三角関数の周波数についておさらいしてみます。早速ですが、$\sin{x}$, $\sin{2x}$, $\sin{3x}$ のグラフを上から順に並べてみます:
徐々に揺れの周期が短くなっていることがわかります。一般に
- 三角関数 $y = \sin{\omega x}$ や $y = \cos{\omega x}$ において、$\omega$ を角周波数と呼ぶ
のでした。角周波数の意味は、
- 角周波数が $1$ のとき、$x$ が $2\pi$ 変化するごとに $1$ 周する (つまり周期は $2\pi$)
- 角周波数が $2$ のとき、$x$ が $2\pi$ 変化するごとに $2$ 周する (つまり周期は $\pi$)
- 角周波数が $3$ のとき、$x$ が $2\pi$ 変化するごとに $3$ 周する (つまり周期は $\frac{2\pi}{3}$)
- ...
という感じです。そして異なる周波数の三角関数を
$$y = 0.3 + 0.1\sin{x} - 0.7\cos{x} + 0.4\sin{2x} - 0.5\cos{3x} + 1.4\sin{4x} + 0.2\cos{4x} + \dots$$
という風に重ね合わせると、様々な複雑な波形を表せるようになります。フーリエ変換は逆に「波形が与えられて、それを角周波数ごとに分解する」というイメージです。
なお、具体的な振動において、角周波数がどのような意味をもつのかを整理してみます。これによってスペクトル分析の重要性が見えて来るのではないかと思います。
| 振動の種類 | 周波数のもつ意味 |
|---|---|
| バネ | 周波数が大きいほど、より高速に振動 |
| 振り子 | 周波数が大きいほど、より高速に振動 |
| 電気回路 | 周波数が大きいほど、より高速に位相が変化 |
| 音 | 周波数が大きいほど、より高い音 |
5-5. スペクトル分析
バネの振動や、建物の振動、地震といった力学的な振動から、電気回路・信号処理といった電気的な振動、音といった空気の振動、はたまた株価のような時系列データまで、世の中には振動としてと扱いたい現象がたくさんあります。画像でさえ、隣り合うセル間の離散的な振動とみなすことで JPEG 圧縮などの豊かな技術が生まれます。
このようなデータを分析する手段の一つとして、フーリエ変換してみるのは大変有力です。これにより、分析したいデータにおいてどの周波数成分が強いのかを分析することができます。そのような応用例としては、
-
地震波を分析することで、どの周波数成分が強いかがわかれば、その周波数の揺れに強い建物を作るなどの対策を打ちやすい
-
株価などを分析することで、1 年周期の周波数成分が強いことがわかれば、季節依存性が高いことが読みとれる
-
年周視差が計測できないような遠い銀河までの距離を知りたいときは、銀河の遠ざかって行くスピードを求めることで距離を推定するが、そのスピードを求めるために「遠ざかっている物体から出る光の波長は長い方にずれる」という性質 (赤方偏移) が利用できる4 (「宇宙の大規模構造」を参照)
-
カラオケ精密採点において、歌声をフーリエ解析することで、音程を推定することができる (ボーカロイドも似た使い方です)
などなど非常に多彩です。
5-6. 高周波成分 (ノイズ) の除去
分析したいデータのフーリエ変換に関する、さらなる典型的な応用として
高周波成分を除去する
という考え方があります。例えば $y = \sin{10000x}$ のグラフを見てみましょう。
もはや波として認識できるものではなさそうですね。実際例えば
といった状況になっています。このような高周波成分を除去してしまう考え方があります。それによって
といった効果を期待しています。JPEG 圧縮に関しては大変勉強になる資料があるので是非読んでみると面白いです!(下図はスライドからの引用です)
6. おわりに
三角関数の使い方として思い浮かんだものを並べてみました。これらによって、これから三角関数を学ぶ方のモチベーション向上に寄与できたり、三角関数の摑みどころのなさを感じていた方のモヤモヤを少しでも晴らしたりできたならば、とても嬉しい気持ちです。
7. 参考文献
三角関数周辺の数理について参考になりそうな資料たちです。
数学史
歴史的にどのようなニーズがあって三角比が誕生したのかを知ることは、大変有益だと思います。
三角関数の考え方や基本公式
三角関数周辺の話題について、基礎的なものからマニアックなものまで、大変コンパクトによくまとまっています。
大変わかりやすい三角関数の解説です。
とても丁寧で読みやすいです。三角関数に親しみを持てます。
フーリエ変換
フーリエ変換を初めて学ぶ本としていい感じです。
わかりやすいフーリエ変換に関する参考書です。