数学...ずっと避け続けてきたけど、どうしても乗り越えなければならない壁っぽいので、ちょっとずつ勉強。。
サンプル
import SpriteKit
class GameScene: SKScene {
var triangle: SKShapeNode!
override func didMoveToView(view: SKView) {
self.backgroundColor = UIColor.whiteColor()
//三角形を作る
let length: CGFloat = 100
var points = [CGPoint(x:length, y:-length / 2.0),
CGPoint(x:-length, y:-length / 2.0),
CGPoint(x: 0.0, y: length),
CGPoint(x:length, y:-length / 2.0)]
triangle = SKShapeNode(points: &points, count: UInt(points.count))
triangle.fillColor = UIColor.grayColor()
triangle.position = CGPointMake(self.frame.midX, 120)
self.addChild(triangle)
}
override func touchesBegan(touches: NSSet, withEvent event: UIEvent) {
for touch: AnyObject in touches {
let location = touch.locationInNode(self)
//triangleの位置
let trianglePosition = triangle.position
//traiangleの新しい角度
let radian = -atan2(location.x - trianglePosition.x, location.y - trianglePosition.y)
//回転アクション
let rotate = SKAction.rotateToAngle(radian, duration: 0.5)
//回転アクション実行
triangle.runAction(rotate)
}
}
ここがわからない所。
let radian = -atan2(location.x - trianglePosition.x, location.y - trianglePosition.y)
タップした座標と三角の座標の差をatan2すると、欲しい角度が得られるらしい。。
ググったところ、atanは「アークタンジェント」のことで、「タンジェントの逆三角関数」であるとのこと。辺の長さから角度を求めるために使われるものらしい。
確かに、角度を求めるために使われている...が、理屈が全くわからない。
タンジェントが三角関数だってのはさすがに知ってたので、三角関数について色々調べてみたんだけど
初心者のための三角関数講座
これが一番わかりやすかった。
どうやらアークタンジェントを理解するには、タンジェントの理解が必要で、タンジェントを理解するためには、サイン、コサインを理解する必要があるらしい。
以下学習した内容のまとめ。
まえおき
三角関数をより理解するためには、まず「円」と「直角三角形」の関係を理解しておくと良いとのこと。ただ、ここを飛ばしても(多分)大丈夫なので、割愛。詳しく知りたい場合は、こちらを
初心者のための三角関数講座~準備編Ⅰ~
初心者のための三角関数講座~準備編Ⅱ~
サイン(sin)、コサイン(cos)、タンジェント(tan)は何者?
・sin,cos = 斜辺に対して何倍の長さか。
・tan = sinのcosに対する比。傾きの大きさ。(後述)
(tanはsinとcosを使って算出するものだといことをここで初めて知った)
まず、sin,cosについて図にするとこうなる。

・斜辺 = 直角のところにくっついていない辺
・cos = 直角とθがくっついてる辺("隣辺"というらしい)
・sin = 直角とはくっついてるけど、θとはくっついてない辺("対辺"というらしい)
sin, cos = 斜辺に対して何倍の長さか、つまり、斜辺に対するする比を表しているので
仮に
斜辺 = 1
θ = 60°
とすると、こんな感じ
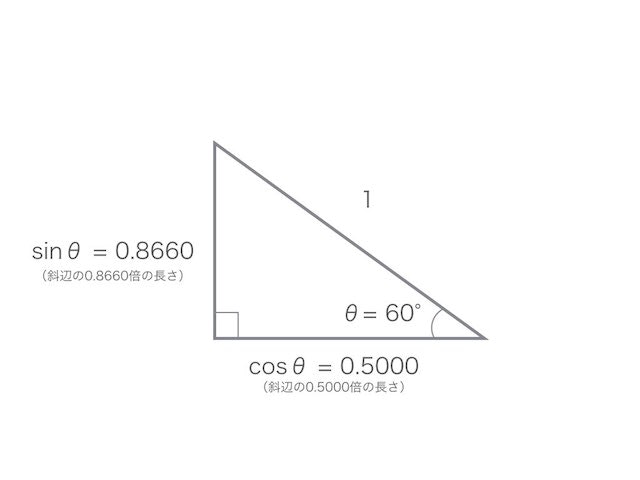
これを三角比といって、早見表なるものを見るとそれぞれのsin, cos, tanがわかる。
また、
斜辺 = L
とすると、こうなる。
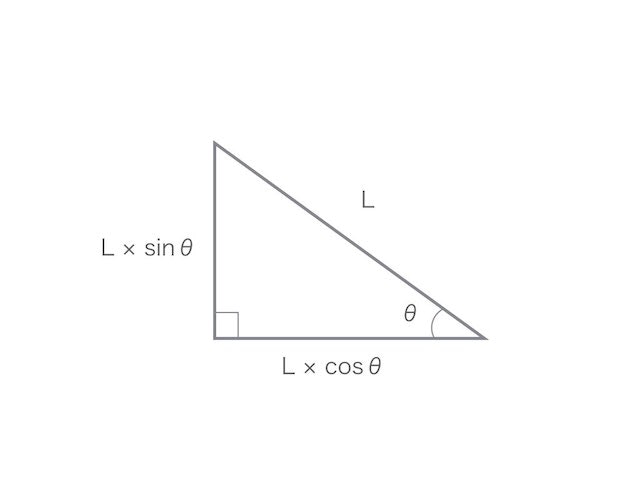
斜辺をLとした場合、
sinの辺の長さ = L × sinθ
cosの辺の長さ = L × cosθ
sinとcosが、斜辺に対して何倍の長さなのかを表すもの、というのがこれで理解できた。
tanについて
tanはsinのcosに対する比である(sinをcosで割った値)。つまり、tanは傾きの大きさを表している。
tanはsinとcosを使って計算するもので、tan = sin ÷ cosで算出される。
試しに
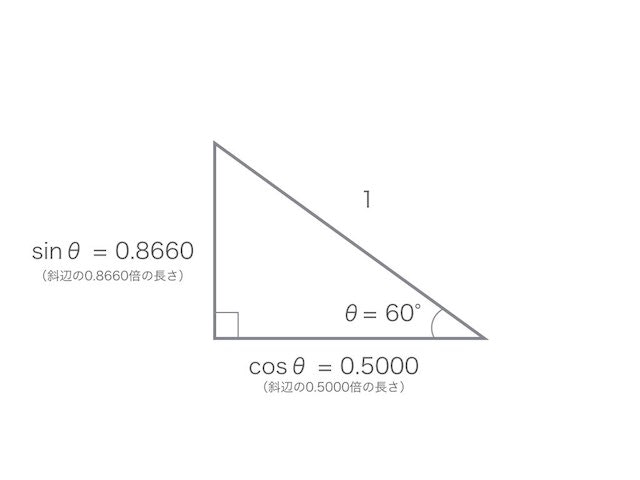
のtanを計算してみると
tan = 0.8660 ÷ 0.50000 = 1.732
早見表を見ても、その通りになっている。
しかし、まだsinのcosに対する比が何を意味するかわからない。というか、自分の学力では、"tanは傾きの大きさを表している"の"傾き"が、そもそも何だったか怪しかったので、そこから。
傾きについては、調べたらすぐ理解できた。(中学で習ったやつだった)
一次関数 y = ax のaが傾き
y = 2x だとこんな感じ。
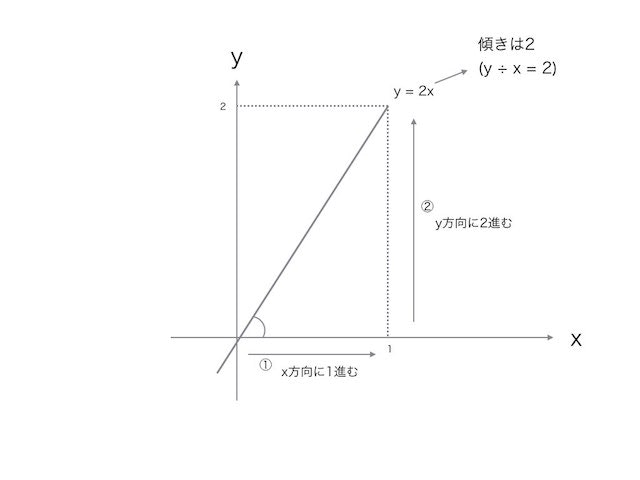
で、この図で一次関数の斜めの線と①と②で直角三角形が出来ているのがわかる。
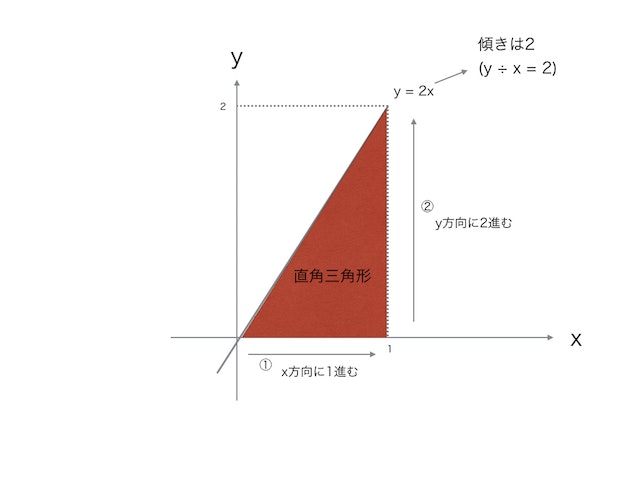
これにsin, cos, tanを当てはめると、
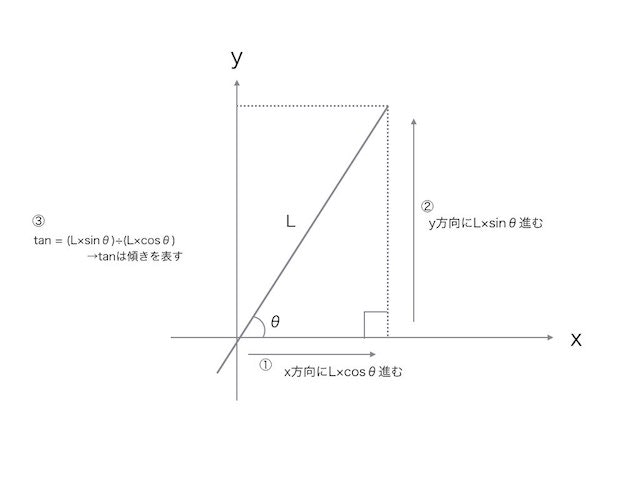
tan = sin ÷ cos なので
tanは傾きの大きさを表している、ということになる。
さっきみたいに
斜辺 = 1
θ = 60°
とすると、こんな感じになる。
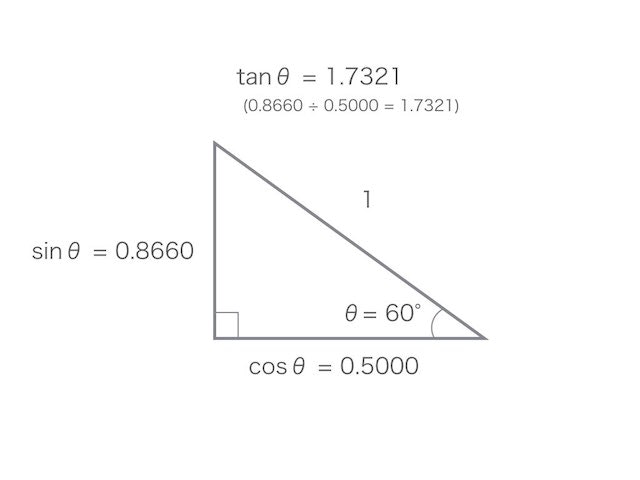
で、じゃあ具体的にtanをどう使うかというと、例えば
θとcosθがわかってて、sinθが変わらない場合
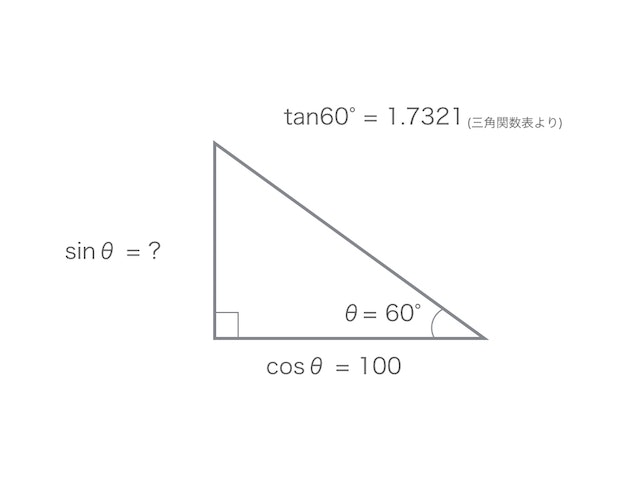
tan = sin ÷ cosだから
1.7321 = sin ÷ 100
sin = 173.21
と計算出来る。(tanは算出できないから、三角関数表を参照することになる)
もちろん、cosθが?の場合でも同じように算出できる。
これで、sin, cos, tanが何者かざっくりとわかった。
これでようやく、アークタンジェント(atan)へ進むことができる。
アークタンジェント(atan)とは?
結論から言うと
角度は分かるけど長さが分からない(長さの値を出したい)場合に使うのが tan で、長さは分かるけど角度が分からない(角度の値を出したい)場合に使うのが atanになる。
θ = 60°の場合、tan = 1.7321 となる。(三角比の表参照)
これと同じ直角三角形について、もし、辺の長さが分かっていて角度が分からないときは、こんな感じになる。
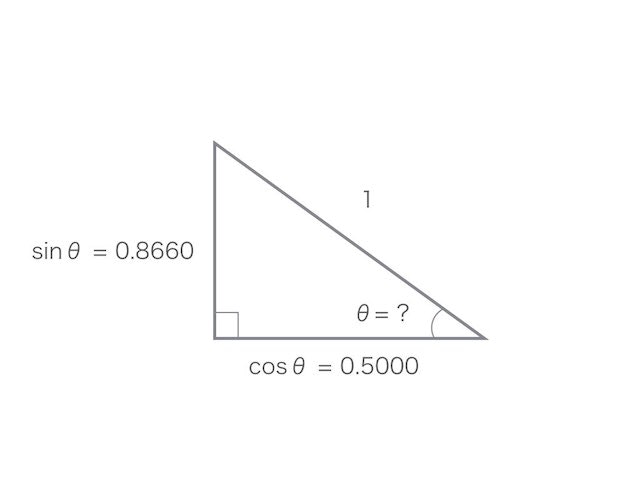
で、このθを求めたいときに atan を使う。
使い方は、atanにtan(= sin ÷ cos)を代入するだけでOKとのこと。
atan(sin ÷ cos) = θ
すなわち
atan(tan) = θ
この場合なら
atan(0.8660÷0.5000) = atan(1.732) = 60°
となり、こんな感じになる。
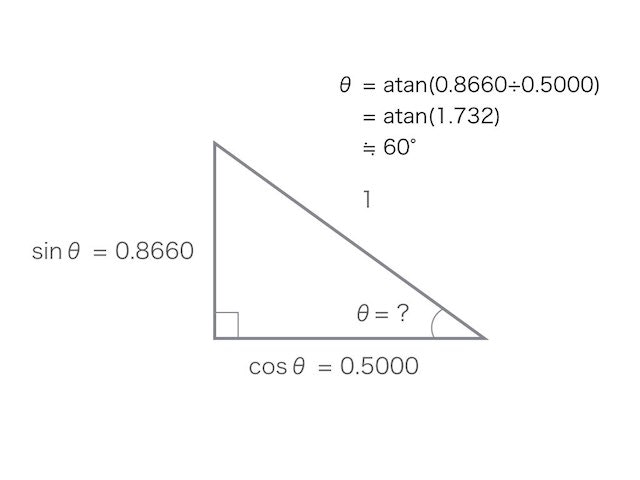
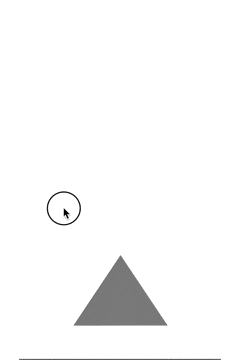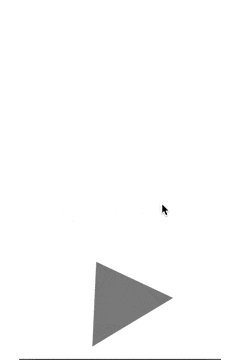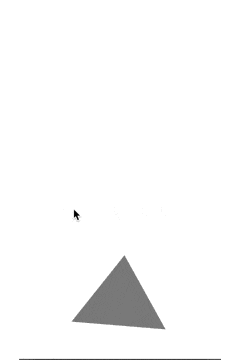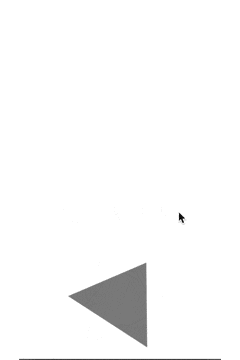
で、サンプルを思い出すと
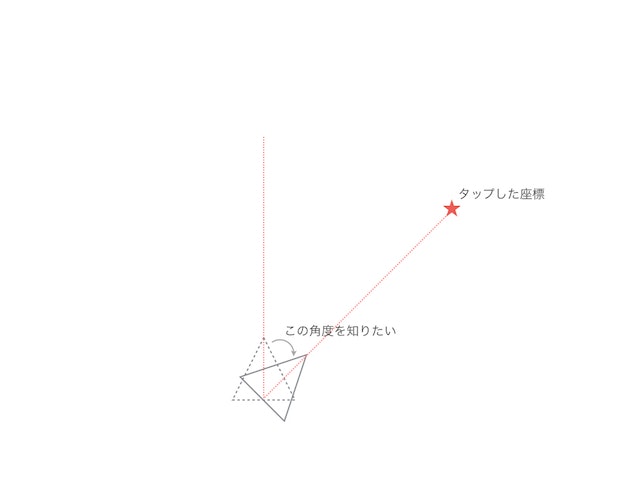
こんな感じだったんだけど
これに勉強したことを応用するとこんな感じになる。
①
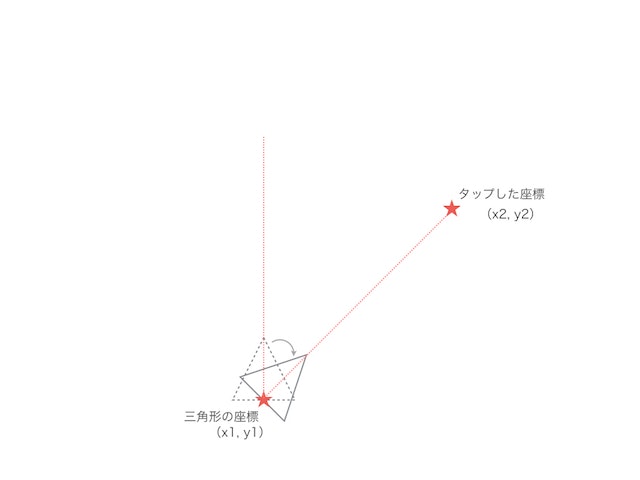
②
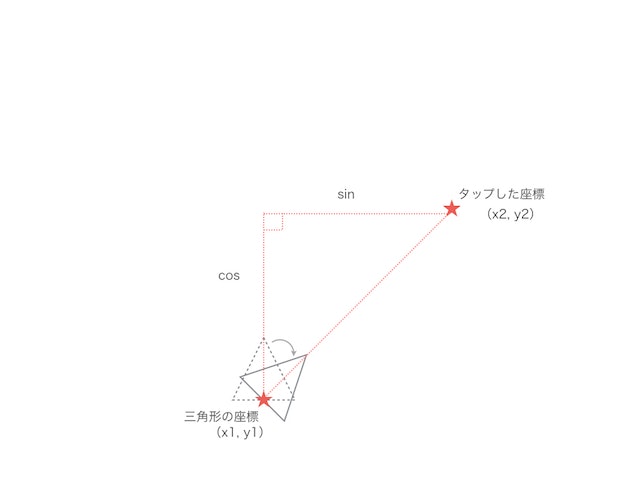
③
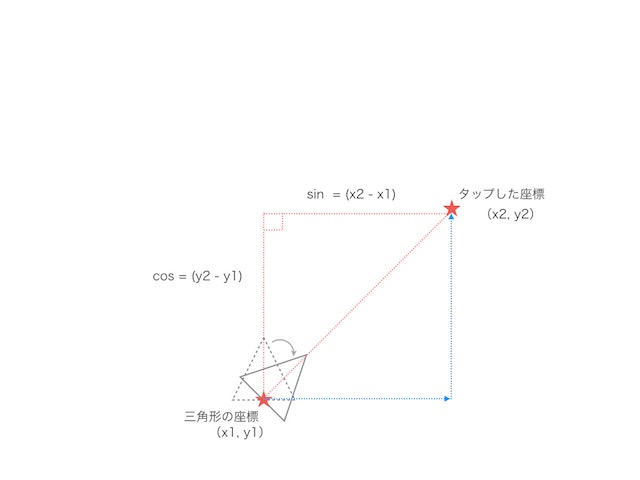
④
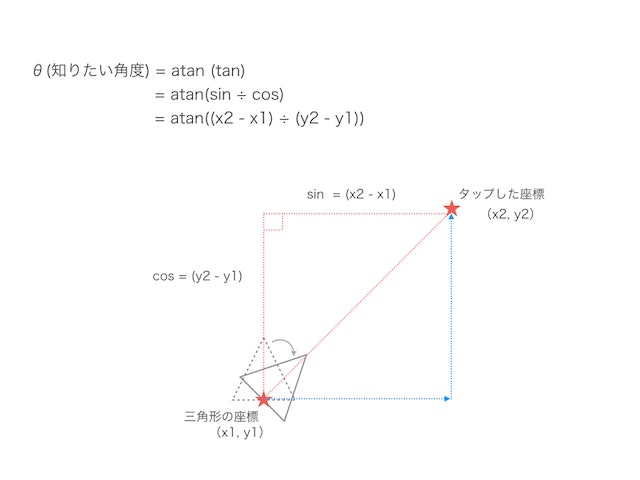
atanまでたどり着いた
let radian = -atan2(location.x - trianglePosition.x, location.y - trianglePosition.y)
を見てみると、atanの中にsinとcosが入っていて、欲しい角度が計算されていることがわかる。(swiftだとatan2って名前らしい。マイナスが付いてるけど、これがないとタップした方と逆向きに向くみたい...これはまたいつかどこかで調べよう)
さいご
お気づきかと思いますが、atanの計算の仕組みには全く触れてません。
どうやらこれを解析するには、テイラー展開とか、加法定理とか
そういうやつを使わなきゃいけないみたいで、とりあえず、自分には無理だということは理解しました。atanの使い方が理解できたので今回はOK