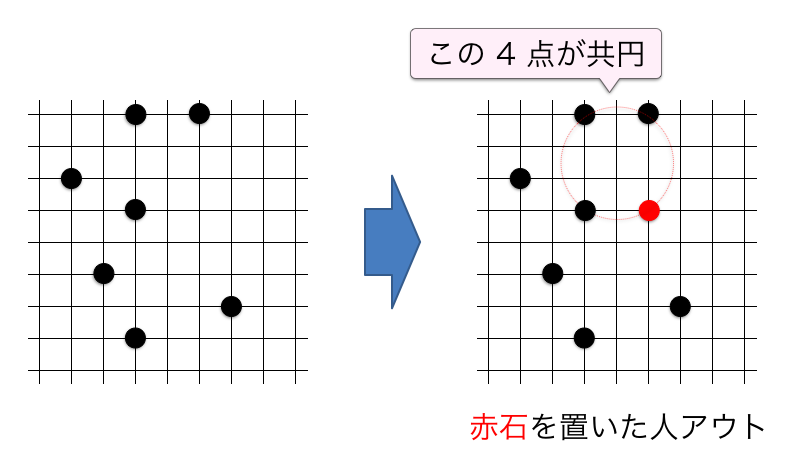
0. 共円 --- プログラマにオススメ...?
本記事は
プログラマーにオススメしたいゲーム紹介 Advent Calendar 2018
の 7 日目の記事として書きました。僕は 10 代後半の頃に超絶ハマった「共円」というボードゲームをオススメしたいと思います!
共円は囲碁や五目並べと同じく、格子点上に石を置いていくゲームに分類されるのですが、平たく言えば「2〜5 人が順番に格子点上に碁石を置いていく、ただし自分のも相手のも含めてどの 4 個の碁石も同一円周上にならないように置いていく」というものです。
いかにも素朴な数学が沢山詰まってそうで心そそられますね!!!!!
整数論はもちろんのこと、組合せ数学や初等幾何学の要素をふんだんに含んだ考察も楽しめる、高校数学好きな人にとってこの上なく魅力的なゲームだと思います。プログラマにオススメとは...
競技プログラマ的には、共円な問題が時々出題される...ような気がします。たぶん。。。でも実際、
(競技プログラミングに出題される問題たちの背景となる、様々な整数論のテクニックを集大成した資料です)
では、7 章で二次体の話が少し出て来ますし、11 章の単項イデアル整域ではガウス整数を用いて綺麗に解ける例題が紹介されています。AGC 025 D - Choosing Points もガウス整数のイメージを持っていると解きやすい問題でした。
このようにガウス整数をはじめとした整数論に触れておくことは、競技プログラミングにも役に立ちます。ガウス整数に限らず、応用が利くテクニックを色々学んでおくことは有益と言えるでしょう。僕自身もつい先日の企業合コン1で、某難問が「素因数分解界隈の人にとっては常套手段らしいテクニック」によって鮮やかに解かれていた場面を目撃しました。今回はガウス整数に焦点を当ててみます。「共円」はガウス整数を学ぶことのできる格好の題材です。
1. 共円とは
まずは共円というゲームを紹介しまくります!
共円のルールからはじまり、とても魅力的な共円定石たちを紹介して行きます。
1-1. 共円のルール
ルールはいたってシンプルです。
プレイヤー人数
2〜5 人
用意するもの
「格子」と「石」が必要ですが、様々なもので代用できます。また注意点として、オセロも囲碁も「白」「黒」の二色の碁石を使いますが、共円では一色でよいです。
| 代用品 | |
|---|---|
| 格子 | オセロ盤、囲碁盤、方眼紙、白紙に格子を書く、目隠し脳内プレイするなど2 |
| 石 | オセロ石、碁石、ペンで黒丸を書く、脳内に石を配置するなど |
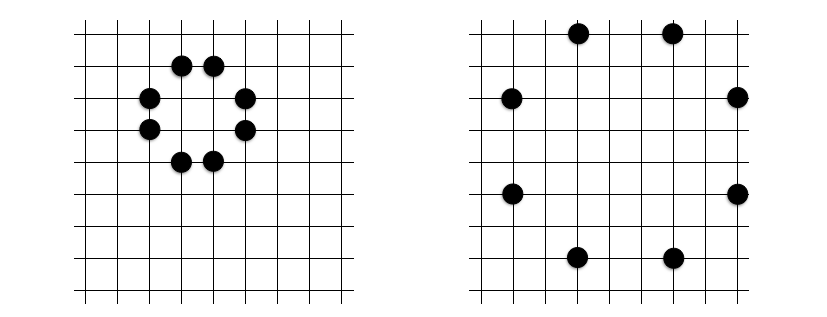
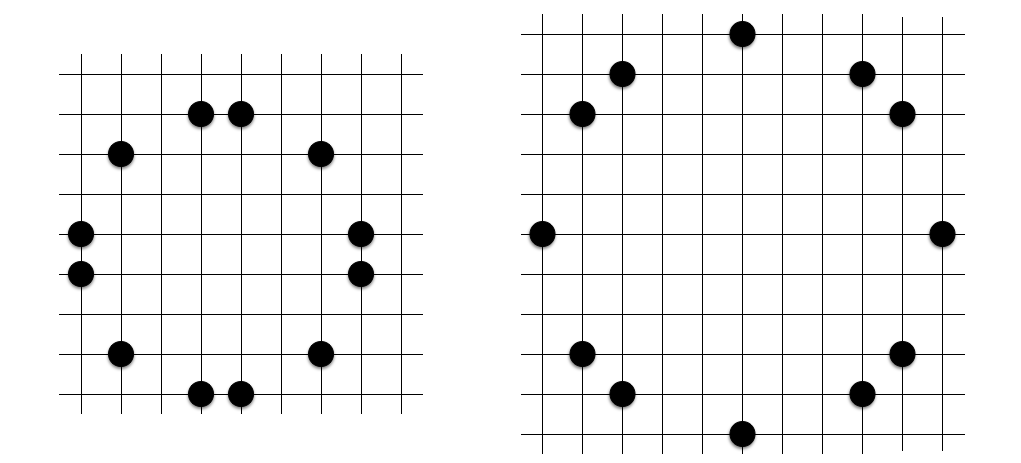
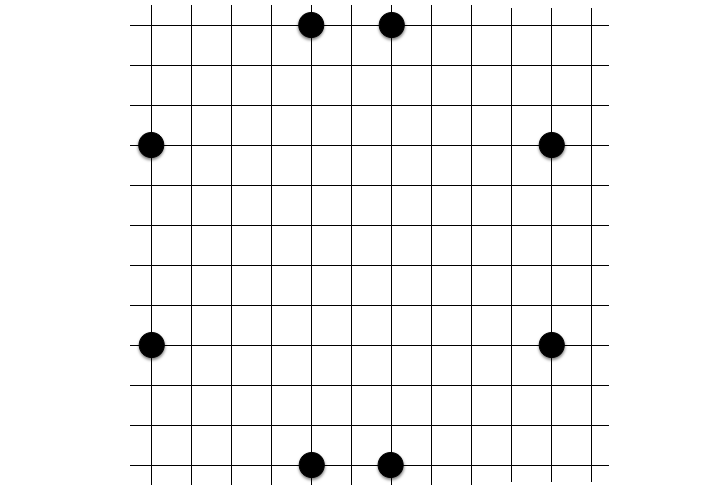
なお、実際に使用する格子は、「9 × 9 の九路盤」でプレイすることが多いです。オセロ盤を使うと下図のように自然に九路盤になります。
プレイの流れ
「同一円周上にある 4 石」または「4 石が同一円周上にある状態」を「共円」と呼ぶことにします。またルールとして「同一直線上にある 4 石も共円とみなす」ことにします。このとき、プレイの流れは以下の通りです:
- 一人ずつ順番に石を置いて行きます
- もしある人の置いた石を含む共円が発生したのを他の人が見つけた場合、見つけた人はそれを指摘することができます
- その指摘が正しい場合、指摘された人は脱落し、その石は盤面から取り除かれます
- 仮に実際は共円が発生していても、指摘される前に次の人が石を置いた場合はセーフです (時効)
- 最後に残ったプレイヤーの勝利です!
1-2. 詰共円: 共円のトレーニング
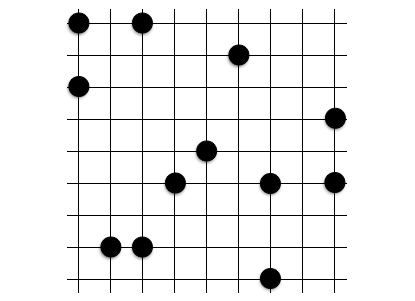
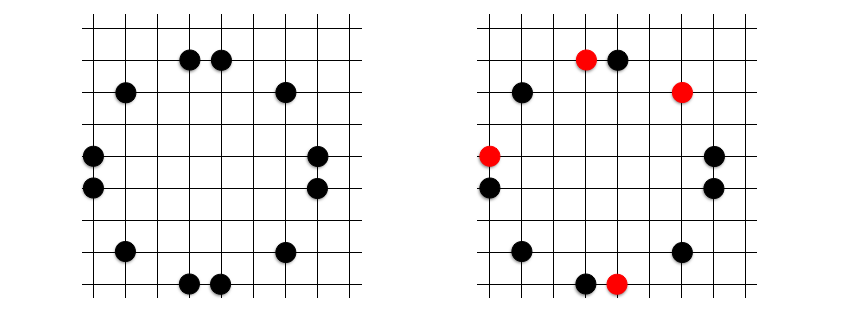
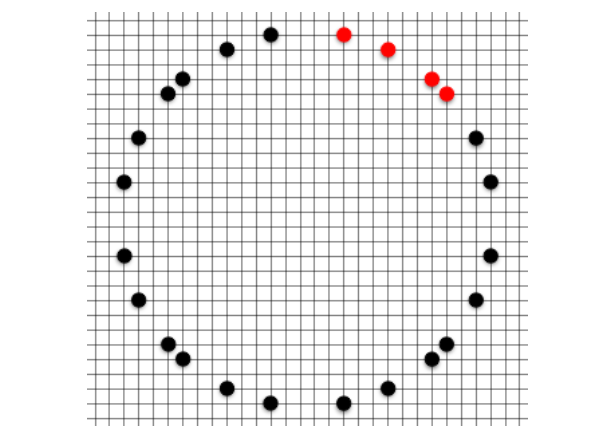
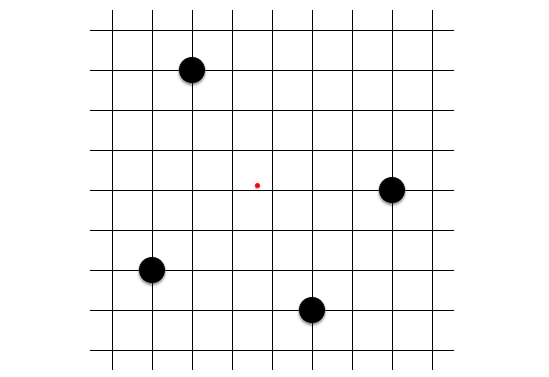
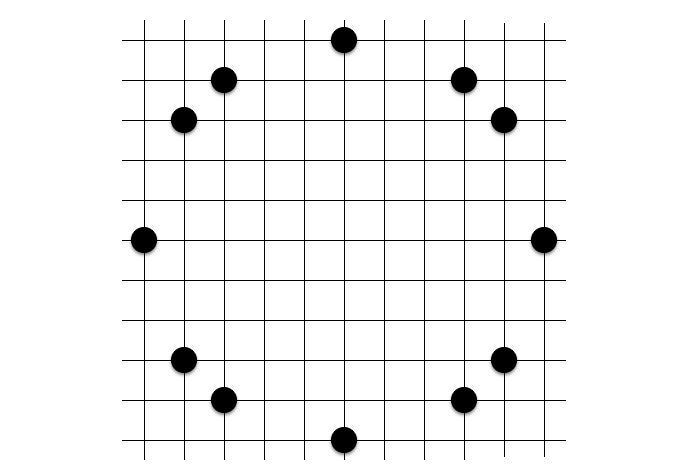
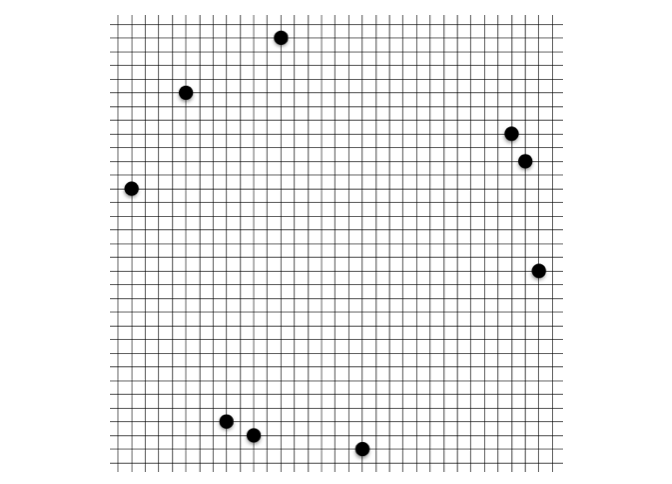
実際にプレイしてみると、予想以上にあちこちに共円が発生してしまうことがわかります。早速ですが、以下の盤面の中に共円があります。その共円を指摘できるでしょうか?
答えは記事の最後に載せたいと思います。このように、何個かの石が置かれた盤面上から共円を見つけ出すパズルを詰共円といいます。共円のトレーニングに有効です。共円開発者の 1 人にして、AtCoder のコンテストマネージャーのりんごさんも詰共円問題集を公開しています。
詰共円を少しやってみるとわかることは、
共円を指摘できるようになるためには、共円のパターン (共円定石) をある程度知る必要がある
ということになります。共円には本当に多彩で豊かな定石がたくさんあります。次章にて九路盤に登場する定石のすべてを一挙大公開します!!!!!
1-3. 共円のサイト・アプリ
これまでたくさんの共円愛好家によって、共円対戦や、詰共円を楽しめるサイトやアプリが作られています!
これらのおかげで快適な共円ライフを送ることができます。
| サイト・アプリ | 作者 | 紹介 |
|---|---|---|
| 共円 | noboru さん | とにかくすごい量の詰共円問題が収録されています! |
| 詰め共円 | noboru さん | 同じ作者によるアプリ版もあります! |
| 共円 | Hanachiru さん | 共円対戦の楽しめるアプリです! |
| 共円 (Kyouen) | yambi さん | 置けない場所をすべて表示してくれる機能があり、共円対戦後の感想戦にとても役立ちます |
| 共円探し (Where's Kyoen?) | saito_ta さん | 詰共円だけでなく、共円チェックもできます |
| ゲーム 共円 (きょうえん) | フナハシ学習塾さん | 詰共円や共円対戦を楽しめます |
| ピクセル共円 | snuke さん | 雰囲気と運で遊ぶ共円です |
2. 共円定石
メジャーなものから超マイナーなものまで、九路盤定石をすべて公開します!!!
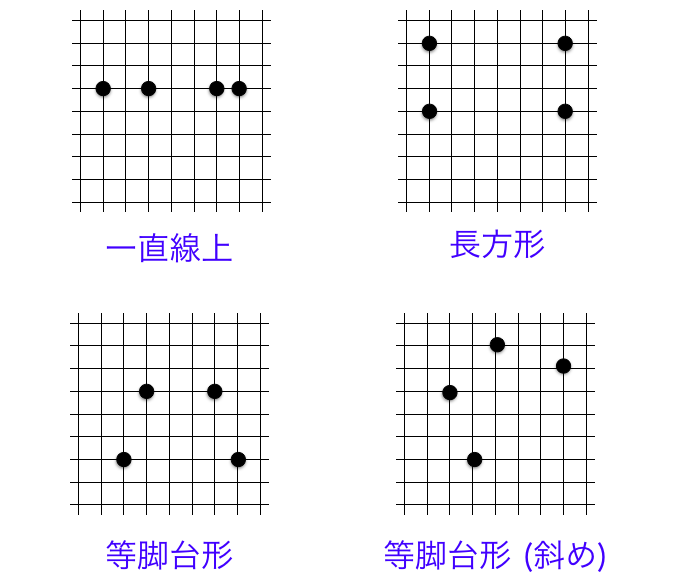
定石 0: 自明パターン
比較的自明な場合として
- 一直線上 (ルール)
- 長方形
- 等脚台形
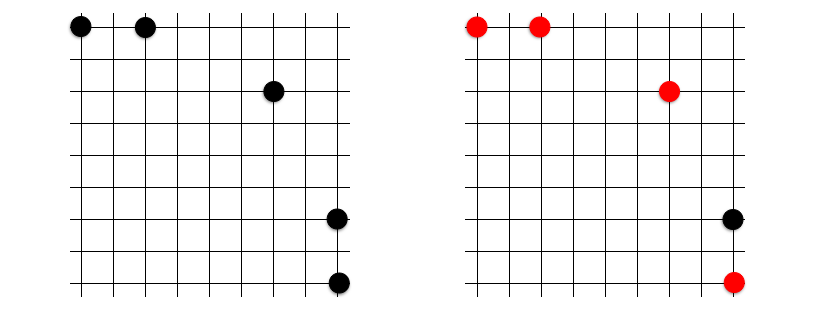
が挙げられます。いずれも共円であることが自明なパターンですが、このうち等脚台形については、斜め 45 度の等脚台形に注意が必要です。しばしば見逃してしまいます。
余談ですが「斜め 45 度じゃない等脚台形」も一応あります。例えば下図は確かに等脚台形になっています!3
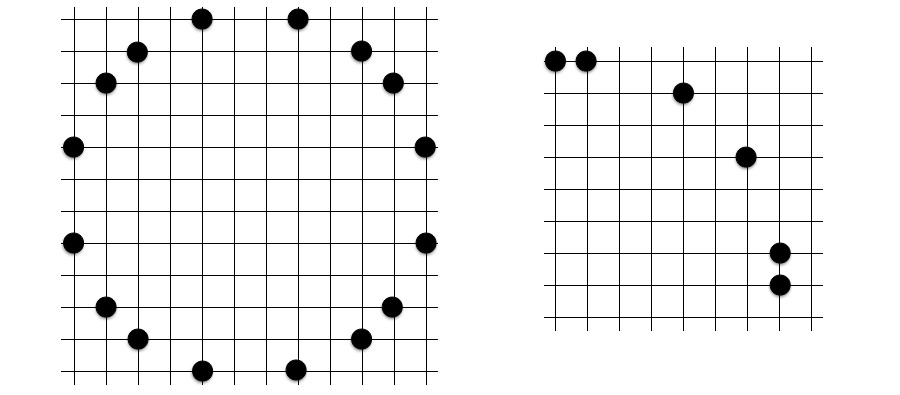
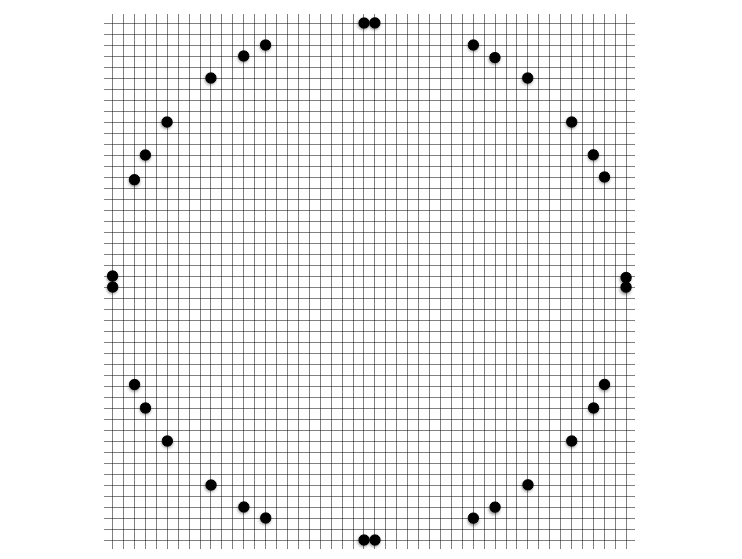
定石 1: 八角形
続いてこれも比較的わかりやすい八角形定石です。内角がすべて $135$ 度になっていて、対称性から共円になることが明快です。しかし右図のように 4 点だけを取り出すと、意外と指摘が難しいことがわかると思います。このような共円をほぼ確実に避けられるようになると脱初心者と言えるでしょう!
八角形定石のサイズにはバリエーションがあり、小さいものから大きいものまで様々です。
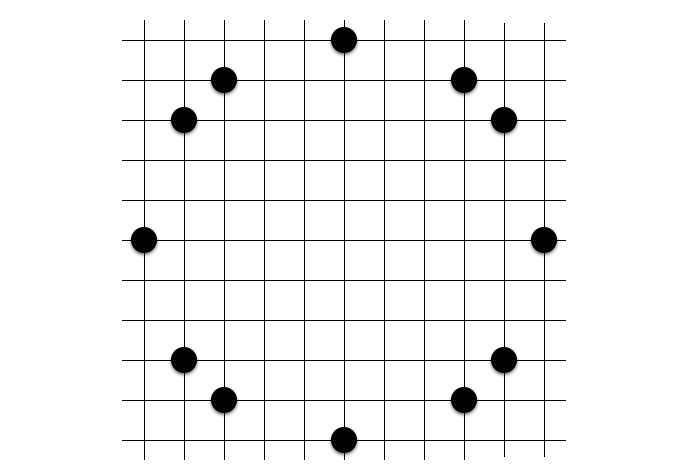
定石 2: 十二角形
この辺りから共円らしくなって来ます!
各マスの一辺の長さを $2$ と考えて、各点の中心からの距離を考えると、
$$7^2 + 1^2 = 5^2 + 5^2 = 50$$
という関係によって確かに共円になっていることがわかります。この後散々後述するのですが「整数を平方数の和に分解する方法が何通りあるか?」という問題の考察が共円定石を探る基本的な方法の 1 つになります。そこでガウス整数が大活躍するのです。
十二角形定石が指摘できるようになったり、意図的に仕掛けたりできるようになると、共円対戦が一気に楽しくなります。例えば右図のような 4 点がすぐに指摘できるようになると楽しいです。コツとしては「$5 × 5$ の正方形をイメージするとよい」とよく言われます。
なお自明定石を除くと、この十二角形定石は九路盤において最も出現頻度が高いことがわかっています。十二角形定石を指摘する場面はとても多いです。共円の登竜門と言えるでしょう。
また余談ですが、実はこの共円をそのままサイズを 2 倍にした共円の一部も九路盤の登場し得ます。面白いですね!
定石 3: 十二角形ダッシュ
半径 $5$ の定石です。$3^2 + 4^2 = 5^2$ といういわゆるピタゴラスの定理で有名な直角三角形を思い出すとごく自然に導かれる共円です。なお、九路盤に登場し得る十二角形は「十二角形」「その 2 倍」「十二角形ダッシュ」の 3 種類に限られることがわかっています。
定石 4: 六角形
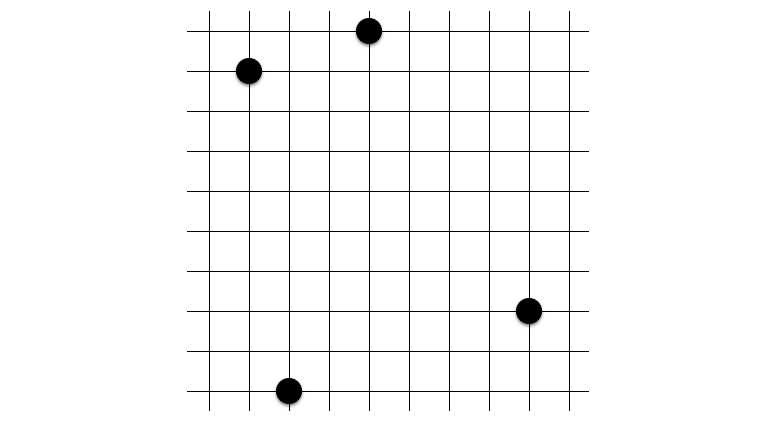
これも実戦で比較的よく見かける六角形です。こちらも $3^2 + 4^2 = 5^2$ の関係から自然に導かれます。

定石 5: 十六角形 4 種
この辺りから共円の深淵に入り込んだ気持ちになります。円の半径が大きいため、九路盤に登場し得るパターンは限られます。そのため慣れれば比較的見つけやすい定石です。なお九路盤に登場し得る十六角形は 4 種類に限られることがわかっています。それぞれ
- $11^2 + 3^2 = 9^2 + 7^2 = 130$ $(= 2 × 5 × 13)$ (左上、通称「β-十六角形」)
- $13^2 + 1^2 = 11^2 + 7^2 = 170$ $(= 2 × 5 × 17)$ (右上、通称「γ-十六角形」)
- $17^2 + 1^2 = 13^2 + 11^2 = 290$ $(= 2 × 5 × 29)$ (左下、通称「δ-十六角形」)
- $8^2 + 1^2 = 7^2 + 4^2 = 65$ $(= 5 × 13)$ (右下、通称「アルバニア」)
という関係によって共円であることがわかります。このうち最も半径の小さい共円のみ全体像を左上に示しています。
定石 6: 二十四角形
八角形、十二角形、十六角形と来たら次は二十四角形ですね4!!!!!!!
下図は半径が最小の二十四角形ですが、それでも相当に大きいです。このうち九路盤に登場し得るパターンは赤く示した部分だけです。この共円は
$25^2 + 5^2 = 23^2 + 11^2 = 19^2 + 17^2 = 650$ $(= 2 × 5^2 × 13)$
という関係によって成り立っています。実戦上は $(1, 1)$, $(2, 3)$, $(1, 3)$ と覚えればよいです。覚えてしまえば比較的見つけやすい共円だと思いますが、初心者はこれを指摘されても困惑するでしょう。。。これが共円であることを説明するときはトレミーの定理を用いるのがおススメです。
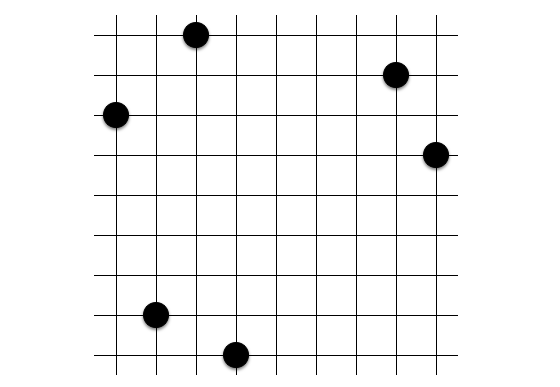
定石 7: いちご
まずは定石を見てみましょう!
共円を始めてから最初に衝撃を受ける定石だと思います。というのもここまでに登場した共円定石たちはすべて
- 中心が格子点上
- 中心が辺の中点だったり、マスの中心だったり
という感じで対称性が感じられるものばかりでした。しかしこの共円の中心は上図で赤く示したところにあり、$(\frac{1}{14}, \frac{5}{14})$ という中途半端な座標にあるのです (これが「いちご」の由来です)。そしてこの円周上の格子点はこの 4 点のみです!
これが共円であることの証明は方冪の定理を使えば簡単です。下図のように対角線同士が格子点上で交わっています。$\sqrt{5} × 2\sqrt{5} = \sqrt{10} × \sqrt{10} = 10$ より確かに共円になっています。
さて、この共円は一体何者なのでしょうか?その正体は「三十二角形定石を $1/7$ に縮小したもの」です。この三十二角形は
$47^2 + 1^2 = 43^2 + 19^2 = 41^2 + 23^2 = 37^2 + 29^2 = 2210$ $(= 2 × 5 × 13 × 17)$
という式によって構成されており、本質的に $4$ 通りもの分解が成立しています。中心が $(\frac{1}{2}, \frac{1}{2})$ にあって対称性があるうちは $4 × 8 = 32$ 個の頂点を生み出せていますが、$1/7$ に縮小して対称性を失うとヘンテコな四角形になるのは自然なことと言えます。なお、この三十二角形定石自体は九路盤には登場しないです。
定石 8: メキシコ
いちご定石の発見に触発された、国際数学オリンピックメキシコ大会 (2005 年) の日本代表メンバーが、同じく方冪の定理を駆使して発見した定石です。同大会中に発見されたことからメキシコ定石と呼ばれています。
これは先に出て来た二十四角形定石を $1/3$ に縮小したものであり、中心は $(\frac{1}{6}, \frac{1}{6})$ といった座標にあります。
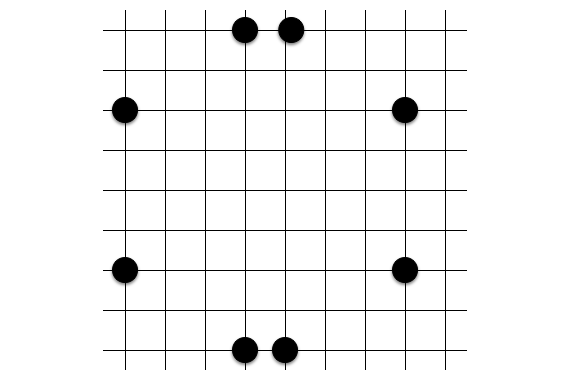
定石 9: 呪われた八角形 (通称「β-八角形」)
これも方冪の定理から自然に共円であることがわかります。八角形は八角形でも、内角が $135$ 度になっていなくてエキサイティングな八角形です。意外と知られていない定石ですが、何気に出現頻度は高く、実戦でも仕掛けやすいです。
これは十六角形定石 4 種で示したやつのうち、右下のやつを $1/2$ に縮小したもので、
$$(2x)^2 + (2y + 1)^2 = 5 × 13$$
で表される共円です。
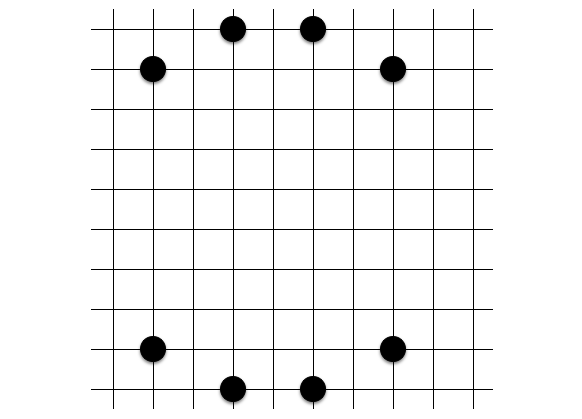
定石 10: 呪われた八角形 2 (通称「γ-八角形」)
定石 9: ダイヤモンド八角形と似ています。これは中心が $(0, \frac{1}{2})$ にあり、
$$(2x)^2 + (2y + 1)^2 = 5 × 17$$
で表される共円です。定石 9 の方は右辺が「$5 × 13$」でした。
定石 11: 呪われた八角形 3 (通称「キューバ」)
同じく中心は $(0, \frac{1}{2})$ にあって
$$(2x)^2 + (2y + 1)^2 = 5^3$$
で表される共円です。
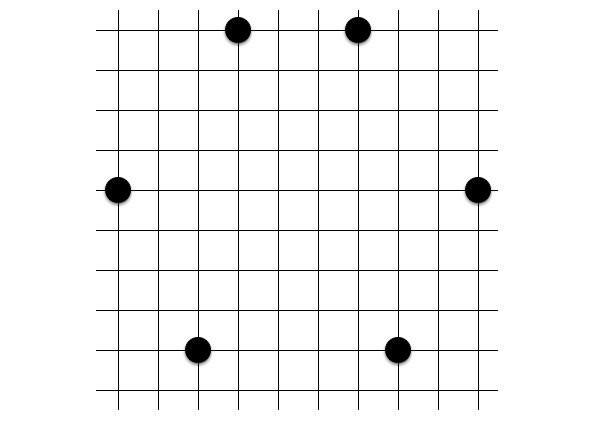
定石 12: えぐい六角形 (通称「β-六角形」)
なんとも不思議な六角形です。中心は $(\frac{1}{4}, \frac{2}{4})$ にあり、
$$(4x + 2)^2 + (4y + 1)^2 = 5^2 × 13$$
で表される共円です。
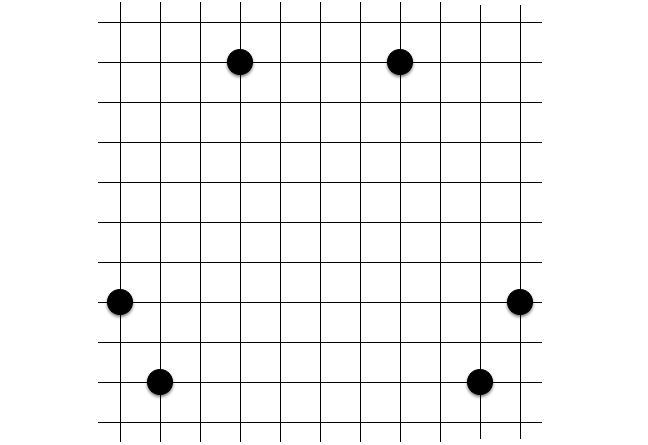
定石 13: えぐい六角形 2 (通称「γ-六角形」)
定石 12 の右辺が「$5^2 × 17$」バージョンです。
3. ガウス整数
共円定石を探訪するためのガウス整数の理論について、急ぎ足で外観してみます。
3-1. ガウス整数の導入
共円定石を探索する上では、正の整数 $N$ に対して
$$x^2 + y^2 = N$$
と分解する方法が何通りあるのかを考察することが重要そうに思えて来ます。一見手の付けられない難問に思えるのですが、
$$(x + yi)(x - yi) = N$$
としてみると、普通の整数を拡張して ${\mathbb Z}[i]$ = {$x + yi$ | $x$, $y$ $\in$ ${\mathbb Z}$} な世界を考察してみたくなります。このような整数をガウス整数もしくは複素整数と呼びます。そしてガウス整数の意味で $N$ を素因数分解して $x + yi$, $x - yi$ に素因子を振り分ければいいような気がして来ます。整数の世界を拡張したので
- ガウス素数の意味での素数をどう定義したらよい?
- 果たして素因数分解の一意性は成り立つのか?
- どんな数が素数になるのか?
といったことを一歩一歩考える必要があります。例えば、通常の整数では素数である $5$ は、ガウス整数の意味では
$$5 = (2+i)(2-i)$$
と分解できるため、素数ではありません。しかし実は $2+i$ や $2-i$ は素数であることが知られています。なお、今後通常の整数のことを有理整数と呼ぶこととします。
3-2. 約数・倍数
まずは整数の整除の基本概念である「約数・倍数」についてです。
ガウス整数 $\alpha$ が $\beta$ で割り切れるとは、あるガウス整数 $\gamma$ が存在して $\alpha = \beta \gamma$ と表せることと定義するのがとりあえず自然でしょう。
3-3. ノルム
ガウス整数の世界を、有理整数の世界のアナロジーとして考える上で重要なノルムの概念を導入します。とても単純で以下の通りです。
ガウス整数 $z = x + yi$ に対して、ノルム $N(z)$ を
$$N(z) = x^2 + y^2$$
と定義する。
ノルムを考える理由の 1 つとしては、将来ガウス整数 $\alpha$ を "素因数分解" して
$$\alpha = \beta \gamma \dots$$
となったときに両辺のノルムをとると
$$N(\alpha) = N(\beta)N(\gamma) \dots$$
となって、有理整数に関する式になります。このように有理整数の世界との対応をとることで、ガウス整数に関する理解を深めることができます。また、ノルムの言い換えとして、$z = x + yi$ の共役複素数を $\bar{z} = x - yi$ として
$$N(z) = z\bar{z}$$
とも表せます。
「$\alpha$ が $\beta$ で割り切れるならば、$\bar{\alpha}$ が $\bar{\beta}$ で割り切れる」
ということを考えると、
「$\alpha$ が $\beta$ で割り切れるならば、有理整数の意味で $N(\alpha)$ が $N(\beta)$ で割り切れる」
という性質が導かれます。
3-4. 単数
まずはガウス整数の整除を考える上で基本になる「単数」の概念を導入します。
すべての整数の約数となる整数を単数という
つまり「$1$ の約数」です。単数同士の積も単数になります。有理整数の世界では単数は $\pm{1}$ のみでした。複素整数での単数は
$$\pm{1}, \pm{i}$$
の $4$ つです。この証明に早速ノルムが使えます。$\epsilon = x + yi$ を単数とすれば $\epsilon$ は $1$ で割り切れることから、$N(\bar{\epsilon}) = x^2 + y^2$ が有理整数の意味で $N(1) = 1$ で割り切れます。そのような $x, y$ の組は
$$(x, y) = (\pm{1}, \pm{1})$$
しかありません (複合任意)。以上からガウス整数における単数は $\pm{1}$, $\pm{i}$ の 4 つであることがわかりました。
単数の意味
単数の意味合いとしては、ガウス整数を単数倍してもガウス整数の整除に影響を与えないことが言えます5。具体例として $5$ が $2 + i$ の倍数であることから、$5$ が $i(2+i) = -1 + 2i$ の倍数でもあることが言えます。
ガウス整数の素因数分解において、単数倍したものは同じものとみなします。例えば
$$5 = (2 + i)(2 - i) = (-1 + 2i)(-1 - 2i)$$
は同じ素因数分解だとみなします。
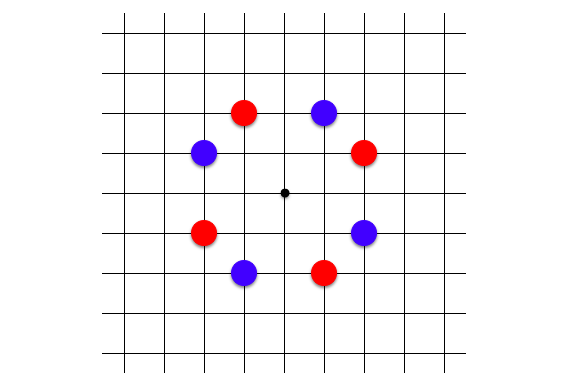
共円における単数
例えば中心が $(0, 0)$ で半径の二乗が $5$ なものを考えてみます。これは $z\bar{z} = 5$ を満たすガウス整数 $z$ を見つける問題だとみなせます。単数倍を除くと解は、$z = 2 + i, 2 - i$ の $2$ 個があります。単数倍を含めて考えると
- 複素数 $2 + i$ とその単数倍 (によって 4 個、赤丸で示した)
- 複素数 $2 - i$ とその単数倍 (によって 4 個、青丸で示した)
で合計 $8$ 個の格子点を有していて八角形定石を形成していることがわかります。ここで $2 + i$ と $2 - i$ とは本質的に異なるものとみなした方が後々よいです。
3-5. 素数
有理整数では素数の定義は
- $1$ と自分自身でしか割ることのできない数
でした。つまり素因数分解を試みたときにそれ以上分解できない数を素数と呼んでいたわけです。ガウス整数でも同じように
- $1$ と自分自身でしか割ることのできない数
を素数6と呼ぶことにします。ただし単数倍は無視します。より正確に言うならば以下のように言えるでしょう。
ガウス整数 $\pi$ が素数であるとは、$\pi$ の約数が $\pm{1}, \pm{i}, \pm{\pi}, \pm{i\pi}$ のみであること
さて、ガウス素数を探る上でやはりノルムが重要な道具になります。しかしここから先はいよいよ「ガウス整数での素因数分解の一意性」が必要になります!本当はそれをちゃんと示す必要がありますが、それは後で概略だけ補足することとして、素因数分解の一意性が成り立つものとして議論を進めて行きます。
$\pi$ がガウス素数であるとき、
- 有理素数 $p$ が存在して、$N(\pi) = p$ または $p^2$ である
ということが言えます。これを簡単に示します。
【証明】
$\pi$ の倍数のうち、有理整数でもある最小の数を $p$ とする7と $p$ は素数でなければなりません。なぜなら $p$ が素数でないとすると $p = ab$ ($a, b$ は $1$ 以上の有理整数) と表せますが、このとき $ab$ が $\pi$ の倍数なので $a$ または $b$ が $\pi$ で割り切れることになります (ここで素因数分解の一意性の大元になる重要な性質を使っています)。これは $p$ の最小性に矛盾します。
さて、$\pi \kappa = p$ ($\kappa$ はガウス整数) とおいて両辺のノルムをとると
$$N(\pi)N(\kappa) = p^2$$
となります。よって $N(\pi)$ は $p^2$ の約数であり、$N(\pi) = p$ または $p^2$ が成立します。
(証明終)
3-6. ガウス素数をすべて求める (前半)
いよいよガウス整数における素数をすべて特定する作業にかかります。前節の議論からガウス素数 $\pi$ に対しては、通常の整数での素数 $p$ が一意に存在して
- $N(\pi) = p$
- $N(\pi) = p^2$
のいずれかであることがわかりました。前者について、逆に有理素数 $p$ に対して $N(\pi) = p$ が成立するとき、$\pi$ がガウス素数になることがわかります。なぜなら、$\pi = \alpha\beta$ とすると $N(\alpha)N(\beta) = p$ となることから $N(\alpha) = 1$ または $N(\beta) = 1$ となり、$\alpha$ か $\beta$ は必ず単数になります。したがって $\pi$ はガウス素数です。
後者は $\pi\bar{\pi} = p^2$ より $\pi = \bar{\pi} = p$ であることがわかります。つまり前者のパターンに当てはまらないようなガウス素数は有理整数の意味でも素数になっていることがわかります。一方 $N(\pi) = p$ となるような $\pi$ が存在しないような有理素数 $p$ を考えると、それはガウス整数の意味でも素数になっていることがわかります。なぜなら $p = \alpha \beta$ とすると両辺のノルムをとって $p^2 = N(\alpha)N(\beta)$ となりますが、$N(\alpha) \neq p$, $N(\beta) \neq p$ でなければならないので、$N(\alpha) = 1$ または $N(\beta) = 1$ が成り立ちます。つまり $\alpha$ または $\beta$ は単数でなければならず、$p$ はガウス素数です。
以上から、ガウス素数は以下で尽くされることがわかりました。
- $N(\pi) = p$ となる $\pi$ が存在するような有理素数 $p$ に対しての $\pi$
- $N(\pi) = p$ となる $\pi$ が存在しないような有理素数 $p$ に対しての $p$
したがって問題は、有理素数 $p$ に対して
$$x^2 + y^2 = p$$
の有理整数解 $(x, y)$ が存在するかどうかを判定し、存在するならば求める問題に帰着されたわけです。
3-7. ガウス素数をすべて求める (後半)
ガウス整数をすべて求める問題が初等整数論の問題に帰着されたので、それを考えます。
p = 2 のとき
まずは最も特殊な $p = 2$ の場合を考えます。
$$2 = (1 + i)(1 - i)$$
であるので、前者のパターンであることがわかります。つまり $1 + i$ や $1 - i$ がガウス素数です。
ここで超特異的なこととして、$1 + i$ と $1 - i$ は複素共役でありながら「互いに単数倍」の関係にもなっています!!!!!
こんなことは他の $p$ に対しては起こらないです。例えば $p= 5$ のときは $5 = (2 + i)(2 - i)$ と分解できて $2 + i$, $2 - i$ はガウス素数なのですが、これらは「互いに単数倍」の関係にはなっていません。
この特異性が後に共円を考えるときに効いて来ます。しばしば $1 + i$ やその単数倍を $\lambda$ と表記します。単数倍を除いて考えると $\lambda^2 = 2$ であると言ってよいでしょう。ガウス整数の世界では
- $\lambda$ で割り切れる数: 偶数
- $\lambda$ で割り切れない数: 奇数
と考えるとしっくり来ます。
p ≡ 3 (mod. 4) のとき
$p \equiv 3 \pmod 4$ のケースが比較的簡単です。よく大学入試でも $x^2 + y^2$ が $4$ で割って $3$ あまることはあり得ないことを証明させる問題が出題されますね。
すなわち
- $x^2 \equiv 0$ または $1 \pmod 4$
- $y^2 \equiv 0$ または $1 \pmod 4$
なので $x^2 + y^2$ を $4$ で割ったあまりは $0, 1, 2$ のいずれかになります。つまり $x^2 + y^2 = p$ を満たす有理整数 $(x, y)$ は存在せず、$p$ は有理素数でもあると同時にガウス素数でもあるということになります。
p ≡ 1 (mod. 4) のとき
残るは $p$ が $4$ で割って $1$ あまる素数の場合です!!!!!
実は Fermat の二平方定理と呼ばれる以下の定理が知られています。
$p$ を $4$ で割って $1$ あまる有理素数とするとき、$x^2 + y^2 = p$ を満たす整数 $x, y$ ($x \ge y \ge 0$) が一意に存在する
この二平方定理において、もし存在性が言えたならば、実は一意性はすでにわかっています。何故なら $p = (x + yi)(x - yi)$ を満たす $x + yi$ がもし存在するならば、$x + yi, x - yi$ はともにガウス素数だからです。$p = (x + yi)(x - yi)$ はガウス素数の世界での $p$ の素因数分解になっているということなので、素因数分解の一意性から、定理を満たす $(x, y)$ の一意性が従います。
さて、ここで Euler の規準と呼ばれる定理があります。別名「平方剰余の第一補充則」とも呼ばれています。
$p$ を $4$ で割って $1$ あまる素数とするとき、$x^2 \equiv -1 \pmod p$ を満たす整数 $x$ が存在する。
これを認めてしまえば Fermat の二平方定理の証明は簡単です。すなわち、$(x + i)(x - i)$ が $p$ で割り切れることになるので、もし有理素数 $p$ がガウス素数でもあるとすると、$x+i$ または $x-i$ が $p$ で割り切れることになります (ここでも素因数分解の一意性の大元となる性質を使っています)。しかし $x+i$ や $x-i$ は $p$ で割れないので矛盾です。従って $p$ はガウス素数ではないこととなり、$N(\pi) = p$ を満たすガウス整数 $\pi$ が存在することになります。
残るは Euler の規準の証明です。これの証明のためには、原始根を用います。Fermat の小定理は、$p$ の倍数でない整数 $a$ に対して
$$a^{p-1} \equiv 1 \pmod p$$
を主張するものですが、$a$ が原始根であるとは、$0 < e < p-1$ に対しては $a^e \equiv 1 \pmod p$ が成立しないことを言います。そしてこのような原始根が必ず存在することが知られています (今回はこの証明は省略します)。原始根を $r$ とすると
$$r^{p-1} \equiv 1 \pmod p$$
より
$$(r^{\frac{p-1}{2}} + 1)(r^{\frac{p-1}{2}} - 1) \equiv 0 \pmod p$$
となりますが、$r$ は原始根なので $r^{\frac{p-1}{2}} - 1$ は $p$ の倍数ではないです。よって $r^{\frac{p-1}{2}} + 1$ が $p$ の倍数ということになって
$$(r^{\frac{p-1}{4}})^2 \equiv -1 \pmod p$$
が従います。$p$ は $4$ で割って $1$ あまる素数なので $\frac{p-1}{4}$ は整数です。以上から具体的な $x$ が構成できました。
(証明終)
まとめ
ガウス素数は以下の通りであることがわかりました。
- $\lambda$ ($1 + i$ の単数倍)
- $4$ で割って $3$ あまる有理素数 $p$
- $4$ で割って $1$ あまる有理素数 $p$ に対して $N(\pi) = p$ を満たす $\pi$ が存在して、その $\pi$
3-8. x^2 + y^2 = N の解
ガウス整数における素数が確定したので、いよいよ $x^2 + y^2 = N$ の整数回について考察してみましょう。いきなり一般論だと頭がこんがらがるので、特殊な場合から徐々に考えていきたいと思います。
x^2 + y^2 = 5
まずは簡単な場合です。すでに考察したように、$z = x + yi$ とおいて
$$z\bar{z} = (2 + i)(2 - i)$$
を満たす $z$ は単数倍を除くと
- $z = 2 + i$
- $z = 2 - i$
の $2$ 通りがあります (Fermat の二平方定理ではさらに複素共役も同一視して一通りと主張していました)。
単数倍を考慮すると $2 × 4 = 8$ 通りの解があります。これはちょうど以下のような共円に対応していることもすでに述べた通りです。

x^2 + y^2 = 5^2
すこしレベルを上げて $N = 5^2$ としてみましょう。このとき $z = x + yi$ として
$$z\bar{z} = (2 + i)^2 (2 - i)^2$$
となります。$z$ と $\bar{z}$ とが共役であることを意識しながら、両者に $2 + i$, $2 - i$ をうまく振り分けることになります。これを満たす $z$ (と $\bar{z}$) は単数倍を除いて以下の $3$ 通りになります。
| $z$ | $\bar{z}$ |
|---|---|
| $(2+i)^2$ | $(2-i)^2$ |
| $(2+i)(2-i)$ | $(2+i)(2-i)$ |
| $(2-i)^2$ | $(2+i)^2$ |
展開するとそれぞれ
- $z = 3 + 4i$
- $z= 5$
- $z = 3 - 4i$
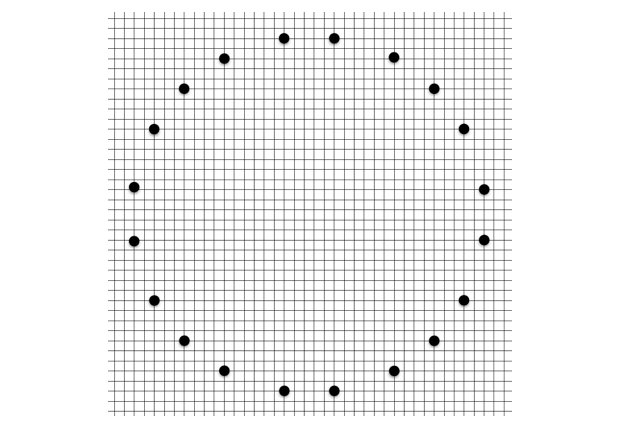
となります。単数倍を入れると $3$ × $4$ = $12$ 個の解があります。これはちょうど以下の「十二角形ダッシュ」に対応しています!
x^2 + y^2 = 5^3 × 13
さらにレベルを上げて $N = 5^3 × 13$ としてみます。今度は
$$z\bar{z} = (2 + i)^3 (2 - i)^3 (3 + 2i) (3 - 2i)$$
となります。これを満たす $z$ は以下のように単数倍を除いて $8$ 通りになります。
| $z$ | $\bar{z}$ |
|---|---|
| $(2+i)^3(3+2i)$ | $(2-i)^3(3-2i)$ |
| $(2+i)^3(3-2i)$ | $(2-i)^3(3+2i)$ |
| $(2+i)^2(2-i)(3+2i)$ | $(2+i)(2-i)^2(3-2i)$ |
| $(2+i)^2(2-i)(3-2i)$ | $(2+i)(2-i)^2(3+2i)$ |
| $(2+i)(2-i)^2(3+2i)$ | $(2+i)^2(2-i)(3-2i)$ |
| $(2+i)(2-i)^2(3-2i)$ | $(2+i)^2(2-i)(3+2i)$ |
| $(2-i)^3(3+2i)$ | $(2+i)^3(3-2i)$ |
| $(2-i)^3(3-2i)$ | $(2+i)^3(3+2i)$ |
これらによって
$$z = 40 \pm 5i = 37 \pm 16i = 35 \pm 20i = 29 \pm 28i$$
という $8$ 通りの解が生まれるので単数倍を考慮すると $32$ 個の解があります。これはいちご定石で登場した三十二角形とは異なるものですが、三十二角形を形成することになります。
x^2 + y^2 = (4 で割って 1 あまる素因子のみ)
ここまで来ると一般論も見えて来るのではないでしょうか。まず $N$ を有理整数の意味で素因数分解したときに $4$ で割って $1$ あまる素因子のみが登場する場合を考えます。このとき
$$z\bar{z} = (\pi_1^{e_1} \bar{\pi_1}^{e_1}) (\pi_2^{e_2} \bar{\pi_2}^{e_2}) \dots (\pi_k^{e_k} \bar{\pi_k}^{e_k})$$
という風になります。これを満たす $z$ は単数倍を除いて
$$z = (\pi_1^{f_1} \bar{\pi_1}^{e_1 - f_1}) (\pi_2^{f_2} \bar{\pi_2}^{e_2 - f_2}) \dots (\pi_k^{f_k} \bar{\pi_k}^{e_k- f_k})$$
の形をしていることがわかります。これの個数は $(e_1 + 1)(e_2 + 1) \dots (e_k + 1)$ 個です。単数倍を考慮すると全部で $4(e_1 + 1)(e_2 + 1) \dots (e_k + 1)$ 個の解があります。
x^2 + y^2 = N
いよいよ一般の場合を考察します。$N$ をガウス素数の意味で素因数分解して
$$z\bar{z} = \lambda^d (\pi_1^{e_1} \bar{\pi_1}^{e_1} \dots \pi_k^{e_k} \bar{\pi_k}^{e_k})(p_1^{f_1} \dots p_l^{f_l})$$
と表せたとします。ただし $\pi_i$ は $4$ で割って $1$ あまる有理素数を分解して得られるガウス素数、$p_j$ は $4$ で割って $3$ あまる有理素数であってガウス素数でもあるもの、とします。注意点として、$\pi_i$ タイプの素因子は必ず複素共役とセットで登場しますし、同じ理由から $\lambda$ の指数 $d$ は必ず偶数となります。
議論はそれほど難しくないので結論だけ示したいと思います。
正の整数 $N$ に対して $x^2 + y^2 = N$ の解が存在する必要十分条件は、$N$ を素因数分解したとき、すべての $4$ で割って $3$ あまる素因子について指数が偶数であることである。
またこの条件を満たすときの解の個数は、$N$ を素因数分解したときの $4$ で割って $1$ あまる素因子の部分だけを $q_1^{e_1} q_2^{e_2} \dots q_k^{e_k}$ とするとき、$4(e_1 + 1)(e_2 + 1) \dots (e_k + 1)$ 個である。
3-9. 素因数分解の一意性
有理整数において素因数分解が重要な道具たりえたのは、素因数分解の一意性が成り立つからでした。ガウス整数においても素因数分解の一意性が成り立つことが、整数をガウス整数に拡張することを有益たらしめる理由であると言えます。実は「有理整数」「ガウス整数」にはともに
- ユークリッドの互除法が適用できる
という共通の構造があります。環論において一般に以下のような定理が成り立っています:
- ユークリッド整域は単項イデアル整域である
- 単項イデアル整域は一意分解整域である (素因数分解の一意性が成り立つ)
ユークリッド整域とはざっくり、ユークリッドの互除法が適用できる世界のことを言います。有理整数の世界も複素整数の世界もユークリッド整域になっていることは、それほど難しくない議論で示すことができます。
そして $R$ が単項イデアル整域であるとは {$a_1 x_1 + a_2 x_2 + ... + a_n x_n | x_1, x_2, ..., x_n \in R$} で表される元がすべて単一の元 $d$ の倍数になるようなもののことを言います。さて、有理整数の世界でよく知られる
$a_1 x_1 + a_2 x_2 + ... + a_n x_n = b$ を満たす整数 $(x_1, x_2, \dots, x_n)$ が存在する必要十分条件は $b$ が ${\rm GCD}(a_1, a_2, \dots, a_n)$ の倍数であること
という性質があります。このページで証明していますが、これはまさに「ユークリッド整域が単項イデアル整域であること」の証明の特殊ケースになっています。一般論もほぼ同様にして証明することができます。
さらに単項イデアル整域において素因数分解の一意性が成立することを示すには、「既約元」「素元」という概念を定義して、それらの等価性を示していくことになります。それほど難しい議論ではないので、
といった書籍たちを参考にしていただけたらと思います。
4. 共円定石探索へのガウス整数の応用
いよいよガウス整数の理論を用いて、共円定石について考察したいと思います。
4-1. 中心が格子点でない場合の一般論
すでに我々は「中心が格子点」である場合の共円については、「3-8. x^2 + y^2 = N」で考察を終えました。ここからは中心が一般の場合を考えて行くことになります。まず大前提として
円周上に $3$ 個以上の格子点をもつとき、その円の中心は有理点である
ということが言えます。これは、格子点を三頂点にもつ三角形の外心を具体的な式で書き下そうとしてみるとわかります。よって我々の考察の対象となる円は
$$(dx + a)^2 + (dy + b)^2 = N$$
という形のものになります。例えば十二角形定石は $d = 2$ の式になっていますし、いちご定石は $d = 14$ の式になっています。$z = x + yi$ とおいてこの式を書き直すと
$$(dz + (a + bi))\overline{(dz + (a + bi))} = N$$
となります。つまりこのガウス整数解を求める問題は
$z'\bar{z'} = N$ の解 $z'$ のうち、$d$ で割ったあまりが $a + bi$ のものを選ぶ
という問題になります。ここから ${\mathbb Z}[i]/d{\mathbb Z}[i]$ な世界を考察するという深淵な世界に入って行くことになります。ここでは深く立ち入らず、いい感じの性質をいくつか証明してみたいと思います。
4-2. 中心 (1/2, 1/2) について
今までに見て来た共円定石は中心が $(0, 0)$ なものと同じくらい、$(\frac{1}{2}, \frac{1}{2})$ なものも綺麗な対称性がありました。少し考えてみると以下のことが成り立ちます。
$N$ を奇数とする。
$z\bar{z} = 2N$ を満たす任意のガウス整数 $z$ は $2$ で割って $1+i$ あまる。
【証明】
$z\bar{z} = 2N$ を満たす $z$ は「$\lambda$ では割り切れるが、$\lambda^2 (= 2$ の単数倍) では割りれない数」となる。よって $z$ を $2$ で割ったあまりは $\lambda = 1+i$ になります。
(証明終)
$z\bar{z} = 2N$ の解と $z\bar{z} = N$ の解とは一対一対応していたことを思い出すと (前者の解は後者を $\lambda$ 倍したもののみです)、
$$(2z + (1+i))\overline{(2z + (1+i))} = 2N$$
の解と
$$z\bar{z} = N$$
の解も一対一対応しているということになります。半径としては $2N$ 型の方が小さくなり、半径の大きさの比は $1 : \sqrt{2}$ ですね。今まで見て来た共円が、半径 $2N$ 型が多かったのはそのためです。下図のように、「十二角形定石」と「半径 5 定石」はまさにこの関係になっています。
| 定石 | 式 |
|---|---|
| 十二角形定石 | $(2z + (1+i))\overline{(2z + (1+i))} = 2 × 5^2$ |
| 半径 5 定石 | $z\bar{z} = 5^2$ |
他にも以下の 2 つの十六角形定石も同じ関係になっています。
| 定石 | 式 |
|---|---|
| 十六角形定石 1 | $(2z + (1+i))\overline{(2z + (1+i))} = 2 × 5 × 13$ |
| 十六角形定石 4 | $z\bar{z} = 5 × 13$ |
以上に述べたことはさらに一般の有理点の共円にも一般化できて、$N, d$ を奇数として
$$(dz + \alpha)\overline{(dz + \alpha)} = N$$
のガウス整数解 $z$ に対し
$$(2dz + \beta)\overline{(2dz + \beta)} = 2N$$
のガウス整数解 $z$ との間に一対一対応があるように $\beta$ をとることができます。半径の比はやはり $\sqrt{2} : 1$ になっています。また $N$ は奇数としましたが「$2$ で偶数回割り切れる数」としても同様の結論が得られます。
4-3. ちょうど n 点の共円の存在
様々な定石に触れると、自然な問題意識として「円周上にちょうど $n$ 点の格子点をもつ共円はあるか?」という問いが生まれます。そして存在することが自然に示せます。
$n$ を正の整数とする。
$$(3z + 1)\overline{(3z + 1)} = 13^n$$
は円周上にちょうど $n+1$ 個の格子点をもつ
【証明】
まず $z\bar{z} = (-2+3i)^n(-2-3i)^n$ の整数解は
「$z = (-2 + 3i)^a(-2 - 3i)^{n-a}$ とその単数倍」
で与えられることに注意します。各 $a$ に対して $z = (-2 + 3i)^a(-2 - 3i)^{n-a}$ の単数倍のうち、$3$ で割って $1$ あまるものはただ 1 つ存在します。よって $(3z + 1)\overline{(3z + 1)} = (-2+3i)^n(-2-3i)^n$ の整数解の個数はちょうど $n+1$ 個です。
(証明終)
4-4. 任意の有理点を中心とした共円の存在
さらに、いかなる有理点に対しても、それを中心にもつような共円があるのかという問題も気になります。これも肯定的に解決され、以下のことが言えます。
$a, b, d$ を有理整数とする。
$$(dz + (a + bi))\overline{(dz + (a + bi))} = (a^2 + b^2)(1+d^2)^n$$
の円周上に少なくとも $n+1$ 個の格子点がある
【証明】
$\alpha = a + bi$ とおいて、円の式を変形すると
$$(dz + \alpha)\overline{(dz + \alpha)} = \alpha\bar{\alpha}(1 + di)^n(1 - di)^n$$
になります。まず $z\bar{z} = \alpha\bar{\alpha}(1 + di)^n(1 - di)^n$ を満たすガウス整数 $z$ として
- $z = \alpha(1+di)^n$
- $z = \alpha(1+di)^{n-1}(1-di)$
- $z = \alpha(1+di)^{n-2}(1-di)^2$
- $\dots$
- $z = \alpha(1-di)^n$
の $n+1$ 個がとれるが、これらはいずれも $d$ で割って $\alpha$ あまります。よって
$$(dz + \alpha)\overline{(dz + \alpha)} = \alpha\bar{\alpha}(1 + di)^n(1 - di)^n$$
を満たすガウス整数 $z$ は少なくとも $n+1$ 個存在します。
(証明終)
このことから特に
三頂点がすべて格子点であるような三角形を格子点三角形と呼ぶことにするとき、
(格子点三角形の外心全体のなす集合) = (有理点全体の集合)
が成立する
ということが言えます。これ単体で見ると結構非自明で面白いかなと思います。
5. 共円定石つづき
ここまでで九路盤で登場し得る共円定石のすべてが出そろいました。簡単なものから、相当マニアックなものまで、よりどりみどりの定石たちです。しかし九路盤から拡げて行くとまだまだ豊かな共円たちが登場します。個人的に好きな定石たちを紹介してみます。
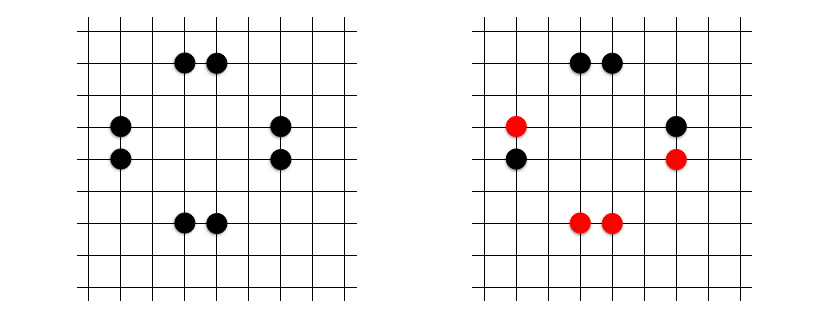
定石 14: えぐい等脚台形
冒頭で紹介したやつですね。「斜め 45 度な等脚台形以外でちょうど 4 点の等脚台形定石は存在するか?」という問題を肯定的に解決する定石です。実はいちご定石の親戚で、これも例の三十二角形定石を $1/5$ に圧縮したものです。

定石 15: 五角形
My Favorite 定石です。見た目は正五角形と見間違うほど綺麗です。中心は $(\frac{1}{6}, \frac{1}{6})$ で、円の式の右辺に出てくる値は $2 × 5^4$ です。
定石 16: 超綺麗な二十角形
上の五角形は、この二十角形を $1/3$ に縮小したものでした。元々の二十角形もすごく綺麗です。
定石 17: 貝殻のような八角形
これも大好きな定石で、貝殻のように綺麗な八角形です。中心は $(\frac{1}{6}, \frac{1}{6})$、円の式の右辺に出て来る値は $2 × 5 × 13 × 17$ です。なのでこれもいちご定石の親戚と言えるでしょう。
定石 18: 九角形
世にも珍しい九角形です。中心は $(\frac{1}{6}, \frac{1}{6})$、円の式の右辺の値は $2 × 5^2 × 13^2$ です。これを $3$ 倍に引き伸ばしたものは三十六角形になるわけですが、この九角形の時点ですでに結構大きいので、元の三十六角形は相当に大きそうです。
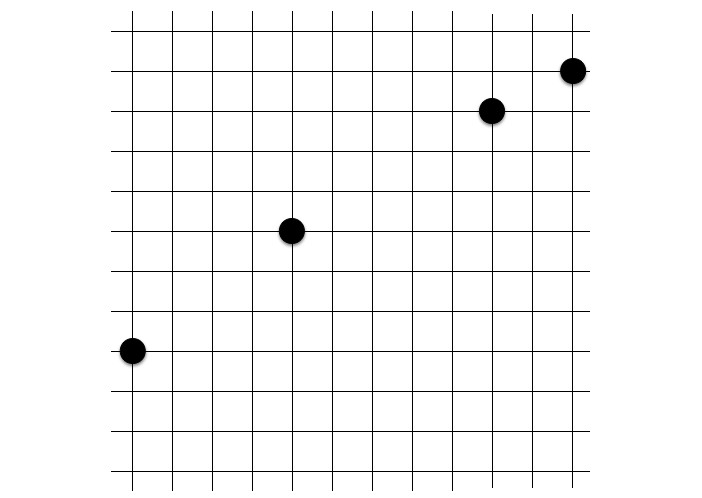
定石 19: 四十八角形の一部
九路盤の二十四角形定石もなかなかに直線に近くて不思議な感じでしたが、この四十八角形定石の一部も直線に近くて心躍ります。
6. 共円関数 --- 組合せ数学と整数論のダンス
少し趣向を変えて共円関数と呼ばれるものを紹介します。メチャクチャ考察要素があって楽しい話題です。問題意識として「九路盤に最大で何個まで石を置けるんだろう」というのは自然です。実は $18$ 個であることがわかっています。つまり盤面に $19$ 個の石が置かれていたならば、必ず共円が存在することがわかっています。では
$n$ を正の整数とする
$n × n$ の盤上に最大で何個の石を置けるか?
という問題を考えたくなるでしょう。この値を $k(n)$ と表記して共円関数と呼んでいます。共円関数についてわかっていることを整理します。
6-1. 具体的な値
- $k(1) = 1$
- $k(2) = 3$
- $k(3) = 5$
- $k(4) = 7$
- $k(5) = 9$
- $k(6) = 11$
- $k(7) = 14$
- $k(8) = 15$
- $k(9) = 18$
こうして見ると、$\lim_{n \to \infty} \frac{k(n)}{n} = 2$ と予想したくなりますね。
6-2. 上から抑える
まず自明なこととして「一直線上の 4 点は共円」というルールから、$k(n) \le 3n$ がわかります。もう少し賢い評価があります。tos さんによって示されました。アイディアとしては「どの 4 点も等脚台形にならないように」をきちんと評価してあげます。
$$k(n) \le \frac{5n-3}{2} (n は任意の正の整数)$$
【証明】
各行に置かれた石の個数を考えた時、$3$ 個置かれている行の個数を $a$、$2$ 個置かれている行の個数を $b$、$1$ 個置かれている行の個数を $c$ とします。
- 行を共有する $2$ 個の石 $p, q$ の垂直二等分線
- それとは別の行を共有する $2$ 個の石 $r, s$ の垂直二等分線
とが一致するとき、$p, q, r, s$ は等脚台形を成すことに注意します。ありうる垂直二等分線の本数は
$$(n-1) + (n-2) = 2n-3$$
ですが、
- $3$ 個の石が置かれた行から発生する垂直二等分線の本数は $3$ 本
- $2$ 個の石が置かれた行から発生する垂直二等分線の本数は $1$ 本
- $1$ 個の石が置かれた行から発生する垂直二等分線の本数は $0$ 本
であることから
$$3a + b \le 2n-3$$
でなければならないことがわかります。これと $a + b + c \le n$ とから
$$3a + 2b + c \le \frac{1}{2}(3a + b) + \frac{3}{2}(a + b + c) \le \frac{2n-3}{2} + \frac{3n}{2} = \frac{5n-3}{2}$$
が従います。
(証明終)
6-3. 下から抑える
$y = x^2$ な二次関数な置き方をして行けば共円にならないことは比較的すぐにわかります。その発想に基づいて $k(n) \ge \sqrt{n}$ が言えます。この下からの評価を $O(n)$ にできないか...というのが重要な問題意識でした。最初に omeometo さんによってその壁が破られました。
アイディアとしては基本的には $y = x^2$ 上に石を置いて行くのですが、はみ出した部分については $\mod p$ で置いて行きます。
$p$ を任意の素数とするとき、以下が成立する:
$$k(p) \ge \lfloor \frac{p}{4} \rfloor$$
特に $n$ を任意の正の整数として、以下が成立する:
$$k(n) \ge \lfloor \frac{n}{8} \rfloor$$
【証明】
前半が示されれば、後半は $2$ 以上の整数 $n$ に対してはチェビシェフの定理から $\frac{n}{2} \le p \le n$ を満たす素数 $p$ がとれるので、
$$k(n) \ge k(p) \ge \lfloor \frac{p}{4} \rfloor \ge \lfloor \frac{n}{8} \rfloor$$
より後半が示されます。よって前半を示せばよいです。$x = 0, 1, \dots, \lfloor \frac{p}{4} \rfloor -1$ に対して
- $(x, y)$ ($y$ は $x^2$ を $p$ で割ったあまり)
の上に石を置いていったとき、どの $4$ 点も共円にならないことを示します。もし $x = a, b, c, d$ について共円になっていると仮定すると
\det
\begin{pmatrix}
a^2 + a^4 & a & a^2 & 1 \\
b^2 + b^4 & b & b^2 & 1 \\
c^2 + c^4 & c & c^2 & 1 \\
d^2 + d^4 & d & d^2 & 1
\end{pmatrix}
\equiv 0 \pmod p
が成立することとなります。これを展開すると
$$(a + b + c + d)(a - b)(a - c)(a - d)(b - c)(b - d)(c - d) \equiv 0 \pmod p$$
となる8が、$0 < a + b + c + d < p$ より $(a - b)(a - c)(a - d)(b - c)(b - d)(c - d)$ が $p$ で割り切れることとなり、$a, b, c, d$ が互いに相異なることと矛盾します。
(証明終)
その後このアイディアを改良して、yos さんによって特別な $n$ に対しては $k(n) \ge n$ が示されました。
$p$ を $4$ で割って $1$ あまる任意の素数とするとき、以下が成立する:
$$k(p) \ge p$$
すみません...この証明を持っていなくて紹介できないです。。。yos さん、もしこの記事を読んでいたら、今度の忘年会で教えてください。。。
yos さんによる証明が本人のツイートにて公開されました!
6-4. 現状と今後
共円関数は非常にシンプルで素朴な問題意識ながら、組合せ論的考察から整数論的考察まで楽しめるよい話題ですね。以上をまとめると現状わかっているのは
もし極限値 $\lim_{n \to \infty} \frac{p(n)}{n}$ が存在するならば、その値は $1$ 以上 $\frac{5}{2}$ 以下である
ということですね。現在もしこれ以上の進展があってそれをご存知な方がいたら、是非教えてください。
7. 共円 tips
ここまでで紹介しきれていない共円に関するトピックスを紹介します。
7-1. 共円式
今まで共円を表す式を
- $(4x + 2)^2 + (4y + 1)^2 = 5^2 × 13$
- $(2z + (1+i))\overline{(2z + (1+i))} = 2 × 5 × 13$
のように書いてきました。長いので簡潔に表す方法が提案されています。これらはそれぞれ
- $\alpha$^$2$ $\beta$ $(1,2)/4$
- $\alpha$ $\beta$ $^\prime (1,1)/2$
と表します。右辺は基本的には $4$ で割って $1$ あまる素因子で素因数分解されるのですが、
| 素因子 | ギリシャ文字 |
|---|---|
| $5$ | $\alpha$ |
| $13$ | $\beta$ |
| $17$ | $\gamma$ |
| $29$ | $\delta$ |
| ... | ... |
という風に素因子をギリシャ文字に対応させて行きます。基本的に素因子が大きくなればなるほど、$x^2 + y^2$ と分解する方法の数は変わらずに、共円の半径だけが大きくなってしまうので、$\delta$ よりも先のギリシャ文字はほとんど見かけません。また、素因子のうち $2$ は例外的で、$2$ の指数がいくつであっても $x^2 + y^2$ と分解する方法の数は変わらないです。その特殊性から、素因子が $2$ で割れる場合は特別視して共円式に $^\prime$ をつけます。
最後に $(1,2)/4$ といった中心を表す部分を付け加えて完成です。ただし中心が格子点の場合は省略します。
7-2. 九路盤における各定石の出現頻度
共円対戦をする上で、各定石の出現頻度を把握しておくことは重要です。りんごさんによって調べ上げられています。
以下の結果になるようです。
やはり十二角形は頻出ですね。そして β-八角形は知名度の低さの割に出現頻度が高いです。
| 定石 | 角形数 | 共円式 | 個数 | 確率 |
|---|---|---|---|---|
| 非共円 | $1634588$ | |||
| 共線 | $3156$ | $10.8$ % | ||
| 等脚台形 | $9888$ | $33.9$ % | ||
| 八角形 | $8$ | $8300$ | $28.5$ % | |
| 十二角形 | $12$ | $\alpha$^$2$ $^\prime (1,1)/2$ | $4536$ | $15.6$ % |
| β-十六角形 | $16$ | $\alpha$ $\beta$ $^\prime (1,1)/2$ | $640$ | $2.20$ % |
| β-八角形 | $8$ | $\alpha$ $\beta$ $(0,1)/2$ | $624$ | $2.14$ % |
| 六角形 | $6$ | $\alpha$^$2$ $(0,1)/2$ | $560$ | $1.92$ % |
| γ-十六角形 | $16$ | $\alpha$ $\gamma$ $^\prime (1,1)/2$ | $352$ | $1.21$ % |
| 十二角形ダッシュ | $12$ | $\alpha$^$2$ | $344$ | $1.18$ % |
| メキシコ | $6$ | $\alpha$^$2$ $\beta$ $^\prime (1,1)/6$ | $160$ | $0.55$ % |
| γ-八角形 | $8$ | $\alpha$ $\gamma$ $(0,1)/2$ | $160$ | $0.55$ % |
| δ-十六角形 | $16$ | $\alpha$ $\delta$ $^\prime (1,1)/2$ | $96$ | $0.33$ % |
| 二十四角形 | $24$ | $\alpha$^$2$ $\beta$ $^\prime (1,1)/2$ | $80$ | $0.27$ % |
| β-六角形 | $6$ | $\alpha$^$2$ $\beta$ $(1,2)/4$ | $72$ | $0.25$ % |
| いちご | $4$ | $\alpha$ $\beta$ $\gamma$ $^\prime (1,5)/14$ | $72$ | $0.25$ % |
| アルバニア | $16$ | $\alpha$ $\beta$ | $40$ | $0.14$ % |
| 十二角形二倍 | $12$ | $\alpha$^$2$ $^\prime$ | $32$ | $0.11$ % |
| キューバ | $8$ | $\alpha$^$3$ $(0,1)/2$ | $24$ | $0.082$ % |
| γ-六角形 | $6$ | $\alpha$^$2$ $\gamma$ $(0,1)/4$ | $16$ | $0.055$ % |
7-3. 共円の変種
共円変わり種を紹介します。共円は通常は格子上で行われるものですが、
- ダイヤモンド共円
- $1 : \sqrt{2}$ のマス目上の共円
を楽しんでいる人たちもいるようです。これらはそれぞれ ${\mathbb Z}[\omega]$, ${\mathbb Z}[\sqrt{-2}]$ な整数論を考えることで (素因数分解の一意性が成り立つので) 同様の定石探索ができると思います。しかし
- $1 : \sqrt{5}$ のマス目上の共円
を考えると ${\mathbb Z}[\sqrt{-5}]$ な整数論を考えることになりますが、これは素因数分解の一意性が成り立ちません。エキサイティングな世界かもしれません。
また、共円をさらに発展させた共二次曲線を楽しんでいる人たちもいるようです。二次曲線は一般に $5$ 点を決めると一つに決まることが多いので「どの $6$ 石も同一二次曲線上に乗らないようにする」というルールでプレイすることになります。他には三次元格子上でプレイする共球も考えられます。共球は「どの $5$ 石も同一球面上に乗らないようにする」というルールでプレイすることになります。
8. おわりに
共円楽しいです!
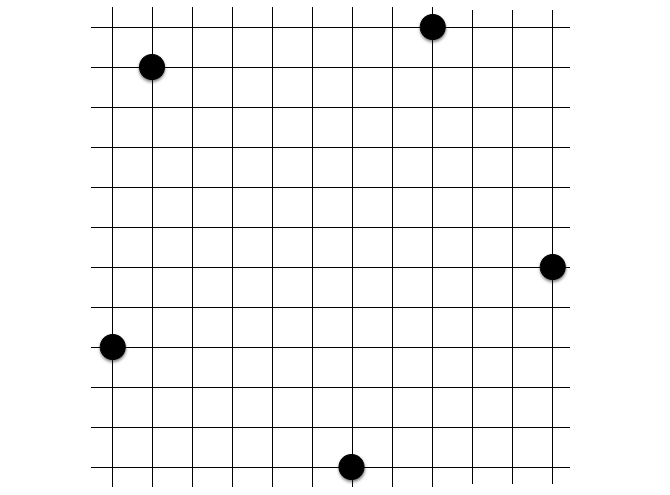
詰共円で紹介した問題の答えはこれでした。メキシコ定石の遠い 4 点は気づきにくいパターンの 1 つだと思います。
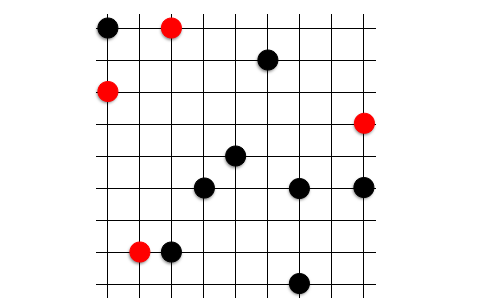
-
各企業の競技プログラマたちが集まってコンテストをするイベントです。 ↩
-
目隠し脳内共円はなかなかシビアで楽しいです!以前 yos さんと対戦して、十二角形定石を指摘されて負けました。 ↩
-
しかもこの円周上にはこの 4 点以外の格子点は通ってないのです。しかし九路盤の範囲内ではこのようなエグい等脚台形は無いことがわかっています。 ↩
-
自然な成り行きでは次は二十角形だと思われるのですが、二十角形より二十四角形の方が半径が小さくなりがちです。 ↩
-
数学的には「$\alpha$ が $\beta$ の単数倍である」という関係は同値関係になっていることがわかります。 ↩
-
正確にはこの段階では既約元 ↩
-
そのような整数は必ず存在します ↩
-
行列式が $(a - b)(a - c)(a - d)(b - c)(b - d)(c - d)$(対称式) の形で書けることはすぐにわかるので、次数を合わせると自然にこの式が導かれます。 ↩