GLSL でのレイマーチングについて雑に語ってみます

第二次チョコレイマーチング大戦

先週、とんでもなく下らないネタを五日間に渡って投稿させていただきました doxas と申します。

詳細は以下です。

[連載 GLSL 物語] チカラが欲しいか……（第一話）

まあなんていうか、最後まで読んでくださった方は既にお気づきかと思いますが、オチを先に思いついて、それに向かってひたすらアホなことをやり続けた結果があの有様でありまして、反省も後悔もしてはおらんのですが、さすがにこのまま放置というのはいかんだろうと思い筆を執った次第です。

全てを漏れ無くというわけにはいきませんが、レイマーチングの基本の部分や、今回の一連の投稿において使われたテクニックなど、一部抜粋してご紹介します。

ただ今回紹介するテクニック等は基本的に単なるレイマーチングの話なので、より厳密にしっかりと数学的側面なども理解したいという場合は、あまり今回のテキストは向いていないかもしれません。奇しくも、週末にレイマーチングの基本を解説してくれている素晴らしいテキストが Qiita に投稿されていましたのでまじめに勉強したい方はそちらの記事を見ましょうね。

参考（同 AC 17日目の記事です）：[GLSL] レイマーチング入門 vol.1 - Qiita

私のほうは完全にネタが被ってることは理解してるんですが、上記引用記事が公開された段階で既にこの記事の原稿書いたあとだったのと、アプローチが全然違うのでまあいいかなっと自暴自棄になったのでそのまま公開します。 yay!

なお、左利きのきのこさんとたけのこ隊長がその後どうなったのか……

私にもわかりません。

（いまさらだけどモノホンのアポロってもっと尖ってたような気もする）

レイマーチング

レイマーチングについては、最近では結構日本語での情報をもチラホラと見受けられるようになってきまして、あらためてここで詳しく触れる必要はないかなと思うのですけれど、ハッキリ言って、数学が好きだとか、3DCG に多分に興味をお持ちであるとか、そういう素養を持ち合わせていないとどうしてもとっつきにくいと言いますか、要はプログラミングとしては結構難易度が高いものになっています。

とは言え、基本さえ押さえられてしまえば実は見た目ほどの謎技術というわけではなくて、単にベクトルでいろいろモミモミしているだけです。

たとえば、球体をレイマーチングで描くには、以下の式についてさえ理解できていれば十分です。

float f = length(ray) - rad;

なんのこっちゃ？

というみなさんの声は聞こえていますが聞こえていないことにします。

レイマーチングとは 距離関数 と呼ばれる関数を定義して、その関数が返す値を見ながら「レイがぶつかっているかどうか」を知る手法のことです。そして先ほどの式は、球体とぶつかっているかどうかの判断基準となる関数の中身です。

ここでのポイントは length という関数の使い方です。

GLSL のビルトイン関数である length は、与えられたベクトルの長さを返します。

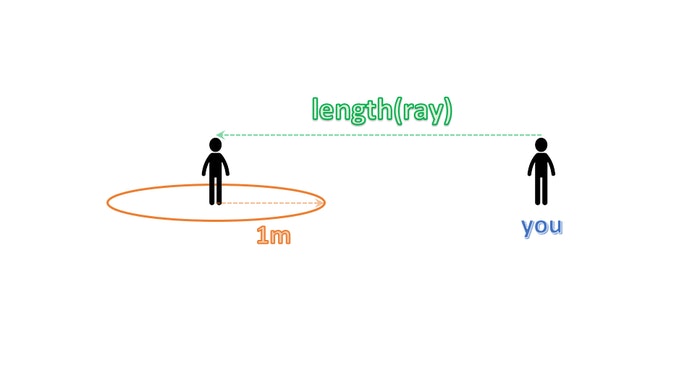
たとえば、あなたと、あなたの意中の人との間にある距離を ray だとすると、その距離を測ってくれるわけです。素晴らしいですね。

ただ問題なのは、あなたの意中の人は大変な人嫌いでして、常日頃から「私の半径 1m 以内になんぴとたりとも立ち入ることは許さん！」とかわけのわからないことを言っている、痛い人であるという点です。

困りましたね。

まあそのこと自体はどうでもよくて、上の図と、先ほどの式との関係をよくよく考えて見いだせるかどうかです。

もう一度、式を掲載してみます。

float f = length(ray) - rad;

はい、この式のなかの rad こそが、あなたの意中の人が言う「私の半径 1m」に相当します。

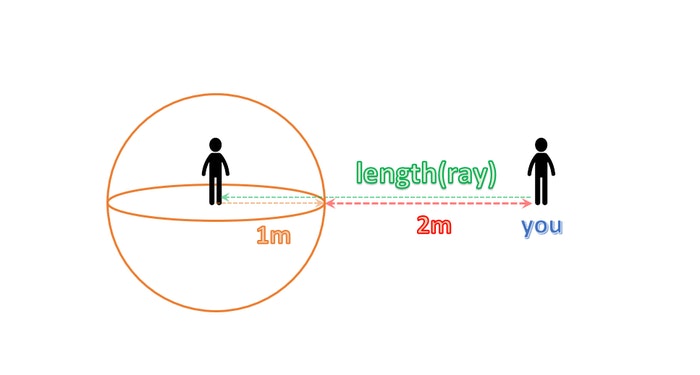
ここでは仮に、あなたとあなたの意中の人との間が 3m 開いていたと過程してみましょう。

すると、以下のような結果になります。

// 2.0m =     3.0m    - 1.0m
float f = length(ray) - rad;

意中のひとにギリギリまで近づきたい衝動をあなたが押さえきれない場合は、あと 2m は近づくことができるのがわかりますね。

それ以上踏み込んだらポイズンであることは、言うまでもありません。

さて、ここでは実社会に即した非常にわかりやすい例を使って説明しましたが、要は、これこそが距離関数です。

距離関数とは、ある座標から、対象となるオブジェクトまでの最短距離を返します。

ここでいうオブジェクトとは、意中の人が張っている「バリア」に相当しますね。

あなたの意中の人は、自分を中心に、円形にバリアを形成しています。距離関数にあなたが立っている座標を与えると、このバリアまでの最短距離を返してくれるわけです。一見、何を言っているのかよくわからないと思いますが、私も書いていてよくわからなくなってきました。

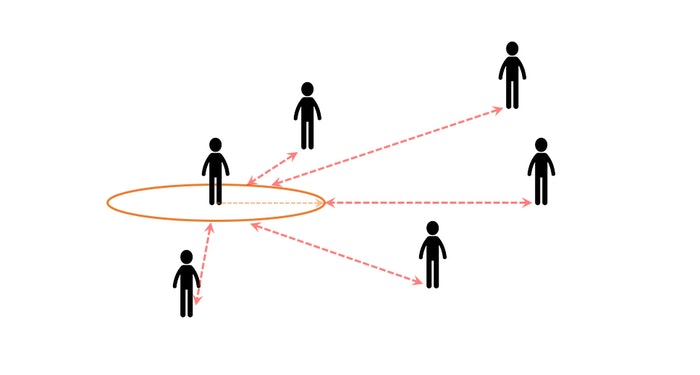
しかし以下の図のように、あなたが世界のどこに立っていようとも、あなたの意中の人との最短距離は、常にこの関数を用いるだけで知ることができます。

円や球は最もシンプルな形

さて、今回の例に示したように、円や、あるいは球というのは、距離関数で表現する上で最もシンプルな形状だと言えます。

なんてったって、半径を引けば、それだけで自然と円形のバリアができてしまうからです。これが仮に三次元の球体であっても、やはり球体は半径ひとつで表現できてしまう形状であり、考え方は円の場合と基本的になにも変わりません。

今回はわかりやすさ重視で書きましたが、要はこの場合の距離関数同様に、特定の形状を表すことが可能な距離関数を定義することができれば、それだけでレイマーチングを行うことができますし、逆に言えば、あらゆる形状の距離関数が定義できたとすれば、レイマーチングでどのような形状であれ表現できることになります。

ただし、オブジェクトの形状が特殊な場合や、複数のオブジェクトを同時に描かなければならない場合は、ちょっと工夫してやらないといけなくなります。

複数のオブジェクト

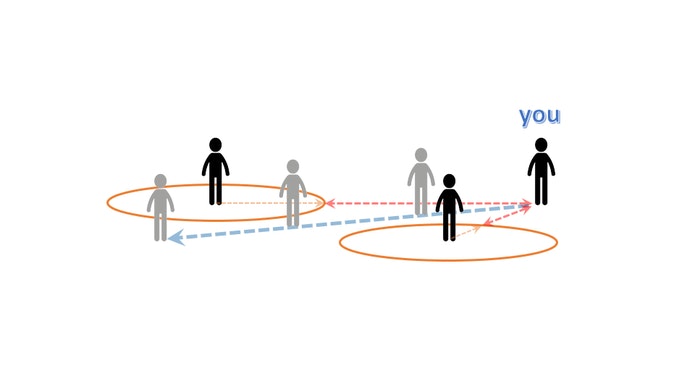
たとえばあなたの意中の人が複数いる場合を考えてみましょう。

二人目の意中の人は、人嫌いではありませんが極度の潔癖症であるために、やはりあなたを含む他人全てに対して半径 1m 以内への接近を拒むものとします。

さて困りました。

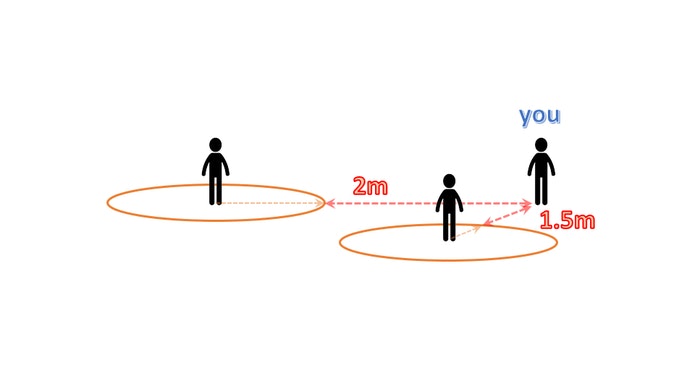
今度は、ふたりの想い人がいるというなんとも黒い構図です。

でも構図が黒いことが問題ではなく、ふたりの想い人に対して、それぞれ近づける距離に違いがあるというのが最大のポイントです。

今回のケースのように、複数のオブジェクトが存在する状況を考える上では、最も距離が短い相手との距離を進むことができる距離として考えます。冷静になって考えてみれば当然のことですが、たとえば一直線上に想い人が複数鎮座している場合には、当然一番近い人のところまでしか到達できませんね。ですから、複数のオブジェクトを同時に描く場合は、最も近くにあると思われるオブジェクトまでの距離を、最短距離として採用すればいいのです。

この原理がわかってさえいれば、複数のオブジェクトを同時にスクリーン上に出すことができます。

レイが進む方向

さて、このように距離関数が最短距離を測ってくれるものであること、また複数の結果を同時に扱う場合にはより小さい値を優先すればいいことがわかりました。

しかしここで、大問題があることが発覚してしまいます。

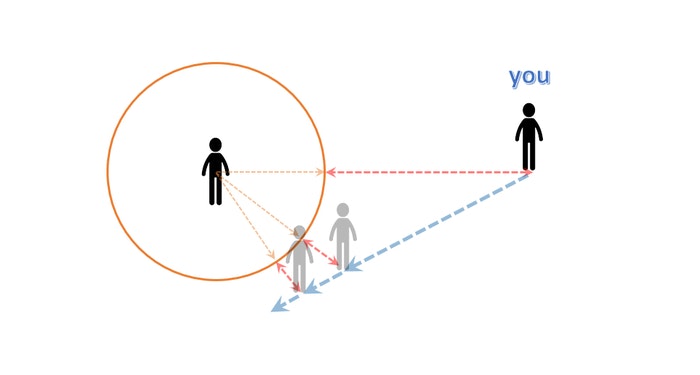
なんと、あなたは実は「決められた方向にしか歩くことができない病」という大変難儀な病気を患っていたのです。複数の想い人のうち、誰かが目の前に立っていたとしても、その方向に向かって歩いていけるかどうかはわかりません。たとえば以下のようなことが起こり得るわけです。

ああっ！

目の前にふたりも意中の人がいるにもかかわらず、あなたは自身の患っている「決められた方向にしか歩くことができない病」により、偶然にもバリアの間をすり抜けていってしまうというケースもあるわけです。レイマーチング的視点では、このようにどのオブジェクトにも衝突しなかった場合というのは当然存在するわけで、このような場合はレイが無限遠に飛んでいってしまったこととして扱います。

レイが進む距離

また、あなたはさらにもうひとつ、不治の病に罹っています。

それは「想い人までの最短距離分を一歩で進んでしまう病」です。

この病は非常に悲しい病でして、想い人の近くを通るときには地獄です。なぜなら、目の前に想い人がいるということは、当然そのあいだの距離は極めて小さいはずであり、その距離分を一歩で進んでしまうということは……

遠くにいる場合はたった一歩でたくさん進むことができるが、逆に近い距離にいる場合には、なかなか前に進むことができなくなってしまうからです。

これを見るとわかるとおり、距離関数によって返された最短距離分を、決められた方向にしか進むことができず、しかも一歩で、その最短距離分を進んでしまう。

これがあなたです。

やばいですね。

いますぐ病院に行ったほうがいいでしょう。

さりとて、このあたりまでくると、そろそろレイマーチングがどんな仕組みでグラフィックスを描いているのか、わかってきます。

ロジックをシェーダとして記述

ここまでの内容を簡単にまとめてみましょう。

• 距離関数はオブジェクトまでの最短距離を返す
• レイはこの最短距離分を進むことができる
• ただし方向転換はできない
• 距離関数の結果はより小さいもの（0 に近いもの）を採用する
• 距離関数の結果が極めて 0 に近い場合は衝突しているとみなす
• 最短距離を返すアルゴリズムが記述できればどのような形状でも表すことができる

レイマーチングを行っているコードを眺めると、一見して何が起こっているやら、わけがわからないことが多いと思います。

しかし実際には、上記に書き起こしたような計算を、何度も何度も繰り返し行うことによって、そこにオブジェクトが存在しているのかどうかを確かめているに過ぎません。

スクリーン上に描きたいオブジェクトの数だけ、距離関数を呼び出し、結果を比較しながら、最も近くにあるオブジェクトを探します。

そして、その求めた最短距離分だけ、レイを進める。

これを画面上の全てのピクセル上で繰り返し行なっていくわけです。当然、計算を行う量は膨大です。もし JavaScript でこのような計算を行ってしまったら、とんでもなく重いプログラムが出来上がるでしょう。しかしそこは、高速な GPU 上で動作する GLSL だからこその計算能力で、ゴリゴリと力押しで突き進んでいきます。

レイマーチングの作例としては、いくつか実装のスタンスというのがあると思いますが、今回のチョコレイマーチング大戦で登場した各種コードの場合は、カメラの座標を定義してやり、そこから三次元空間の前方に向かって、放射状にレイを飛ばしています。

たとえば以下のようなコード。

// 原点が中心となる二次元座標をまずは生成する
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);

// カメラの位置、向き、天面の向き
vec3 cPos = vec3(0.0,  0.0,  3.0);
vec3 cDir = vec3(0.0,  0.0, -1.0);
vec3 cUp  = vec3(0.0,  1.0,  0.0);

// 横方向を定義するベクトル
vec3 cSide = cross(cDir, cUp);

// フォーカスする深度
float targetDepth = 1.0;

// 上記パラメータから三次元のレイの情報を生成する
vec3 ray = normalize(cSide * p.x + cUp * p.y + cDir * targetDepth);

ここは単純に数学的な理解が求められる部分なので、コメントを読んでもいまいちわからんぞ？ という場合は、チョコレイマーチング大戦のコードを読み解くのは難しいかもしれません。でもまあ、別にいいんです。あとから興味出てきたら、調べればいいんです。兎角、これで「レイを定義する」というところまではできたのです。

あとは、レイを先ほどのあなた自身に見立てて、距離関数を呼び出していけばいいわけです。

マーチングループ

先ほど例に挙げたように、今しがた定義したレイは、一歩一歩、どのくらい進めるのかが毎回違います。一気に大きく前進できる場合もあれば、オブジェクトすれすれを通過するがために小さいレンジでしか進めない場合もあるでしょう。

また、一歩では届かなかったとしても、数十歩、あるいは数百歩進んだら、なにかにぶつかる場合だってあるかもしれません。

このようにレイマーチングでは、繰り返し繰り返し、何度もレイを進めていく作業を行う必要があり、これにはループ構文を使ったマーチングループを記述します。

たとえば、以下のような感じ。

// 距離関数の戻り値を格納するための変数
float dist = 0.0;

// レイが進んだ総距離
float rLen = 0.0;

// 今現在のレイの先端座標
vec3  rPos = cPos;

// マーチングループ（128回ループさせる場合）
for(int i = 0; i < 128; ++i){
    dist = distanceFunction(rPos);
    rLen += dist;
    rPos = cPos + ray * rLen;
}

距離関数が、すなわち上記で言うところの distanceFunction に相当します。こいつが、最短距離を測って返してくれるものとして考えてみましょう。

ループ構文のなかで、距離を測り、それを加算し、また距離を測り、それを加算し、を繰り返していくわけです。

最終的な衝突判定

最終的に、上記のマーチングループが終了したあとの状態で オブジェクトまでの最短距離が非常に小さい（0 に近い） 場合には、あなた（レイ）は想い人の張ったバリアにぶつかってポイズンしかけているはずですので、これを見てやれば衝突していると思われるのか、それとも明後日の方向に歩み去っていってしまったのかを知ることができます。

あとは、ぶつかっていたと思われる場合にだけ色を出力するロジックを変えてやれば、めでたくオブジェクトの形状がスクリーンに描き出されるでしょう。

つまるところレイマーチングとは、レイを、オブジェクトとの距離を計測しながらマーチング（行進）させていき、距離が非常に小さい場合に衝突とみなしている。

これが全てなわけです。

途中でも書いたように、レイがオブジェクトすれすれの場所を通る場合は、レイはなかなか前に進まなくなります。ですから、複雑なシーンであればあるほど、マーチングループの回数を増やしてやらないと、正しい描画結果にならない場合が多くなります。

チョコレイマーチング大戦のコードの多くでは、256 回とかマーチングループを回していますが、この数字に大きな意味があるわけではなく、単に切りの良い数字でしかも見た目が安定している回数を目測で設定しているだけです。

距離関数の書き方・考え方

さて、レイマーチングの基本は、要はおかしな性癖とおかしな病を患っているあなたのようなレイという仮想的存在を定義し、そいつを歩かせるだけだということがわかりましたね。

また、距離関数を工夫してやることで、様々な形状のバリアを張る想い人を定義でき、任意の形状を描き出すことができることもわかりました。

たとえば今回たびたび登場した、左利きのきのこの戦士は、どのような距離関数によって生み出されていたのでしょう。

該当するコードを見てみましょうね。

float smoothMin(float d1, float d2, float k){
    float h = exp(-k * d1) + exp(-k * d2);
    return -log(h) / k;
}
float dChoco(vec3 p){
    float rad = time * 0.2;
    mat3 m = mat3(cos(rad), 0.0, -sin(rad), 0.0, 1.0, 0.0, sin(rad), 0.0, cos(rad));
    vec3 q = m * (p + vec3(0.0, -0.55, 0.0)) * vec3(1.0, 1.2, 1.0);
    float len = sin(atan(q.z, q.x) * 7.0) * 0.01 * PI;
    return length(q) - 1.0 + len + step(p.y, -0.4) + pow(p.y, 1.0);
}
float dCylinder(vec3 p, vec2 r){
    float rad = time * 0.2;
    mat3 m = mat3(cos(rad), 0.0, -sin(rad), 0.0, 1.0, 0.0, sin(rad), 0.0, cos(rad));
    float s = -cos(p.y * 2.0) * 0.1 - 0.05;
    float l = length(p + vec3(0.0, 1.25, 0.0)) - 0.4;
    vec3 q = m * p + vec3(s, 0.5, 0.0);
    vec2 d = abs(vec2(length(q.xz), q.y)) - r;
    return smoothMin(min(max(d.x, d.y), 0.0), l, 32.0) + length(max(d, 0.0)) - 0.2;
}

まあコレ見せられて、なるほどなッ！ ってなる人は、頭のおかしい人だけだと思います。

ハッキリ言って私だってこれだけ見せられても、実際に実行してみなければようわからんです。

しかし距離関数を自分でもりもり書いていく場合には、いくつかポイントだけ押さえておけば、なんとかなります。

大事なことは既に書いたとおりですが、以下のようにまとめることができます。

• 各関数が受け取る引数 vec3 p にはレイの先端の座標が入っている
• 距離関数は「最短距離」を返す
• 距離関数の戻り値が 0 に近い場合に衝突になる

特に大事なのは、最後です。

衝突として判定されるのは、0 に極めて近い、小さな値が返された場合です。

このことをしっかり意識しましょう。

たとえばきのこの傘、これを距離関数で定義するにはどうしたらいいでしょうか。

きのこの傘が波打つ様子を距離関数に仕込むには

まず、きのこの傘は、オブジェクトというか、描こうとしている最終的な状態で言うと、上半分にしか実体がありませんね。

この上半分にしか実体がない、ということがまず最初のポイントです。

たとえば球を描く距離関数を思い出しながら考えてみましょう。

// rad は球の半径
return length(p) - rad;

こうでしたね。

んで、これが 0 に近かったら、衝突としてみなされるわけです。

ならば、下半分を消したいとすれば、超極端にわかりやすく書くと次のようにすればいいわけです。

float f = length(p) - rad;
if(p.y < 0.0){
    f += 100.0;
}
return f;

三次元空間の座標系は多くの場合、スクリーンの中央を原点に設定していますので、Y 座標が 0.0 より小さい座標とは、スクリーンの下半分、つまり Y 座標が負の値の座標ということになります。

つまり上記のような距離関数では、関数の戻り値が、レイの Y 座標が負の値である場合、極端に大きくなります。ですから、当然レイが衝突しているとはみなされなくなります。

キレイに下半分が消えました。

これで、きのこの傘のように、上半分にだけ実体のある状態は作れますね。

あとは、これを波打たせてやればきのこの傘っぽい感じになるでしょう。

じゃあどうやって波打たせるか……は、私が書いた GLSL で太陽っぽいものを描く にヒントがあります。

上記の記事のなかで、太陽から放出されるコロナを波打たせるような、アークタンジェントを使った処理を書いています。これを応用してやればいいのです。

より具体的には、レイの座標の XZ 座標を対象としてアークタンジェントを計算し、その結果からサイン波を作るわけです。ここで作られたサイン波は、きのこの傘を上から見ているような感じで考えると、ちょうど傘の中心から傘の縁までの距離が、波打つように変化する状態を作っていることと等しくなります。

上記引用記事では、サイン波の上下する値を太陽のコロナに見立てましたが、きのこの傘の波打つ様子に、同じようにこのサイン波を使ってやるわけですね。

さて、ここまでの前提を理解した上で、もう一度距離関数の例を書いてみると以下のようになります。

float f = length(p) - 1.0;
float t = sin(atan(p.z, p.x) * 6.28) * 0.1;
if(p.y < 0.0){
    f += 100.0;
}
return f + t;

はい、なんかそれっぽくなりましたね。

軸の部分はシリンダー

日本語で円柱を表す「シリンダー」を使って、きのこの軸の部分を描きます。

先ほど掲載した実際に使った距離関数はコードの量がそれなりに多いように見えたかと思いますが、実はシリンダーを描くための最低限のコードならそれほど量は多くありません。

float dCylinder(vec3 p, vec2 r){
    float rad = time * 0.2;
    mat3 m = mat3(cos(rad), 0.0, -sin(rad), 0.0, 1.0, 0.0, sin(rad), 0.0, cos(rad));
    float s = -cos(p.y * 2.0) * 0.1 - 0.05;
    float l = length(p + vec3(0.0, 1.25, 0.0)) - 0.4;
    vec3 q = m * p + vec3(s, 0.5, 0.0);
    vec2 d = abs(vec2(length(q.xz), q.y)) - r;
    return smoothMin(min(max(d.x, d.y), 0.0), l, 32.0) + length(max(d, 0.0)) - 0.2;
}

まあこれ全体を見せられたらマジ意味わからんわコレ状態だと思いますが、最初のほうは、実は全体を回転させたりするために行列を定義したりしているところなので、直接的にシリンダー生成を行うのに関連しているのは一部だけです。

ここでは細かく分解して見てみましょう。

まず既にお気づきの方もいらっしゃるかもしれませんが、GLSL のビルトイン関数ではない怪しげな関数が呼ばれているところがあります。

それが smoothMin です。

これは名称的にいかにも私ビルトイン関数よウッフンしてますが、違います。

それを踏まえ、いろいろいらんもんを削除してスリム化してみると次のような感じになりますね。

float dCylinder(vec3 p, vec2 r){
    vec2 d = abs(vec2(length(p.xz), p.y)) - r;
    return min(max(d.x, d.y), 0.0) + length(max(d, 0.0)) - 0.1;
}

一気に行数が少なくなりましたね。

通常、シンプルな形状を表現するための距離関数はこのように極めてシンプルです。そこに、回転や変形を加えていったり、あるいは結合を行なったりするので、得てして行数が増えていくだけです。まず最初は、こういったシンプルな状態からスタートするのがわかりやすいと思います。

じゃあどうしてこれで円柱がレイマーチングによって描き出せるのか……

それは、ここまで繰り返してきたレイマーチングの基本を思い出しながら考えていきましょう。

まあたとえばの話、上のコードの中の、戻り値を返却している行。そこの末尾にある 0.1 を変化させるとどんなことが起こると思いますか？

float dCylinder(vec3 p, vec2 r){
    vec2 d = abs(vec2(length(p.xz), p.y)) - r;
    return min(max(d.x, d.y), 0.0) + length(max(d, 0.0)) - 0.1; // ← こいつ
}

レイマーチングでは、距離関数の返す値が 0 に極めて近い場合がポイズンでしたよね。

そのことをもう一度思い出しながら考えましょう。

先ほどのコードはベクトルやら minmax やらいろいろ出てきてはいますが、俯瞰的に見てみると次のように戻り値を返しています。

return なんか + なんか - 0.1;

なんかとなんかを足して、そこから 0.1 を引いている感じですね。ということは、単に足したり引いてるしているだけであることがわかります。つまり最後の 0.1 を増やしたり減らしたりすると、単純に戻り値が大きくなったり小さくなったりすることがわかります。

それでは実際に、この 0.1 の部分を 0.3 とかにしてみましょう。

するとこうなります。

さあどうでしょうか。

レイマーチングがだんだんわかってきましたか？

戻り値を返却する際に行う減算処理で、より多くの数値を減算する。それはつまり、物体がより大きく膨らんでいくことを表します。なぜなら、戻り値が小さく、より 0 に近い場合をレイマーチングでは衝突とみなすからです。

これまでは若干距離が足らなくて想い人のそばを泣く泣く通り過ぎていたレイであっても、戻り値の値が減算されると、ポイズンする可能性がより広がるわけです。

頭で考えるときに、減算というと小さくなるようなイメージをどうしてもしてしまいます。しかしレイマーチングの世界では減算はむしろオブジェクトを大きく膨らませる効果があるのですね。

複数のオブジェクトと色

途中でも書いたことですが、レイマーチングでは複数の形状を同時に描画することができます。

単にきのこの傘と軸、このふたつを同居させるだけのコードを見ながら考えてみますかね。

float dChoco(vec3 p){
    float f = length(p) - 1.0;
    float t = sin(atan(p.z, p.x) * 6.28) * 0.1;
    if(p.y < 0.0){
        f += 100.0;
    }
    return f + t;
}
float dCylinder(vec3 p, vec2 r){
    vec2 d = abs(vec2(length(p.xz), p.y)) - r;
    return min(max(d.x, d.y), 0.0) + length(max(d, 0.0)) - 0.3;
}
Intersect distanceHub(vec3 p){
    float choco = dChoco(p);
    float cylin = dCylinder(p, vec2(0.1, 0.9));
    Intersect i;
    i.dist = min(choco, cylin);
    i.color = cylin < choco ? kColor : cColor;
    return i;
}

上記のコードは、解説するのに使ったきのこの傘と、軸の、両方のコードが含まれています。

dChoco が傘を表す距離関数。そして dCylinder が軸です。

さらにもうひとつ distanceHub という関数があるのがわかりますね。これが複数の異なる形状を同時に描くのに一役買っています。

ここでの考え方も、既に解説したとおり、レイマーチングの考え方の基本が大事です。レイマーチングで複数のオブジェクトを同時に描きたい状態というのは、想い人が複数いる状態の黒いあなたを想像します。そのときはどうすればよかったんでしたっけね。

複数のオブジェクトを描く場合には、戻り値として、距離関数の結果が小さい（0 に近い）ほうを採用すればよかったんでしたね。

関数 distanceHub はまさにそれを行っている関数です。自身のなかで描きたい形状の距離関数を呼び出し結果を取得したあと、その結果に応じて処理を行ってくれるいわば距離関数のハブのような役割を担っています。よーく見てみると Intersect.dist に対して min 関数を使った値を格納しているのがわかると思います。より小さい値のほうを、戻り値に採用しているわけですね。

実は色を塗り分けるのも、同じ理屈でやっているんですよ。

同様に Intersect.color に対して、距離関数の結果如何によって異なる色が代入されるように書かれているのがわかりますね。

さあもうここまでくれば、あとはこれらをさらにモミモミと揉みしだいていけばいいだけです。

一連の連載記事では、きのこやたけのこの戦士、あるいはアポロを模した太陽神などが登場しましたが、よく考えてみたらポッキーナベイベであればシリンダーひとつで色を適当に Y 軸にアタッチするだけで描けますね。やばいですね。

まとめ

さて、レイマーチングについて簡単に解説してみました。

これまでにも、何度かレイマーチングについて解説する機会がありましたが、毎回毎回、どういうふうに説明するのが一番理解を得られるのだろうかと、考えさせられます。

もともと数学の素養がある方や、普段から 3D になにかしらの形で関わっている人であれば、それほど難しいことをしているわけではないのがわかると思います。ただどうしても、ベクトルとか、三次元数学とか、そういうことに関する慣れが無い場合は、難しいと感じてしまう部分が多かったかもしれません。

私の体感というか、むしろ経験則になってしまいますが、WebGL や GLSL、あるいは 3D 表現に初めて挑戦する多くのプログラマが、二次元的な座標はイメージできても、三次元的座標を直感的に理解できない（思い描けない）場合が多いように感じます。我々は普段、現実世界という三次元の世界に生きているにもかかわらず、次元がひとつ増えただけで頭のなかがこんがらがってしまうんですね。

それに、WebGL に限ったことではないのですが、3D 系のプログラミングでは一度に覚えなくてはならないことが異常に多いです。

3D API のお作法から、シェーダの記述方法から、慣れない三次元をイメージしながらいきなり全てをこなしていくのはなかなかの苦難に満ちた道のりです。

ですから個人的には、はじめはツールを活用したり、あるいは既に転がっているサンプルを転用したりしながら、できるかぎり細切れに勉強していくべきだと思います。GLSL はシェーダという概念を理解するうえでは取っ掛かりとして優れたテーマであると思いますが、そこをあえてさらに細切れにし、まずは「GLSL でフラグメントシェーダを書く」というところにフォーカスし、慣れていくのもひとつの方法だと思います。

今回のアドベントカレンダーではいろいろなことを言ったりやったりしましたが、少なくとも私個人のなかでは GLSL は怖くない （少なくとも最初のうちは……）ということをお伝えしたかったということに終始していました。高度なことをしようと思えば、当然難易度は跳ね上がっていくものですし、それは何事においてもそうでしょう。でも、シェーダや GLSL という概念は、要はどのように付き合っていくのかが大事なだけで、けして門戸が開かれていない「一部の天才たちのためだけの玩具」ではないのです。

このテキストでは、そもそも GLSL とはどういうものであるとか、フラグメントシェーダがどういうものであるとか、そういったところの説明はかなり省いてしまっています。もしもシェーダや GLSL という概念に少しでも興味が沸いたのなら、まずは今年のアドベントカレンダーの中から、気になるものをピックアップしてご覧になってみてはいかがでしょうか。

ちょっと長い文章になってしまいましたが、最後まで読んでいただけて、うれしいです。

ありがとうございます。