シェーダ書きたくてしょうがないマン! 
GLSL で暖を取りたいみなさまこんばんは。🔥🔥🔥
世の中にはたくさんの シェーダ書きたくてしょうがないマン が居るはずなんですが、身分を明かすことにより悪の組織から生命を狙われる可能性がある彼らはおいそれと Advent Calendar に投稿することもままなりません。悲しいですね。
そこで、一般市民として平々凡々に生活している私が代わりに、GLSL で世の中の GPU の温度を一度でも温められるようにがんばらなくてはと一念発起いたしました。
GLSL ワークショップ 
先日、GLSL のワークショップを開催しました。そこではたくさんのシェーダ作品が投稿され、まさに 隠れシェーダ書きたくてしょうがないマン や、有望な 新人シェーダ書きたくてしょうがないマン を発掘することができました。ありがとうございました。
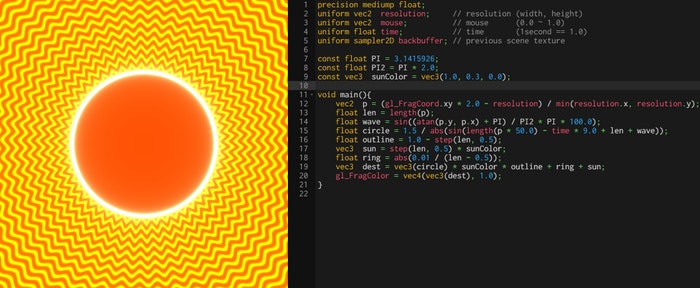
そんなワークショップで私が投稿した「真夏の太陽」について、ちょっとした解説を書いてみようかなと思います。
基本的にはあまり難しいことをしているわけではないので、これをご覧のみなさんもぜひオリジナルシェーダの記述にトライしてみてください。
GLSL Editor 
GLSL でシェーダを書くためには、glslsandbox などの有用なサイトが既にいくつかあります。
今回は、私の作ったオンライン GLSL Editor を使いましょう。
どうしても glslsandbox などの場合、実行を止めたりできない都合から、マシンに負荷が掛かりすぎてしまう傾向があります。それはそれで GPU がほっかほかでイイ感じなのですが、マシンが壊れてしまっては元も子もないですよね。
GLSL Editor では、512px 四方のそれほど高負荷にならない広さの描画エリアと、Esc キーによる任意タイミングでの実行停止が行えますので、あまり高負荷になりすぎないように注意しながらシェーダを記述できますので、ぜひ利用してみてください。
真夏の太陽 
まず、今回のシェーダですが、ソースコードは以下のようになっています。
precision mediump float;
uniform vec2 resolution; // resolution (width, height)
uniform vec2 mouse; // mouse (0.0 ~ 1.0)
uniform float time; // time (1second == 1.0)
uniform sampler2D backbuffer; // previous scene texture
const float PI = 3.1415926;
const float PI2 = PI * 2.0;
const vec3 sunColor = vec3(1.0, 0.3, 0.0);
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
float len = length(p);
float wave = sin((atan(p.y, p.x) + PI) / PI2 * PI * 100.0);
float circle = 1.5 / abs(sin(length(p * 50.0) - time * 9.0 + len + wave));
float outline = 1.0 - step(len, 0.5);
vec3 sun = step(len, 0.5) * sunColor;
float ring = abs(0.01 / (len - 0.5));
vec3 dest = vec3(circle) * sunColor * outline + ring + sun;
gl_FragColor = vec4(vec3(dest), 1.0);
}
こうして見てみると結構な行数がありますね。
でもまあ、これくらいの行数のシェーダであれば、概ね負荷もそれほど高くない場合が多いです。GPU で目玉焼きを作りたい人出ない限りは、それほどがっかりする必要はありませんよ!
これを先ほどの GLSL Editor に貼り付けて、Ctrl + s か、もしくは Command + s してみましょう。
すると、以下のような描画結果になると思います。
GLSL を記述していく上で大切なことは、一気に全体を把握しようとするのではなく、できる限り、細切れにソースコードの意味を読み解いていくことです。
今回のシェーダの場合、GLSL ワークショップ当日に書いていた最中よりも、変数の意味などをわかりやすく置き換えしてありますので、各行ごとに、どのような効果を狙って書かれたものであるのかを、焦らず把握していきましょう。
座標系の正規化 
さて、ここはもうおなじみなのでサラッと行きたいところです。
スクリーンの解像度を示す uniform 変数である resolution と、処理対象ピクセルの座標を取得する gl_FragCoord を使って、画面の中心部分に原点が来るように座標を正規化することから全てが始まります。
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
ここで割る方の値に min を使っているのは、スクリーンが仮に正方形ではなく長方形であった場合にも対応するためです。
ベクトルの長さを測る 
さて、次の行では、今しがた正規化したばかりのベクトルちゃんを lenght 関数に与えて長さを測っています。
こうすることで、画面の中心から、処理しようとしているピクセルまでの距離がわかるんですね。
これは単体でそのまま可視化に使われるわけではないのですが、全体の波紋のような模様を作るのにも、太陽のシルエットを描くのにも使われている大事な係数になります。
float len = length(p);
波紋模様を作る 
続いては太陽から放出されている波紋模様です。
ここは、先ほど測ったベクトルちゃんの長さをうまく利用します。
まず、ベクトルの長さを何倍かに伸ばした上で、それを sin に与えるとどういう絵が出るのか、考えてみましょう。
コードで書くなら、次のような感じです。
float circle = sin(length(p) * 100.0);
これをそのまま RGB に色として出力すると、こんな感じの見た目になりますよ!
これは、ベクトルの長さを 100 倍して大きく伸ばしたあと、それをサイン波に変換することによって描くことができる模様ですね。
これに時間の経過の影響を加えてやれば、それだけでサークル模様が外側や内側に向かってアニメーションするような状態にすることもできます。
今回の「真夏の太陽」の場合は、これを変形することで、太陽の外側の波紋模様を描いているんですね。
float circle = sin(length(p) * 100.0 - time * 9.0);
波紋をギザギザに波打たせる 
さて次はちょっと頭を柔らかくして考える必要がありますよ!
波紋をギザギザにしてやり、太陽からコロナが吹き出しているかのようにしていきます。
実は、これにもやっぱりサイン波を使います。
まず、アークタンジェントを使って、円形に値が徐々に大きくなっていく状態 を作るところからスタートしましょう。アークタンジェントを使うとどうして円形に値が大きくなっていく状態を作れるのかは、適当にググろうね!
float arctan = (atan(p.y, p.x) + PI) / PI2;
上記の PI は、パイ、つまり円周率を表していて、PI2 はその倍です。
これをそのまま RGB に突っ込んで表示すると、以下のような感じになります。
さて、どうでしょう。
見事に、左端の水平線から、円形に徐々に値が大きくなっていっているのがわかりますね。値が徐々に大きくなっていくということは、これをまた何倍かに大きくしてやって、それをサイン波に突っ込んでやると、やっぱり値が激しく上下するような、そんな状態を作ることができるんですね。
完成した GLSL のコードで言うと、変数 wave に代入しているところで、これに相当する処理を行っていますね。
float wave = sin((atan(p.y, p.x) + PI) / PI2 * PI * 100.0);
太陽のアウトライン 
さて、次は太陽のアウトラインです。
太陽のシルエットを出すには、画面の中心から一定の距離までは…… という条件を満たすような状況を作ってやればいいですね。
これにはいろいろやり方があるかと思いますが、今回は step 関数を使っていますよ!
step 関数については、今回の Advent Calendar の 2 日目の記事で @yuichiroharaiJP さんが大変わかりやすい解説を書いてくれていますね。
参考: 条件分岐のためにstep関数を使う時の考え方をまとめてみた - Qiita
この step 関数を使って、中心からの距離が 0.5 までの部分と、それ以外の部分との間で処理が別れるようにうまくシェーダを書いてやります。
該当する箇所は、以下の部分です。
float outline = 1.0 - step(len, 0.5);
vec3 sun = step(len, 0.5) * sunColor;
リングを乗せて境界を誤魔化し+光らせる 
さてあとは、太陽のシルエットの境界部分に、リングのような光の輪っかを乗せてやればキレイに見えるようになるはずです。
リング上の光の帯を作るには、これにもやっぱり中心からの距離を見ながら処理してやる必要がありますね。最初に座標を正規化して length で測るような計算をしましたが、今回のデモの場合はこれが大活躍しているのがわかると思います。
float ring = abs(0.01 / (len - 0.5));
リングを出す際に、もしさらに太いラインで描画したければ、割られている数である 0.01 の値を変更してみるといいでしょう。
どうしてこのような計算で明るいリング状の光の輪ができるのかは……
単純な数学だから考えてみようね!
ちなみに、先ほどの太陽のシルエットに、リングを重ねた状態が次のような感じになります。
超合体させる 
さて、ここまで解説してきたようなテクニックをひとつひとつ組み合わせていくと、冒頭にも記載したシェーダのコードが出来上がります。
ドカッと全文を一気に見せられるとちょっと行数が多いように感じるかもしれませんが、ひとつひとつを細かく見ていくと、それぞれはそれほど難しいことをしているわけではないのですね。
こういったシェーダのコードを記述するときや、あるいは 3DCG の計算を頭のなかで構築する場合なんかもそうですが、混乱しそうになったらメモを取ってみたり、図形を書いて考えてみたりするのがおすすめです。
ちょっと意外に思うかもしれませんが、私も机のそばには手の届くところにメモ帳が置いてあります。これはとっさに連絡先をメモるためではなくて、とっさに図解して頭のなかを整理するために使っています。図を書かなくちゃわからないなんて恥ずかしいとか、そんなことを思う必要はありません。大抵の場合、ほとんどの計算は単純なもので十分なんです。しかしそれらが幾重にも絡まってくると、ちょっと一瞬では答えが浮かばない場合だって当然でてきます。
そういうときは、無理せず図解しながら考えてみましょう。
きっと、スッキリシャッキリ理解できると思いますよ。
最後にもう一度、シェーダのコード全文を載せておきます。
GLSL Editor に実際にコードを貼り付けて、そこでリアルタイムに編集しながら、挙動の変化を楽しんでみるというのも、シェーダの学習の助けになると思います。
ぜひ気軽にトライしてみましょう。
precision mediump float;
uniform vec2 resolution; // resolution (width, height)
uniform vec2 mouse; // mouse (0.0 ~ 1.0)
uniform float time; // time (1second == 1.0)
uniform sampler2D backbuffer; // previous scene texture
const float PI = 3.1415926;
const float PI2 = PI * 2.0;
const vec3 sunColor = vec3(1.0, 0.3, 0.0);
void main(){
vec2 p = (gl_FragCoord.xy * 2.0 - resolution) / min(resolution.x, resolution.y);
float len = length(p);
float wave = sin((atan(p.y, p.x) + PI) / PI2 * PI * 100.0);
float circle = 1.5 / abs(sin(length(p * 50.0) - time * 9.0 + len + wave));
float outline = 1.0 - step(len, 0.5);
vec3 sun = step(len, 0.5) * sunColor;
float ring = abs(0.01 / (len - 0.5));
vec3 dest = vec3(circle) * sunColor * outline + ring + sun;
gl_FragColor = vec4(vec3(dest), 1.0);
}
これであなたも今日から悪の組織に生命を狙われるかもしれません ![]()
そこは自己責任でお願いします!!!
Yay!!! ![]()
![]()
![]()
![]()
![]()