競プロで見るKőnigの定理

概要

二部グラフ上での最小頂点被覆のサイズが最大マッチングのサイズと等しいというのがKőnig(ケーニヒ)の定理です．
https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_%28graph_theory%29

具体的な問題を通してこの定理に触れたいと思います．

問題

USACOのAsteroidsという問題を例にして考えます．
http://poj.org/problem?id=3041
https://www.acmicpc.net/problem/1867

問題概要

N×Nマスのグリッド(1 ≦ N ≦ 500)があり，その上にK個の石(1 ≦ K ≦ 10,000)があります．
あなたは一回の操作で行または列を一つ選び，その行または列に存在する石をすべて取り除くことができます．
すべての石を取り除くための最小の操作回数を求めてください．

具体例

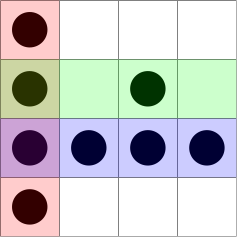
Xを石のあるマス，.を空きマスとし，以下のような状態を考えます．

X...
X.X.
XXXX
X...

このケースだと，以下のように行と列を選択することで最小回数を達成できます．

二部グラフ

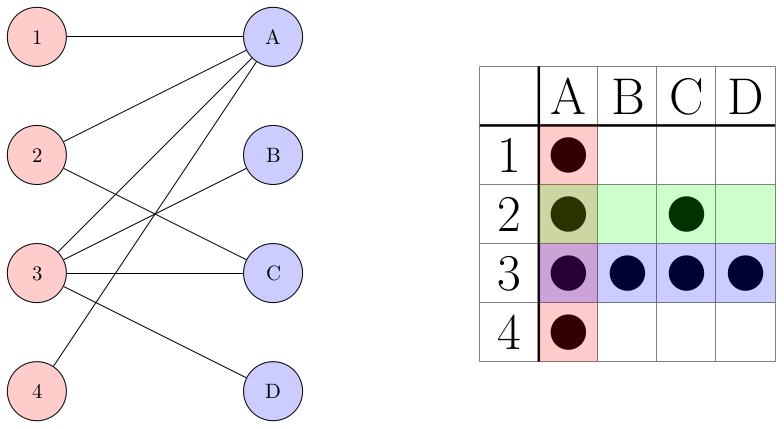
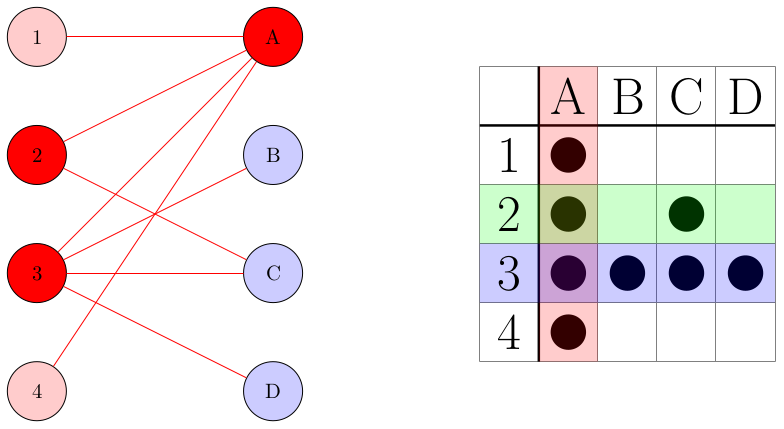
ここで，行を上から1, 2, 3, 4，列を左からA, B, C, Dと名前を付けます．
そして行と列を頂点に，石を辺に置き換えたグラフを作ります(例えば，左上の石は(1, A)にあるので1 - Aを結びます)．
これは二部グラフとなっています．

頂点被覆

グラフからいくつかの頂点を選択した集合をVとすると，すべての辺の両端のどちらかがVに含まれる場合，Vは頂点被覆であるといいます．
「選んだ頂点から出ている辺を塗り，すべての辺を塗れているかどうか」というイメージです．

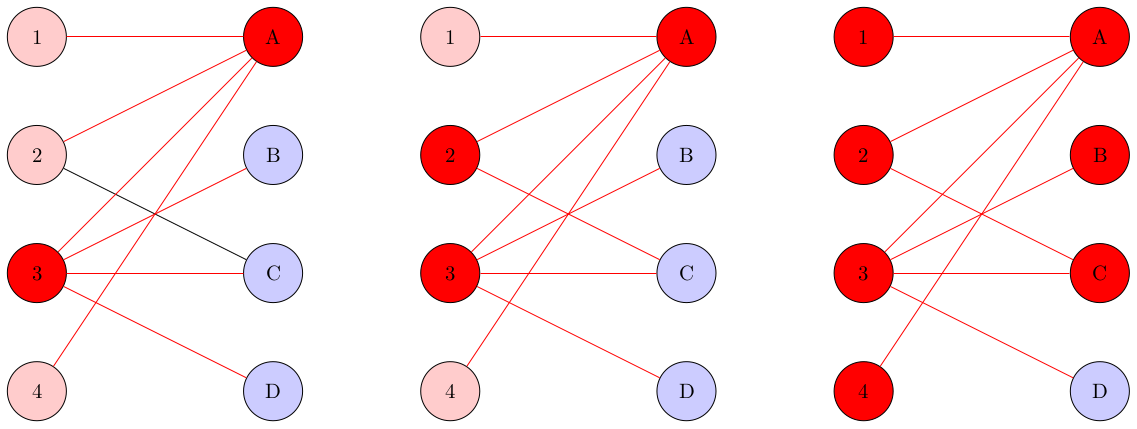
具体例を通して見てみましょう．

左のものは頂点{3, A}を選びましたが，(2, C)の辺をカバーしていません．
これは頂点被覆ではありません．

真ん中のものは頂点{2, 3, A}を選び，すべての辺をカバーしています．
そして，これが頂点数最小であり，最小の頂点被覆を最小頂点被覆と呼びます．唯一ではなく，例えば{3, A, C}を選んだ場合でも最小頂点被覆となります．

右のものは頂点{1, 2, 3, 4, A, B, C}を選び，すべての辺をカバーしています．
頂点被覆ではありますが，最小ではありません．

問題との対応

このグラフの導入は唐突に思えますが，問題との対応を見てみましょう．

操作として，行か列を選択するというのは頂点を選択することと対応し，そのライン上の石を取り除くというのはその頂点から出ている辺を塗るということに対応づきます．

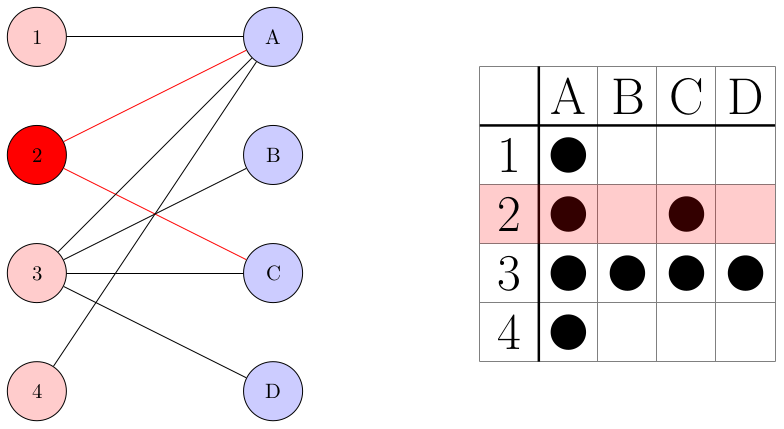
例えば，
2行目を選択する -> 頂点2を選択する
石(2, A)と(2, C)が除去される -> 辺(2, A)と(2, C)が塗られる
ことと対応します．

その上で，すべての石を取り除くというのはすべての辺を塗ることと対応し，操作回数の最小化というのは選択した頂点数の最小化に対応づきます．

これでこの問題を最小頂点被覆問題に帰着させることができました．

Kőnigの定理

Kőnigの定理により，二部グラフ上での最小頂点被覆のサイズと最大マッチングのサイズが等しいことが言えます．

具体的な証明は以下を参照してください．とても分かりやすくまとまっています．

競プロで使う Dilworth の定理
二部グラフの最小点被覆、最大安定集合 (最大独立集合)、最小辺被覆を総整理！
Kőnig の定理と最大流最小カット定理

一般のグラフでの最小頂点被覆問題はNP-hardのようです．¹

提出

二部グラフでの最大マッチングは最大流で解けます．詳しくは以下を参照してください．
‪実世界で超頻出！二部マッチング (輸送問題、ネットワークフロー問題）の解法を総整理！‬

最終的に最大流問題に帰着することができました．以下が提出コードです．
https://www.acmicpc.net/source/86519044

提出コード

#include <bits/stdc++.h>
using namespace std;

template<typename flow_t>
struct Dinic{
    struct Edge{
        int from, to, rev;
        flow_t cap;
        bool is_rev;
        Edge(int f, int t, int r, flow_t c, bool b) : from(f), to(t), rev(r), cap(c), is_rev(b) {}
    };

    vector<vector<Edge>> G;
    vector<int> dist;
    vector<int> iter;
    const flow_t INF = numeric_limits<flow_t>::max();

    Dinic(int N) : G(N), dist(N), iter(N) {}

    void add_edge(int from, int to, flow_t cap) {
        int fromrev = G[from].size();
        int torev = G[to].size();
        G[from].push_back(Edge(from, to, torev, cap, 0));
        G[to].push_back(Edge(to, from, fromrev, 0, 1));
    }

    void bfs(int s) {
        fill(dist.begin(), dist.end(), -1);
        dist[s] = 0;
        queue<int> q;
        q.push(s);
        while(q.size()) {
            int v = q.front(); q.pop();
            for(const Edge& e: G[v]) {
                if(e.cap == 0 || dist[e.to] >= 0) continue;
                dist[e.to] = dist[v] + 1;
                q.push(e.to);
            }
        }
    }

    flow_t dfs(int v, int t, flow_t f) {
        if(v == t) return f;
        if(f == 0) return 0;

        for(int& i = iter[v]; i < (int)G[v].size(); i++) {
            Edge& e = G[v][i];
            if(e.cap == 0 || dist[v] >= dist[e.to]) continue;
            flow_t flow = dfs(e.to, t, min(f, e.cap));
            if(flow == 0) continue;

            e.cap -= flow;
            G[e.to][e.rev].cap += flow;

            return flow;
        }
        return 0;
    }

    flow_t max_flow(int s, int t) {
        flow_t ret = 0;

        while(true) {
            bfs(s);
            if(dist[t] < 0) return ret;

            fill(iter.begin(), iter.end(), 0);
            while(true) {
                flow_t flow = dfs(s, t, INF);
                if(flow == 0) break;
                ret += flow;
            }
        }

        return 0;
    }

    vector<Edge> edges() {
        vector<Edge> ret;
        for(const auto& v : G) {
            for(const auto& e : v) {
                if(e.is_rev) continue;
                ret.push_back(e);
            }
        }
        return ret;
    }

    void debug() {
        for(const auto& v : G) {
            for(const auto& e : v) {
                if(e.is_rev) continue;
                cerr << e.from << " -> " << e.to << " (flow : " << G[e.to][e.rev].cap << " / "
                    << e.cap + G[e.to][e.rev].cap << ")" << endl;
            }
        }
    }
};


int main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    int N, K;
    cin >> N >> K;

    Dinic<int> dinic(2 * N + 2);
    int s = 2 * N, t = 2 * N + 1;
    
    for(int i = 0; i < K; i++) {
        int a, b;
        cin >> a >> b;
        a--; b--;
        dinic.add_edge(a, N + b, 1);
    }

    for(int i = 0; i < N; i++) {
        dinic.add_edge(s, i, 1);
        dinic.add_edge(N + i, t, 1);
    }

    cout << dinic.max_flow(s, t) << "\n";

    return 0;
}

類題

https://atcoder.jp/contests/abc274/tasks/abc274_g
https://yukicoder.me/problems/no/1479

最後に

Kőnigの定理について問題を通して紹介しました．

何かあればご連絡ください．

参考

https://codeforces.com/blog/entry/105697
https://en.wikipedia.org/wiki/K%C5%91nig%27s_theorem_%28graph_theory%29
https://byeo.tistory.com/entry/boj1867-%EB%8F%8C%EB%A7%B9%EC%9D%B4-%EC%A0%9C%EA%B1%B0

1. https://www.slideshare.net/wata_orz/ss-12131479 ↩