記事の要約
- 最終ゴールは、昨日作成した MVS (Multi View Stereo) のデプスマップのノイズ除去を行うこと。
- 具体的には、 P+P (Plane-Plus-Parallax) と呼ばれる手法を応用して再度デプスマップを作成し、MVS のデプスマップから共通する値のみ抽出する。
- 本記事では P+P とそれを応用したデプスマップの作成方法を概観し、それを Python3.7 で実装する。
こんにちは。サービスイノベーション部1年目社員の @dosada です。昨日の記事(できる!マネキンチャレンジデータセット(SfM・MVS編)) に続き @ohashi_zaemon とマネキンチャレンジデータセットを作っていこうと思います。
昨日の記事では Mannequin Challenge Dataset の概要と COLMAP を使ったデプスマップ作成の手続きが説明されました。ネット上のコンテンツを使い、単眼深度推定のための学習データを効率よく作成するために、 SfM (Structure from Motion) と MVS (Multi View Stereo) を行いました。実際の論文ではより効率的に処理をすすめるために SLAM を組み合わせることなども行われています。
今日の内容はノイズ除去。ただし P+P という聞きなれない手法が出てきたり深層学習でオプティカルフローを求めたり、そもそも実装が公開されていないから自分でコードを書いたりと、元データを作る以上に深い内容となっています。早速見ていきましょう。
Mannequin Challenge Dataset のノイズ除去
ノイズ除去 前半
気づいている方もおられるかもしれませんが、ノイズ除去の前半の内容は昨日の記事の最後の部分に登場していま す。論文中で
We first refine and filter depth outliers using the depth refinement method of [19].
という わずか一行 で片付けられてしまっていた、あの内容です。実装を後回しにしていた結果、このAdvent Calendar執筆の締め切り直前に内容を確認して見事に爆死しました。
幸い今回選んだ動画は、昨日までで完成したデプスマップを見てもそこまでノイズが多いわけではありません(というよりもそういう動画を 選ばざるを得ませんでした 選びました)。なのでこのプロセスはパスしても問題なさそうな気が...しています。
ノイズ除去 後半
ノイズ除去後半の内容は、一言で言うと「MVSとは異なる手法で再度デプスマップを作成し、両方とも同じ値が得られた部分のみ信頼できるデータとする」というものです。その「MVSとは異なる手法」は P+P (Plane-Plus-Parallax) と呼ばれるものになります。
Mannequin Challenge Dataset の論文は GitHub でソースが公開されているように表向きにはなっていますが、この P+P まわりの部分は公開されていません。どうやらロバストな実装が難しいことが理由らしいです。ちょっと面倒ですが、自力で実装していくしかないようです。
準備1: P+Pとは
P+P でデプスマップを作れと言われても、そもそも P+P が何者なのかわからないと実装しようがありません(筆者は聞いたことがこれまで聞いたことがありませんでした)。なのでまずは P+P を理解します。 Mannequin Challenge の論文にも引用されている P+P の論文の著者 Michal Irani 氏の講義模様が YouTube にアップロードされている(さらに内容もわかりやすい)ので今回はこの動画と、 Michal Irani 氏の論文を参考にまとめました。
ちなみにですが、この動画によると P+Pは90年代に論文がそれなりに書かれたものの、最近ではほとんど名前を聞かなくなった古典的な手法らしいです。その影響なのか、日本語による関連文献は今の所見つかっていません。
ホモグラフィーを3次元空間に適用させる
P+P を直感的に理解するために、ここでホモグラフィーの実験をしてみます。
ホモグラフィーとは、平面を線形変換を用いて別の平面に射影する手法で、二次元画像の変形などに使われています。スマホで書類のスキャンをするときなどで利用された方も多いのではないでしょうか?
斜めから撮影したスザーニもこの通り真上から見たような写真に。
このホモグラフィーは、特定の平面に対して綺麗に変形できますが、その平面以外については必ずしも綺麗に変形できるとは限りません。これはホモグラフィーが線形変換であることが元にあります。
綺麗に変形できないとはどういうことか、視覚的に見てみましょう。まず次のように、布の上に置かれた時計をいくつかの角度から撮影します。(わかりやすくするために写真をまとめて gif 動画にしました)。
この写真1枚1枚を、床に敷いてある布をベースにこの記事の実装を使って変換し、同じ方向から見たような形にしてみます。(注: この操作を image alignment と呼ぶようですが、日本語訳がわかりません。どなたかご存知でしょうか?)。今回は正面から見た写真になるように変換しました。
少しノイズがあって画面は揺れますが、 image alignment を行ったことでホモグラフィーの対象となった平面(床の布)は、同じ方向から撮影されたような形になっています。一方で、ホモグラフィーで対象とされていない時計の部分は大きく歪みました。
ただ、この歪み方、興味深いことに規則性があります。時計は床に近い部分では少ししか歪まず、離れていくに従って歪みが大きくなっていく様子が伺えます。この規則性が P+P のポイントになっていて、 ある平面を設定してホモグラフィーを行った際、平面から離れている距離と、その歪み方には何らかの相関関係がある 、ということが言えそうな気がします。
そして実際に P+P はその相関関係から、空間上の点の平面からの距離を求めることができます。なんだか深度推定の話に近づいて来ました。
図を使って考える
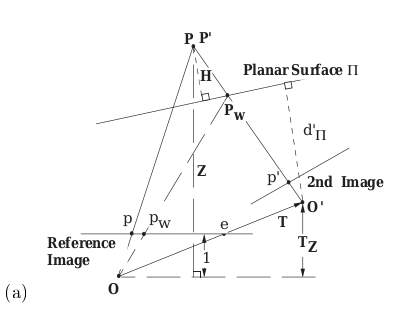
イメージはなんとなく分かったので、次は数式で見てみます。以下の内容は Michal Irani 氏の論文 "Parallax Geometry of Pairs of Points for 3D Scene Analysi" の図と Appendix の内容に基づきます。
図は "Parallax Geometry of Pairs of Points for 3D Scene Analysis" より引用
今、2nd Imageと書かれている位置から撮影された画像を、 Planar Surface $\Pi$ を軸にホモグラフィーで変換し、 Reference Image の位置から撮影されたような形に変形させることを考えます。
ホモグラフィーによって 2nd Image を Reference Image の位置から撮影したように変形させた場合、 Planar Surface $\Pi$ については正しく変換ができます。一方で先程の例にあったように、Planar Surface $\Pi$ から外れた点については、変換によって歪んだ位置に移動することになります。これはこの図ではどれに対応しているのでしょうか。
これは、$p_w$ になります($w$ は warp の頭文字)。
2nd Image をReference Image から撮影した画像に変換するのであれば、2nd Image上の点 $p'$ はReference Image上の点 $p$ に移動するのが理想的な動きです。しかしながらホモグラフィーは Planar Surface $\Pi$ 上の点しか正しく変換できません。その結果、2nd Image上の点 $p'$ は あたかも Planar Surface $\Pi$ 上の点 $P_W$ に対応した点であると数式上で処理され、 Reference Image には $p_w$ の位置に移動します 。本来あるべき位置 $p$ ではなく、点 $p_w$ に移動してしまうこれこそが歪みの原因です。
この歪みの関係については、この図に登場する変数で記述ができます。導出過程は細かくて分量もあるので割愛しますが、結論としては、$T_z \neq 0$ のとき
p = p_w + \frac{H}{Z} \frac{T_z}{d'_\pi} (p_w - e)
$T_z = 0$ のとき
p = p_w - \frac{H}{Z d'_\pi}t
となります。ただしそれぞれの文字の意味は以下のとおりです。
- $p$: 空間上の点 $P$(点 $P'$)が Reference Image 上に写る位置
- $p_w$: ホモグラフィーによって2nd Imageの点 $p'$ が移動してきた位置
- $H$: Planar Surface $\Pi$ から空間上の点 $P$ までの距離
- $Z$: 位置 $O$ から空間上の点 $P$ までのベクトルのZ成分
- $T$: 位置 $O$ から位置 $O'$ までの移動を表すベクトル
- $T_z$: $T$のz座標成分。z座標は Reference Image に対して垂直な方向
- $d'_\pi$: 位置 $O'$ から Planar Surface $\Pi$ までの距離
- $e$: 位置 $O$ からエピポールへのベクトル
Planar Surface Πを無限遠に設定する
(ここからは Mannequin Challenge の Supplementary Material の内容となります)
P+P を使うことで、特定の平面からの距離 $H$ やカメラから平面までの距離 $Z$ などが数式で表されることがわかりました。ただ、 Mannequin Challenge Dataset の作成をするに当たって知りたい情報は、空間上の点の深度(位置 $O$ から見た深度)であり、 $Z$ だけです。それ以外のパラメータはあまり興味がありません。
P+P の元の式だと文字が多くて単純に $Z$ が求まりません。そこで、今特に考える必要の無い $d'$ や $H$ などを無視するために、 Planar Surface $\Pi$ を無限遠に設定します。
Planar Surface $\Pi$ が無限遠に設定されると $\frac{H}{d'_\pi}$ はキャンセルされて1となり、さらにロピタルの定理を使うことで式を変形していくことができます。結果だけを書くと以下のようになります。
D_{PP}(p) = \frac{||t_3 p_w - K t||}{||p-p_w||}
p_w = \frac{A' p'}{{a'}_3^T p'}
A' = KRK^{-1}
P+P の原著と Mannequin Challenge の Supplimental Material の間で文字の定義や使う文字が変わってしまっているので非常に混乱してしまうのですが、この式における各文字の意味は以下の通り。
- $D_{PP}(p)$: 位置 $O$ から空間上の点 $P$ までのベクトルのZ成分。P+Pの原著でいう $Z$ のこと。
- $t$: 位置 $O'$ から位置 $O$ までの移動を表すベクトル。P+Pの原著と逆の定義。
- $K$: カメラの内部パラメータ
- $A'$: ホモグラフィー
- $a'$: $A'$ の3行目
- $R$: 位置 $O'$ での向きから位置 $O$ での向きの変換を表す行列。P+Pの原著と逆の定義。
ひとまず、Planar Surface Πを無限遠に設定することで文字が減り、 $D_{PP}(p)$ を求めるために必要なパラメータは $K$, $R$, $t$, $p$, $p'$ の5つに減りました。
$K$, $R$, $t$ は SfM を行った時点で分かっています。そのためあとは $p$, $p'$ だけです。
準備2: 深層学習を用いて p と p' のペアを求める
全ピクセル p について p' を求めることは意外と難しい
$p$ と $p'$ は、空間上のある点Pが二枚の画像のどこに写り込んでいるかをそれぞれ表した値です。二枚の画像を比較して、共通の点Pを見つけ、それが写っている座標を求めれば良いことになります。「あぁそれはSIFT特徴量とかを使えばすぐにわかる」と言いたいところです。
※図はイメージです
しかし問題があります。今は $D_{PP}(p)$ を全ピクセルについて求めたいため、全ピクセル $p$ について、 $p$ と $p'$ のペアを求める必要があります。しかしながら SIFT 特徴量などは全ピクセルに対して定義することができません。それはすべてのピクセルに一意な特徴が見いだせないからです。先程の画像で言えば、時計の表面のツルツルしている部分は全部同じような黒色をしていて、隣接するピクセル同士で明確に異なる特徴を見出すことができません。
この問題、一般的には Stereo Matching と呼ばれる問題になります。 Mannequin Challenge の論文は P+P を行うためにどの手法を採用したのかというと、深層学習をベースとしたオプティカルフロー算出手法である FlowNet2.0 を利用しています。
FlowNet2.0 による p と p' の算出
ここまでで記事の分量が増えてきてしまったので、FlowNet2.0の詳細は割愛します。今回は NVIDIA社による実装を使ったので、使い方等はこの公式リポジトリを確認してください。
ここでの内容を簡単に説明すると、 FlowNet2.0 では2枚の画像を入力し、その画像間での各ピクセルの動きを .flo ファイルに出力します(ちなみにこの処理、私の普段使いの GTX1060 では GPU メモリが不足しました。ハイエンドGPUが必要になるみたいです)。出力結果は次のようになります。
色がついていますが、これはベクトルの方向(上下左右)とベクトルの長さを色で表現したものになります。 "optical flow color chart" で検索すると凡例が出てきます。
FlowNet2.0 によって、任意のピクセル $p$ について、その位置と二枚目の画像上の $p'$ との間のベクトルが求まりました。この FlowNet2.0 の出力結果を $F(p)$ で表すと、 $p'$ は
p' = p + F(p)
で求まります。
準備3: P+P の実装
1. 画像ペアの作成
さて、これで P+P を使ってデプスマップを作成する方法がすべてわかりました。早速実装します。
まずはじめに、 P+P でデプスマップを作成するための画像のペアを決めます。これについては、論文中に以下のアルゴリズムに基づき決定すると記載があります。
- Reference Image ($I^r$) を決める。(今回は映像の全フレームを $I^r$ としてそれぞれ計算しました。)
- I^r に対して、 Second Image となる $I^s$ を以下の式に基づいて決める。ただし $d^{rj}$ は $I^r$ と $I^j$ の距離、 $o^{rj}$ は共通に含まれる SfM の特徴点の割合である。また $I^r$ と $I^s$ は10フレーム以上離れないとする。
s = \arg \max_j d^{rj} o^{rj}
o^{rj} = \frac{2 |V^r \cap V^j|}{|V^r| + |V^j|}
o^{rj} < 0.6
これを以下のようなコードで実装しました。ただし6行目でインポートしている read_write_model は COLMAP のプロジェクトで用意されている Python スクリプトになります。
import os
import sys
import numpy as np
import glob
import shutil
import read_write_model
if __name__ == "__main__":
if len(sys.argv) != 3:
print("Usage: python read_write_model.py path/to/model/folder [.txt,.bin]")
return
cameras, images, points3D = read_write_model.read_model(
path=sys.argv[1], ext=sys.argv[2])
dir_path = '/home/ohashi/Documents/mannequin_challenge_v6'
for i in range(len(glob.glob('%s/images/*.png' % dir_path))):
# for i in range(1):
im_num = i+1
# 元画像の特徴点の数
total_feature = len(images[im_num].point3D_ids)
# 元画像の特徴点
idx = images[im_num].point3D_ids[images[im_num].point3D_ids != -1]
distance = np.zeros((20, 1))
count = np.zeros((20, 1))
d_o_value = np.zeros((20, 1))
total_feature2 = np.zeros((20, 1))
cand = range(-min(10, im_num-1)-1,
min(len(glob.glob('%s/images/*.png' % dir_path))-im_num, 10))
cand.remove(-1)
for j in range(len(cand)):
# カメラ間の絶対距離
distance[j] = np.linalg.norm(
images[im_num].tvec-images[im_num+cand[j]+1].tvec)
total_feature2[j] = len(images[im_num+cand[j]+1].point3D_ids)
# 候補画像の特徴点
b = images[im_num+cand[j] +
1].point3D_ids[images[im_num+cand[j]+1].point3D_ids != -1]
for k in range(len(idx)):
if np.any(b == idx[k]):
count[j] = count[j]+1
# for j in np.where(count/total_feature>0.6)[0]:
for j in np.where(2*count/(total_feature+total_feature2) > 0.6)[0]:
# d_o_value[j] = distance[j]*count[j]/total_feature
d_o_value[j] = distance[j]*2*count[j] / \
(total_feature+total_feature2[j])
s = cand[np.argmax(d_o_value)]
if np.max(d_o_value) != 0:
if not os.path.exists('%s/pair_image/%d' % (dir_path, i)):
os.mkdir('%s/pair_image/%d' % (dir_path, i))
shutil.copy2('%s/images/image_%d.png' % (dir_path, i+224),
'%s/pair_image/%d/r_image_%d.png' % (dir_path, i, i+224))
shutil.copy2('%s/images/image_%d.png' % (dir_path, i+224+s+1),
'%s/pair_image/%d/s_image_%d.png' % (dir_path, i, i+224+s+1))
print("num_cameras:", len(cameras))
print("num_images:", len(images))
print("num_points3D:", len(points3D))
これで画像のペアが求まります。
2. FlowNet2.0 の実行
これは先程説明したとおり、 NVIDIA社による実装 を使用します。
3. デプスマップの作成
あとは $D_{PP}(p)$ の計算だけです。
$D_{PP}(p)$ の式は各ピクセルごとの計算となっていますが、各ピクセルごとの計算を for 文で回していたら時間がかかってしまうので、 numpy のブロードキャストルールをうまく活用して、1回の計算で全ピクセルの $D_{PP}(p)$ を求めます。
plane_plus_parallax.py
import read_write_model
import numpy as np
def camera_intrinsic_mat(cameras_param, camera_id):
f_x = cameras_param[camera_id].params[0]
f_y = cameras_param[camera_id].params[1]
c_x = cameras_param[camera_id].params[2]
c_y = cameras_param[camera_id].params[3]
return np.array([[f_x, 0, c_x], [0, f_y, c_y], [0, 0, 1]])
def camera_rotation_mat(images_param, ref_img_id, src_img_id):
ref_img_qvec = images_param[ref_img_id].qvec
src_img_qvec = images_param[src_img_id].qvec
ref_img_rotmat = read_write_model.qvec2rotmat(ref_img_qvec)
src_img_rotmat = read_write_model.qvec2rotmat(src_img_qvec)
return ref_img_rotmat @ np.linalg.inv(src_img_rotmat)
def camera_transpose_vec(images_param, ref_img_id, src_img_id):
ref_img_tvec = images_param[ref_img_id].tvec
src_img_tvec = images_param[src_img_id].tvec
return ref_img_tvec - src_img_tvec
def homography(K, R):
return K @ R @ np.linalg.inv(K)
def p_dash(p_mat, F):
return p_mat + F
def p_warp(p_d_mat, A_d):
numer = A_d @ p_d_mat.reshape(1024, 1856, 3, 1)
denom = A_d[2] @ p_d_mat.reshape(1024, 1856, 3, 1)
return numer.reshape(1024, 1856, 3) / denom
def D_pp(p_mat, F, K, R, t):
A_d = homography(K, R)
p_d_mat = p_dash(p_mat, F)
p_w_mat = p_warp(p_d_mat, A_d)
numer_mat = t[2] * p_w_mat - K @ t
denom_mat = p_mat - p_w_mat
numer = np.linalg.norm(numer_mat, ord=2, axis=2)
denom = np.linalg.norm(denom_mat, ord=2, axis=2)
return numer / denom
util.py
from PIL import Image
import numpy as np
from pylab import cm
def normalize_array(x, axis=None):
minval = x.min(axis=axis, keepdims=True)
maxval = x.max(axis=axis, keepdims=True)
result = (x-minval)/(maxval-minval)
return result
def export_mat(mat, filepath):
img = Image.fromarray(np.uint8(cm.jet(mat)*255))
if img.mode != "RGB":
img = img.convert("RGB")
img.save(filepath)
main.py
import read_write_model
import read_dense
import util
import plane_plus_parallax as ppp
import numpy as np
import os
import re
import mmcv
import pylab as plt
from pylab import cm
if __name__ == "__main__":
PROJECT_DIR = "/mnt/mannequin-challenge-EscolaComercioDoPorto/"
FN2_WORKSPACE = PROJECT_DIR + "FlowNet2/"
FN2_OUTPUT_DIR = FN2_WORKSPACE + "output/"
IMAGE_PAIR_DIR = FN2_WORKSPACE + "pair_image/"
CAMERA_PARAM_DIR = PROJECT_DIR + "radial_model_SfM/dense/sparse/"
D_PP_OUTPUT_DIR = PROJECT_DIR + "D_pp/"
BEFORE_DENOISING_OUTPUT_DIR = PROJECT_DIR + "Before_Denoising/"
DENOISING_OUTPUT_DIR = PROJECT_DIR + "Denoising/"
MVS_DEPTH_DIR = PROJECT_DIR + "radial_model_SfM/dense/stereo/depth_maps/"
# import parameters
cameras_param = read_write_model.read_cameras_binary(
os.path.join(CAMERA_PARAM_DIR, "cameras.bin"))
images_param = read_write_model.read_images_binary(
os.path.join(CAMERA_PARAM_DIR, "images.bin"))
images_id_dict = {}
for key in images_param:
images_id_dict[images_param[key].name] = images_param[key].id
# calculate D_pp for each pair of images
pair_number_list = sorted(os.listdir(FN2_OUTPUT_DIR))
for pair_number in pair_number_list:
path_to_flowfile = FN2_OUTPUT_DIR + \
str(pair_number) + "/inference/run.epoch-0-flow-field/000000.flo"
path_to_image_dir = IMAGE_PAIR_DIR + str(pair_number) + "/"
os.chdir(path_to_image_dir)
files = os.listdir()
print("pair number: ", pair_number)
print("images: ", files)
# find image id (ref_img_id, src_img_id)
ref_img_name = [item for item in files if item.startswith("r_")][0]
ref_img_name = ref_img_name.replace("r_", "")
src_img_name = [item for item in files if item.startswith("s_")][0]
src_img_name = src_img_name.replace("s_", "")
ref_img_id = images_id_dict[ref_img_name]
src_img_id = images_id_dict[src_img_name]
# intrinsic, extrinsic, homography
# edit cx and cy of camera intrinsics
# because size of the image is not (1899, 1062) but (1856, 1024)
camera_id = 1
cameras_param[camera_id].params[2] = 1856/2
cameras_param[camera_id].params[3] = 1024/2
K = ppp.camera_intrinsic_mat(cameras_param, camera_id)
R = ppp.camera_rotation_mat(images_param, ref_img_id, src_img_id)
t = ppp.camera_transpose_vec(images_param, ref_img_id, src_img_id)
A_d = ppp.homography(K, R)
# initialize p matrix
# p_mat.shape == (1062, 1899, 3) with z=1 for all elements
p_x_mat = np.array([[x, 0, 0] for x in range(1856)])
p_y_mat = np.array([[[0, y, 0]] for y in range(1024)])
p_z_mat = np.array([0, 0, 1])
p_mat = p_x_mat + p_y_mat + p_z_mat
# import optical flow data
# flow_field.shape == (1024, 1856, 2), which doesn't contain z param
# F.shape == (1024, 1856, 3) with z=0 for all elements
flow_field = mmcv.flowread(path_to_flowfile)
F = np.pad(flow_field, [(0, 0), (0, 0), (0, 1)], "constant")
# compute D_pp for all pixels at once
D_pp_mat = ppp.D_pp(p_mat, F, K, R, t)
# export mvs_depth_mat
min_depth, max_depth = np.percentile(mvs_depth_mat, [5, 95])
mvs_depth_mat[mvs_depth_mat < min_depth] = min_depth
mvs_depth_mat[mvs_depth_mat > max_depth] = max_depth
mvs_depth_mat_normalized = util.normalize_array(mvs_depth_mat)
util.export_mat(mvs_depth_mat_normalized,
os.path.join(BEFORE_DENOISING_OUTPUT_DIR, str(pair_number)+".png"))
# export D_pp
min_depth, max_depth = np.percentile(D_pp_mat, [5, 95])
D_pp_mat[D_pp_mat < min_depth] = min_depth
D_pp_mat[D_pp_mat > max_depth] = max_depth
D_pp_mat_normalized = util.normalize_array(D_pp_mat)
util.export_mat(D_pp_mat_normalized,
os.path.join(D_PP_OUTPUT_DIR, str(pair_number)+".png"))
あとはこれを動かしましょう。
余談: 2つのデプスマップを比較
計算がうまく行けばデプスマップが生成されます。昨日作成した MVS によるデプスマップと比較してみましょう。
MVS (COLMAP) によるデプスマップ
FlowNet2.0 と P+P によるデプスマップ
P+P の結果は...うーん...。ノイズ除去のために使うデータがこれで良いのか?と。(実はこの gif の部分はまだいい方で、P+Pによるデプスマップがノイズだらけでよくわからないところも実際はありました。)
P+P のプログラムにバグがあるんじゃないかと思ったものの、ざっと見ても見つかりませんでした。むしろ FlowNet2.0 の出力データを確認すると、それ自体にノイズが結構載っていました。そのためこのノイズの原因は FlowNet2.0 によるオプティカルフロー推定のノイズが元になっているのではないかと思います。 P+P は理論的に考えるとこのようなノイズが乗ることはありません。
本題: ノイズ除去
P+P について色々見てきましたが、最後に本題のノイズ除去を行います。ノイズ除去自体は簡単で、まず以下の数式で $\Delta(p)$ を求めます。
\Delta(p) = \frac{| D_{MVS}(p) - D_{pp}(p) |}{D_{MVS}(p) + D_{pp}(p)}
そして、 $\Delta(p) > 0.2$ となるピクセルは「2つの手法で大きく異なるデプス値が求まったため信頼できない」と判断し、除去します。実際にコードにしてみると次の通り。さきほどの main.py の続きになります。
main.py つづき
# denoising
mvs_depth_mat = read_dense.read_array(
MVS_DEPTH_DIR + ref_img_name + ".geometric.bin")
mvs_depth_mat = mvs_depth_mat[19:1043, 21:1877]
delta_p_mat = np.abs(mvs_depth_mat - D_pp_mat) / \
(mvs_depth_mat + D_pp_mat)
mvs_depth_mat_denoised = np.copy(mvs_depth_mat)
mvs_depth_mat_denoised[delta_p_mat > 0.2] = 0
# export mvs_depth_mat_denoised
min_depth, max_depth = np.percentile(mvs_depth_mat_denoised, [5, 95])
mvs_depth_mat_denoised[mvs_depth_mat_denoised < min_depth] = min_depth
mvs_depth_mat_denoised[mvs_depth_mat_denoised > max_depth] = max_depth
mvs_depth_mat_normalized = util.normalize_array(mvs_depth_mat_denoised)
util.export_mat(mvs_depth_mat_normalized,
os.path.join(DENOISING_OUTPUT_DIR, str(pair_number)+".png"))
これを実行すると次のようになります。
うーん...。頑張った割にあまり嬉しさがないこの感じ...。
この gif ではノイズ除去の影響で、最後のあたりのフレームでデータが大きく欠損しています。 Mannequin Challenge Dataset はこういったデータが大きく欠損したフレームを除外し、データが十分多く含まれているフレームのみをデータセットに含めるという操作を行います。
まとめ
ノイズ除去の結果は、頑張った割になんだかなぁという感じでした。とはいえこれが論文に書かれていた内容なので、なぜこれが論文中で採用されたのか考えてみました。
考察1: データが減ることよりもデータのノイズを嫌った?
今回の記事ではあまり書いていませんが、 Mannequin Challenge Dataset を作るためにいろいろな動画を使ってみました。がしかし、モーションブラーが大きかったり画面が暗かったりして、元データを作るところ(昨日書いた内容)自体苦戦しました。 COLMAP の計算がうまく行ったかのように見せかけて、結果を確認してみるとノイズだらけでよくわからない箇所がある、ということも多々ありました。
FlowNet2.0 と P+P を用いた今日の内容によるノイズ除去は、そういう MVS で生成された「FlowNet2.0 よりも酷いノイズを除去するため」という目的で採用されたのかなと思います。 Mannequin Challenge Dataset の論文の著者は、 YouTube に Mannequin Challenge の動画はたくさんあるんだから、データをたくさん作ることよりもむしろ使えないなデータをいかに効率的に除外していくかに集中していたのではないでしょうか。
考察2: FlowNet2.0 を使ったのは効率化のため?
Stereo Matching を行うために FlowNet2.0 が使われたと説明しましたが、 FlowNet2.0 は Stereo Matching というよりかは Optical Flow のためのツールかと思います。 Stereo Matching のためのツールは、最近では機械学習版もそれなりに提案されているので、そこであえて FlowNet2.0 を採用したのはなぜなのか。
この点についてはそこまで深く分析できなかったのですが、 FlowNet2.0 は計算結果を出すまでの時間が1秒程度であり、それなりに速いです。この速さが FlowNet2.0 を採用した理由なのかなぁ...と考えています(もっと別の目的があるかもしれません)。
本記事の最後に書くのは少し変かもしれませんが、昨日の記事で説明した MVS も、内部的には Stereo Matching を行っています。ピクセルごとにデプスを求めるためには(単眼深度推定をしない限り) Stereo Matching が避けられません。昨日使ったツールである COLMAP は、 Patch Match と呼ばれる手法で Stereo Matching を行っています。が、 これはめちゃくちゃ時間がかかります 。今回の動画を MVS でデプスマップ作成したときは、私の GTX1060 を使ってもだいたい1日ちょっとかかりました。
それと比較すれば、 FlowNet2.0 はノイズは多いけれど速度が速いので、便利だと捉えられるかもしれません。(ただし、そもそも FlowNet2.0 以外でも速度が速い手法はあるんじゃないかとも考えられますし、そこはまだ謎です)。
おわりに
長かった「できる!Mannequin Challenge Dataset」でしたが、なんとか終わりました。今回は Mannequin Challenge Dataset の論文を追っていく感じだったので、言われたとおりに従えばなんとかできるという内容でした。ただ、この論文を書いた人はこれをアイディアとして思いつき、ノイズ周りの困難を乗り越えて論文化したのだと考えると、やっぱりすごいです。
また今回やってみて、改善の余地があると思ったのは主に Stereo Matching まわり(FlowNet2.0など)です。ここは長年研究されているとはいえまだまだ綺麗なデータを生成できていないので、これからの研究成果に注目です。
参考文献
Irani, M. and Anandan, P., 1996, April. Parallax geometry of pairs of points for 3d scene analysis. In European Conference on Computer Vision (pp. 17-30). Springer, Berlin, Heidelberg.
Li, Z., Dekel, T., Cole, F., Tucker, R., Snavely, N., Liu, C. and Freeman, W.T., 2019. Learning the Depths of Moving People by Watching Frozen People. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 4521-4530).
Michal Irani - Plane + Parallax https://www.youtube.com/watch?v=CetSbajps88&t=357s
Image Alignment (Feature Based) using OpenCV (C++/Python) https://www.learnopencv.com/image-alignment-feature-based-using-opencv-c-python/