【MATLAB】角度の平均を求める

意外とmatlabで角度の平均を求める記事が無かったので実装してみた．

実装

y = calcThetaMean([0 90]);   % y = 45
y = calcThetaMean([0 -180]); % y = -90
y = calcThetaMean([90 270]); % y = 180

function output = calcThetaMean(theta)
thetaRad = deg2rad(theta);      % deg -> radianに変換
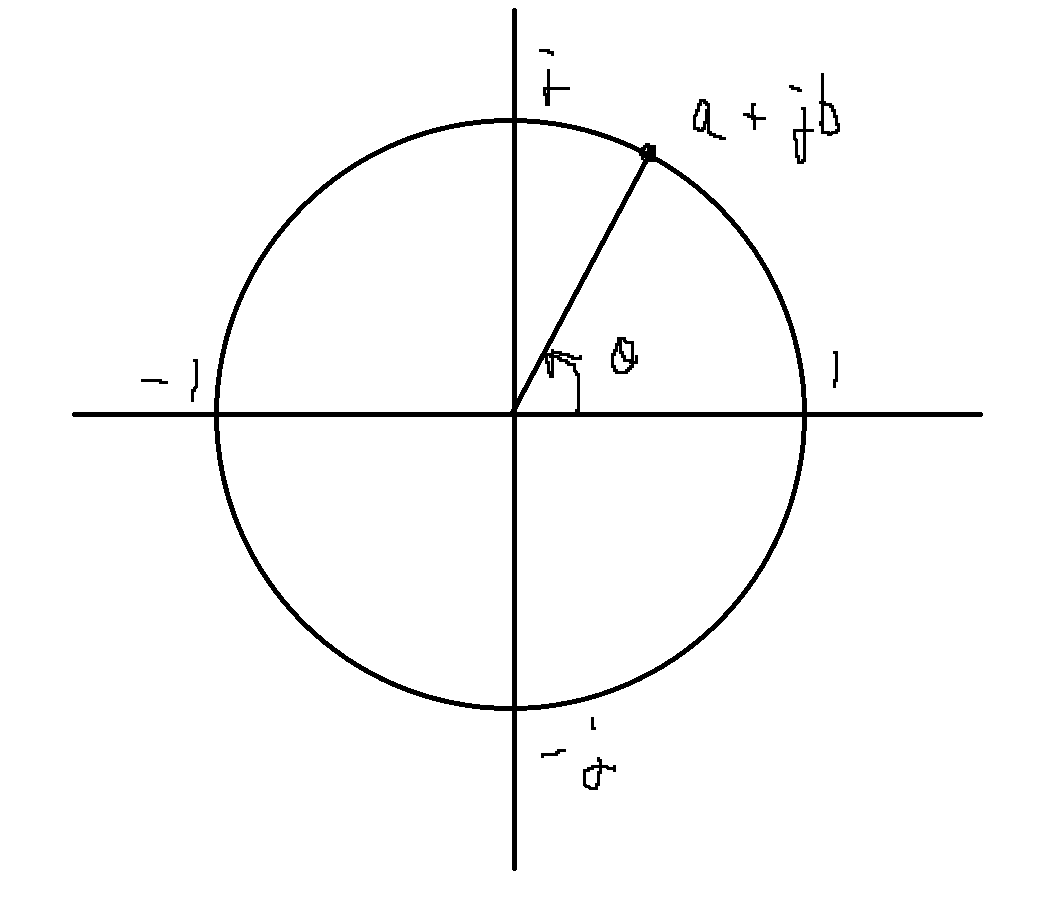
Vn = exp(1i*thetaRad);          % 複素数にする
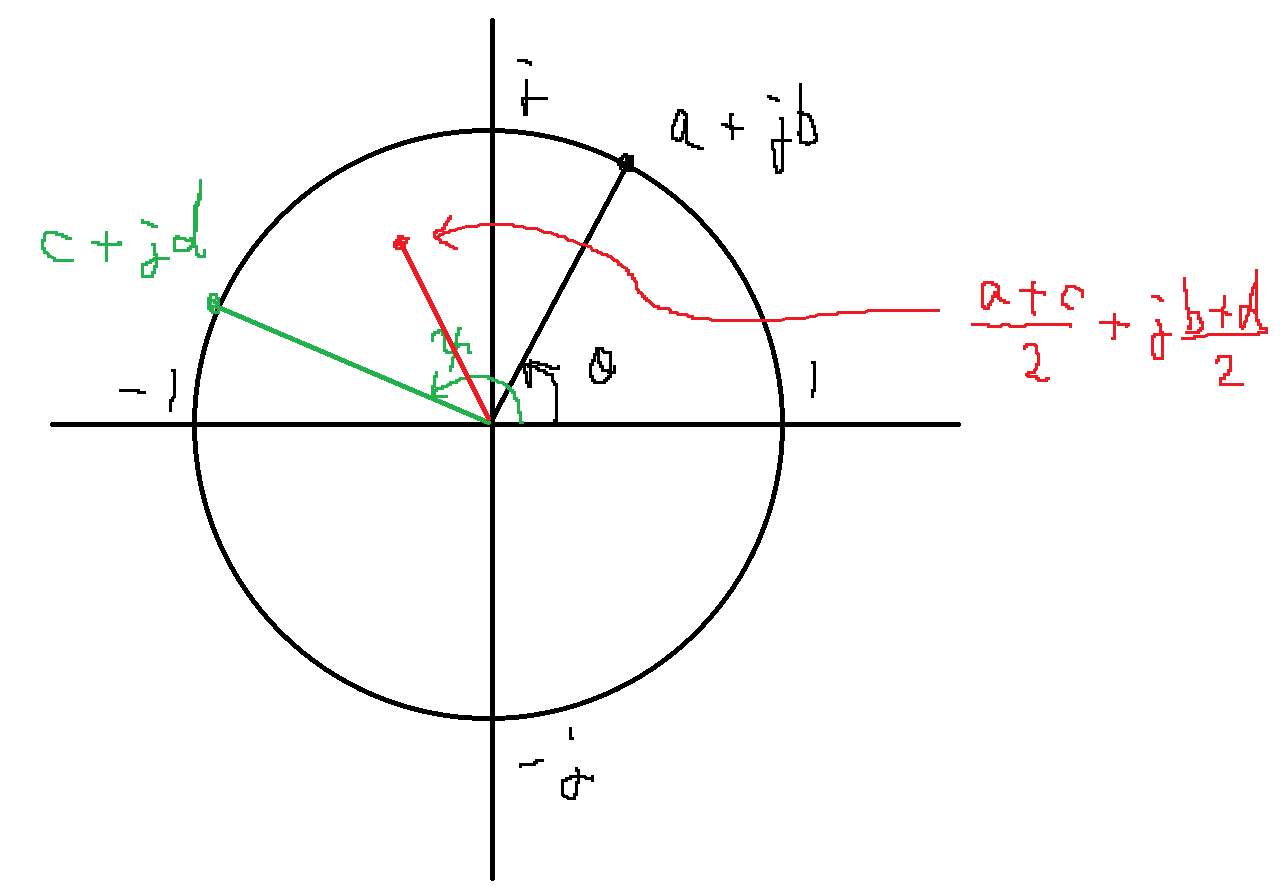
VnAvg = mean(Vn);               % 点の平均を求める
thetaMeanRad = angle(VnAvg);    % 位相角[-π,π]を求める
output = rad2deg(thetaMeanRad); % radian -> degに変換
end

解説

Vn = exp(1i*thetaRad);          % 複素数にする

これをするとラジアンが複素平面上の点になる．これならthetaが45度でも405度でも-315度でも全部同じ値になるはずである．これにより角度計算の面倒な部分を考えなくて良くなる．

VnAvg = mean(Vn);               % 点の平均を求める

各点の平均（中心点）を求める．

thetaMeanRad = angle(VnAvg);    % 位相角[-π,π]を求める

あとは複素平面の点をラジアンに戻せばおけまる水産である．

rad2deg(angle(mean(exp(1i*deg2rad([0 90])))))

で1行に書くこともできる．

y = calcThetaMean([0 90 180]); y = 90

として3角度とかの平均も求められる．

疑問（解決せず）

基本的にこれで良いと思うんだけど，平均が0度付近とか180度付近で微妙になる感じはある．

y = calcThetaMean([10 350])  % y = -1.6148e-15, きっちり0にならない
y = calcThetaMean([10 -10])  % y = 0, 上と同じになるはずだがきっちり0になる

y = calcThetaMean([160 200]) % y = 180, これは良いが
y = calcThetaMean([170 190]) % y = -180, なぜかマイナスになる
y = calcThetaMean([170 -170]) % y = 180, 上と同じになるはずだが180度になる 

↑こんな感じ．
最初の方に「thetaが45度でも405度でも-315度でも全部同じ値になるはずである」と言ったが，実は同じ値にならないっぽい．

x1 = exp(1i*deg2rad(350)); % x1 = 0.9848 - 0.1736i
x2 = exp(1i*deg2rad(-10)); % x2 = 0.9848 - 0.1736i
norm(x1-x2) % 5.5511e-17

として，複素数にした時若干の誤差があるっぽい．なんか腑に落ちないが気にしてたら狂うのでMathWorksの実装が悪いんだよということで、この辺で切り上げておく．

y = calcVeryBadThetaMean([10 350])  % y = 0になって嬉しいね

function output = calcVeryBadThetaMean(theta)
thetaRad = deg2rad(theta);
Vn = exp(1i*thetaRad);
VnAvg = mean(Vn);
thetaMeanRad = angle(VnAvg);
output = rad2deg(thetaMeanRad);
output = round(output*(1e+6))/(1e+6); % 誤差るなら　丸めてしまおう　ホトトギス
end

あとは[10 350]で誤差があったが[10 -10]だと上手くいったので，入力する角度を[-pi pi]で正規化しておくといいかも．知らんけど．

本記事は雑に書いたので以下のようなちゃんとした記事を見に行くと勉強になると思われる．