この記事について
AWS Braket が公開されてから、一般の人にとっても量子コンピュータの実機に触れる機会が増え、それに伴い、私も量子コンピュータのお勉強をしています。
Braketではゲート型の最適化を行うにあたってQAOAというアルゴリズムを使用します。
AWS Braketのサンプル上ではGraph Coloring Problem という問題を解いており、「各ノードに赤や青の色をつけ、色の異なるノード間の各枝に点数をつけていきより良い点をしよう」という問題の求解を行っています。
こちらの問題ですが、以下の式で表されるコスト関数を定義し、($z_n= {-1,1}$, $J$は枝間の重み)それを最小化する問題に帰着できます。
H_{C}=\sum_{i>j} J_{i,j} z_{i} z_{j},
このような問題に帰着できるものであれば、AWS Braketのサンプルを流用することで動かすことができますが、最適化問題をより一般的に表すには、以下の通り線形項も加味する必要があります。
H_{C}=\sum_{i>j} J_{i,j} z_{i} z_{j} + \sum_{i=1}^{n} h_{i} z_{i}
AWSのサンプルをそのまま動かすだけでは上記の問題を正確に解くことができません。(近似アルゴリズムなので別のアプローチでももちろん正確ではないが、そのまま使うよりは正確です。)
なのでこういった最適化問題を解くことができるような実装をAWS Braket上で行いました。
とはいえ、それを紹介する前にAWS Braket上でQAOAがどのように表現されているかを示す必要があるかと思い、本記事ではまずAWS Braket上でQAOAがどのように実装されているかを解説していこうと思います。
上記背景から本記事は**あくまでAWS BraketのQAOAサンプルコードを解説する**という記事となっています。
ソースコード等一切変更せず解説を行っているのでご注意ください。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
解説の対象
今回はAWS Braketのサンプルを直接解説していこうと思いますので こちらのソースコードを解説していきます。
こちのソースコードはBraketを起動した際に notebookインスタンス内に自動で連携され、だれでも最初から使えるようになるので
実際に動かして使ってみたい人は Braketの利用開始をしてみて実際に使ってみてください。
起動直後に連携されるソースコード内の
/Braket examples/ hybrid_quantum_algorithms/QAOA
のなかに入っているはずなのでそちらを見て触ってみてもいいかと思います。(2021/01/18現在)
ソースコードの概要
BraketのQAOAサンプルコード内を見てみると以下の3つのソースコードが入っているかと思います。
- QAOA_braket.ipynb
- utils_classical.py
- utils_qaoa.py
QAOA_braket.ipynb では、QAOAの簡単な概要、問題の定義、QAOAのパラメータ定義、QAOAの呼び出し、古典最適かとの比較などの呼び出し側で記述したり、比較したりするようなソースコードが書かれています。
util_classical.py は比較用に使う古典最適化の実体が記述されています。そのため、今回はこちらの説明は本質的ではないため、割愛させていただきます。
utils_qaoa.py はQAOAの実体が記述されており、実際の回路等の記載が行われています。
ということなので今回は
- QAOA_braket.ipynb
- utils_qaoa.py
特に、utils_qaoa.pyの解説をしていこうと思います。
詳細
QAOA_braket.ipynb
まずはQAOAを呼び出す元のソースコードから解説していきます。
こちらnotebook用のソースコードであるのでQAOAの簡単な説明も記載してあります。
というわけでせっかくなのでその辺も追っていきながら説明をしていきます。
QAOA の概要
QAOAの概要が記載されています。
QAOAはあくまで近似最適化アルゴリズムであることやNISQアルゴリズムとして有力な手段として認識されていて、古典計算と量子計算を組み合わせて行うハイブリッド量子アルゴリズムに分類されます。
Braket では、オープンソースのscipyを使うことで古典最適化部分を行っています。
※注意点ですが、本記事で説明を割愛させていただくutils_classical.pyはQAOAのハイブリッドの古典計算とは全く関係ありません。
QAOAの古典計算はutils_qaoa.pyに記載してあり、utils_qaoa.pyは今回の説明の対象なので安心してください。
さらに興味深い話がありこちらのソースコード上でQAOAがDeep Learningと似ているよねという話が以下の図を用いて示されていました。
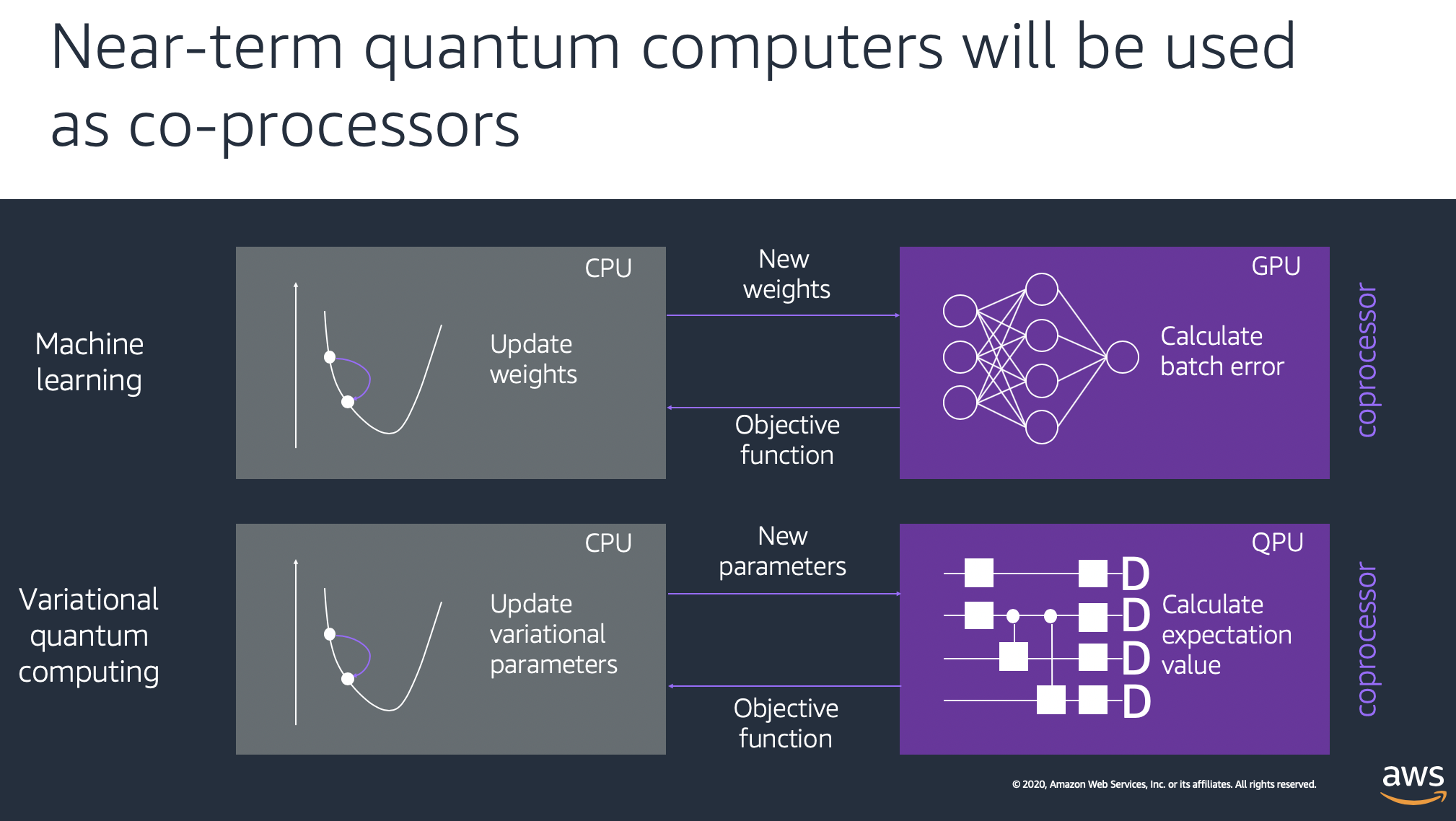
引用: https://github.com/aws/amazon-braket-examples/blob/main/hybrid_quantum_algorithms/QAOA/QAOA_braket.ipynb
本稿の趣旨ではないので説明は割愛します。
興味のある方はソースコードを読んでみてください。
バイナリ二次計画問題
今回はGraph Coloring 問題という問題を使用していきます。
なのでこちらでさっさとGraph Coloring 問題の定式化を説明していきましょう。
とは言ってもかなり簡単なので構えずに読み流す程度で大丈夫だと思います。
Graph Coloring Problem は「各ノードに赤や青の色をつけ、色の異なるノード間の各枝に点数をつけていきより良い点をしよう」という問題の求解を行っています。
つまり、なるべく隣り合うものは別の色で塗ろう!という配色問題ですね。
今回は簡単にサンプルを実装しているようなので2色で色分けをしている問題となりmさう。
こちらの問題ですが、以下の式で表されるコスト関数を定義し、($z_n= {-1,1}$, $J$は枝間の重み)それを最小化する問題に帰着できます。
H_{C}=\sum_{i>j} J_{i,j} z_{i} z_{j},
QAOAの流れ
QAOAの流れは
こちらの記事 をぜひ見ていただきたいのですが、本記事でも簡単に触れます。
以下QAOAの手順となります。
- 重ね合わせ状態$|s\rangle = |+\rangle^{\otimes n}$を作る。
- パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$をかけていき、状態$|\beta, \gamma \rangle$を得る。
- 量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する
- $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。
- 最適解 $\beta^{ * }$,$\gamma^{ * }$を得るまで1~4を繰り返す。
- $|\beta^{ * } , \gamma^{ * } \rangle$ をZ基底で測定し、良さそうな測定結果を解として出力する。
特に2ではAWS Braketのソースコード上でも触れられている以下の式を適用するのと同値です。
|\beta, \gamma \rangle = U_{x}(\beta_{p})U_{zz}(\gamma_{p}) \cdots U_{x}(\beta_{1})U_{zz}(\gamma_{1}) |s\rangle
また、
{e^{-i\gamma_{i} (Z_iZ_j)}= CX_{i, j} R_{Z_j}(2\gamma_{i}) CX_{i, j}} \\
{e^{-i\gamma_{i} (X)}= R_{X}(2\beta)}
であることを念頭に置けば回路に落とし込むことができそうです。
ソースコードの流れ
ではソースコードの流れを追っていきます。
まずインポート分野AWS S3 Bucketの設定などがありますが、このあたりの説明は省略します。
問題の定義
まずはグラフの定義をしていきます。
AWS Braket上は以下の通りのグラフ定義になっています。
# setup Erdos Renyi graph
n = 10 # number of nodes/vertices
m = 20 # number of edges
# define graph object
G = nx.gnm_random_graph(n, m, seed=seed)
# positions for all nodes
pos = nx.spring_layout(G)
# choose random weigths
for (u, v) in G.edges():
G.edges[u,v]['weight'] = random.uniform(0, 1)
# draw graph
nx.draw(G, pos)
plt.show()
口頭で補足すると
n個のノード、 m個の枝のグラフを定義しています。
つまり、今回だと10個のノードを定義し、その中で20個の枝に対して0, 1の範囲内でランダムな数を割りあてノード間の重みを定義しているという意味合いになります。
実際につながっているノード間を可視化すると以下のようになります。

前処理として、上記のグラフ構造を対角成分のない上三角行列で表します。
アルゴリズム的に対角成分のない行列でないといけないことはないですが、おそらくコーディング上計算式が簡単になるのでこうしているのだと思います。
(対角成分を表したい(イジングモデル的に言うと線形項を表したい)場合にAWS Braketで実装しようとすると別途工夫がいるので次回の記事にでも述べようと思います。)
以下前処理のソースコードと可視化です。
# set Ising matrix
Jfull = nx.adjacency_matrix(G).todense()
Jfull = np.array(Jfull)
# get off-diagonal upper triangular matrix
J = np.triu(Jfull, k=1).astype(np.float64)
# plot Ising matrix
plt.figure(1, figsize=[7, 5])
sns.heatmap(J, annot=True, linewidths=.5, cmap="YlGnBu", annot_kws = {'alpha': 1})
plt.title('Ising distance matrix');
plt.tight_layout();

QAOAの実行準備
注意したいのはQAOAの本体は util_qaoa.pyで定義しているということです。
なので util_qaoa をインポートすることを忘れないでください。
Ansatzの説明
QAOAの流れの中で適用されるユニタリゲート群をAnsatzと呼びます。
どういう意図でこういった名前になっているかはわかりませんが、おそらくAnsatzというのはドイツ語で仮設という意味らしいので
QAOAにおいて基底状態を求めるのに適切なユニタリゲート群をパラメータを用いて仮定してアルゴリズムの中で求める。といった背景からそういった名前で呼ばれている気がします。
とりあえず、以下の式で示される $U_{x}(\beta_{p})U_{zz}(\gamma_{p}) \cdots U_{x}(\beta_{1})U_{zz}(\gamma_{1})$がAnsatzと呼ばれる認識で良いと思います。
|\beta, \gamma \rangle = U_{x}(\beta_{p})U_{zz}(\gamma_{p}) \cdots U_{x}(\beta_{1})U_{zz}(\gamma_{1}) |s\rangle
ではこういったAnsatzって実際に回路上ではどうなっているのか?
といったところがAWS Braketのサンプル上の
VISUALIZATION OF THE QAOA ANSATZで記述されています。
ソースコードが書かれていますが、どちらかというと気にしないといけないのは実際に目に見てわかる可視化部分です。サンプルコードを見ると結果として以下の二つの可視化が示されています。
一つ目は、ステップ数 ($p$) が1で $\gamma_1=0.2, \beta_1=0.6$
二つ目は、ステップ数 ($p$) が2で $\gamma_1=0.2, \beta_1=0.6, \gamma_2=0.4, \beta_2=0.8$です。
Printing test circuit:
T : |0|1| 2 | 3 |
q0 : -X-H-ZZ(0.2)-Rx(0.6)-
|
q1 : -X-H-ZZ(0.2)-Rx(0.6)-
T : |0|1| 2 | 3 |
Printing test circuit:
T : |0|1| 2 | 3 | 4 | 5 |
q0 : -X-H-ZZ(0.2)-Rx(0.6)-ZZ(0.4)-Rx(0.8)-
| |
q1 : -X-H-ZZ(0.2)-Rx(0.6)-ZZ(0.4)-Rx(0.8)-
T : |0|1| 2 | 3 | 4 | 5 |
実際のQAOAではこれらのパラメータを最適化しながらより良い(基底状態を求めるのに適した)回路を作っていくことで全体の最適化を行っていきます。
QAOAの実行
** QAOA SIMULATION ON LOCAL SCHROEDINGER SIMULATOR **にてQAOAの実行を行っています。
以下のソースコードはパラメータの調整を行っています。
##################################################################################
# set up hyperparameters
##################################################################################
# User-defined hypers
DEPTH = 3 # circuit depth for QAOA
SHOTS = 10 # number measurements to make on circuit
OPT_METHOD = 'Powell' # SLSQP, COBYLA, Nelder-Mead, BFGS, Powell, ...
# set up the problem
n_qubits = J.shape[0]
# initialize reference solution (simple guess)
bitstring_init = -1 * np.ones([n_qubits])
energy_init = np.dot(bitstring_init, np.dot(J, bitstring_init))
# set tracker to keep track of results
tracker = {
'count': 1, # Elapsed optimization steps
'optimal_energy': energy_init, # Global optimal energy
'opt_energies': [], # Optimal energy at each step
'global_energies': [], # Global optimal energy at each step
'optimal_bitstring': bitstring_init, # Global optimal bitstring
'opt_bitstrings': [], # Optimal bitstring at each step
'costs': [], # Cost (average energy) at each step
'res': None, # Quantum result object
'params': [] # Track parameters
}
# set options for classical optimization
options = {'disp': True, 'maxiter': 500}
# options = {'disp': True, 'ftol': 1e-08, 'maxiter': 100, 'maxfev': 50} # example options
ざっくり説明すると
DEPTHはユニタリゲートの繰り返し回数、つまり、前述したユニタリゲートを示す$p$の値になります。
SHOTSはパラメータを決定した後、測定する回数と同値ととらえていただければ良いです。
QAOAの流れでは「量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する」と記載しましたが、ここの部分でどこまでが量子でどこからが古典かが多少わかりにくくなります。
量子計算で行うのはあくまで、$|\beta, \gamma \rangle$の量子状態を求めるところまでです。
この後、観測することでたった一つのビット配列を古典コンピュータで表現することとなります。ここの観測されるビット配列は、量子回路で作られた$|\beta, \gamma \rangle$の量子状態に基づく確率で決まります。そのため、実際に複数回測定して測定結果を測定回数で割り算してあげることで期待値を求めることととなります。
(後述する utils_qaoa.pyのソースコード上にも表れてきます。)
OPT_METHODは古典最適化で使用する最適化手法です。(デフォルトはPowellになってます。)
n_qubitsは量子ビットの数、bitstring_init, energy_init は古典最適化で最初の状態を定義する必要があるのでとりあえず定義してあげます。(適切な定義方法がある気がしますが、本質ではないので割愛します。)
optionsのmaxiterはQAOAの繰り返し回数の最大値を示しています。
パラメータの推定回数と言い換えてもいいかもしれません。
以下でQAOAを実際に動かしています。
##################################################################################
# run QAOA optimization on graph
##################################################################################
print('Circuit depth hyperparameter:', DEPTH)
print('Problem size:', n_qubits)
# kick off training
start = time.time()
result_energy, result_angle, tracker = train(
device = device, options=options, p=DEPTH, ising=J, n_qubits=n_qubits, n_shots=SHOTS,
opt_method=OPT_METHOD, tracker=tracker, s3_folder=s3_folder, verbose=verbose)
end = time.time()
# print execution time
print('Code execution time [sec]:', end - start)
# print optimized results
print('Optimal energy:', tracker['optimal_energy'])
print('Optimal classical bitstring:', tracker['optimal_bitstring'])
上記によりQAOAを動かすことができます。
QAOA_braket.ipynbのサンプル上ではこれ以降は出力の説明や古典アルゴリズムとの比較を行っていたりするだけですので、説明は割愛します。
QAOA本体の utils_classical.pyの説明に入っていこうと思います。
utils_qaoa.py
では実際にQAOAの本体のソースコードに触れていこうかと思います。
Ansatzで使用する回路の定義
まずAnsatzで使用する回路を定義してあげる必要があります。特に注意しないといけないのはRigettiではZZ回路(とりあえずそう呼んでいますが、正式な呼び方かどうかはわかりません。)が用意されていないのでCNOTと$R_Z$回路を用いて自分で作ってあげる必要があります。(参考:Amazon Braket のゲート型量子コンピュータで指定できる量子回路)
(あくまでRigetti用です。IonQでは用意されているのでそれを使いましょう)
# function to implement ZZ gate using CNOT gates
def ZZgate(q1, q2, gamma):
"""
function that returns a circuit implementing exp(-i \gamma Z_i Z_j) using CNOT gates if ZZ not supported
"""
# get a circuit
circ_zz = Circuit()
# construct decomposition of ZZ
circ_zz.cnot(q1, q2).rz(q2, gamma).cnot(q1, q2)
return circ_zz
次に$U_{x}(\beta_{p})U_{zz}(\gamma_{p}) \cdots U_{x}(\beta_{1})U_{zz}(\gamma_{1})$で示される $U_{x}(\beta_{i})$と$U_{zz}(\gamma_{i})$を定義していきます。
AWS Braketでは$U_{x}(\beta_{i})$と$U_{zz}(\gamma_{i})$はそれぞれdriver、cost_circuitと定義しているようで、以下のようにソースコード上では定義されています。
driverは以下となります。
# function to implement evolution with driver Hamiltonian
def driver(beta, n_qubits):
"""
Returns circuit for driver Hamiltonian U(Hb, beta)
"""
# instantiate circuit object
circ = Circuit()
# apply parametrized rotation around x to every qubit
for qubit in range(n_qubits):
gate = Circuit().rx(qubit, 2*beta)
circ.add(gate)
return circ
cost_circuitは以下となります。
# helper function for evolution with cost Hamiltonian
def cost_circuit(gamma, n_qubits, ising, device):
"""
returns circuit for evolution with cost Hamiltonian
"""
# instantiate circuit object
circ = Circuit()
# get all non-zero entries (edges) from Ising matrix
idx = ising.nonzero()
edges = list(zip(idx[0], idx[1]))
# apply ZZ gate for every edge (with corresponding interation strength)
for qubit_pair in edges:
# get interaction strength from Ising matrix
int_strength = ising[qubit_pair[0], qubit_pair[1]]
# for Rigetti we decompose ZZ using CNOT gates
if device.name == 'Rigetti':
gate = ZZgate(qubit_pair[0], qubit_pair[1], gamma*int_strength)
circ.add(gate)
# classical simulators and IonQ support ZZ gate
else:
gate = Circuit().zz(qubit_pair[0], qubit_pair[1], angle=2*gamma*int_strength)
circ.add(gate)
return circ
※以下「再開」部分まで少し深めの話なので飛ばしても大丈夫です。興味ある方だけ読んでください。
driverは特に気にする点はありませんが、cost_circuitでは注意が必要です。
前述したとおり、今回定義した最適化モデルは線形項が含まれていません。そして、対角成分も含まれていません。
線形項を含めたい場合、このcost_circuit関数の引数に新たに線形項を示す変数を定義してそれに対する演算を行う必要があります。
また、cost_circuitに引数として定義しているisingに対角成分を無理やり入れてしまうとゲート定義の際にエラーを起こしてしまいます。
対角成分は$z_iz_i$と示されますが、量子複製不能原理により同じビット同士の演算は行うことができません。
そのため、対角成分の演算はできないことに注意してください。
(${-1, 1}$イジングモデルだと対角成分はありませんが、${0,1}$モデルだと対角成分を定義できるので注意が必要です。)
${0,1}$モデルで対角成分の計算を行う方法、もしくは${-1, 1}$イジングモデルで線形項を含める方法は別記事で説明しようと思いますのでまた参考にしてみてください。
※再開
では、driverとcost_circuitを定義できたので全体の回路を定義しましょう。
# function to build the QAOA circuit with depth p
def circuit(params, device, n_qubits, ising):
"""
function to return full QAOA circuit; depends on device as ZZ implementation depends on gate set of backend
"""
# initialize qaoa circuit with first Hadamard layer: for minimization start in |->
circ = Circuit()
X_on_all = Circuit().x(range(0, n_qubits))
circ.add(X_on_all)
H_on_all = Circuit().h(range(0, n_qubits))
circ.add(H_on_all)
# setup two parameter families
circuit_length = int(len(params) / 2)
gammas = params[:circuit_length]
betas = params[circuit_length:]
# add QAOA circuit layer blocks
for mm in range(circuit_length):
circ.add(cost_circuit(gammas[mm], n_qubits, ising, device))
circ.add(driver(betas[mm], n_qubits))
return circ
まず初期状態を定義しています。
今回は $|-\rangle^{\otimes n} $を初期状態としていますが、QAOAの流れで示した通り、$|+\rangle^{\otimes n} $を初期状態としても問題ありません。
Xゲートの基底状態である量子状態を初期状態とすれば何でも大丈夫です。参考
目的関数
QAOAでは量子回路を適用してより最適なパラメータ $\beta, \gamma$ を求めることで最適解を求めていきます。
これはつまり、量子回路を適用することによって得られた結果を目的関数値とし、それを最適化していくこととなります。
もう少し詳しく言うと、量子ゲートを適用して複数回観測し、観測結果に基づいて期待値を求めます。
それを目的関数値として最適化することとなります。
ということなので目的関数値 objective_functionを定義します。
AWS Braketの関数では少し長めのコードになっているので一つ一つ説明していきます。
重要な変数
- params: パラメータ$\beta, \gamma$を持つ変数
- device: 適用する実機 or シミュレータ(デバイス識別子)
- ising: イジングモデル n × n 行列(対角成分のない上三角行列)
- n_shots: ショット数
- tracker: 結果や過程等の様々な変数を保存していく場所、主に古典最適化のために使う想定
- s3_folder: s3の保存先
- verbose: 出力するかどうか
主な流れ
1. qaoa_circuitに使用する回路を定義する
# get a quantum circuit instance from the parameters
qaoa_circuit = circuit(params, device, n_qubits, ising)
2. 量子コンピュータ or シミュレータを実行し、結果を保存する
# classically simulate the circuit
# execute the correct device.run call depending on whether the backend is local or cloud based
if device.name == 'DefaultSimulator':
task = device.run(qaoa_circuit, shots=n_shots)
else:
task = device.run(qaoa_circuit, s3_folder,
shots=n_shots, poll_timeout_seconds=3*24*60*60)
# get result for this task
result = task.result()
3. 観測値をマッピングする
今回は -1, 1で定義したので0 → -1に変更するマッピングする必要がありますが、0,1のでもうまくマッピングが行えればそれでも計算可能です。
# get metadata
metadata = result.task_metadata
# convert results (0 and 1) to ising (-1 and 1)
meas_ising = result.measurements
meas_ising[meas_ising == 0] = -1
4. すべての観測結果に対してエネルギーを求める
# get all energies (for every shot): (n_shots, 1) vector
all_energies = np.diag(np.dot(meas_ising, np.dot(ising, np.transpose(meas_ising))))
4. 最適値を更新する
# find minimum and corresponding classical string
energy_min = np.min(all_energies)
tracker['opt_energies'].append(energy_min)
optimal_string = meas_ising[np.argmin(all_energies)]
tracker['opt_bitstrings'].append(optimal_string)
# store optimal (classical) result/bitstring
if energy_min < tracker['optimal_energy']:
tracker.update({'optimal_energy': energy_min})
tracker.update({'optimal_bitstring': optimal_string})
6. 期待値を求めパラメータなどの更新を行う
# store global minimum
tracker['global_energies'].append(tracker['optimal_energy'])
# energy expectation value
energy_expect = np.sum(all_energies) / n_shots
if verbose:
print('Minimal energy:', energy_min)
print('Optimal classical string:', optimal_string)
print('Energy expectation value (cost):', energy_expect)
# update tracker
tracker.update({'count': tracker['count']+1, 'res': result})
tracker['costs'].append(energy_expect)
tracker['params'].append(params)
以上が古典で量子回路のパラメータを最適化していくプロセスとなります。
初期値の定義とインターフェース
パラメータの初期値を定義したり、別のプログラムから関数を呼び出すためのインターフェースとして train関数が定義されています。
こちらはパラメータの初期値を定義して、最適化関数を呼び出す程度のことしか行っていないため、割愛させていただきます。
まとめ
以上より、QAOAを実際に動かすために最低限必要な実装をAWSBraketのコードを見ながら解説していきました。
本文でも少しふれましたが、こちらはあくまでAWS Braketで公開されているサンプルコードを何も手を付けずに説明したものとなります。
なのでもう少し応用的な内容もやろうと思えばいくつかやれることがあるので
次回の記事では少し応用的な内容に触れていければと思っています。