この記事について
最近量子コンピューティングを勉強しているのですが、ゲート型の量子コンピュータを使ったQAOAの回路設計の話をするときにいつもうまく説明できないので一旦丁寧に計算しながらまとめていこうかと思います。
流れとしては
- ハミルトニアン(イジングハミルトニアン)の表し方を計算しながら示す
- ハミルトニアンの基底状態の求め方を示す
- 基底状態を求める際の回路設計を計算しながら作る
といった流れで説明していこうかと思います。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
ハミルトニアン(イジングハミルトニアン)の表し方
ハミルトニアンの定式化
そもそもQAOAにかかわらず多くの最適化問題は以下のイジングモデルという表し方であらわすことができます。
C(z) = \sum_{i=1}^n\sum_{j=1}^i C_{ij}z_iz_j + \sum_{i=1}^n B_iz_i
ここで $z_i$は {-1,1} で定義され $C_{ij}, B_{i}$ はそれぞれ定数を示します。
最小化問題であれば、上記$C(z)$を最小化すれば良いし、最大化問題であれば、最大化すれば良いということになります。
一般的には最小化問題として解かれるので今回も最小化問題として解くことを考えます。
では、さっそく量子の世界で考えたときに上記の問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = \sum_{i=1}^n\sum_{j=1}^i J_{ij}Z_iZ_j + \sum_{i=1}^n h_iZ_i
ここで $n$ はスピンをもつ粒子の数、$Z_i$ は $i$番目の粒子のスピンの$z$軸方向の成分を表します。
$z$軸方向の成分と簡単に書いてはいますが、実はそこまで簡単な話ではなく実際こちら物理量を示しているため、演算子であらわされます。(詳しくはこちら)
今回の使用する演算子は表記通り $Z$ 演算子です。かなり簡単めに説明すると $i$番目の粒子 = $i$番目の量子ビットであり、$Z|0\rangle = |0\rangle, Z|1\rangle = -|1\rangle$ なので、$|0\rangle$は $+z$方向を向いている状態、$|1\rangle$は$-z$方向を向いている状態を表しています。
つまり、古典で$0$を測定したとき、$1$と対応づけ、$1$を測定したとき、$-1$と対応づけることができそうです。
(逆でも良いですし、今回はZ測定で考えていますが、逆向きを測定できさえすればX測定前提で定式化もできそう?等思ってしまいますがそれは考えないことにします。誰か教えてください。)
ここまでだと何となくパウリ演算子$Z$を用いることで何となくハミルトニアンを定義し、基底状態を求め、観測することで最適な値を求めることができそうだ。
ということがわかるようなわからないような気がするので、実際に具体例を示して計算しながらやっていこうかと思います。
QAOAのアルゴリズム手順
以降でまず行おうと思っているのはあくまで「イジングハミルトニアンってパウリ演算子 $Z$であらわしても問題ないよね。」といったことを示していこうかと思っていますが、QAOAとの位置づけを明確にしておくことで少し理解が深まるかと思いますのでまずは具体例を示す前に一度QAOAのアルゴリズムの手順を示しておこうかと思います。
以下QAOAの手順となります。
- 重ね合わせ状態$|s\rangle = |+\rangle^{\otimes n}$を作る。
- パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$をかけていき、状態$|\beta, \gamma \rangle$を得る。
- 量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する
- $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。
- 最適解 $\beta^{ * }$,$\gamma^{ * }$を得るまで1~4を繰り返す。
- $|\beta^{ * } , \gamma^{ * } \rangle$ をZ基底で測定し、良さそうな測定結果を解として出力する。
QAOAではとくに「2~4」で示される手順によってエネルギー期待値を最小にする量子状態を求めにいきます。
なので今回具体例を用いて行おうとしているのはある意味「2~4」を手計算で無理やり計算して自分で「4.」のエネルギー期待値を求めてやろうというアプローチです。
具体例①:2量子ビットで考える
まずは問題の定義を行います。手計算で行っていくのにあまり難しい問題にはしたくないので、2ビットで表現される以下の問題を考えます。
C(z) = z_1z_0 + z_1
上記の問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = Z_1Z_0 + Z_1
$Z_0Z_1$は0番目と1番目の量子ビットの相互作用なので、0番目の量子ビットと1番目の量子ビットのそれぞれにパウリ演算子 $Z$ を作用させたテンソル積で表すことができ、$Z_1$は0番目の量子ビットに恒等変換 $I$を作用させ、1番目の量子ビットにパウリ演算子$Z$を作用させたテンソル積で示すことができます。
$|0\rangle$は $+z$方向を向いている状態、$|1\rangle$は$-z$方向を向いている状態を表しています。
古典での観測値とどう対応させるかはテンソル積の順序や定義する量子ビットの順序などに関わってくるのであまり詳しくは書きませんが注意が必要です。
(ちなみにこの計算やっている途中で私も混乱しました。)
今回は個人的に計算しなれている$|0\rangle$を$1$と対応させ、$|1\rangle$を$-1$に対応させていきます。
つまり上記$\hat{H}$は以下のように示すことができます。
\hat{H} = Z_1 \otimes Z_0 + Z_1 \otimes I_0
こちらのイジングハミルトニアンを手計算していきます。
\hat{H} = Z_1 \otimes Z_0 + Z_1 \otimes I_0 =
\begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix}
+ \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix}
\\
= \begin{bmatrix} 1&0&0&0 \\ 0&-1&0&0 \\ 0&0&-1&0 \\ 0&0&0&1 \end{bmatrix}
+ \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&-1&0 \\ 0&0&0&-1 \end{bmatrix}
= \begin{bmatrix} 2&0&0&0 \\ 0&0&0&0 \\ 0&0&-2&0 \\ 0&0&0&0 \end{bmatrix}
とりあえず以下の4つの状態を用意します。
\psi_{00} = |00\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \psi_{01} = |01\rangle = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \end{bmatrix},
\psi_{10} = |10\rangle = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \end{bmatrix}, \psi_{11} = |11\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}.
エネルギー期待値 $E = \langle \psi |\hat{H}|\psi \rangle$ を求めると。
E_{00} = \langle \psi_{00} |\hat{H}|\psi_{00} \rangle = 2, \\
E_{01} = \langle \psi_{01} |\hat{H}|\psi_{01} \rangle = 0, \\
E_{10} = \langle \psi_{10} |\hat{H}|\psi_{10} \rangle = -2, \\
E_{11} = \langle \psi_{11} |\hat{H}|\psi_{11} \rangle = 0.
なので上記よりエネルギー期待値を最小にする量子状態が $ \psi_{10} = |10\rangle $ であることがわかります。
これは0量子ビット目は $|0\rangle$ を示しており、1量子ビット目は $|1\rangle$ を示しているので
古典で観測すると$z_0 = 1, z_1 = -1$ に対応しており、結果として古典の世界で定義される以下のコスト関数を最小化することがわかります。
C(z) = z_1z_0+ z_1 = (-1) * 1 + (-1) = -2
ちなみに検算も兼ねてそれぞれ古典で測定すると仮定すると以下のように表されます。
\psi_{00} : z_1 = 1, z_0 = 1, \\
\psi_{01} : z_1 = 1, z_0 = -1, \\
\psi_{10} : z_1 = -1, z_0 = 1, \\
\psi_{11} : z_1 = -1, z_0 = -1.
それぞれのコストを計算すると以下の通りになり上記の期待値計算と一致するのがわかると思います。
\psi_{00} : z_1 = 1, z_0 = 1 : C(z) = z_1z_0+ z_1 = 1 * 1 + 1 = 2, \\
\psi_{01} : z_1 = 1, z_0 = -1 : C(z) = z_1z_0+ z_1 = 1 * -1 + 1 = 0, \\
\psi_{10} : z_1 = -1, z_0 = 1 : C(z) = z_1z_0+ z_1 = (-1) * 1 + (-1) = -2, \\
\psi_{11} : z_1 = -1, z_0 = -1 : C(z) = z_1z_0+ z_1 = (-1) * (-1) + (-1) = 0.
具体例②:3量子ビットで考える
ちょっとだけ難易度を上げて3ビットで表現される以下の問題を考えます。
C(z) = z_2z_1z_0 + z_1 + z_2
上記の問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = Z_2Z_1Z_0 + Z_1 + Z_2
具体例①と同様の考えで上記イジングハミルトニアンは以下の通りで示すことができます。
\hat{H} = Z_2 \otimes Z_1 \otimes Z_0 + I_2 \otimes Z_1 \otimes I_0 + Z_2 \otimes I_1 \otimes I_0
ちょっと長くなりそうなので一つ一つ計算してみます。
Z_2 \otimes Z_1 \otimes Z_0 = \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} = \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0&0&0 \\ 0&-1&0&0 \\ 0&0&-1&0 \\ 0&0&0&1 \end{bmatrix} \\
= \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&-1&0&0&0&0&0&0 \\ 0&0&-1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&-1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix}
I_2 \otimes Z_1 \otimes I_0 = \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} = \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \otimes \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&-1&0 \\ 0&0&0&-1 \end{bmatrix} \\
= \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&-1&0&0&0&0&0 \\ 0&0&0&-1&0&0&0&0 \\ 0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&-1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix}
Z_2 \otimes I_1 \otimes I_0 = \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} \otimes \begin{bmatrix} 1&0\\ 0&1 \end{bmatrix} = \begin{bmatrix} 1&0\\ 0&-1 \end{bmatrix} \otimes \begin{bmatrix} 1&0&0&0 \\ 0&1&0&0 \\ 0&0&1&0 \\ 0&0&0&1 \end{bmatrix} \\
= \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&-1&0&0&0 \\ 0&0&0&0&0&-1&0&0 \\ 0&0&0&0&0&0&-1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix}
以上より、イジングハミルトニアンは以下の通りで表されます。
\hat{H} = Z_2 \otimes Z_1 \otimes Z_0 + I_2 \otimes Z_1 \otimes I_0 + Z_2 \otimes I_1 \otimes I_0 \\
= \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&-1&0&0&0&0&0&0 \\ 0&0&-1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&-1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix}
+ \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&-1&0&0&0&0&0 \\ 0&0&0&-1&0&0&0&0 \\ 0&0&0&0&1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&-1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix}
+ \begin{bmatrix} 1&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&-1&0&0&0 \\ 0&0&0&0&0&-1&0&0 \\ 0&0&0&0&0&0&-1&0 \\ 0&0&0&0&0&0&0&-1 \end{bmatrix} \\
= \begin{bmatrix} 3&0&0&0&0&0&0&0 \\ 0&1&0&0&0&0&0&0 \\ 0&0&-1&0&0&0&0&0 \\ 0&0&0&1&0&0&0&0 \\ 0&0&0&0&-1&0&0&0 \\ 0&0&0&0&0&1&0&0 \\ 0&0&0&0&0&0&-1&0 \\ 0&0&0&0&0&0&0&-3 \end{bmatrix}
以下の8つの状態を用意します。
\psi_{000} = |000\rangle = \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},
\psi_{001} = |001\rangle = \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},
\psi_{010} = |010\rangle = \begin{bmatrix} 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix},
\psi_{011} = |011\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}, \\
\psi_{100} = |100\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \\ 0 \end{bmatrix},
\psi_{101} = |101\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \\ 0 \end{bmatrix},
\psi_{110} = |110\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \\ 0 \end{bmatrix},
\psi_{111} = |111\rangle = \begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}.
エネルギー期待値 $E = \langle \psi |\hat{H}|\psi \rangle$ を求めると。
E_{000} = \langle \psi_{000} |\hat{H}|\psi_{000} \rangle = 3, \\
E_{001} = \langle \psi_{001} |\hat{H}|\psi_{001} \rangle = 1, \\
E_{010} = \langle \psi_{010} |\hat{H}|\psi_{010} \rangle = -1, \\
E_{011} = \langle \psi_{011} |\hat{H}|\psi_{011} \rangle = 1, \\
E_{100} = \langle \psi_{100} |\hat{H}|\psi_{100} \rangle = -1, \\
E_{101} = \langle \psi_{101} |\hat{H}|\psi_{101} \rangle = 1, \\
E_{110} = \langle \psi_{110} |\hat{H}|\psi_{110} \rangle = -1, \\
E_{111} = \langle \psi_{111} |\hat{H}|\psi_{111} \rangle = -3,
なので上記よりエネルギー期待値を最小にする量子状態が $ \psi_{111} = |111\rangle $ であることがわかります。
これは0,1,2量子ビット目すべて $|1\rangle$ を示しており、古典で観測すると$z_0 = z_1 = z_2 = -1$ に対応しており、結果として古典の世界で定義される以下のコスト関数を最小化することがわかります。
C(z) = z_2z_1z_0+ z_1 + z_2 = (-1) * (-1) * (-1) + (-1) + (-1) = -3
2量子ビットの時と同様に検算も兼ねてそれぞれ古典で測定すると仮定すると以下のように表されます。
\psi_{000} : z_2 = 1, z_1 = 1, z_0 = 1, \\
\psi_{001} : z_2 = 1, z_1 = 1, z_0 = -1, \\
\psi_{010} : z_2 = 1, z_1 = -1, z_0 = 1, \\
\psi_{011} : z_2 = 1, z_1 = -1, z_0 = -1, \\
\psi_{100} : z_2 = -1, z_1 = 1, z_0 = 1, \\
\psi_{101} : z_2 = -1, z_1 = 1, z_0 = -1, \\
\psi_{110} : z_2 = -1, z_1 = -1, z_0 = 1, \\
\psi_{111} : z_2 = -1, z_1 = -1, z_0 = -1.
それぞれのコストを計算すると以下の通りになり上記の期待値計算と一致するのがわかると思います。
\psi_{000} : z_2 = 1, z_1 = 1, z_0 = 1 : C(z) = z_2z_1z_0+ z_1 + z_2 = 1 * 1 * 1 + 1 + 1 = 3, \\
\psi_{001} : z_2 = 1, z_1 = 1, z_0 = -1 : C(z) = z_2z_1z_0+ z_1 + z_2 = 1 * 1 * (-1) + 1 + 1 = 1, \\
\psi_{010} : z_2 = 1, z_1 = -1, z_0 = 1 : C(z) = z_2z_1z_0+ z_1 + z_2 = 1 * (-1) * 1 + (-1) + 1 = -1, \\
\psi_{011} : z_2 = 1, z_1 = -1, z_0 = -1 : C(z) = z_2z_1z_0+ z_1 + z_2 = 1 * (-1) * (-1) + (-1) + 1 = 1, \\
\psi_{100} : z_2 = -1, z_1 = 1, z_0 = 1 : C(z) = z_2z_1z_0+ z_1 + z_2 = (-1) * 1 * 1 + 1 + (-1) = -1, \\
\psi_{101} : z_2 = -1, z_1 = 1, z_0 = -1 : C(z) = z_2z_1z_0+ z_1 + z_2 = (-1) * 1 * (-1) + 1 + (-1) = 1, \\
\psi_{110} : z_2 = -1, z_1 = -1, z_0 = 1 : C(z) = z_2z_1z_0+ z_1 + z_2 = (-1) * (-1) * 1 + (-1) + (-1) = -1, \\
\psi_{111} : z_2 = -1, z_1 = -1, z_0 = -1 : C(z) = z_2z_1z_0+ z_1 + z_2 = (-1) * (-1) * (-1) + (-1) + (-1) = -3.
以上から初めの方で紹介したように
量子の世界で考えたときに最適化問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できる。
\hat{H} = \sum_{i=1}^n\sum_{j=1}^i J_{ij}Z_iZ_j + \sum_{i=1}^n h_iZ_i
そして、古典で$0$を測定したとき、$1$と対応づけ、$1$を測定したとき、$-1$と対応づけることができそうです。
というということが実際の計算によりわかったかと思います。
ハミルトニアンの基底状態の求め方
上記計算を行ったことによりもしかするとハミルトニアンのエネルギー期待値を最小化するのって意外と簡単では?という疑問を持った方もいるかもしれません。
この疑問に対する答えはノーです。
上記計算において計算機上で実現するにはいくつか問題があります。
わかりやすい話でいうと今回の具体例の計算ではとりあえずすべてのビット列を表現しそれに基づきエネルギー期待値を計算しています。
そしてその中で最小のものを選ぶという方法で計算を行いました。
これが 100 ビットを必要とする最小化問題だったと仮定しましょう。
表現しないといけないビット列は $2^{100}$ となることが容易に分かると思います。
そのため、量子コンピュータの重ね合わせの原理、もつれの状態の作成、シュレディンガーの方程式等、様々な物理法則を応用することになります。
概要だけ述べると「QAOAのアルゴリズム手順」でも述べた通り、ある量子状態から断続的にユニタリゲートを適用することでエネルギー期待値を最小にする量子回路をパラメータ調整しながら作成していきます。
そうすることで最終的にはエネルギー期待値を最小にする量子回路、そしてその回路を適用して同様にエネルギー期待値を最小にする量子状態を獲得できます。
おさらいですが、「QAOAのアルゴリズム手順」では以下のように述べました。
- 重ね合わせ状態$|s\rangle = |+\rangle^{\otimes n}$を作る。
- パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$をかけていき、状態$|\beta, \gamma \rangle$を得る。
- 量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する
- $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。
詳しくは
こちらの記事を見ていただけると幸いです。
一方で、上記の手順もしくは上記の記事を見てみると一点疑問が浮かんでくるかと思います。
パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$ ってどうやって表すの?という疑問です。
その疑問に答えるため、
基底状態を求める際の回路設計を計算しながら作る
ということをやっていこうと思います。
基底状態を求める際の回路設計を計算しながら作る
まずパラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$が何なのかですが、
こちらの記事を見ていただけると
U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)}, \\
U_X(\beta_{i}) = e^{-i\beta_{i} \sum_{j=1}^n X_j}.
と示されているのがわかります。
同じような考え方で $(\beta_{i})$も語ることができるので今回は$U_C(\gamma_{i})$にのみ焦点を絞って議論していきます。
具体例③:1量子ビットで考える
今回はまずは1量子ビットで考えることをやっていこうと思います。
以下のハミルトニアンを定義します。
C(z) = z_0
上記の問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = Z_0
このイジングハミルトニアン$\hat{H}$は$U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)}$における$C(Z)$と対応しているため、
U_C(\gamma_{i}) = e^{-i\gamma_{i} Z_0}.
と示すことができます。
これをある量子状態に適用することで基底状態を求めに行くのですが、
ではこれをどう回路上で表現するかです。計算しましょう。
とはいえ、実は熟練者だと$R_Z(2\gamma_{i})$であることがすぐにわかるかと思います。
一方で素人目線ですとなんでそうなるのかが意味が分からないのでそれを示していきます。
前提となる知識として 行列の指数関数に関する知識が必要です。
Googleで「オイラーの公式 行列」等で調べたら出てきます。
行列の指数関数は以下の性質を持ちます。
A = \begin{bmatrix} \lambda_1&0&0&...&0 \\ 0&\lambda_2&0&...&0 \\ ...&...&...&...&... \\ 0&0&0&...&\lambda_n \end{bmatrix}
のとき
e^{Ax} = \begin{bmatrix} e^{\lambda_1x}&0&0&...&0 \\ 0&e^{\lambda_2x}&0&...&0 \\ ...&...&...&...&... \\ 0&0&0&...&e^{\lambda_nx} \end{bmatrix}
と示すことができます。
なんでこうなるかという証明はこちらを参考にしてみてください。
本題に戻ります。
上記法則を用いると、
e^{-i\gamma_{i} Z_0} = \begin{bmatrix} e^{-i\gamma_{i}}&0 \\
0&e^{i\gamma_{i}} \end{bmatrix} = R_{Z_0}(2\gamma_{i})
となることがわかります。
(ほとんど計算しなくてもいけた。オイラー先生偉大!!)
具体例④:2量子ビットで考える
つぎは2量子ビットで考えてみます。
以下のハミルトニアンを定義します。
C(z) = z_1z_0
上記の問題は以下のイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = Z_1Z_0
このイジングハミルトニアン$\hat{H}$は$U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)}$における$C(Z)$と対応しているため、
U_C(\gamma_{i}) = e^{-i\gamma_{i} Z_1Z_0}.
と示すことができます。
Z_1 \otimes Z_0 = \begin{bmatrix} 1&0&0&0 \\ 0&-1&0&0 \\ 0&0&-1&0 \\ 0&0&0&1 \end{bmatrix}
なので具体例④のように考えると
e^{-i\gamma_{i} Z_1Z_0} = \begin{bmatrix} e^{-i\gamma_{i}}&0&0&0 \\ 0&e^{i\gamma_{i}}&0&0 \\ 0&0&e^{i\gamma_{i}}&0 \\ 0&0&0&e^{-i\gamma_{i}} \end{bmatrix} \\
= \begin{bmatrix} 1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \\ 0&1&0&0 \end{bmatrix}
\begin{bmatrix} e^{-i\gamma_{i}}&0&0&0 \\ 0&0&0&e^{-i\gamma_{i}} \\ 0&0&e^{i\gamma_{i}}&0 \\ 0&e^{i\gamma_{i}}&0&0 \end{bmatrix} \\
= \begin{bmatrix} 1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \\ 0&1&0&0 \end{bmatrix}
\begin{bmatrix} e^{-i\gamma_{i}}&0&0&0 \\ 0&e^{i\gamma_{i}}&0&0 \\ 0&0&e^{i\gamma_{i}}&0 \\ 0&0&0&e^{-i\gamma_{i}} \end{bmatrix}
\begin{bmatrix} 1&0&0&0 \\ 0&0&0&1 \\ 0&0&1&0 \\ 0&1&0&0 \end{bmatrix} \\
= CX_{0, 1} (R_{Z_1}(2\gamma_{i}) \otimes I_0) CX_{0, 1} \\
= CX_{0, 1} R_{Z_1}(2\gamma_{i}) CX_{0, 1}.
$CX$はコントロールノット(制御Xゲートを示します。)
※計算順序に注意してください。(今回は $|10 \rangle$ でいうと0が0番目の量子ビット、1が1番目の量子ビットなのでCNOTは上記の通り定義されます。間違えやすいし、私も間違えていたので…)
上記より2量子ビットの表現を行うことができました。
ここまでくると3量子ビット表現もやってみたいところですが、やめておきましょう。
量子ゲート回路
せっかくなので最後に実際の回路図を示して終わりにしようかなと思います。
以下のイジングハミルトニアンで考えます。
\hat{H} = Z_1Z_0 + Z_0
上記イジングハミルトニアン$\hat{H}$は$U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)}$における$C(Z)$と対応しているため、
U_C(\gamma_{i}) = e^{-i\gamma_{i} (Z_1Z_0+Z_0)}.
実はこの状態だと回路に落とし込むことはできません。
なので上記式を変形する必要がありますが、いろいろごちゃごちゃしそうなので途中は省き(トロッター展開等を考えると)近似的に以下のように示すことができます。
U_C(\gamma_{i}) = e^{-i\gamma_{i} (Z_1Z_0+Z_0)} \approx e^{-i\gamma_{i} (Z_1Z_0)} \cdot e^{-i\gamma_{i} Z_0}.
具体例③、④で示した通りに計算すると、
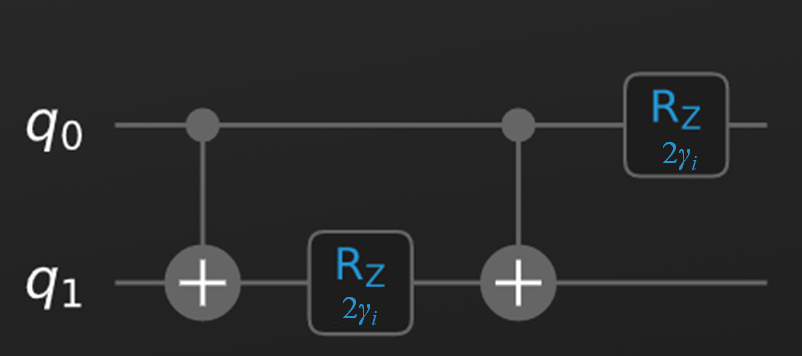
e^{-i\gamma_{i} (Z_1Z_0)}e^{-i\gamma_{i} Z_0} = CX_{0, 1} R_{Z_1}(2\gamma_{i}) CX_{0, 1} \cdot R_{Z_0}(2\gamma_{i})
となり、量子回路で表現できることがわかります。
そして、上記の回路を図示してみると以下の通りとなります。
最後に
今回は実際に手計算を行うことでQAOAでのハミルトニアンの定義や量子回路の表し方が正しいことを示してみました。
改めてあまり物理や数学に明るくない状態であっても手を動かせばそれなりに理解できるもんだなと感じることができたので
ぜひ量子コンピュータ難しいなと感じている人は手を動かして計算してみて確かにそうなるな。ということを認識していただければなと思います。