この記事について
量子コンピューティングを勉強している中でどう頑張ってもQAOAの説明をうまくできないので一つ一つ丁寧に説明するような記事を書いてみようと思いました。
理解が微妙なところもありますが、何か違うところがあればぜひご指摘いただきたいなという思いとともに今から量子コンピューティング(ゲート型)の勉強を始めようという方にはぜひご参考になればなと思っております。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
概要
QAOAとは、量子ゲート型で組み合わせ最適化問題を解くアルゴリズムです。
一般的に0-1整数計画問題は以下の定義で示されるイジングハミルトニアンのエネルギー期待値を最小化する問題に帰着できます。
\hat{H} = \sum_{i=1}^n\sum_{j=1}^i J_{ij}Z_iZ_j + \sum_{i=1}^n h_iZ_i
QAOAは量子断熱計算の考え方がベースとなっているとされていますが、良く目にする書籍や文献などでは意外と量子断熱計算ベースでの説明はされておらず、
- ハミルトニアンをトロッター分解できる。
- これは時間発展で示すことができる。
- 上記の考え方って量子断熱計算だよね。
といった説明のされ方が良くされています。特に違和感はない考え方ではありますが、量子断熱計算から考える考え方もあるようで、その辺が個人的に混乱を招いていたところだと思っていたので今回は
- 良く文献で見る説明のされ方
- 量子断熱計算から考える説明のされ方
といった二つのアプローチでQAOAを考えてみようかと思います。
特に二つ目の考え方は量子アニーリングをずっとやっていた方や最適化において焼きなまし法などを扱っていた方には理解しやすい考え方になっている気がします。
また、後者の考え方をできると最近でてきた問題に特化させた量子回路の設計 も考えやすくなるかと思います。
QAOA
本項で実際にQAOAの説明をしていきますが、上記でも述べている通り、まずは
- 良く文献で見る説明のされ方
をした後、
- 量子断熱計算から考える説明のされ方
をしていきます。
良く文献で見る説明のされ方
トロッター分解による量子ビットゲートの表し方
ある量子状態を作りたいとき、ユニタリ変換を断続的に行う量子シミュレーションを行うことである量子状態を実現させることができます。
(トロッター分解に基づいたダイナミクスシミュレーションといった言い方もするようです。参考:https://dojo.qulacs.org/ja/latest/notebooks/4.2_trotter_decomposition.html )
量子状態の時間発展はシュレディンガー方程式に従うため、
-i \frac{\partial }{\partial t} \mid \psi\rangle = \hat{H} \mid \psi\rangle
と書くことができ、ハミルトニアン $\hat{H}$ が時間に依存しない場合、
\mid \psi\rangle = e^{-i\hat{H}t}\mid\psi_0 \rangle
のように初期状態$\mid \psi_0 \rangle$からスタートして$e^{-i\hat{H}t}$を作用させた形であらわすことができます。
$n$量子ビットからなるイジングモデル(イジングハミルトニアン)を考えると$e^{-i\hat{H}t}$は
e^{-i\hat{H}t} = e^{-i(\sum_{i=1}^n\sum_{j=1}^i J_{ij}Z_iZ_j)t} = e^{-i(Z_1Z_2+Z_2Z_3...)t}
とあらわされますが、これでは量子回路で表現することができません。
なのでトロッター分解により
e^{-i\hat{H}t} = e^{-i(\sum_{i=1}^n\sum_{j=1}^i J_{ij}Z_iZ_j)t} = (e^{-i(Z_1Z_2+Z_2Z_3...)^{(t/M)}})^M \approx (e^{-i(Z_1Z_2)^{(t/M)}}e^{-i(Z_2Z_3)^{(t/M)}}...)^M
と分解できます。
つまり、2量子ビットゲートである$e^{-i(Z_1Z_2)^{(t/M)}}$の $nM$個の積で記述できました。(詳しくは別の記事を書く予定ですのでそちらを参考にしてください。)
問題の定義
$z = z_{1}z_{2}\cdots z_{n} \: (z_i =0,1)$ という$n$桁のビット列$z$に関して、コスト関数$C(z) = \sum_\alpha C_\alpha(z)$が最小になるような$z$を探す問題を考えます。イジングモデルで書ける最適化問題ならば$C(z)$は$z_iz_j$のような項から構成されています。
$n$ビットの量子系を用いてこの最小化問題を解きます。
$\beta = (\beta_{1}, \cdots \beta_{p}), \gamma = (\gamma_{1}, \cdots \gamma_{p})$ をパラメータとして、次のような量子状態を考えます。
|s\rangle = |+\rangle^{\otimes n} = \frac{1}{2^{n/2}} \sum_{z=0}^{2^{n}-1} |z\rangle, \\
|\beta, \gamma \rangle = U_X(\beta_{p}) U_C(\gamma_{p}) \cdots U_X(\beta_{1}) U_C(\gamma_{1}) |s\rangle.
ここで $|+\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$は$X$演算子の固有状態$X|+\rangle=|+\rangle$であり、 上記トロッター分解を考慮すると、$U_C(\gamma), U_X(\beta)$ は次のように定義されます。
U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)} = \prod_{\alpha} e^{-i\gamma_{i} C_{\alpha}(Z)}, \\
U_X(\beta_{i}) = e^{-i\beta_{i} \sum_{j=1}^n X_j} = \prod_{j =1}^n e^{-i\beta_{i} X_j}.
これは断熱量子計算で自明な基底状態(簡単な問題に対する基底状態)を持つ初期ハミルトニアンからコストハミルトニアンに時間発展させる $e^{-iHt}$を$p$ステップで変化させるトロッター分解に相当します。(と言われてもわからないので飛ばしがちになり、さらにわからなくなるので後述の別アプローチで説明していこうと思います。ここではとりあえず説明を続けていきます。)
ここで、$C(Z)$というのはビット列を引数にとる関数$C(z)$の入力にパウリ演算子$Z_1\cdots Z_n$を代入したものとなります。
QAOAでは、このような状態を用意したうえで、コストハミルトニアンのエネルギー期待値 $\langle{\bf \beta, \,\gamma}|C(Z)|{\bf \beta, \, \gamma}\rangle$ を最小にする$\beta$, $\gamma$を探索します。
QAOAアルゴリズムの手順
QAOAのアルゴリズムの手順は以下の通りです。
- 重ね合わせ状態$|s\rangle = |+\rangle^{\otimes n}$を作る。
- パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$をかけていき、状態$|\beta, \gamma \rangle$を得る。
- 量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する
- $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。
- 最適解 $\beta^{ * }$,$\gamma^{ * }$を得るまで1~4を繰り返す。
- $|\beta^{ * } , \gamma^{ * } \rangle$ をZ基底で測定し、良さそうな測定結果を解として出力する。(Z基底で測定することが重要。こちらを参考)
上記のような手順を踏むことで最適な解を獲得できます。
量子断熱計算から考える説明のされ方
上記のようにトロッター分解の説明をしていき、コストハミルトニアンを定義し、それっぽく初期ハミルトニアンも定義していき、トロッター分解を実際に行う&量子回路に落とし込むでQAOAの説明は行われます。
そして多くの場合、QAOAをとりあえず使用するにあたっては問題となることはないと思います。
一方で、量子断熱計算の考え方を知っていなければそもそも $|\beta, \gamma \rangle = U_X(\beta_{p}) U_C(\gamma_{p}) \cdots U_X(\beta_{1}) U_C(\gamma_{1}) |s\rangle$ の定義周りで訳が分からなくなるので量子断熱計算をベースにQAOAの説明をしていこうかと思います。
量子断熱計算
まず量子断熱計算が何かを説明していきます。
量子断熱計算においても以下のシュレディンガー方程式に従って系を変化させていくこととなります。
-i \frac{\partial }{\partial t} \mid \psi\rangle = \hat{H} \mid \psi\rangle
$\hat{H}$は時間に依存するハミルトニアンであり、系の状態変化はハミルトニアンに依存することがわかります。
そのため、量子断熱計算を考えるうえでこのように時間に依存するハミルトニアンの構成を考えることは重要で、量子断熱計算で扱うハミルトニアンは以下のように表現されます。
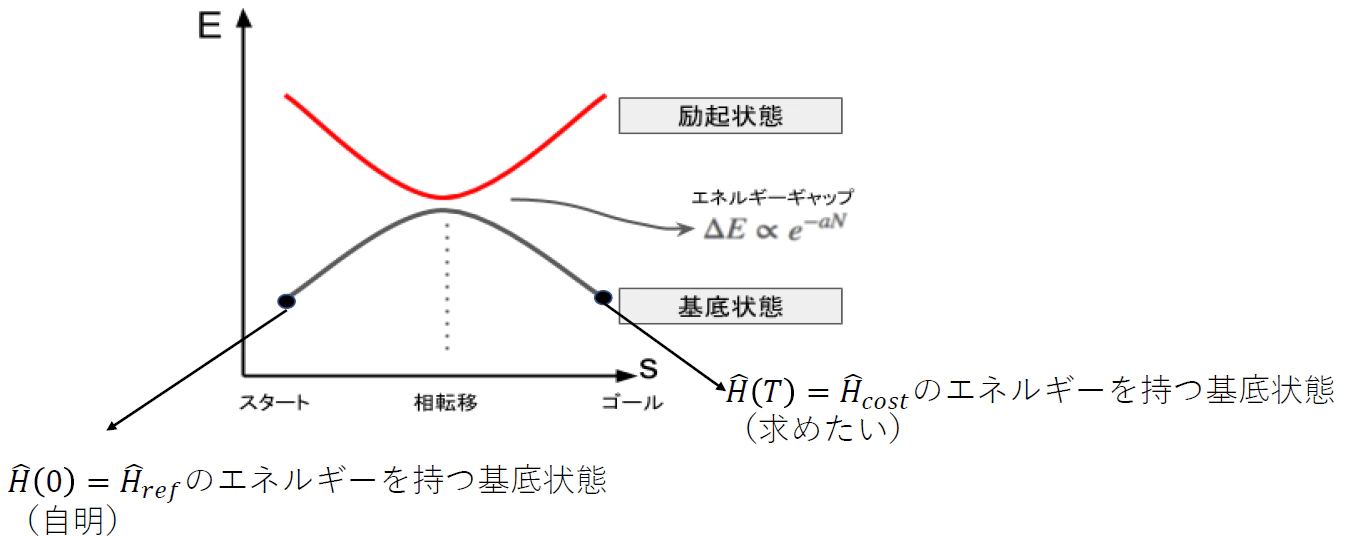
\hat{H} = \biggl( 1- \frac{t}{T} \biggr) \hat{H} _{ref} + \frac{t}{T} \hat{H} _{cost}
ここで $ \hat{H} _{cost} $ は終状態のハミルトニアン、つまり、最終的に欲しい結果を基底状態として持つコストハミルトニアンを示します。
$\hat{H}_{ref}$ は始状態のハミルトニアン(リファレンスハミルトニアンと呼ぶ)となります。
自明な基底状態を持つリファレンスハミルトニアン $\hat{H}_{ref}$ の基底状態から少しずつ変化させることによってほしい答えを得ます。
つまり、時間を0 → Tに変化させることによって求めたい計算結果を得ることができます。
引用:https://qiita.com/snhrhdt/items/ae55a94b25c06142528a
断続的なユニタリ変換
量子断熱計算の考え方から以下の断続的なユニタリ変換を導いていこうと思います。
U = U_X(\beta_{p}) U_C(\gamma_{p}) \cdots U_X(\beta_{1}) U_C(\gamma_{1}) (*)
量子断熱計算を離散的な時間ステップで考えていきます。
そのうえで、時間的な考え方をしていくため、先ほど示したハミルトニアンを明確に時間で示した
\hat{H}(t) = \biggl( 1- \frac{t}{T} \biggr) \hat{H} _{ref} + \frac{t}{T} \hat{H} _{cost}
と示すことにします。
このように示したときシュレディンガー方程式も以下のようにあらわされます。
-i \frac{\partial }{\partial t} \mid \psi\rangle = \hat{H}(t) \mid \psi\rangle
上記微分方程式の解は以下のようにあらわすことができます。
U(t)=\prod exp (-i \hat{H} (t) ∂t ) = exp(-i \hat{H}(t) ∂t) exp(-i\hat{H}(t-∂t)∂t)・・・・exp(-i \hat{H}(∂t)∂t) exp(-i \hat{H}(0)∂t)
ハミルトニアンは通常非可換なので、トロッター分解より、
exp(-i \hat{H}(∂t)∂t) \approx exp \bigl( -i(1-t)∂t \hat{H}_{ref} \bigr)
exp \bigl(-i t ∂t \hat{H} _{cost} \bigr)
とあらわすことができます。
ここで、$ \beta = (1-t)∂t , \gamma = t∂t $ と置きます。
つまり、上記 $U(t)$は
U(t) = exp(-i \beta _ {p} \hat{H} _{ref} ) exp(-i \gamma _{p} \hat{H} _{cost} ) ・・・・ exp(-i \beta _{1} \hat{H} _{ref}) exp(-i \gamma _{1} \hat{H} _{cost})
とあらわすことができます。
(引用:https://qiita.com/snhrhdt/items/ae55a94b25c06142528a )
こちらの式を$(*)$と見比べると、
U_C(\gamma_{i}) = exp(-i \gamma _{i} \color{red}{\hat{H} _{cost}}), \\
U_X(\beta_{i}) = exp(-i \beta _{i} \color{blue}{\hat{H} _{ref}}).
が対応していることがわかります。
U_C(\gamma_{i}) = e^{-i\gamma_{i} \color{red}{C(Z)}}, \\
U_X(\beta_{i}) = e^{-i\beta_{i} \color{blue}{\sum_{j=1}^n X_j}}.
なので、
\color{red}{\hat{H} _{cost} = C(Z)} \\
\color{blue}{\hat{H} _{ref} = \sum_{j=1}^n X_j}
だということもわかるかと思います。
以上が量子断熱計算から考える説明のされ方でした。
残りのアルゴリズムの手順などはいつも通りの説明となるので割愛させていただきます。
また、こちらの記事ではさらにふかぼって記載してたりするので是非見てみてください。
本記事を書くにあたってとても参考にさせていただきました。ありがとうございます。
最後に
今回は通常のQAOAの説明での断続的なユニタリ変換への帰着の説明と量子断熱計算の考え方からQAOAの断続的なユニタリ変換を説明する二つのアプローチを比較してみました。
特に量子断熱計算の方からの考え方から自明な基底状態を持つリファレンスハミルトニアン(初期ハミルトニアン)の存在が明確に分かったかと思います。
「自明な基底状態を持つ」という点がある意味重要な点で、これが問題に特化させた量子回路の設計(Quantum Alternating Operator Ansatz)の話につながっていきます。
また、こちらの記事も書いていこうと思いますのでよろしくお願いいたします。
参考にした記事や本、論文等
1量子ビットVQEを世界一簡単に書く 2020年2月Ver.
ハイゼンベルク猫像
時間発展演算子
指数函数の順序積
Quantum Native Dojo
QAOA - ゲート式量子コンピューターで最適化問題を解く近似アルゴリズム
量子コンピューティング 基本アルゴリズムから量子機械学習まで