はじめまして。株式会社Qnasysでインターンを行っているヒデトです。
QAOA(Quantum Approximate Optimization Algorithm)についての論文を読んだので、それについてまとめたいと思います。
読んだ論文
A Quantum Approximate Optimization Algorithm
https://arxiv.org/pdf/1411.4028.pdf
最初にQAOAを提案した論文
Unsupervised Machine Learning on a Hybrid Quantum Computer
https://arxiv.org/pdf/1712.05771.pdf
Rigettiという会社が実際に量子コンピュータでQAOAを実装したという報告論文
概要
量子ゲートで、組み合わせ最適化問題を解く近似アルゴリズムです。Quantum Adiabatic Algorithm(QAA・量子断熱計算)という考え方がベースとなっています。
アルゴリズムの性能は繰り返し回数pに依存しており、p=1,3正則グラフのMAX CUT問題で0.6924近似となります。
3正則とはグラフの全ての頂点に必ず枝が3本ついていることを意味しています。また0.6924近似というのは、最適値を1としたときに必ず0.6924の値以上の解が得られることを意味しています。
(MAXCUT問題については、下の方で詳しく述べています!)
QAA(量子断熱計算)とは?
量子力学ではある演算子で測定を行うと、その演算子の固有値のどれかが確率的に得られ、測定を行った系の状態がその固有値に対応する固有状態に変化します。
ということは、量子ゲートの最終的に求めたいqubit列も何かの演算子の固有状態になっているはずです。
そこで欲しい結果を基底状態として持つコストハミルトニアン(エネルギー演算子)
$$\hat{H}_{cost}$$
を作り、自明な基底状態を持つリファレンスハミルトニアン
$$\hat{H}_{ref}$$
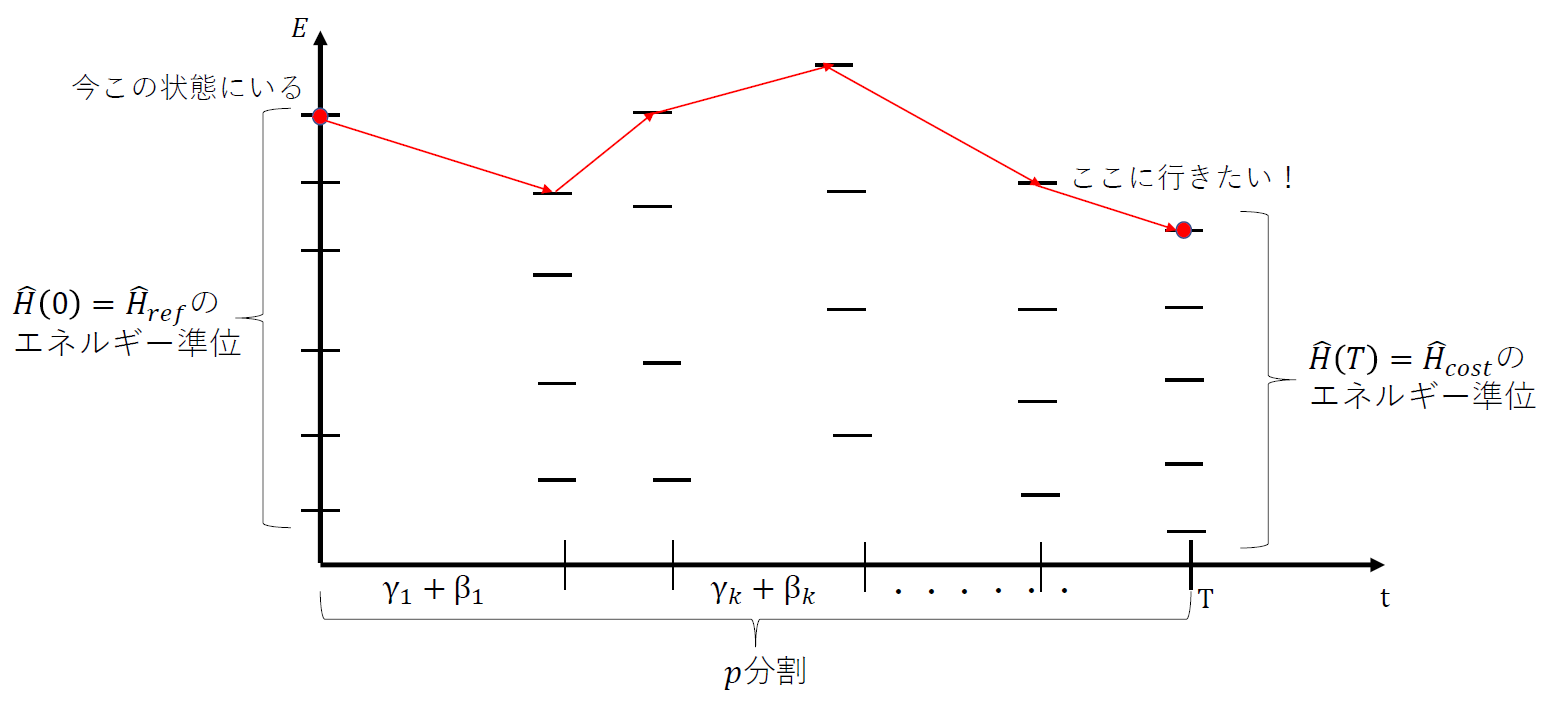
の基底状態から少しずつ変化させることによって、欲しい答えを得ます。
つまり全体のハミルトニアンを
$$ \hat{H} (t) = \biggl( 1- \frac{t}{T} \biggr) \hat{H} _{ref} + \frac{t}{T} \hat{H} _{cost} $$
とし、時間を0→Tと少しずつ変化させることによって、求めたい計算結果を得ることができます。
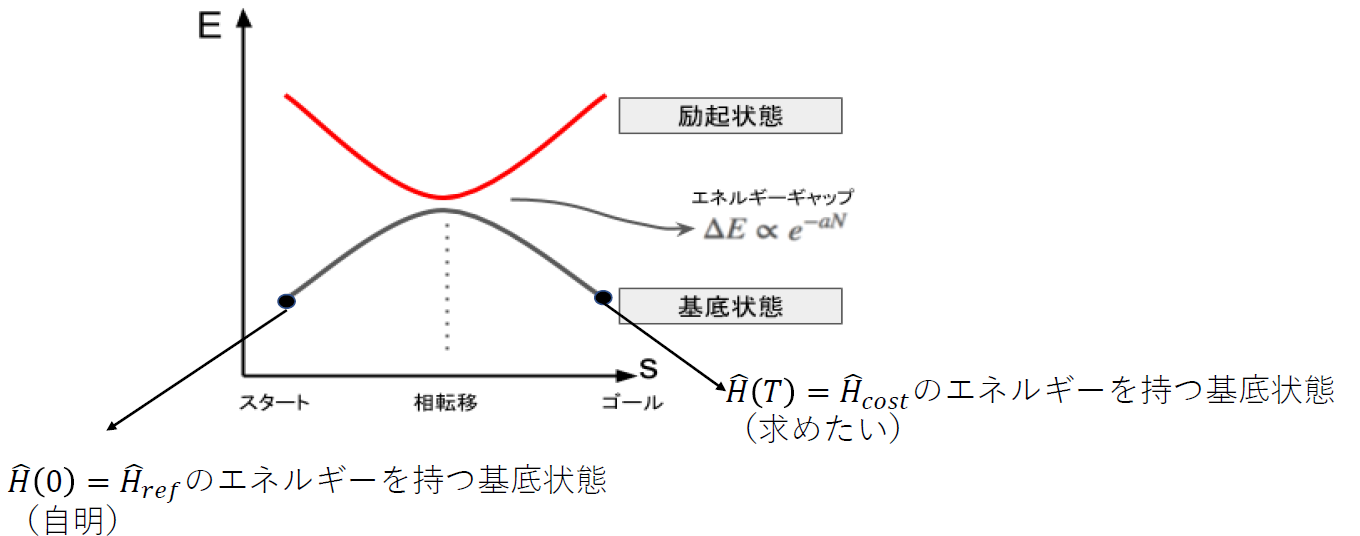
引用:https://qiita.com/YuichiroMinato/items/00148921f7c060674d8b
QAOA
先程のQAAを離散的に、自由な時間ステップで計算を行います。
ハミルトニアンによる時間発展を考えたいので、まずは以下のシュレディンガー方程式の解を考えましょう。
(ちなみにこの分野は扱う系が量子系であるので、$\hbar$はよく省略されています。)
$$-i \frac{\partial }{\partial t} |\psi> = \hat{H}(t) |\psi>$$
これの解は時間順積分より
$$ U(t)=exp \biggl( -i \int \hat{H} (t) ∂t \biggr)
= exp(-i \hat{H}(t) ∂t) exp(-i\hat{H}(t-∂t)∂t)・・・・exp(-i \hat{H}(∂t)∂t) exp(-i \hat{H}(0)∂t)$$
2つのハミルトニアンは通常非可換なので、トロッター展開より
$$ exp(-i \hat{H}(∂t)∂t) \approx exp \bigl( -i(1-t)∂t \hat{H}_{ref} \bigr)
exp \bigl(-i t ∂t \hat{H} _{cost} \bigr) $$
ここで
$$ \beta = (1-t)∂t , \gamma = t∂t $$
と置きます。
つまり、$ \hat{H}_{ref} $ の自明な基底状態$ |s>$ に
$$ U(t) = exp(-i \beta _ {p} \hat{H} _{ref} ) exp(-i \gamma _{p} \hat{H} _{cost} ) ・・・・ exp(-i \beta _{1} \hat{H} _{ref}) exp(-i \gamma _{1} \hat{H} _{cost}) $$
を作用させて、最適解に近づけます。
これを作用させた状態を
$$ | \boldsymbol{\gamma}, \boldsymbol{\beta} >$$
とします。
$\boldsymbol{\gamma}= \gamma _{1},・・・・,\gamma _{p}$ , $\boldsymbol{\beta}= \beta _{1},・・・・,\beta _{p}$ とします。
QAAでは、T(Total Run Time)を無限の極限を取れば最適解に収束します。
よってQAOAでは、p(繰り返し回数)を無限の極限を取ることによって最適解に収束すると考えられます。
γ,β,p は何を意味するのか?
QAAとの対応を考慮し、pは分割回数、γとβは分割の間隔に対応すると考えられます。
しかしながら無限回pを作用させることができるならまだしも、実際には有限回しか作用させることができません。
そうなってくると、実際にどこのエネルギー準位にたどり着くかはわからないわけです。
そこで、$\hat{H} _{cost}$の$| \gamma, \beta>$ おける期待値 $<\gamma, \beta| \hat{H} _{cost} | \gamma, \beta>$を最大化する問題を考えます。
これは$(\boldsymbol{\gamma}, \boldsymbol{\beta})$の値によって変わります。
すなわち、
$$max <\gamma, \beta| \hat{H} _{cost} | \gamma, \beta> $$
となる、$(\boldsymbol{\gamma}, \boldsymbol{\beta})$を探す問題に帰着できます。
なぜこうするか、なぜこれが良いのか?
組み合わせ最適化問題の制約式の数を$m$、与えられる変数の数を$n$とします。
以下の理由より、QAOAは古典アルゴリズムの性能を超える可能性があるのではないかと考えられます。
①$m$回程度の測定で、$<\gamma, \beta| \hat{H} _{cost} | \gamma, \beta>$近辺の測定値が得られる。
($<\gamma, \beta| \hat{H} _{cost} | \gamma, \beta>$の分散を計算することによって得られる。)
②$(\boldsymbol{\gamma}, \boldsymbol{\beta})$が$n,m$でなく、繰り返し回数$p$に依存する。
①より、良い$(\boldsymbol{\gamma}, \boldsymbol{\beta})$さえ求まれば$m$回程度の測定で良い近似解が得られることがわかります。
さらに②より、その$(\boldsymbol{\gamma}, \boldsymbol{\beta})$を求める作業も問題サイズの$n,m$に依存しません。
すなわち、大規模な問題が与えられても計算時間がさほど変わらないと考えられます。
アルゴリズム(QAOA)の性能
・2正則のMAXCUT問題において、pを増やしていけば近似値が1倍に近づくことを数値計算により確認したそうです。
・3正則のMAXCUT問題では、p=1で0.6924倍の近似値が得られることがこちらも数値計算より確認したそうです。
正則グラフって扱いやすいグラフなんですが、このアルゴリズムは正則グラフしか使えないの?っていう疑問が湧いてくると思います。
実際は任意のグラフで使うことができます。
実際に近似値を出す時に数値計算で求めているので、計算しやすい正則グラフが論文では例に出されています。
Regettiによる実装
以上のアルゴリズムをRegettiという会社が19qubitの量子ゲートを使って実装しています。
解く問題はMACUT問題という最適化問題です。
MAXCUT問題とは、あるグラフ(頂点と枝の集合)が与えられたときに頂点を2つの部分集合に分けます。このときに、両端の頂点が違う部分集合に属するような枝の数を最大化するような分け方を見つける問題となります。
この問題は機械学習のクラスタリングなどに使われており、NP完全の問題です。
以下が実際に解くMAXCUT問題のグラフになります。
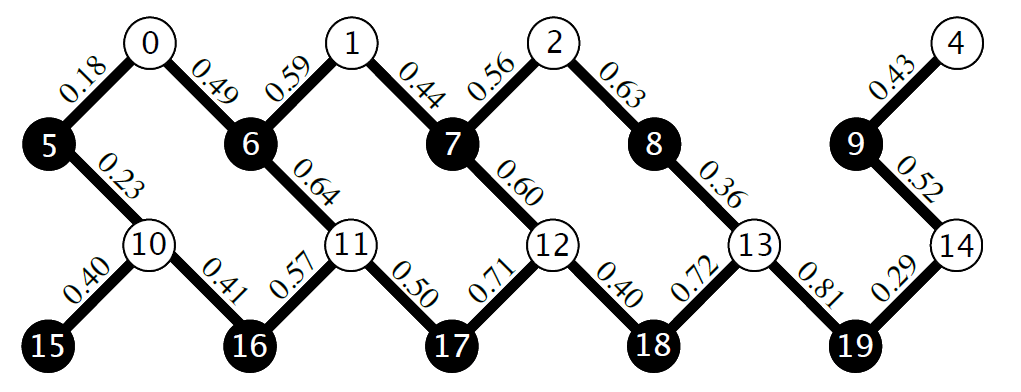
引用:https://arxiv.org/pdf/1712.05771.pdf
求めたいエネルギーを持つハミルトニアンは次のように表されます。
$$ \hat{H} _{cost} = -\frac{1}{2} \sum _{i,j} C _{ij} \bigl( 1- \hat{\sigma} ^{z} _{i} \hat{\sigma} ^{z} _{j} \bigr) $$
先頭に"-"がつけることによって、最大化の問題を最小化の問題に変えています。
これによって、求めたい状態は上記のハミルトニアンの基底状態となります。
また$C _{ij}$は枝の重み、その後の( )内は
「枝が張られている頂点が同じ集合なら0」
「違う集合に属するなら2」になることを表します。
なぜこのハミルトニアンで良いのか詳しく知りたい人は$\sigma ^{z}$が位相反転であることを踏まえて以下のMAXCUT問題についてを読むとわかると思います。
http://www.msi.co.jp/nuopt/glossary/term_d3742b6c91ec0451f2d8a7ce8852097519882c55.html
実験
以下が実際に行った実験の手順の概要です。
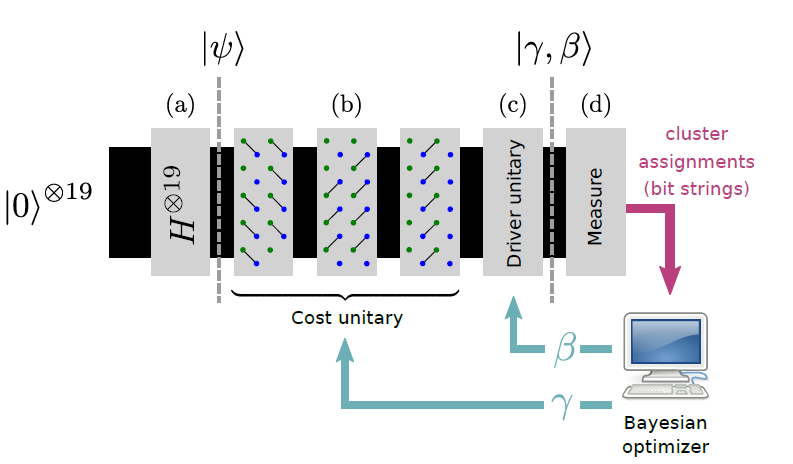
引用:https://arxiv.org/pdf/1712.05771.pdf
ここでCost Unitaryが $ exp(-i \gamma \hat{H} _{cost} ) $、Driver Unitaryが $exp(-i \beta \hat{H} _{ref} )$ のことを言っています。
反復回数pは1で、(γ,β)の最適化にはベイズ最適化を用いています。
また自明なハミルトニアンである$\hat{H} _{ref}$ は$\sigma ^{x}$を用いています。
ここで以下に記載のある$|+>$は、$\sigma ^{x}$の最大のエネルギー固有状態になっています。
手順
① $ |0> ^{\otimes 19} $ にアダマールゲート $H ^{\otimes 19} $ を作用させ$|
\psi > =|+> ^{\otimes 19} $の状態を作成
② $|\gamma , \beta > = exp(-i \beta \hat{H} _{ref})exp(-i \gamma \hat{H} _{cost})|\psi>$ の状態を作成
③ 測定
④ ①~③を複数回行い期待値$ <\gamma , \beta | \hat{H} _{cost} | \gamma , \beta > $ を求める
⑤ 古典PCでベイズ最適化を行い、新しい$(\gamma, \beta)$にして①~④を再度行う
結果
ベイズ最適化を55ステップ、それぞれのステップで量子ゲートにおける測定を2500回測定を行っていました。
これにかかった総時間は約10分間です。
結果のグラフが以下になります。
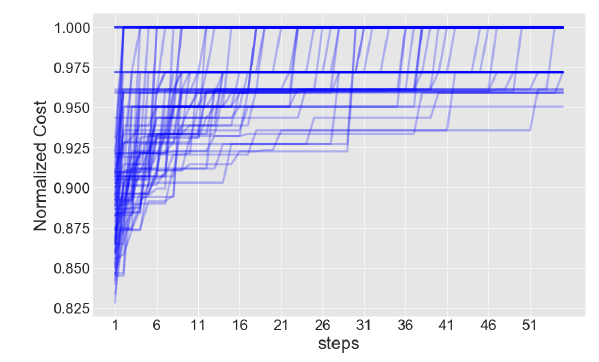
引用:https://arxiv.org/pdf/1712.05771.pdf
縦軸は最適値を1と正規化したときの目的関数値
横軸はベイズ最適化のステップ数です。
グラフより
1回のステップで2500回も測定しているので、どのステップでも最適解が得られているように見られます。
また55ステップよりもっと前からよい近似解が得られるように見られます。
またQAOAと古典PCにおける解を完全にランダムで作成する場合とを比べています。
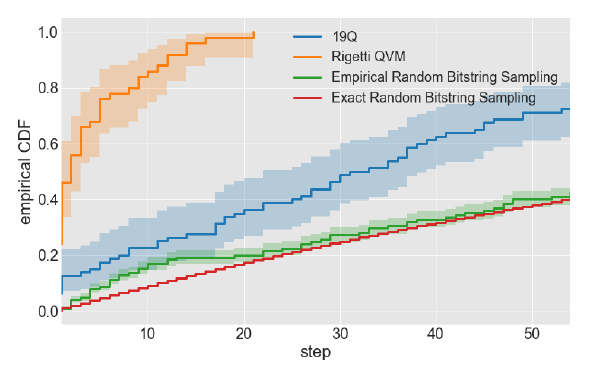
引用:https://arxiv.org/pdf/1712.05771.pdf
Regetti QVMは量子回路を古典コンピュータでシュミレートしたもので、ノイズのない理想的な量子コンピュータのようなものです。
ノイズのない環境だと解の収束がとても速いことがわかりますね。
縦軸は累積分布関数、横軸はベイズ最適化のステップ数になります。
青が今回行ったQAOAで、緑がランダムのベイズ最適化になります。
これより、ランダムよりかは良い結果を早く得られるということがわかります。
考察
ここからは論文を読んで私が考えたことを書こうと思います。
まず思うことが、QAOAの性能を古典アルゴリズムと比較しているところです。
QAOAだけでなく様々な量子アルゴリズムを古典アルゴリズムとを比較するとき、多くの場合がなぜか古典アルゴリズムのランダムに解を作る場合とを比較しています。
これはあまりフェアではないように思っています。最適化やその他の分野でも、問題を解く(古典の)最新のアルゴリズムが研究されています。それらと比較すべきだと思っています。
それらを踏まえて、今回のアルゴリズムの性能を考えてみます。
MAXCUT問題には、Goemans-Williamsonという人たちが作った多項式時間で解ける0.878-近似アルゴリズムが存在します。
しかもこれは、正則グラフではなく任意のグラフで使うことができます。
そうなってくるとQAOAでは、相当数のqubitと繰り返し回数pが無いければ古典PCの性能を超えることが難しいのではないかと思いました。
Goemans-Williamsonのアルゴリズムについて知りたい人は以下を読んでみてください。
http://www-math.mit.edu/~goemans/PAPERS/maxcut-jacm.pdf
http://www.msi.co.jp/nuopt/glossary/term_d3742b6c91ec0451f2d8a7ce8852097519882c55.html
また今回の実験で、計算時間が合計10分間かかっているというところについて考えます。
量子ゲートで状態を作ったり測定を行うといった行為は1回につきナノ秒のオーダー程度になると思います。
そう考えると、このアルゴリズムで一番時間のかかっている部分は古典PCと量子PCとの通信部分が、古典PCでのベイズ最適化の部分ではないかと考えました。
よってQAOAをさらに良くするためには、ベイズ最適化の部分を他の最適化手法でもっと良いものはないのか考えることと、古典PCと量子PCの通信を早くするハードの側面で考えていくのが良いのではないかと考えました。
QAOAは量子断熱計算の考え方がベースになっています。
これは量子アニーリングで使われているものであり、アニーリングを量子ゲートでシュミレートしているのに近いです。
そうならば、最適化問題を解くアルゴリズムについてはアニーリングのほうが未来があるのではないかな、、、とも少し思いました。
関連文献
QAOAは物理的な意味でも面白いものらしく、これの関連論文がいくつか出ています。
A Quantum Approximate Optimization Algorithm Applied to a Bounded Occurrence Constraint Problem
Edward Farhi, Jeffrey Goldstone, Sam Gutmann
https://arxiv.org/abs/1412.6062v2
Quantum Supremacy through the Quantum Approximate Optimization Algorithm
Edward Farhi, Aram W Harrow
https://arxiv.org/abs/1602.07674
Ultrafast State Preparation via the Quantum Approximate Optimization Algorithm with Long Range Interactions
Wen Wei Ho, Cheryne Jonay, Timothy H. Hsieh
https://arxiv.org/abs/1810.04817
まだ読んでないので、まったく中身はわかりませんが近々読みたいと思っています。
コメントなどくれれば自分の分かる範囲でお答えしたいと思っています。
ありがとうございました。