この記事について
量子コンピュータで最適化問題を解くにはアニーリング型では量子アニーリング、ゲート型ではQAOAを利用することになります。
量子アニーリングもQAOAも原理は似ていて時間とともにハミルトニアンを変化させて最終的にコストハミルトニアンの基底状態を求めることを目的としていますが、多少直感的にはわかりづらくなったりするかと思います。
本記事は量子アニーリングやQAOAで
- どのように探索が進むか?
- 一般的に量子力学で語られる話とどのように対応付ければ良いか?
等の観点でなるべく直感的に理解できるように説明していき、理解を手助けすることを目的とします。
まだ勉強段階でかつ、なるべく直感的を目指しているので多少理解が間違っているところもあるかもしれませんが、その際はやさしくコメントをいただけると幸いです。
また、量子コンピュータ関係の他の記事は、下記で紹介しています。
量子アニーリング
わかりやすい記述がないかなと探しているとWikipediaに説明が記載されていたので引用させていただきます。
量子焼きなまし法は、均等な重み付けを持つ全ての可能な状態(候補状態)の量子力学的重ね合わせから開始する。次に、系は物理系の自然な量子力学的発展である時間依存シュレーディンガー方程式に従って変化する。状態間の量子トンネリングを引き起こす横磁場の時間依存強度に応じて、全ての候補状態の振幅は変化し続ける。横磁場の変化速度が十分遅い場合、系は瞬間ハミルトニアンの基底状態の近くにとどまる(断熱量子計算(英語版))[4]。横磁場は最終的に切られ、系は元々の最適化問題の解に対応する古典的イジング模型の基底状態に到達していることが期待される。
とのことです。
これをかなりかいつまんで言うと
- ハミルトニアンは全体として、「初期ハミルトニアン」から「コストハミルトニアン」へ変化し、最終的にコストハミルトニアンの基底状態にとどまることが期待される。
- t = 0 の時点では初期ハミルトニアンの基底状態をとり、真ん中ぐらいでは「真ん中ハミルトニアン」の基底状態をとる。そしてt=Tにおいて「コストハミルトニアン」の基底状態となる。(※真ん中ハミルトニアンという言葉はありません。便宜上つけさせていただきました。)
といったような話になってきます。
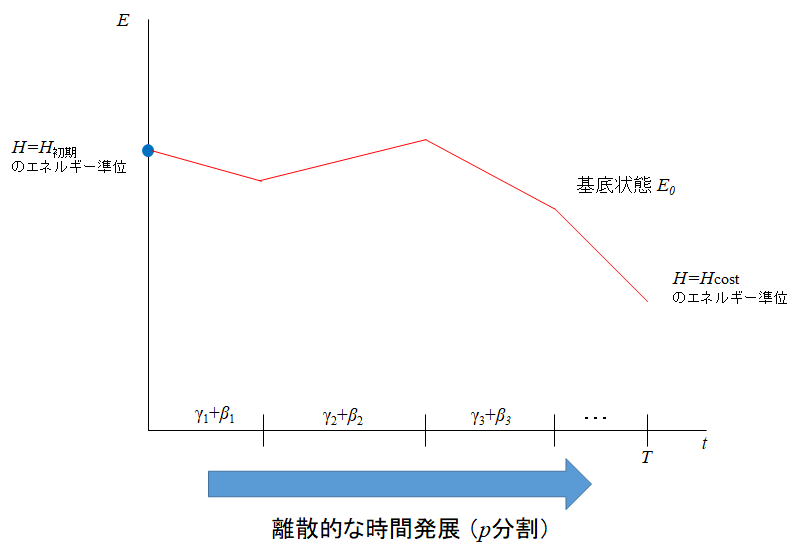
図で示すと以下のようになります。
$t = 0$ の青点で示すものが初期ハミルトニアンの基底状態を示しています。
その状態からハミルトニアンを時間発展させていき、
真ん中あたりでは「真ん中ハミルトニアン」、最終的にコストハミルトニアンの基底状態へとたどり着きます。
つまり、上図の青点から赤線沿いに探索を進めていきます。
注意が必要なのは、上記図からもわかる通り、探索中に基底状態と励起状態が近くなる時間帯が存在します。
その時間帯に最低エネルギー状態から励起状態の一つにジャンプする可能性もあるということです。
そうするとエネルギーが発散する可能性もあります。
詳しくは、こちらを参照すると良いかと思います。
QAOA
ゲート型で最適化を行う際はQAOAを用います。
基本的な考え方は量子アニーリングと似ていることは似ていますが異なる部分も多くあるので整理していきましょう。
QAOAのアルゴリズムの概要は以下となります。
- 重ね合わせ状態$|s\rangle = |+\rangle^{\otimes n}$を作る。
- パラメータ$\beta, \gamma$で指定されるユニタリゲート$U_C(\gamma_{i}),U_X(\beta_{i})$をかけていき、状態$|\beta, \gamma \rangle$を得る。
- 量子コンピュータで期待値 $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ を測定する
- $\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。
- 最適解 $\beta^{ * }$,$\gamma^{ * }$を得るまで1~4を繰り返す。
- $|\beta^{ * } , \gamma^{ * } \rangle$ をZ基底で測定し、良さそうな測定結果を解として出力する。
ここで、$U_C(\gamma), U_X(\beta)$ は次のように定義されます。
U_C(\gamma_{i}) = e^{-i\gamma_{i} C(Z)} = \prod_{\alpha} e^{-i\gamma_{i} C_{\alpha}(Z)}, \\
U_X(\beta_{i}) = e^{-i\beta_{i} \sum_{j=1}^n X_j} = \prod_{j =1}^n e^{-i\beta_{i} X_j}.
シュレディンガー方程式の解を実際に求めに行くと上記のようになり、
これは断熱量子計算で自明な基底状態(簡単な問題に対する基底状態)を持つ初期ハミルトニアンからコストハミルトニアンに時間発展させる $e^{-iHt}$を$p$ステップで変化させるトロッター分解に相当します。
詳しくはこちらを見ていただけると幸いです。
以下のようなユニタリ変換を適用していくことになります。
U(t) = exp(-i \beta _ {p} \hat{H} _{ref} ) exp(-i \gamma _{p} \hat{H} _{cost} ) ・・・・ exp(-i \beta _{1} \hat{H} _{ref}) exp(-i \gamma _{1} \hat{H} _{cost})
$\hat{H}_{cost}, \hat{H}_{ref}$ はそれぞれコストハミルトニアン、初期ハミルトニアンを示します。)
図示してみると以下のようになります。
この図からもわかる通り、$p$は時間発展における分割数、 $\gamma, \beta$はそれぞれの分割の間隔ともとらえられます。(参考)
量子アニーリングと比べると励起状態のグラフがないことが気になります。
ゲート型では励起状態へのジャンプなど考えなくても良いのでしょうか。
と問われると正直私の今の知識では答えられないのでわかる方いたらご教示願いたいです。(またわかればまとめてみようと思います。)
もし、ジャンプがなければ励起状態を気にしなくて良いので少し有効性を高めるポイントなのかなと思っています。
ただし、ゲート型の場合、別途気にしないといけないのは上記のユニタリ変換がトロッター展開による近似であったり、分割の正しさが量子断熱計算における「十分な時間で断熱計算をおこなっているか」といった点に帰着されます。
そのために前述した、
「$\langle \beta, \gamma |C(Z)|\beta, \gamma \rangle$ が小さくなるように古典コンピュータでパラメータ $\beta, \gamma$ を更新する。」
ということを行っていくことになります。
量子力学(無限に深い井戸型ポテンシャル)
※量子力学の専門家ではないのでちょっと調べて出てきた程度の知識で述べてしまい多少間違いがあるかもしれませんが、温かい目で見守ってください。(できればコメントください。)
量子力学の初歩で扱う例題として無限に深い井戸型ポテンシャルの話があります。
詳しくはこちらの動画をみていただけると良いかと思います。(よびのり先生わかりやすくて良いです。)
結論だけ記述すると
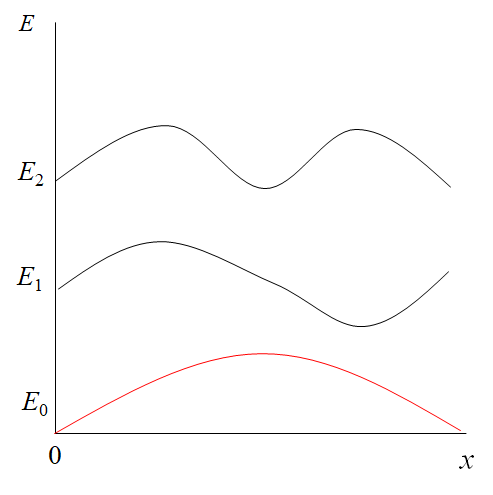
無限に深い井戸型ポテンシャルでは以下の通り粒子のエネルギー準位が図示されることが多いです。
注意したいのはこちらの横軸が $x$となっていることです。
つまり、横軸に位置をとっています。
もちろん今回は無限に深い井戸型ポテンシャルの例題を例に挙げたからではありますが、このような問題では一般的に時間を固定して位置を変数として解を求めに行くことが多いようです。
(そうでなければ申し訳ありません。少なくとも私はそう思っていました。)
そのため、この図を用いて時間発展で考える量子断熱計算を理解しようとすると無理があります。
量子断熱計算の場合は横軸に時間をとるためそのまま対応付けると良く分からなくなります。
というわけで最後に量子の世界とコンピュータの世界の対応付けを行ってから終わろうと思います。
時間と位置の対応
量子アニーリングとQAOAを別々に考えてもあまり変わらないので
今回は量子アニーリングの場合のみ考えてみます。
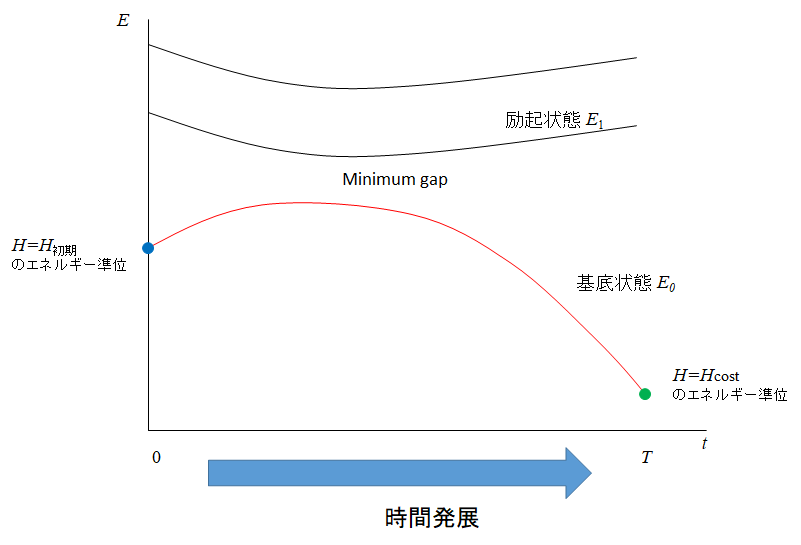
前述した量子アニーリングの図をもう一度示します。
最適な状態でアニーリングを進めることができた場合、量子状態は常に基底状態を維持して最後の緑点にたどり着きます。
つまり、任意の位置に対するエネルギー状態ということです。
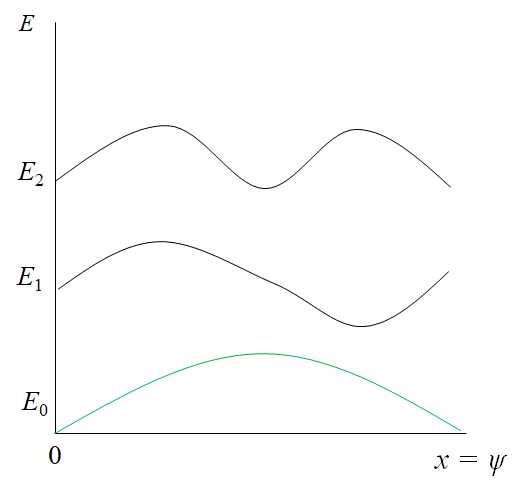
では位置を横軸にとってみると以下のようになります。
上記の緑線が一つ前の図の緑点と対応づいています。
また、横軸が位置ということなので結局のところ任意の量子状態を示すことになります。
(※上記はきれいなsin関数cos関数になっていますが、実際の最適化問題ではこのようにきれいな関数とはなりません。)
ということで横軸に時間の量子断熱計算を横軸に位置で表すことができました。
最後に
実は本記事を書くきっかけは自分が混乱していたということがあります。
井戸型ポテンシャルではこう書いてあるけど、量子アニーリングとQAOAの説明ではなんか違うぞ!といった違和感からちゃんと考えてみました。
正直に言いますと横軸をちゃんと確認しておけば良いのでは?という感じではありますが、それを含めていろいろと勉強になりました。
何かのお役に立てればと思います。