ゼロから作る自動ダメージ最大化シミュレーター
この記事では自動ダメージ最大化シミュレーターを作る方法をゼロから解説していきます。
この記事を読むと、ゲーム中でダメージが最大になる装備構成を自動で見つけてくれるシミュレーターを実装することができます。シミュの動作イメージを知りたい方は以下のサイトを開いて右下の 最適化ボタン を押してみてください。
こちらのサイトは弓専用の自動ダメージ最大化シミュレーターですが、本記事を読むと弓に限らず別武器のシミュも実装できますし、より馴染みのあるスキルシミュレーターも実装可能です。記事の途中でスキルシミュも実装します。
結論の実装を先に読みたい方は以下のリポジトリの dmax.py というファイルを参照してください。この500行程度のコードがシミュの核心部分です。
github/dmax-from-scratch-sample-code
コード自体はシンプルですが、ハイコンテクストなのでわかりづらいと思います。本記事の読了後にはこちらのコードを理解し、改変できるようになります。
本記事は少し長いですが、1つの記事で全文とソースコードを掲載しており折りたたみもありません。したがって、ソースコードのわからない部分を検索して辞書のように利用することも可能です。
文章の構成はシミュレーターの解説→実装という順序になっています。
具体例とポンチ絵を駆使してできるだけ詳しく、発想から説明するように心がけます。
サンプルコードをベースに読者が別武器や次回作のシミュを実装できるような記事を目指します。
自動ダメージ最大化シミュレーターとはなにか?
自動ダメージ最大化シミュレーターは、ゲーム中でダメージが最大になる構成を自動で見つけてくれるシミュレーターです。
モンスターハンターというゲームには数千件の装備があり、装備の組み合わせが変わるとモンスターに与えるダメージが変化します。この与ダメージが最大になる装備の組み合わせを自動で考えてくれるのが自動ダメージ最大化シミュレーターです。
自動ダメージ最大化シミュレーターでは長いので以降は最適化シミュと表記します。
💡 スキルシミュとダメシミュを融合するイメージ
より強い装備を実現したい場合、通常はスキルシミュレーターとダメージシミュレーターを交互に利用して、実現可能な範囲できるだけ高いダメージを出せる装備を探すというアプローチを取ります。自動ダメージ最大化シミュレーターでは、この 「スキルシミュとダメシミュを利用して最大ダメージ構成を見つける」という処理を自動で実行し、かつ、それが最大ダメージ構成であることを保証してくれます。
最適化シミュの仕組み
自動ダメージ最大化シミュレーターの仕組みを一言で言うと、「最適化ソルバーに解かせよう!」です。
世の中には最適化ソルバーという素晴らしいツールがあり、これがモンハンの最大ダメージ構成を考える上でのさまざまな難しい問題をまとめて解決してくれます。最適化ソルバーの内部の仕組みは難しいですが、利用するだけであればそれほど難しくはありません。
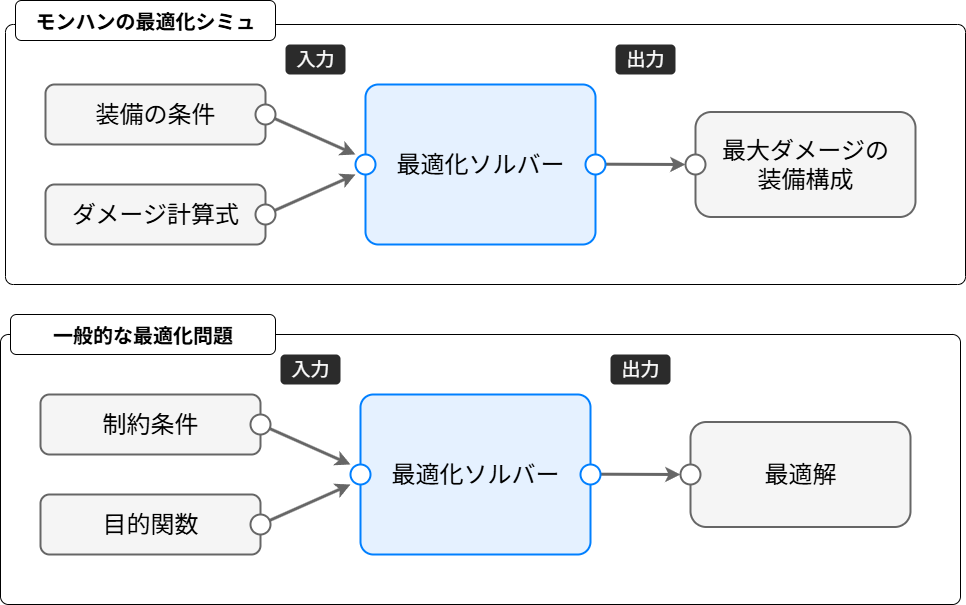
最適化ソルバーには以下のような嬉しい性質があります。
最適化ソルバーに対して「
装備の条件とダメージ計算式」を入力すると、「ダメージが最大になる装備の組み合わせ」が出力される
より一般的に言うと以下のような性質があります。
最適化ソルバーに対して「
制約条件と目的関数」を入力すると、「その制約条件の範囲内で、目的関数が最大 or 最小になるような解」が出力される
モンハンの場合、「制約条件」が「装備の条件」に相当し、「目的関数」が「ダメージ計算式」に相当します。
ここで言う「装備の条件」とは、例えば「頭防具は1つしか装備できない」とか「装飾品はスロットが合うものしか装備できない」のような条件です。ゲームをプレイする上で暗黙のうちに了解しているさまざまな装備の制約を入力する必要があります。
また、ここで言う「ダメージ計算式」とは「攻撃力〇〇の弓を装備して△△モーションをモンスターに当てると✕✕のダメージになる」のようなダメージを決定する計算式のことです。
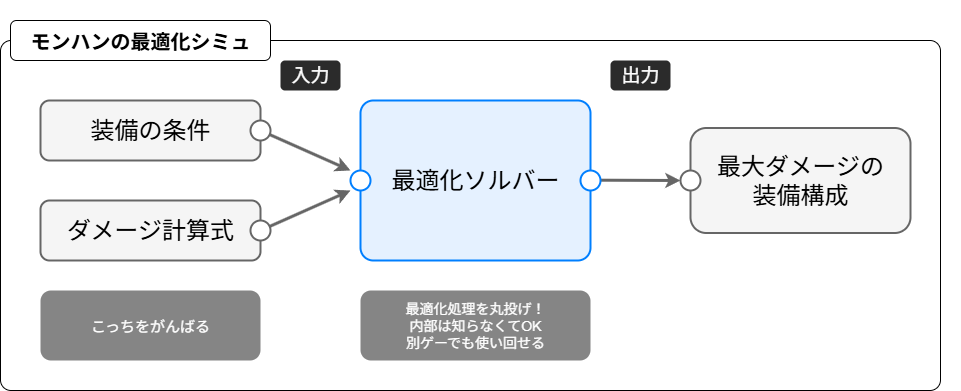
最適化ソルバーは、ソルバー内部の最適化処理の仕組みを知らなくても利用できます。ソルバーの内部はブラックボックスのまま扱えるということです。そのため、それぞれのゲームの条件を考慮して最適化処理を自分で実装する必要がなくなります。この記事で作っていく最適化シミュ は「難しい部分は最適化ソルバーに丸投げ!」というアプローチで、最大ダメージ装備を探します。
ただし、最適化ソルバーは一定のフォーマットで入力しなければ最適化問題を解くことができません。そのため、最適化シミュを実装するうえでのチャレンジは「装備の条件とダメージ計算式をどのようにして最適化ソルバーが解ける形式に落とし込むか?」という点になります。「装備の条件」と「ダメージ計算式」を最適化ソルバーが理解できる形式で入力することができれば、最適化シミュは完成です。
ダメージ計算式については、すでに計算式がわかっているのであれば最適化ソルバーに入力するのは難しくありません。計算式をそのまま記述するだけです。(ダメージ計算式において難しいのは、どのようにしてダメージ計算式を推測するか?という点です)
したがって問題は、「装備の条件をいかに最適化ソルバーが解ける形式に落とし込むか」になります。以降ではこの方法を見ていきます。
装備の条件を数式に落とし込む
ここまでの説明で、モンハンの装備条件を最適化ソルバーが解ける形式に落とし込む必要があることを見てきました。
最適化ソルバーが解ける形式とは数式のことです。つまり、装備条件を数式として表現することができれば良いことになります。
実際のゲームデータを利用すると複雑になってしまうため、最初はサンプルデータを用意して説明していきます。(この記事の後半では、実際のゲームデータを利用して最適化シミュを実装していきます。)
武器A: 攻撃力 20
武器B: 攻撃力 10
ゲーム内の暗黙の条件: 武器は1つしか利用できない
ダメージ計算式: (ダメージ) = (武器の攻撃力)
非常にシンプルなサンプルデータを用意してみました。
ダメージ計算式は武器の攻撃力をそのまま参照するため、攻撃力が高い武器Aのほうが高い与ダメージを得ることができます。つまり、この場合の最大ダメージ構成は「武器Aを1つ装備する」になります。
ここまでシンプルであれば、もはや最適化ソルバーなどという大袈裟なものを持ち出すまでもなく、直感的に最も強い構成がわかると思います。しかし、ここでは装備条件を制約式の落とし込む練習のため、あえてこの問題を最適化ソルバーが解ける形式で表現してみましょう。
重要な条件として、武器は1つしか利用できないという条件があるので、これを制約式として表現してみます。
まずダメージ計算式は以下のようになります。
(ダメージ) = (武器Aの攻撃力) * (武器Aを利用する) + (武器Bの攻撃力) * (武器Bを利用する)
これを数式っぽく表現すると以下のようになります。
dmg = A_attack * A_use + B_attack * B_use
A_attack は武器Aの攻撃力 20 であり、変化しません。
B_attack は武器Bの攻撃力 10 であり、変化しません。
つまりダメージ計算式は以下のように書けます。
dmg = 20 * A_use + 10 * B_use
A_use は武器Aを利用するかどうかを表す変数であり、0 または 1 のどちらかの値を取ります。
B_use は武器Bを利用するかどうかを表す変数であり、0 または 1 のどちらかの値を取ります。
「武器は1つしか利用できない」という条件があるので、 A_use + B_use は2以上になることはありません。つまり、A_use + B_use は1以下という制約条件が必要になります。
A_use + B_use <= 1
最終的に、以下のような装備の制約条件と目的関数が導かれました。あとは、こちらを最適化ソルバーに入力すると、最大化問題の解として (A_use, B_use) = (1, 0) の組み合わせが出力され、「武器Aを使用したほうが与ダメージが高い」ということがわかります。
制約条件:
A_use + B_use <= 1
0 <= A_use <= 1 (ただし A_use は整数)
0 <= B_use <= 1 (ただし B_use は整数)
目的関数:
20 * A_use + 10 * B_use
ここまでの流れを見ると、「直感的にわかることを複雑に書いてる」と感じるかと思います。しかし、このような条件を数式に落とし込む手順を発展させていくと、問題が複雑になり人力ではとても解けないような規模の問題になった場合でも最適化ソルバーを利用して問題を解けるようになるので、いましばらくお付き合いください。
さて、上記の問題については完成した「制約条件と目的関数」を最適化ソルバーに投げて終了なのですが、最適化ソルバーの性質について理解を深めるためもう少し深堀りしましょう。
上記の制約条件と目的関数をグラフで表現してみましょう。
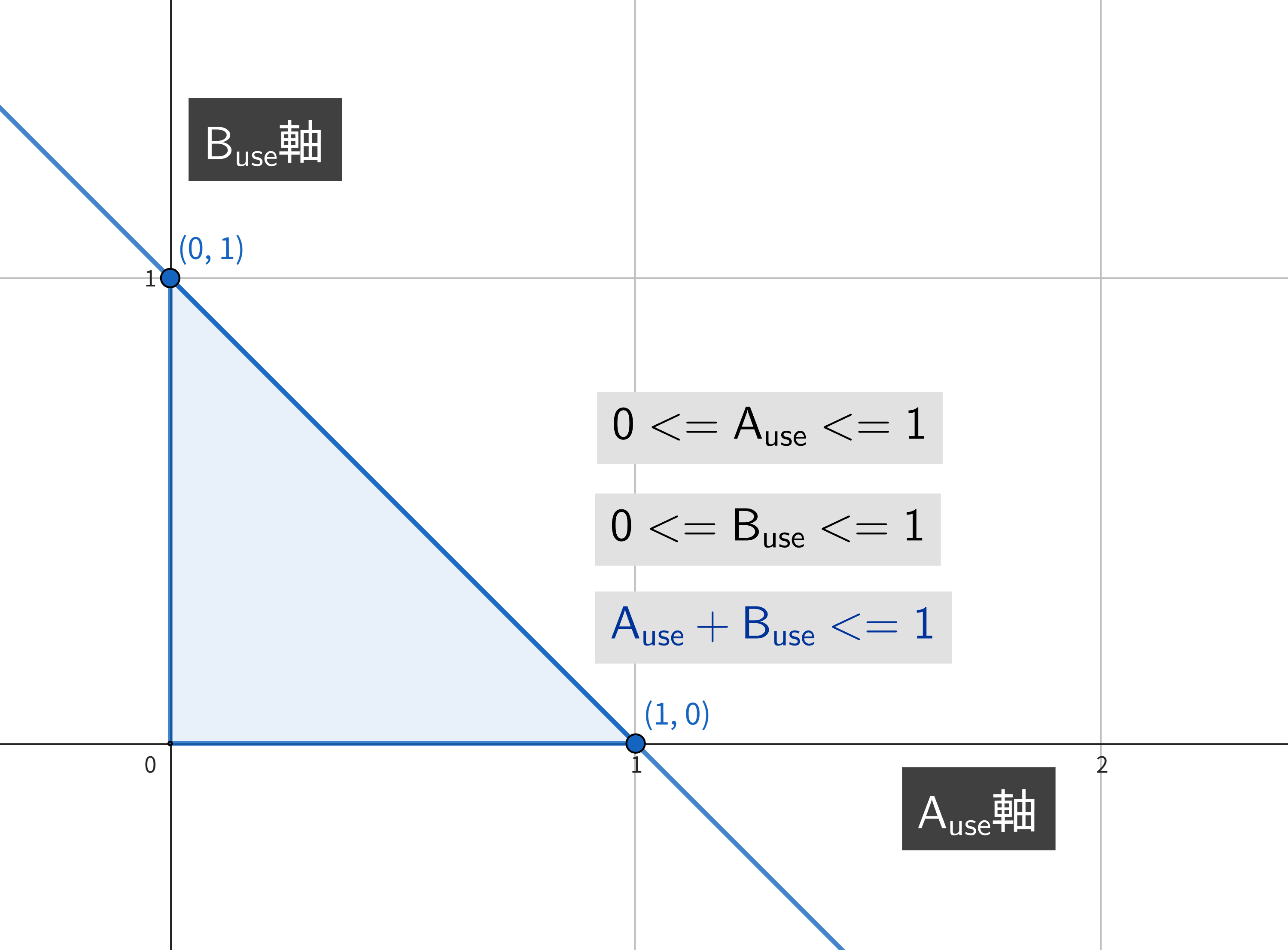
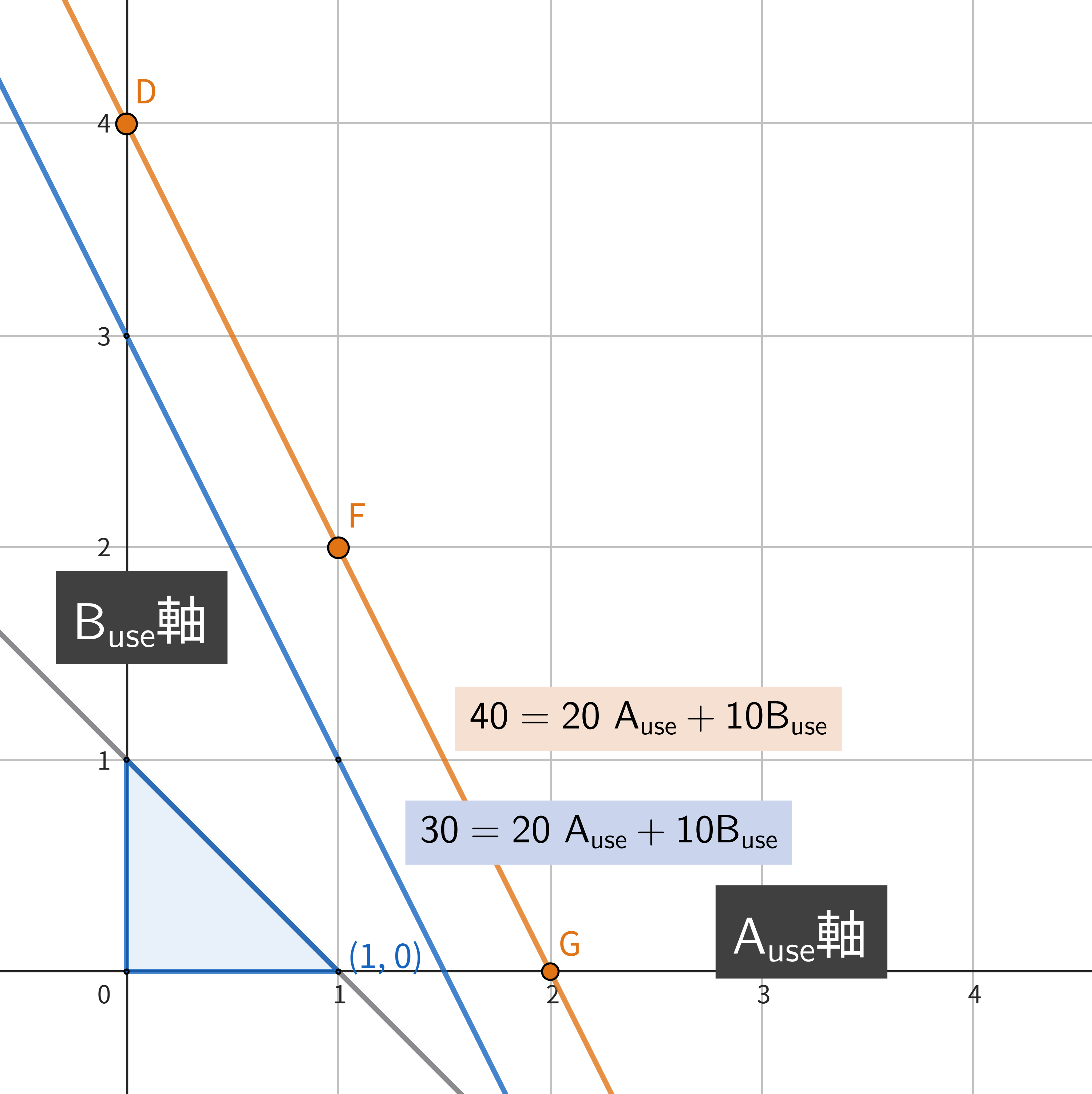
まず以下の制約条件をグラフ上に図示します。
横軸が A_use の値を表し、縦軸が B_use の値を表しており、制約式の範囲は図のような正方形の領域の頂点になります。
0 <= A_use <= 1 (ただし A_use は整数)
0 <= B_use <= 1 (ただし B_use は整数)
ここで、さらに以下の制約式を追加すると、制約式の範囲は図のような三角形の領域になります。
A_use + B_use <= 1
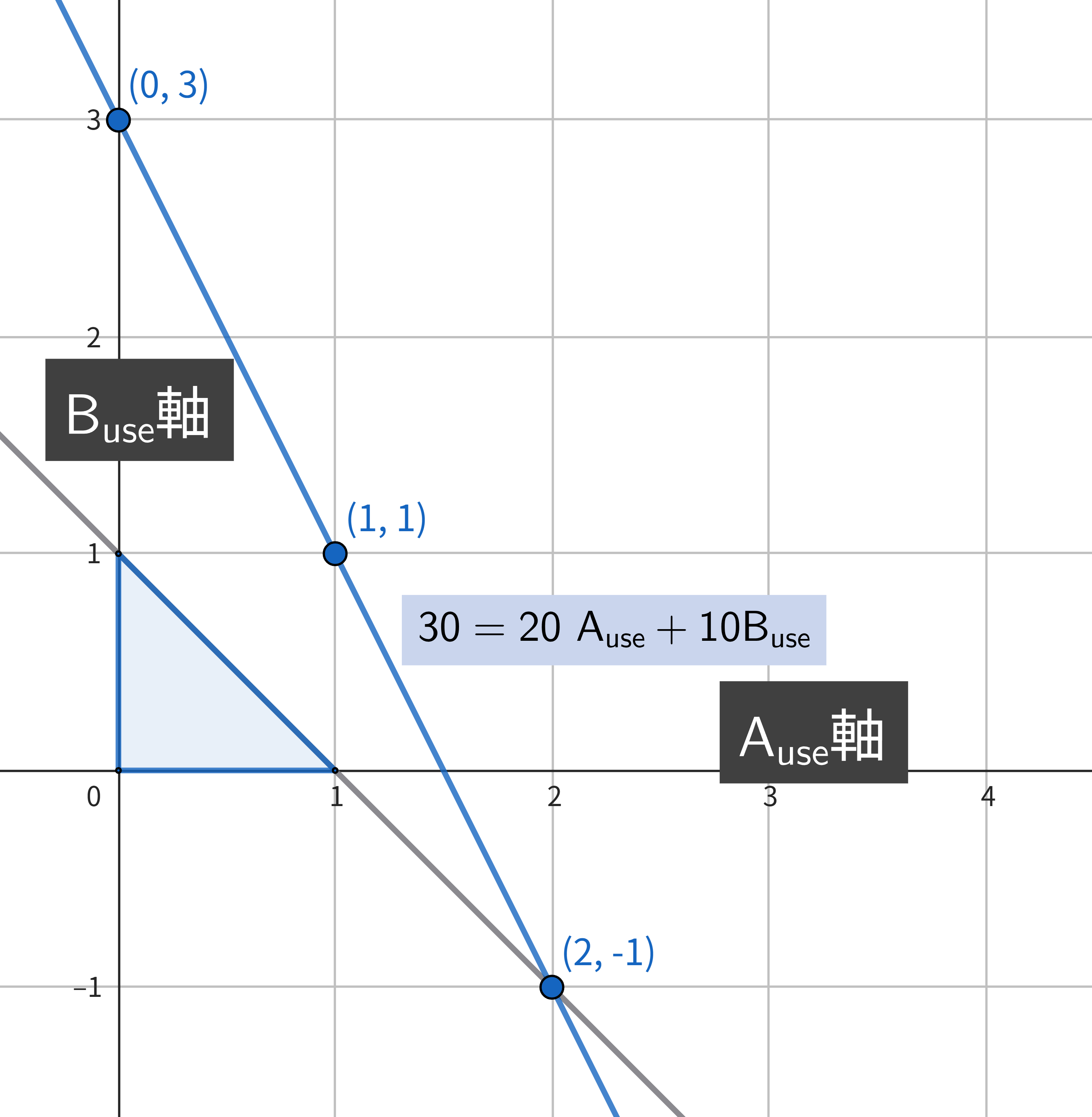
最後に目的関数 20 * A_use + 10 * B_use はグラフ上でどのように表現できるかを考えます。
まず、 20 * A_use + 10 * B_use = 30 になる点をリストアップしてみると、(A_use, B_use ) = (0, 3), (1, 1), (2, -1) となります。これを線でつなぐと、 20 * A_use + 10 * B_use = 30 を満たす線を引くことができます。この線は、同じ30という値を取る線なので等高線と呼べます。
次に 20 * A_use + 10 * B_use = 40 となる等高線を引くと以下のようになります。
つまり、20 * A_use + 10 * B_use の等高線は 20 * A_use + 10 * B_use = 30 の等高線に対して並行な直線になります。
ここで、 20 * A_use + 10 * B_use はダメージ計算式なので、大きければ大きいほどプレイヤーにとって嬉しいです。なので、等高線をできるだけ右上にズラしていきたいです。しかし、A_use と B_use には制約条件があり、グラフ上で図示された点しか取ることができません。よって、A_use と B_use のグラフ上の点のうち、最も等高線が右上になる値の組み合わせ (A_use, B_use) = (1, 0) が、ダメージ計算式を最大化する最適解ということになります。
また、20 * A_use + 10 * B_use = 20 より最適解によって得られる最大ダメージは 20 であることも分かります。
つまり、ダメージ計算式の等高線を引き、等高線が高い方から低い方へ動かしていき、制約条件の表す範囲に重なる等高線まで動かして止めれば最大化問題が解けたことになります。
最適化ソルバーは、内部的にこのようなアプローチで最適化問題を解いています。実際にはもっと別の高度な仕組みで解いていますが、最適化シミュを実装するうえでは大雑把なアプローチを理解しておけば十分です。
装備の条件を数式に落とし込む 応用編
次は、問題設定をもう少しモンハンの装備条件に近づけてみましょう。(この装備条件は後のセクションにおいてプログラムで実装し、最適化ソルバーに解かせます。)
武器C: 攻撃力 30, 属性値 20
防具X: 攻撃強化Ⅱ, 属性強化Ⅰ, 体術 x2, 重量1kg
防具Y: 攻撃強化Ⅰ, 属性強化Ⅱ, 体術, 重量2kg
スキルの効果:
攻撃強化Ⅰ: 攻撃力を +10 (装備全体で「攻撃強化Ⅰ」がN個ついている場合、攻撃力の加算値は +10*N とする。攻撃強化Ⅱ,属性強化Ⅰ,Ⅱについても同様)
攻撃強化Ⅱ: 攻撃力を +30
属性強化Ⅰ: 属性値を +20
属性強化Ⅱ: 属性値を +30
体術: ダメージ計算には寄与しない
装備の条件:
(条件1) 防具は0個以上のいくつでも装備できる
(条件2) 体術は最低5個欲しい
(条件3) 防具重量の合計の上限は4kg (4kg 以上の防具は重くて装備できない)
ダメージ計算式:
(ダメージ) = {(武器の攻撃力) + (攻撃強化スキルによる攻撃力加算)}
+ {(武器の属性値) + (属性強化スキルによる属性値加算)}
(モンハンには重量制限はなく装備を無限に装備することもできませんが、ここでは条件を式に落とし込む練習のために都合の良い条件を設定しています。)
さて、こうなると直感で解くのは難しくなってきたのではないでしょうか?
まずは、先ほどと同じように上記の条件を制約式として表現し、グラフという簡易的な最適化ソルバーで解いてみましょう。
防具Xを装備する数を X_use, 防具Yを装備する数を Y_use とします。
まず (条件1) を考えます。
(条件1) 防具は0個以上のいくつでも装備できる
という制約条件を数式で表すと以下のようになります。
0 <= X_use (ただし X_use は整数)
0 <= Y_use (ただし Y_use は整数)
次に (条件2) を考えます。
(条件2) 体術は最低5個欲しい
防具Xには体術が2個付いているので、防具Xを X_use 個装備したときの体術の合計は 2 * X_use 個になります。
よって (条件2) を数式で表すと以下のようになります。
2 * X_use + 1 * Y_use >= 5
同様に考えて、 (条件3)
(条件3) 防具重量の合計の上限は4kg
を数式で表すと以下のようになります。
1 * X_use + 2 * Y_use <= 4
次に、以下のダメージ計算式を考えます。
ダメージ計算式:
(ダメージ) = {(武器の攻撃力) + (攻撃強化スキルによる攻撃力加算)}
+ {(武器の属性値) + (属性強化スキルによる属性値加算)}
スキルの効果:
攻撃強化Ⅰ: 攻撃力を +10
攻撃強化Ⅱ: 攻撃力を +30
属性強化Ⅰ: 属性値を +20
属性強化Ⅱ: 属性値を +30
各スキルの効果を考慮すると、ダメージ計算式は変数 X_use, Y_use を利用して以下のように書き直せます。
(ダメージ) = {(武器の攻撃力) + 10 * (攻撃強化Ⅰの個数) + 30 * (攻撃強化Ⅱの個数)}
+ {(武器の属性値) + 20 * (属性強化Ⅰの個数) + 30 * (属性強化Ⅱの個数)}
防具Xには攻撃強化Ⅱがついているので、X_use 個装備すると 30 * X_use の攻撃力が加算されます。
防具Yについても同様に考えるとダメージ計算式は以下のように表現できます。
dmg = {(30) + 10 * Y_use + 30 * X_use}
+ {(20) + 20 * X_use + 30 * Y_use}
= 50 + 50 * X_use + 40 * Y_use
ここまでで制約条件と目的関数を変数 X_use, Y_use を利用して表現できました。
制約条件と目的関数をまとめると以下のようになりました。
制約条件:
0 <= X_use (ただし X_use は整数)
0 <= Y_use (ただし Y_use は整数)
2 * X_use + 1 * Y_use >= 5
1 * X_use + 2 * Y_use <= 4
目的関数:
50 + 50 * X_use + 40 * Y_use
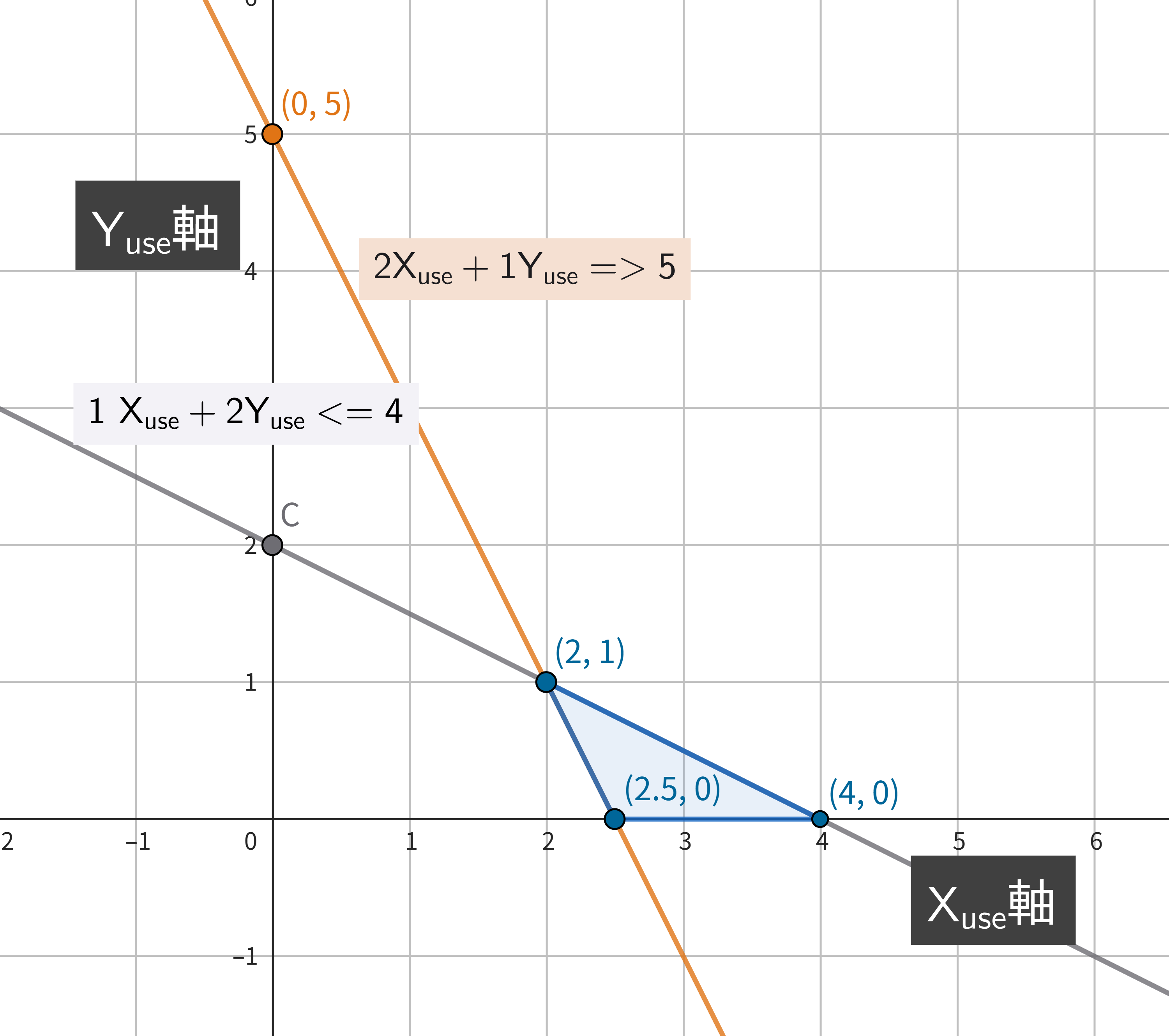
それでは次にグラフに図示し、最適解を求めてみましょう。
まず、制約条件をグラフに図示すると以下のようになります。青い三角形の領域が制約条件を満たす解の範囲です。さらに、整数の制約も考慮すると解の候補は (X_use, Y_use) = (2,1), (4,0) のいずれかに絞れます。
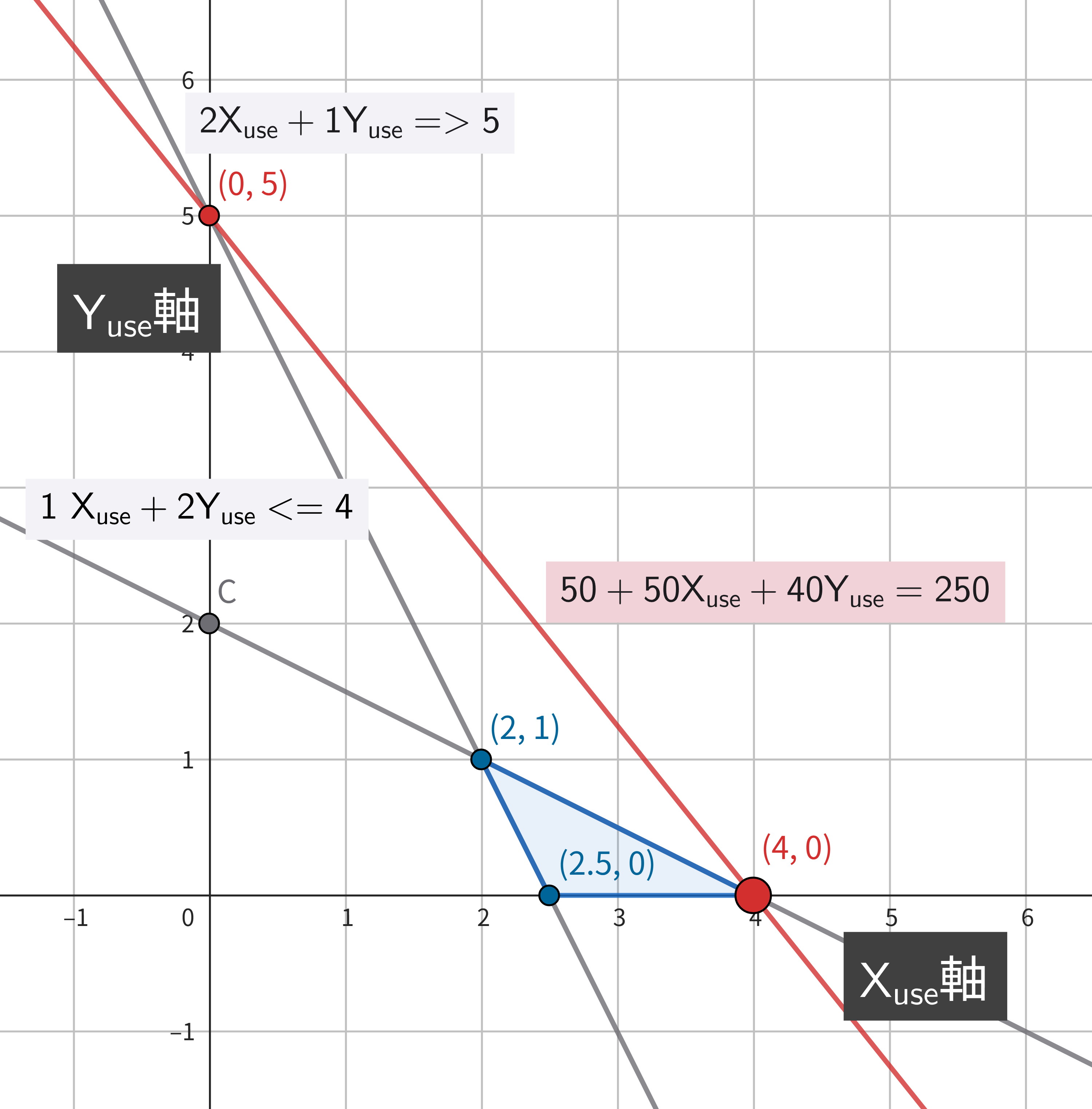
次に先ほどと同様に目的関数の等高線を考慮すると、50 + 50 * X_use + 40 * Y_use = 250 の場合に制約条件を満たし、かつ目的関数が最大となることがわかります。
よって、制約条件を満たす解のうち最大ダメージを実現する解は (4,0) であり、その最大ダメージは 250 であることがわかりました。
このセクションでは、問題を制約条件と目的関数に落とし込み、さらに作図により最適解を求めました。後のセクションでは、この問題をプログラムとして表現し、最適化ソルバーに解かせるところまで実施します。
実際の最適化シミュを実装するうえでは、「作図により最適解を求める」部分は最適化ソルバーの仕事になるため、この部分は不要になります。しかし、作図部分の動作原理は最適化ソルバーの最も簡単な動作を模倣したものなので、どのような問題であれば最適化ソルバーが高速に解けるのかについての示唆を得ることができます。
ここで登場した制約条件や目的関数は説明のために簡単な例を出しました。ここでいう簡単とはどういう意味かというと、制約条件や目的関数の中に変数同士の掛け算がない形式になっています。変数同士の積がない or 少ないことは人間にとっても解きやすく、また最適化ソルバーにとっても高速に解けるものになります。利用する最適化ソルバーによっては変数同士の積があると問題を解くことができません。
どうやって式に落とし込めばよいか?
前のセクションではゲームの条件としてシンプルな例を題材に考えたので、定式化がスムーズにできました。しかし、モンハンのような実際のゲームは複雑であり、定式化が難しくなります。このセクションでは複雑な問題に対する定式化の方針について見ていきます。
最適化問題の定式化の方針がわからない場合は以下の問いを立ててください。
(1) この問題における最適解とはなにか?
(2) この問題における解の候補とはなにか?
(3) この問題における変化する値はなにか? (変数はなにか)
(4) この問題における変化しない値は何か? (定数はなにか)
上記の4点が整理できれば最適化問題として式に落とし込めます。
まず (1), (2) について、先程の具体例で整理してみます。
(1) この問題における最適解とはなにか?
(2) この問題における解の候補とはなにか?
先程の例における最適解は (X_use, Y_use) = (4, 0) という組み合わせでした。また、解の候補としては X_use と Y_use の任意の組み合わせが考えられます。例えば (X_use, Y_use) = (4, 0), (0, 0), (0, 5) などです。
つまり、最適解とは、「無数に存在する解の候補 (X_use, Y_use) の組み合わせのうち、全ての制約条件を満たしかつ、目的関数が最大となる解である」と表現できます。解の候補は変化する値なので変数として表現できます。
次に、 (3), (4) についても同様に具体例で整理してみます。
(3) この問題における変化する値はなにか? (変数はなにか)
(4) この問題における変化しない値は何か? (定数はなにか)
先程の例で登場した「(条件2) 体術は最低5個欲しい」を考える場合、(X_use, Y_use) の組み合わせは解候補であり、最適解を探す上で変化する値、すなわち変数です。
逆に、「防具Xには体術が2個付いている」というデータから導き出される 2 という値は、最適解を探す上で変化しない値、すなわち定数です。同様に、「防具Yには体術が1個付いている」というデータから導き出される 1 という値も定数です。さらに、「(条件2) 体術は最低5個欲しい」という条件にも下限が 5 であるという定数値があります。
以上のように考えて抽出した変数 X_use, Y_use と定数 2, 1, 5 を利用すると、「(条件2) 体術は最低5個欲しい」は以下のように式に落とし込めます。
2 * X_use + 1 * Y_use >= 5
制約条件式を立式する際には以下のルールを満たせば、最適解を得ることができます。
(1) 変数と定数からなる式によって制約条件式と目的関数を表現すること
(2) 全ての制約条件を満たす最適解が存在すること
シミュ高速化のコツ
最適化ソルバーの性質として 変数同士の掛け算が少ないほど問題を高速に解ける という性質があります。
例えば、変数 x と変数 y がある場合、
- $3xy$ という式よりも、 $3x + 2y$ のような式のほうが高速に解ける
- $3x^2 + 2xy$ という式よりも、 $3x + 3x + 2x + y$ のような式のほうが高速に解ける
ということです。変数の数自体はどちらも同じですが、後者のほうが変数同士の掛け算が少なく、より高速に解くことができます。
変数同士の掛け算を減らした究極系、つまり変数同士の積がない式は一次式と呼ばれています。またこのような式の性質は線形性と呼ばれることがあります。(厳密には数学的な線形性ではありませんが、工学などの応用系の分野では一次式を雑に「線形である」と呼ぶことがあります。)
つまりもし、モンハンのダメージ最大化問題の制約条件とダメージ計算式を、この一次式の形に落とし込むことができたなら、より高速なシミュが作れるかもしれないということです!ただし、変数同士の積を減らすために補助変数を導入すると、補助変数と制約式が増えるため必ずしも高速化するとは限らない点には注意が必要です。(DMAX MHWilds の実装には変数同士の積があるので、この点において改善の余地があるかもしれません)
とはいえ、立式する際の方向性として「変数同士の積を減らす」という意識を持っておくことは重要です。実際のモンハンのゲーム内条件を式に落とし込む際に、変数同士の掛け算を減らせないか?という視点を意識すると、より高速な最適化シミュを作れる可能性が上がります。逆に、変数同士の掛け算が多すぎると計算が重くなってしまい、実用に耐えないほど遅い最適化シミュになってしまう可能性が高くなります。
💡 サンブレイクはワイルズより重い
実際の例として、サンブレイクの最適化シミュ は ワイルズの最適化シミュ よりも最適解が見つかるのに時間がかかります。
サンブレイクもワイルズも仕組み的には同じ実装をしており、どちらも同じ最適化ソルバーを利用しています。しかしサンブレイクのほうが攻撃力と属性値に対して乗算で効果があるスキルが多いため、変数同士の掛け算が多くなり結果として処理が重くなっています。また装備のデータ数が多い点もサンブレイクのほうが処理が重い原因の1つです。
変数同士の掛け算があってもOK
高校数学で登場する線形計画法に慣れていると「最適化ソルバーは線形でない問題は解けない」という思い込みがあるかもしれません。(私も以前は漠然とそう思っていました)
実際に、問題が線形でないと解けないソルバー (線形計画ソルバー) もありますが、問題が線形になっていなくても (非線形であっても) 解けるソルバーもあります。
本記事の最適化シミュではSCIPという最適化ソルバーを利用します。SCIPソルバーは無料で利用できるソルバーでありながら、非線形の最適化問題を解けます (Apache 2.0 License)。 より正確にいうと SCIP ソルバーは MINLP という形式の問題を解くことができます。MINLP (Mixed Integer Nonlinear Programming) は混合整数非線形計画問題のことで、制約条件式や目的関数が非線形であっても解くことができますし、一部の変数に整数の制約があっても (つまり混合整数問題であっても) 解くことができるという優れものです。
なので、式に落とし込む際に変数同士の掛け算ができてしまっても、それを解けるソルバーはあるので諦めず実装してみましょう。
(ただし、問題の規模によっては実用に耐えないほど遅くなる可能性はあります)
最適化問題の実装
ここまでの説明で、モンハンに模した装備条件やダメージ計算式を、最適化ソルバーが解ける形式に落とし込む方法を見てきました。
前のセクションではグラフを利用して解きましたが、次は実際にプログラムを書いて最適化ソルバーに解かせてみましょう。
最適化問題の設定としては、先程の制約条件と目的関数をそのまま利用します。
制約条件:
0 <= X_use (ただし X_use は整数)
0 <= Y_use (ただし Y_use は整数)
2 * X_use + 1 * Y_use >= 5
1 * X_use + 2 * Y_use <= 4
目的関数:
50 + 50 * X_use + 40 * Y_use
ここから、制約条件と目的関数をプログラムで表現していきます。
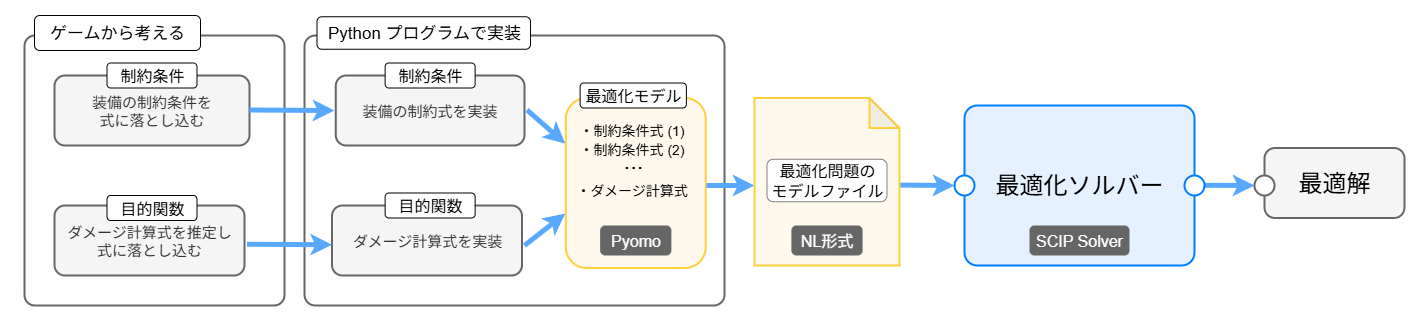
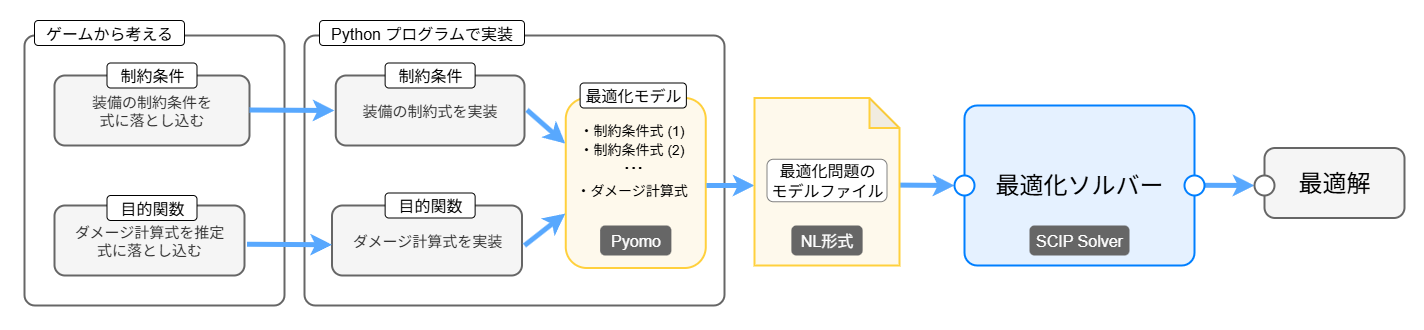
最適解を得るまでの処理の流れは以下のようになります。
- ゲームをベースに装備の制約条件を整理し、ダメージ計算式を推定します
- Python プログラムにより制約条件とダメージ計算式を実装し、最適化問題のモデルに追加します
- 最適化問題のモデルをファイルに出力します
- モデルファイルを最適化ソルバーに入力し、最適解の出力を得ます
Python プログラムでは最適化問題をモデルとして定義します。モデルに対して制約条件や目的関数、変数やパラメータなどを追加していくイメージです。
モデルを定義するためには Pyomo というモデリングツールのライブラリを利用します。
定義された最適化問題のモデルはファイルに出力することができます。ファイルの形式としては非線形問題を扱える AMPL NL形式 (Nonlinear) を利用します。出力されたモデルファイルを最適化ソルバーに入力すると最適化を実行できます。
最適化ソルバーとしては SCIP を利用します。
Python, Pyomo, SCIP はいずれもそれぞれのライセンスのもと無料で利用できます。
環境構築(0): 環境の全体像
まずは、プログラミングをはじめる際の最大の難関、環境構築をやっていきましょう。
SCIPソルバーはC/C++によって実装されたネイティブバイナリを実行する形式のプログラムなので、Python や Java のようなランタイムが面倒を見てくれる環境に比べて環境構築の難易度は高めになります。気合を入れてやっていきましょう。
環境は以下になります。
| 必須 | 項目 | 内容 |
|---|---|---|
| OS | Ubuntu 22.04.1 LTS | |
| Python インタプリタとライブラリのバージョン管理 | uv | |
| ✅ | Python 実行環境 | Python 3.8.16 |
| ✅ | モデリングツールのライブラリ | Pyomo 6.4.4 |
| ✅ | 最適化ソルバー | SCIP version 8.0.3 |
OS を Ubuntu 22.04.1 LTS としているのは主に最適化ソルバー SCIP の実行環境のためです。
SCIP はC/C++で実装されており、ネイティブバイナリ形式のファイルを実行する形になるため、OSを揃えておいたほうがトラブルは少ないと思います。
一応 SCIP のパッケージとしては Linux/Windows/MacOS/Raspberry の環境のコンパイル済みパッケージが提供されているのでどの環境でも動かせると思いますが、この記事では試していません。
Python や Pyomo ライブラリは基本的にどのOSでも問題なく動くと思います。
ただしできればバージョンは揃えておきたいです。個人的に Python 環境はバージョンがズレるとすぐに動かなくなるイメージがあります。実際にはそこまで簡単に動かなくなるわけではないですが、揃えられるなら Python やライブラリのバージョンを揃えておくに越したことはありません。
というわけでバージョン管理ツール uv の利用を推奨します。uv を利用すると uv sync というコマンド一発で仮想環境を構築し、 Python インタプリタと Pyomo 等のライブラリのバージョンを揃えることができます。
この記事では Windows11 の WSL2 環境で実行環境を構築していきます。
その他のOSの方は、本記事の手順を参考に上記の表の必須の項目を準備してください。(ChatGPT, Gemini, Claude などに聞けば教えてくれると思います。)
環境構築(1): WSL2 の有効化
- 既にWSL2のUbuntu22.04環境がある方はスキップして、
環境構築(3): サンプルコードの環境構築から実行してください。 - Ubuntuのバージョンはズレていても多分動きますが、動作に問題があればUbuntu22.04をインストールしてください。
本記事の環境構築手順は 2025-08-11 時点のものです。
最新のインストール手順が必要な場合は以下のWSL公式ドキュメント等を参照してください。
https://learn.microsoft.com/ja-jp/windows/wsl/install
前提条件
WSLコマンドを使用するには、以下のいずれかのバージョンを実行している必要があります:
- Windows 10 バージョン2004以降(ビルド19041以降)
- Windows 11(全バージョン)
それより前のバージョンの場合は、手動インストールが必要になります。
WSL公式ドキュメント 等を参照してください。
Ubuntu 22.04を指定してWSLをインストール
PowerShell またはコマンドプロンプトを管理者権限で開きます。
- スタートメニューで
PowerShellと検索 - 右クリックして
管理者として実行を選択
以下のコマンドを実行し、インストール可能なディストリ一覧に Ubuntu-22.04 が存在することを確認します。
wsl --list --online
以下のコマンドを実行します。このコマンドにより、WSLを実行するために必要な機能が有効になり、Ubuntu 22.04 LTSディストリビューションがインストールされます。
wsl --install -d Ubuntu-22.04
コマンド実行後、再起動を求められるのでパソコンを再起動してください。
環境構築(2): WSL2 に Ubuntu22.04.1 LTS をインストール
PowerShell を通常の権限で起動します。
- スタートメニューで
PowerShellと検索 - 左クリックして実行
PowerShell 上で以下のコマンドを実行して、正常にインストールされたことを確認します。
wsl -l -v
出力例は以下のようになります。
VERSION 列に 2 と表示されていれば WSL2 環境で実行されていることが確認できます。
PS C:\Users\hoge> wsl -l -v
NAME STATE VERSION
* Ubuntu-22.04 Running 2
PowerShell 上で以下のコマンドを実行します。
このコマンドにより WSL2 環境で Ubuntu-22.04 が起動します。
wsl -d Ubuntu-22.04
初回起動時には以下のようにユーザ名とパスワードの登録を求められます。
本記事とパスを揃えたい場合、ユーザ名は dmax-scratch を指定してください。
パスワードは sudo 権限でコマンドを実行する際に必要なので忘れないでください。
Ubuntu 22.04 LTS を起動しています...
Installing, this may take a few minutes...
Please create a default UNIX user account. The username does not need to match your Windows username.
For more information visit: https://aka.ms/wslusers
Enter new UNIX username: dmax-scratch
New password:
Retype new password:
passwd: password updated successfully
Installation successful!
Ubuntu22.04 への接続を終了するためには以下のコマンドを実行します。
exit
作成したユーザ dmax-scratch を利用して Ubuntu22.04 へ再接続するためには PowerShell 上で以下のコマンドを実行します。
wsl -d Ubuntu-22.04 -u dmax-scratch
環境構築(3): サンプルコードの環境構築
サンプルコードの実行環境を構築していきます。
ここからは Ubuntu22.04 環境にログインしていることを前提とします。
以下のコマンドを実行し、ユーザや作業ディレクトリを確認します。
# 現在のユーザを確認
whoami
# ホームディレクトリへ移動
cd ~
# 現在の作業ディレクトリを確認
pwd
実行すると以下のようになります。
$ whoami
dmax-scratch
$ cd ~
$ pwd
/home/dmax-scratch
以下のコマンドを実行して、Python のバージョン管理ツール uv をインストールします。
# uv のインストール
curl -LsSf https://astral.sh/uv/install.sh | sh
# uv へのパス設定の反映
source $HOME/.local/bin/env
# uv が利用可能になったか確認するため uv のバージョンを出力
uv --version
以下のように uv のバージョン情報が出力されればOKです。
$ uv --version
uv 0.8.8
次に、以下のコマンドを実行します。
このコマンドにより、サンプルコードをローカル環境にコピーし、uv により実行環境をセットアップします。
# ホームディレクトリへ移動
cd ~
# サンプルコードをダウンロード
git clone https://github.com/hotckrin/dmax-from-scratch-sample-code.git
# サンプルコードのディレクトリへ移動
cd dmax-from-scratch-sample-code
# uvで環境を自動構築
uv sync
以下のように Python 3.8 と pyomo 6.4.4 がインストールされたことが確認できればOKです。
$ uv sync
Using CPython 3.8.20
Creating virtual environment at: .venv
Resolved 3 packages in 3ms
Prepared 2 packages in 3.15s
Installed 2 packages in 21ms
+ ply==3.11
+ pyomo==6.4.4
次は動作確認をしていきます。
まず、 uv 経由で Python 3.8 の対話モードを起動してみます。
以下のように uv run python コマンドを実行し、Python 3.8 の対話モードが起動すればOKです。終了するには quit() コマンドか Ctrl-D キーを入力します。
$ uv run python
Python 3.8.16 (default, Mar 29 2023, 09:41:05)
[GCC 11.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
次に、サンプルコード dmax-mini-2.py の動作確認をします。
以下のように uv run dmax-mini-2.py コマンドを実行し、問題ファイルが出力されればOKです。
問題ファイルの存在は ls -lh | grep 2-problem のようにして確認できます。
# サンプルコードを実行して問題ファイルを出力
$ uv run dmax-mini-2.py
model for solving damage optimization problem
5 Set Declarations
const_total_equipment_type_index : Size=1, Index=None, Ordered=False
Key : Dimen : Domain : Size : Members
None : 1 : Any : 6 : {'arms', 'charm', 'head', 'legs', 'torso', 'waist'}
p_index : Size=1, Index=None, Ordered=False
Key : Dimen : Domain : Size : Members
None : 2 : p_index_0*p_index_1 : 442 : {('ラギアアームα', 'arms'), ('ラギアアームα', 'charm'),
...省略
# 問題ファイルの存在を確認
$ ls -lh | grep 2-problem
-rw-r--r-- 1 dmax-scratch dmax-scratch 458 Aug 11 14:42 dmax-mini-2-problem.col
-rw-r--r-- 1 dmax-scratch dmax-scratch 2.6K Aug 11 14:42 dmax-mini-2-problem.nl
-rw-r--r-- 1 dmax-scratch dmax-scratch 840 Aug 11 14:42 dmax-mini-2-problem.row
環境構築(4): SCIPソルバーの環境構築
最適化ソルバー SCIP の実行環境を構築していきます。
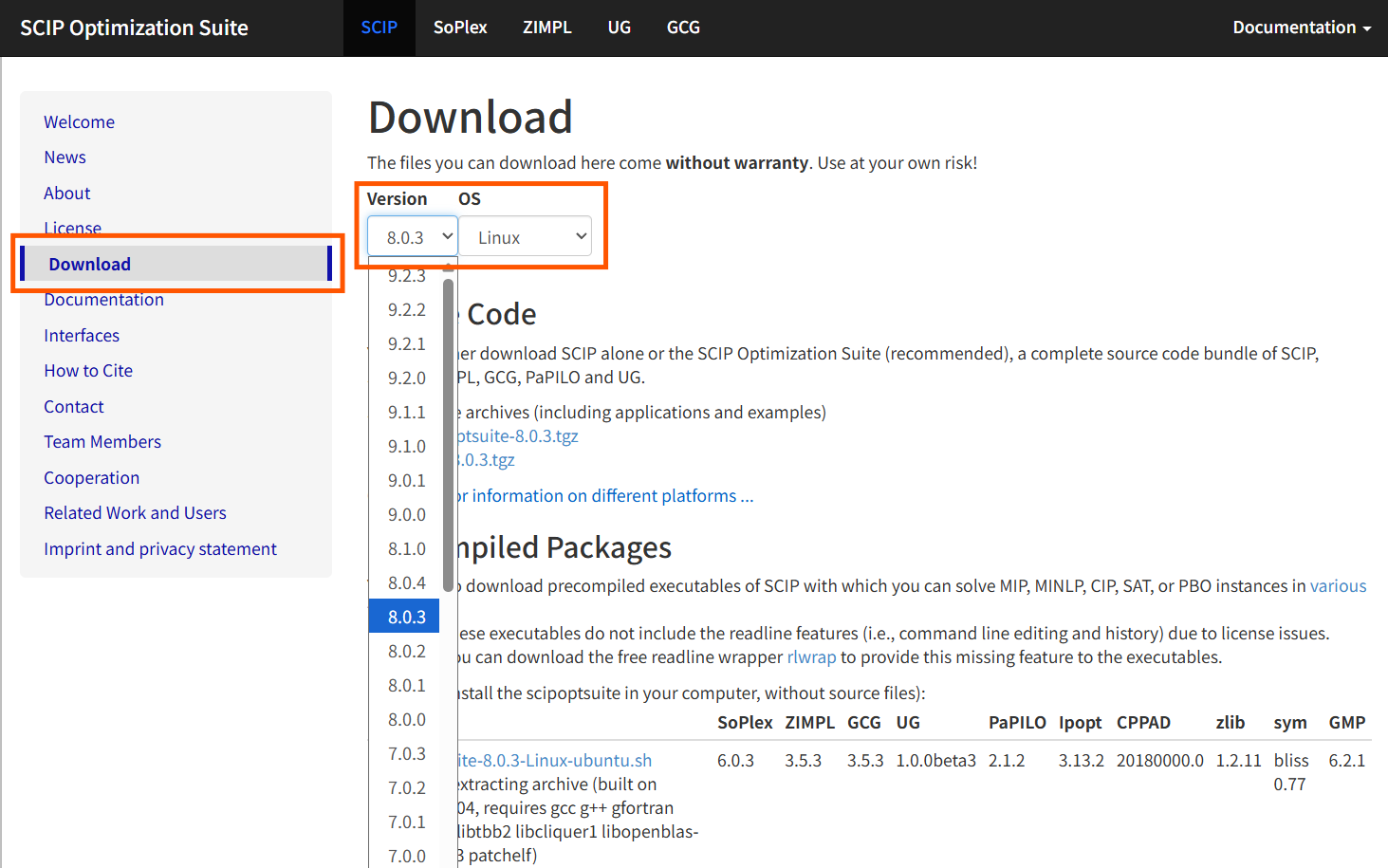
以下のSCIP公式ページにアクセスし、Download セクションを表示してください。
https://www.scipopt.org/index.php#download
ドロップダウンメニューから Version 8.0.3 と OS Linux を選択してください。
本記事ではソースコードからのビルドではなく、コンパイル済みパッケージを利用します。
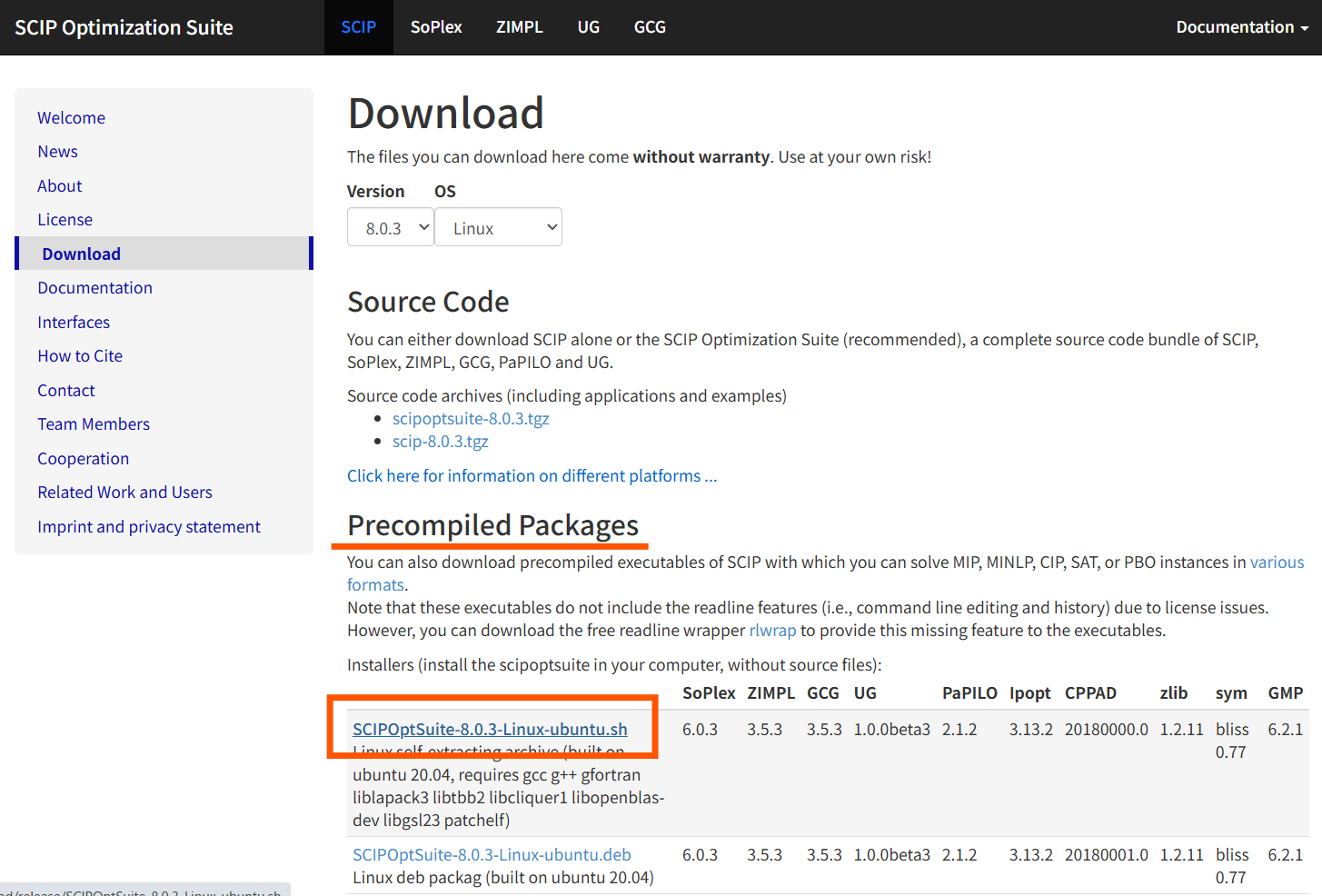
Precompiled Packages のセクションに SCIPOptSuite-8.0.3-Linux-ubuntu.sh のリンクがあることを確認します。
SCIPOptSuite-8.0.3-Linux-ubuntu.sh のリンクを右クリックし「リンクのアドレスをコピー」を選択します。
以下のコマンドを実行して、SCIP 8.0.3 のインストールスクリプトをダウンロードします。
# ホームディレクトリに移動
cd ~
# インストールスクリプトをダウンロード
wget <ここにコピーしたリンクを貼り付け>
# スクリプトがダウンロードできたか確認
ls -lh | grep SCIP
以下のように SCIPOptSuite-8.0.3-Linux-ubuntu.sh が確認できればOKです。
# wget のリンク例
$ wget https://www.scipopt.org/download/release/SCIPOptSuite-8.0.3-Linux-ubuntu.sh
...省略
# インストールスクリプトを確認
$ ls -lh | grep SCIP
-rw-r--r-- 1 dmax-scratch dmax-scratch 26M Dec 14 2022 SCIPOptSuite-8.0.3-Linux-ubuntu.sh
次に、SCIPの実行に必要な依存関係のパッケージをインストールします。
公式ドキュメント中の以下の記述から必要な依存パッケージを判断します。
SCIPOptSuite-8.0.3-Linux-ubuntu.sh
Linux self-extracting archive (built on ubuntu 20.04, requires gcc g++ gfortran liblapack3 libtbb2 libcliquer1 libopenblas-dev libgsl23 patchelf)
# パッケージリストを更新
# (sudo 実行時にパスワードを要求された場合はユーザ作成時のパスワードを入力)
sudo apt update
# SCIP8.0.3の実行に必要な依存関係をインストール
# (Ubuntu22.04 の標準環境では libgsl23 を見つけられないため libgsl27 を指定)
sudo apt install -y gcc g++ gfortran liblapack3 libtbb2 libcliquer1 libopenblas-dev libgsl27 patchelf
必要な依存パッケージがインストールできたので、次は先ほど wget でダウンロードしてきたSCIPのインストールスクリプトを実行します。
以下のコマンドを実行し、SCIPのインストールスクリプトを実行します。
sh SCIPOptSuite-8.0.3-Linux-ubuntu.sh
途中で聞かれる2つの質問には y と Y を入力します。(Do you accept the license? の質問については、公式ドキュメントからライセンスを確認しておいてください)
実行すると以下のようになります。Unpacking finished successfully と表示されていればOKです。
$ sh SCIPOptSuite-8.0.3-Linux-ubuntu.sh
SCIPOptSuite Installer Version: 8.0.3, Copyright (c) Zuse Institute Berlin
This is a self-extracting archive.
The archive will be extracted to: /home/dmax-scratch
If you want to stop extracting, please press <ctrl-C>.
Copyright 2002-2022 Zuse Institute Berlin
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
Do you accept the license? [yn]:
y
By default the SCIPOptSuite will be installed in:
"/home/dmax-scratch/SCIPOptSuite-8.0.3-Linux"
Do you want to include the subdirectory SCIPOptSuite-8.0.3-Linux?
Saying no will install in: "/home/dmax-scratch" [Yn]:
Y
Using target directory: /home/dmax-scratch/SCIPOptSuite-8.0.3-Linux
Extracting, please wait...
Relinking libraries
Unpacking finished successfully
SCIPソルバーのインストール場所を確認し、起動テストし、PATHに追加します。
# 改めてホームディレクトリにいることを確認
cd ~
# SCIPソルバーのインストール場所を確認
ls -lh SCIPOptSuite-8.0.3-Linux/bin/scip
# SCIPソルバーのバイナリを実行し、対話モードが起動することを確認
SCIPOptSuite-8.0.3-Linux/bin/scip
# quit または ctrl-D によりSCIPの対話モードを終了
quit
# SCIPソルバーのインストール場所の絶対パスを確認
realpath SCIPOptSuite-8.0.3-Linux/bin/
# ~/.bashrc にPATH設定を追記
echo "export PATH=\"$(realpath SCIPOptSuite-8.0.3-Linux/bin/):\$PATH\"" >> ~/.bashrc
# ~/.bashrc を反映してPATHを読み込む
source ~/.bashrc
# scip コマンドのみで SCIP 対話モードが起動するようになったことを確認
scip
最終的に以下のように scip コマンドのみで対話モードを起動できるようになればOKです。
$ scip
SCIP version 8.0.3 [precision: 8 byte] [memory: block] [mode: optimized] [LP solver: Soplex 6.0.3] [GitHash: 62fab8a2e3]
Copyright (C) 2002-2022 Konrad-Zuse-Zentrum fuer Informationstechnik Berlin (ZIB)
External libraries:
Soplex 6.0.3 Linear Programming Solver developed at Zuse Institute Berlin (soplex.zib.de) [GitHash: f900e3d0]
CppAD 20180000.0 Algorithmic Differentiation of C++ algorithms developed by B. Bell (github.com/coin-or/CppAD)
ZLIB 1.2.11 General purpose compression library by J. Gailly and M. Adler (zlib.net)
GMP 6.2.1 GNU Multiple Precision Arithmetic Library developed by T. Granlund (gmplib.org)
ZIMPL 3.5.3 Zuse Institute Mathematical Programming Language developed by T. Koch (zimpl.zib.de)
AMPL/MP 4e2d45c4 AMPL .nl file reader library (github.com/ampl/mp)
PaPILO 2.1.2 parallel presolve for integer and linear optimization (github.com/scipopt/papilo) [GitHash: 2fe2543]
bliss 0.77 Computing Graph Automorphism Groups by T. Junttila and P. Kaski (www.tcs.hut.fi/Software/bliss/)
Ipopt 3.13.2 Interior Point Optimizer developed by A. Waechter et.al. (github.com/coin-or/Ipopt)
user parameter file <scip.set> not found - using default parameters
SCIP>
次に、SCIP対話モードを便利にするために rlwrap をインストールします。
rlwrap を利用するとSCIP対話モードにおいて、コマンド履歴を遡ったり、ファイルの候補を補完したりできます。
# rlwrap をインストール
sudo apt install -y rlwrap
# rlwrap 経由で scip を起動できることを確認
rlwrap scip
# rscip というエイリアスを設定して、rlwrap 経由で scip を起動できるようにする
echo "alias rscip=\"rlwrap -f . -c -b '(){}[],=&^\$#@\\\";|\\\\' scip\"" >> ~/.bashrc
# 設定の反映
source ~/.bashrc
# rscip 一発で rlwrap 経由の scip 起動ができることを確認
rscip
以上でSCIP対話モードの準備ができました。
最後に、最適化問題ファイルを読み込んで最適化してみます。
以下のコマンドを実行し、SCIP対話モードで最適化できることを確認します。
# 問題ファイルが存在するディレクトリに移動
$ cd ~/dmax-from-scratch-sample-code/
# scip 対話モードを起動
$ rscip
# read コマンドで問題ファイルを読み込み
SCIP> read dmax-mini-2-problem.nl
# optimize コマンドで最適化
SCIP> optimize
# display solution コマンドで最適化の結果を表示
SCIP> display solution
実行すると以下のようになります。
q[反攻の護石Ⅲ] 1 (obj:0) のような結果装備の一覧が表示されればOKです。
$ rscip
SCIP version 8.0.3 [precision: 8 byte] [memory: block] [mode: optimized] [LP solver: Soplex 6.0.3] [GitHash: 62fab8a2e3]
Copyright (C) 2002-2022 Konrad-Zuse-Zentrum fuer Informationstechnik Berlin (ZIB)
External libraries:
Soplex 6.0.3 Linear Programming Solver developed at Zuse Institute Berlin (soplex.zib.de) [GitHash: f900e3d0]
CppAD 20180000.0 Algorithmic Differentiation of C++ algorithms developed by B. Bell (github.com/coin-or/CppAD)
ZLIB 1.2.11 General purpose compression library by J. Gailly and M. Adler (zlib.net)
GMP 6.2.1 GNU Multiple Precision Arithmetic Library developed by T. Granlund (gmplib.org)
ZIMPL 3.5.3 Zuse Institute Mathematical Programming Language developed by T. Koch (zimpl.zib.de)
AMPL/MP 4e2d45c4 AMPL .nl file reader library (github.com/ampl/mp)
PaPILO 2.1.2 parallel presolve for integer and linear optimization (github.com/scipopt/papilo) [GitHash: 2fe2543]
bliss 0.77 Computing Graph Automorphism Groups by T. Junttila and P. Kaski (www.tcs.hut.fi/Software/bliss/)
Ipopt 3.13.2 Interior Point Optimizer developed by A. Waechter et.al. (github.com/coin-or/Ipopt)
user parameter file <scip.set> not found - using default parameters
read dmax-mini-2-problem.nl
read problem <dmax-mini-2-problem.nl>
============
original problem has 17 variables (0 bin, 17 int, 0 impl, 0 cont) and 25 constraints
optimize
[linear] <const_skill_point[逆襲]>: <q[レギオスヘルムα]>[I] (+0) +<q[レギオスメイルα]>[I] (+0) >= 2;
;
violation: left hand side is violated by 2
all 1 solutions given by solution candidate storage are infeasible
presolving:
(round 1, fast) 7 del vars, 20 del conss, 0 add conss, 19 chg bounds, 0 chg sides, 0 chg coeffs, 0 upgd conss, 0 impls, 3 clqs
(round 2, fast) 12 del vars, 22 del conss, 0 add conss, 19 chg bounds, 0 chg sides, 0 chg coeffs, 0 upgd conss, 0 impls, 3 clqs
(0.0s) running MILP presolver
(0.0s) MILP presolver (2 rounds): 0 aggregations, 9 fixings, 0 bound changes
presolving (3 rounds: 3 fast, 1 medium, 1 exhaustive):
21 deleted vars, 25 deleted constraints, 0 added constraints, 19 tightened bounds, 0 added holes, 0 changed sides, 0 changed coefficients
0 implications, 0 cliques
transformed 1/1 original solutions to the transformed problem space
Presolving Time: 0.00
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes : 0
Primal Bound : +3.32000000000000e+02 (1 solutions)
Dual Bound : +3.32000000000000e+02
Gap : 0.00 %
display solution
objective value: 332
q[レギオスヘルムα] 1 (obj:64)
q[レギオスメイルα] 1 (obj:64)
q[レダゼルトアームγ] 1 (obj:68)
q[レダゼルトグリーヴγ] 1 (obj:68)
q[レダゼルトコイルγ] 1 (obj:68)
q[反攻の護石Ⅲ] 1 (obj:0)
SCIP>
おまけとして、rlwrap により Emacs ライクな Readline キーバインドが利用できることを確認します。これにより繰り返し操作や修正が楽になります。
# ctrl-P を入力するたびに1つ過去のコマンドを呼び出せることを確認
# ctrl-N を入力するたびに1つ先のコマンドに戻せることを確認
SCIP> # ここで ctrl-P or ctrl-N
# ctrl-R 入力後に read と入力すると直近の read コマンドを呼び出せることを確認
SCIP> # ここで ctrl-R → read → ctrl-E で確定
# TAB を2回入力すると候補ファイル名一覧が表示されることを確認
SCIP> read # ここで TAB x2
# ファイル名を途中まで入力した後 TAB を2回入力すると絞り込まれた候補ファイル一覧が表示されることを確認
SCIP> read dmax-mini-2-p # ここで TAB x2
対話モードではなく、SCIP ソルバーの起動時に問題ファイルを指定する方法もあります。
こちらを利用すると上記の対話モードで実行した操作を一発で実行できます。その代わり出力が多くて読みづらいと思います。
# ワンライナーで実行
$ scip -f dmax-mini-2-problem.nl
以上で、本記事で必要な全ての環境構築が完了しました。お疲れ様でした!
実装: dmax-practice.py
それでは Pyomo によるモデルを出力するためのコードを書いていきましょう。ファイル名は dmax-practice.py とします。
まずは最適化モデルを定義していくためのベースとなる Model クラスのインスタンスを作成します。
from pyomo.environ import *
# 線形計画問題を解くためのPyomoモデルを定義します
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
Pyomo の Model クラスには以下の2種類があります。
| モデルの種類 | 用途 |
|---|---|
ConcreteModel |
モデル定義の際にパラメータの値が分かる場合に利用 |
AbstractModel |
モデル定義の際にパラメータの値が分からず、最適化を実行する段階で判明する場合に利用 |
最適化モデルにおける変数は最適化処理で求める値なのでモデルを定義する際にはわかりません。
変数以外のパラメータ (定数) についてはモデルを定義する際に分かる場合と、最適化を実行する段階になるまで分からない場合の2種類があります。モデルを定義する際にパラメータが分かる場合には ConcreteModel を利用します。最適化を実行する段階になるまでパラメータの値が分からない場合には AbstractModel を利用します。
今回のようなモンハンの最適化シミュレーターの場合、パラメータとは具体的な装備やスキル等のゲーム内データにあたります。これらは、ゲーム内データやユーザの入力を元にモデルを定義する際に分かるものなので、今回は ConcreteModel を採用します。
Model クラスのインスタンス mdl を作成できたので、以降はこの mdl に変数やパラメータ、制約条件、目的関数の定義を追加していきます。
制約条件を表現するためには変数とパラメータが必要です。今回のようなシンプルな問題ではパラメータは制約条件に直書きすればいいですが、変数は最適化処理で変化しうるので先に定義しておく必要があります。なので、まずは変数を以下のように宣言しましょう。
from pyomo.environ import *
# 線形計画問題を解くためのPyomoモデルを定義します
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
# X_use: 非負整数変数
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
# Y_use: 非負整数変数
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
Pyomo の変数は Var クラスで定義します。
Var クラスの主な引数は以下の通りです。
| 引数 | 説明 |
|---|---|
domain または within
|
変数の取りうる値の範囲を指定 (実数、整数など) |
initialize |
変数の初期値を指定 |
引数 domain (within) では変数の取り得る値の範囲を指定します。取りうる値の範囲は Set と呼び、 Set としては Reals (実数), Integers (整数), NonNegativeIntegers (非負整数), Boolean (真偽値) などを指定できます。
定義済みの Set の一覧については Pyomo ドキュメント を参照してください。
within は domain のエイリアスなのでどちらでも良いです。domain を指定しなかった場合のデフォルト値は Reals (実数) になります。
今回の問題の場合、X_use と Y_use はともに非負整数という条件があるので NonNegativeIntegers を指定します。
0 <= X_use (ただし X_use は整数)
0 <= Y_use (ただし Y_use は整数)
引数 initialize では変数の初期値を指定します。初期値としては数値もしくは初期値を返すための関数を指定できます。
initialize で指定された値は最適化処理を行う際に解を探索する開始点として利用されます。
今回の問題の場合は非負整数であれば何でも良いので、初期値として0を指定しました。
このように作成した変数を mdl.X_use = という形でモデルの属性として追加しています。
Python ではドットに続く名前すべてを属性と呼びます。属性は他のプログラミング言語におけるメンバ変数、フィールド、メソッド、プロパティ等に似ています。
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
この mdl.X_use = の部分に馴染みがない方もいるかもしれません。ここでは Model クラスにおそらく存在しないであろう X_use という属性を勝手に定義しています。
これは Python の動的な属性追加という機能を利用しています。Python は実行時にオブジェクトに対して新しい属性を追加することができ、ここではそのように追加された属性を動的属性と呼んでいます。
Pyomo では変数のようなモデルを定義する要素を、モデルインスタンスへの動的属性によって追加することができます。変数だけではなく、パラメータ、制約条件、目的関数もすべて動的属性によってモデルに追加することができます。このような設計により Pyomo ではモデルにその変数や制約条件等が紐づいていることを直感的に表現することができます。
ここまでで、モデルに必要な変数を追加することができました。
次はこれらの変数を利用して制約条件をモデルに追加していきましょう。制約条件も動的属性を利用してモデルに追加していきます。
制約条件:
2 * X_use + 1 * Y_use >= 5
1 * X_use + 2 * Y_use <= 4
上記の制約条件は以下のようにモデルに追加できます。
from pyomo.environ import *
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
# 制約条件定義
# 制約1: 2 * X_use + 1 * Y_use >= 5
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
mdl.const_1 = Constraint(rule=constraint_1)
# 制約2: 1 * X_use + 2 * Y_use <= 4
def constraint_2(mdl):
return 1 * mdl.X_use + 2 * mdl.Y_use <= 4
mdl.const_2 = Constraint(rule=constraint_2)
Pyomo で制約条件を定義する際には Constraint クラスを利用します。Constraint クラスの引数 rule には制約条件の式を返す関数を指定します。
rule 引数に渡している関数 constraint_1 の定義を見ると、モデルに追加された変数 mdl.X_use と mdl.Y_use を利用して制約条件の不等式が定義されており、直感的に制約条件を定義できていることが分かると思います。
rule 引数に渡す関数の第1引数は常にモデルオブジェクトを受け取ります。そのため関数 constraint_1 を定義する際には以下のように mdl と記述して、第1引数にモデルを受け取るように定義する必要があります。
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
このようにして作成した制約条件を表す Constraint クラスのインスタンスを mdl.const_1 = という形で、動的属性によりモデルに追加しています。
mdl.const_1 = Constraint(rule=constraint_1)
rule 関数の戻り値としては基本的に制約式を返す必要があります。制約式は <=, >=, == を含む関係式により定義します。もし「防具の合計数が必ず1でなければならない」という制約がある場合は、以下のような == による制約式を定義することになるでしょう。
def constraint_armor_equal(mdl):
return mdl.X_use + mdl.Y_use == 1
ここまでで、変数と制約条件をモデルに追加できました。最後に目的関数をモデルに追加します。
50 + 50 * X_use + 40 * Y_use
上記の目的関数は以下のようにモデルに追加できます。
from pyomo.environ import *
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
# 制約条件定義
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
mdl.const_1 = Constraint(rule=constraint_1)
def constraint_2(mdl):
return 1 * mdl.X_use + 2 * mdl.Y_use <= 4
mdl.const_2 = Constraint(rule=constraint_2)
# 目的関数定義: 50 + 50 * X_use + 40 * Y_use を最大化
def objective_function(mdl):
return 50 + 50 * mdl.X_use + 40 * mdl.Y_use
mdl.OBJ = Objective(rule=objective_function, sense=maximize)
Pyomo で目的関数を定義する際には Objective クラスを利用します。 Objective クラスの取り扱いは Constraint とほぼ同じです。
引数 rule には目的関数の式を返す関数を指定します。Constraint の場合には、制約条件をを返すために等式や不等式を返す関数を指定していましたが、Objective の場合には、目的関数の式を返すため等号や不等号は必要ありません。
引数 sense には最適化の方向性として目的関数を最大化したいのか最小化したいのかを指定します。デフォルトは sense=minimize (最小化) なので、今回のような最大化の場合には明示的に sense=maximize と指定する必要があります。
このようにして作成した目的関数を、動的属性によりモデルに追加します。
mdl.OBJ = Objective(rule=objective_function, sense=maximize)
ここまでで、モデルの定義がすべて完了しました。最後にモデルをファイルに出力しましょう。
(ここで出力するファイルをSCIP ソルバーに入力することで最適解を得ることができます)
from pyomo.environ import *
# 線形計画問題を解くためのPyomoモデルを定義します
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
# X_use: 非負整数変数
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
# Y_use: 非負整数変数
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
# 制約条件定義
# 制約1: 2 * X_use + 1 * Y_use >= 5
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
mdl.const_1 = Constraint(rule=constraint_1)
# 制約2: 1 * X_use + 2 * Y_use <= 4
def constraint_2(mdl):
return 1 * mdl.X_use + 2 * mdl.Y_use <= 4
mdl.const_2 = Constraint(rule=constraint_2)
# 目的関数定義: 50 + 50 * X_use + 40 * Y_use を最大化
def objective_function(mdl):
return 50 + 50 * mdl.X_use + 40 * mdl.Y_use
mdl.OBJ = Objective(rule=objective_function, sense=maximize)
# 問題ファイルを出力
# symbolic_solver_labels を有効化して変数名等の情報を保持
mdl.write("dmax-practice-problem.nl", format="nl", io_options={'symbolic_solver_labels': True})
print("最適化問題のモデルをファイルを出力しました")
以下のように、モデルインスタンスの write メソッド mdl.write() を利用することで、定義したモデルをファイルに出力することができます。
mdl.write("dmax-practice-problem.nl", format="nl", io_options={'symbolic_solver_labels': True})
第1引数にはファイル名を指定します。
引数 format ではファイルの形式を指定できます。ここでは非線形問題にも対応している nl (AMPL Nonlinear) 形式を指定します。
引数 io_options では出力のオプションを指定できます。'symbolic_solver_labels': True によって、人間が読める形式のラベルがファイルに保存されるようになります。デバッグを行う際に便利なので指定しておきましょう。
以上で、最適化問題のモデルをファイルを出力するためのプログラム dmax-practice.py が完成しました。サンプルコードのリポジトリでは以下から dmax-practice.py を確認できます。
それではターミナルから dmax-practice.py を以下のようにして実行してみましょう。
dmax-practice-problem.* という名前のファイルが3つ出力されていれば成功です。
# プログラムを実行
$ uv run dmax-practice.py
最適化問題のモデルをファイルを出力しました
# ls コマンドでファイルが出力されたかどうか確認
$ ls -lh | grep dmax-practice-prob
-rw-r--r-- 1 dmax-scratch dmax-scratch 12 Aug 15 22:33 dmax-practice-problem.col
-rw-r--r-- 1 dmax-scratch dmax-scratch 747 Aug 15 22:33 dmax-practice-problem.nl
-rw-r--r-- 1 dmax-scratch dmax-scratch 20 Aug 15 22:33 dmax-practice-problem.row
出力されたファイルを眺めてみましょう。
# .nl ファイルの中身を確認 (出力は長いので省略)
$ cat dmax-practice-problem.nl
# .col ファイルに変数の名前が保存されていることを確認
$ cat dmax-practice-problem.col
X_use
Y_use
# .row ファイルに制約式や目的関数の名前が保存されていることを確認
$ cat dmax-practice-problem.row
const_1
const_2
OBJ
.nl 形式のファイルがメインのモデルファイルです。最適化ソルバーに入力する問題ファイルは .nl 形式のファイルになります。
では残りの .col や .row 形式のファイルは何かというと、Python プログラム中で指定した変数、制約式、目的関数の名前が出力されるファイルになります。io_options={'symbolic_solver_labels': True} を指定することによって、.col や .row 形式のファイルが出力されるようになります。これらのファイルがあると最適化問題の結果やモデルファイルが人間の読める形式で出力されるようになるため、結果の表示やデバッグに役立ちます。
次は最適化ソルバーに最適化問題を解かせてみます。
Python プログラムによって出力されたモデルのメインファイル dmax-practice-problem.nl をSCIPソルバーに入力して最適化してみましょう。
まず、SCIPソルバーを対話モードで起動します。
# rscip は rlwrap 経由で scip ソルバーを呼び出すエイリアス (環境構築(4): SCIPソルバーの環境構築 を参照)
$ rscip
SCIP version 8.0.3 [precision: 8 byte] [memory: block] [mode: optimized] [LP solver: Soplex 6.0.3] [GitHash: 62fab8a2e3]
Copyright (C) 2002-2022 Konrad-Zuse-Zentrum fuer Informationstechnik Berlin (ZIB)
External libraries:
Soplex 6.0.3 Linear Programming Solver developed at Zuse Institute Berlin (soplex.zib.de) [GitHash: f900e3d0]
CppAD 20180000.0 Algorithmic Differentiation of C++ algorithms developed by B. Bell (github.com/coin-or/CppAD)
ZLIB 1.2.11 General purpose compression library by J. Gailly and M. Adler (zlib.net)
GMP 6.2.1 GNU Multiple Precision Arithmetic Library developed by T. Granlund (gmplib.org)
ZIMPL 3.5.3 Zuse Institute Mathematical Programming Language developed by T. Koch (zimpl.zib.de)
AMPL/MP 4e2d45c4 AMPL .nl file reader library (github.com/ampl/mp)
PaPILO 2.1.2 parallel presolve for integer and linear optimization (github.com/scipopt/papilo) [GitHash: 2fe2543]
bliss 0.77 Computing Graph Automorphism Groups by T. Junttila and P. Kaski (www.tcs.hut.fi/Software/bliss/)
Ipopt 3.13.2 Interior Point Optimizer developed by A. Waechter et.al. (github.com/coin-or/Ipopt)
user parameter file <scip.set> not found - using default parameters
SCIP>
次に、以下のように read コマンドを実行してモデルファイル dmax-practice-problem.nl をSCIPソルバーに入力します。
読込結果から3つの変数 (variables) と2つの制約式 (constraints) があることがわかります。
Python プログラム中で定義した変数は X_use と Y_use の2つのみですが、.nl 形式では目的関数の定数項を変数として表現しているため変数が1つ増えています。
SCIP> read dmax-practice-problem.nl
read problem <dmax-practice-problem.nl>
============
original problem has 3 variables (0 bin, 2 int, 0 impl, 1 cont) and 2 constraints
読み込んだ問題の中身を表示するためには display problem コマンドを実行します。
display problem コマンドを実行すると以下のようになり、VARIABLES と CONSTRAINTS の部分に各変数や制約の詳細が表示されていることが確認できます。
SCIP> display problem
STATISTICS
Problem name : dmax-practice-problem
Variables : 3 (0 binary, 2 integer, 0 implicit integer, 1 continuous)
Constraints : 2 initial, 2 maximal
OBJECTIVE
Sense : maximize
VARIABLES
[integer] <X_use>: obj=50, original bounds=[0,+inf]
[integer] <Y_use>: obj=40, original bounds=[0,+inf]
[continuous] <objconstant>: obj=1, original bounds=[50,50]
CONSTRAINTS
[linear] <const_1>: +2<X_use>[I] +<Y_use>[I] >= 5;
[linear] <const_2>: <X_use>[I] +2<Y_use>[I] <= 4;
END
次に、以下のように optimize コマンドを実行して最適化を実行してください。
出力結果の SCIP Status : problem is solved [optimal solution found] から最適化が完了し、最適解が見つかったことが分かります。
SCIP> optimize
solution violates original bounds of variable <objconstant> [50,50] solution value <0>
all 1 solutions given by solution candidate storage are infeasible
presolving:
(round 1, fast) 2 del vars, 1 del conss, 0 add conss, 2 chg bounds, 0 chg sides, 0 chg coeffs, 0 upgd conss, 0 impls, 0 clqs
(round 2, fast) 2 del vars, 2 del conss, 0 add conss, 3 chg bounds, 0 chg sides, 0 chg coeffs, 0 upgd conss, 0 impls, 0 clqs
presolving (3 rounds: 3 fast, 1 medium, 1 exhaustive):
3 deleted vars, 2 deleted constraints, 0 added constraints, 3 tightened bounds, 0 added holes, 0 changed sides, 0 changed coefficients
0 implications, 0 cliques
transformed 1/1 original solutions to the transformed problem space
Presolving Time: 0.00
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes : 0
Primal Bound : +2.50000000000000e+02 (1 solutions)
Dual Bound : +2.50000000000000e+02
Gap : 0.00 %
最後に、以下のように display solution を実行して、得られた最適解を表示してください。
結果から目的関数を最大化する最適解は X_use=4, Y_use=0 (0なので表示されていない) の場合であり、目的関数の最大値は250になることが分かります。
SCIP> display solution
objective value: 250
X_use 4 (obj:50)
objconstant 50 (obj:1)
前のセクションでグラフを利用して、最適化を求めた結果と一致していることも確認できます。
以上の結果から、ゲーム内の条件が以下のような形式だった場合に、そのゲーム内で実現できる最大ダメージは250であり、実現するための装備は「防具Xのみ4つ装備」であることがわかりました。
武器C: 攻撃力 30, 属性値 20
防具X: 攻撃強化Ⅱ, 属性強化Ⅰ, 体術 x2, 重量1kg
防具Y: 攻撃強化Ⅰ, 属性強化Ⅱ, 体術, 重量2kg
スキルの効果:
攻撃強化Ⅰ: 攻撃力を +10 (装備全体で「攻撃強化Ⅰ」がN個ついている場合、攻撃力の加算値は +10*N とする。攻撃強化Ⅱ,属性強化Ⅰ,Ⅱについても同様)
攻撃強化Ⅱ: 攻撃力を +30
属性強化Ⅰ: 属性値を +20
属性強化Ⅱ: 属性値を +30
体術: ダメージ計算には寄与しない
装備の条件:
(条件1) 防具は0個以上のいくつでも装備できる
(条件2) 体術は最低5個欲しい
(条件3) 防具重量の合計の上限は4kg (4kg 以上の防具は重くて装備できない)
ダメージ計算式:
(ダメージ) = {(武器の攻撃力) + (攻撃強化スキルによる攻撃力加算)}
+ {(武器の属性値) + (属性強化スキルによる属性値加算)}
ここまでの流れで、最適化ソルバーにゲーム内の最適化問題を解かせることができました。
流れをまとめると
「ゲーム内の条件を制約式と目的関数に落とし込み、Python プログラムによって最適化問題をモデルとしてファイルに出力し、モデルファイルを最適化ソルバーに読み込ませて最適解を得る」という流れになっていました。
dmax-practice.py の実装では最適化問題の変数や制約条件の基本的な定義の仕方を確認しました。しかし、実際のゲーム内の膨大なデータや制約条件を表現するためにはまだ手数が足りません。 次のセクションでは DMAX を実装するための準備運動として、Pyomo の index, Var クラス, Param クラスを触ってみましょう。
実装: dmax-practice-index.py
先程のセクションでは以下のように、2つの変数をそれぞれ別々のVar クラスのインスタンスとして定義していました。以下の Var クラスのインスタンスはそれぞれ単一の変数を表しています。変数が2つ程度であればこのような定義でも問題ありませんが、変数の数が数千件レベルになるとツラくなります。
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
実は Var クラスはインデックスを利用することにより複数の変数をまとめて定義することができます。
上記の例では Var クラスの引数はすべて within=... のような = を含むキーワード引数として指定されていました。インデックスは位置引数として指定する必要があるので、すべてのキーワード引数の前に指定してください。それぞれの変数にはインデックスを指定することでアクセスできます。
# 位置引数にインデックスを指定することで複数の変数をまとめて定義
mdl.x = Var([0, 1], within=NonNegativeIntegers, initialize=0)
# 各変数にはインデックスでアクセス
mdl.x[0]
mdl.x[1]
上記2つの形式が同じ変数宣言になっていることを確かめてみましょう。先ほどはプログラムをファイルに書いて実行しましたが、今回は Python の対話モードを利用して Pyomo を触ってみましょう。
ターミナル上で以下のように実行して Python の対話モードを起動します。
$ uv run python
Python 3.8.16 (default, Mar 29 2023, 09:41:05)
[GCC 11.3.0] on linux
Type "help", "copyright", "credits" or "license" for more information.
>>>
Python の対話モードが起動したら以下のように実行してみてください。
# pyomo ライブラリをインポート
from pyomo.environ import *
# モデルを定義
mdl = ConcreteModel()
# 変数を別々の Var インスタンスとして定義
mdl.X_use = Var(within=NonNegativeIntegers, initialize=17)
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=17)
# 2の変数を1つの Var インスタンスとしてまとめて定義
mdl.x = Var([0, 1], within=NonNegativeIntegers, initialize=17)
# 変数 X_use の値や詳細を表示
mdl.X_use.value
mdl.X_use.pprint()
# インデックス付きの変数 mdl.x の値や詳細を表示
mdl.x[0]
mdl.x.pprint()
# ループ処理も可能
for index in range(0, 2):
mdl.x[index].value
実際に実行すると以下のようになります。
mdl.x[0] のようにアクセスすると各変数にアクセスできるため、配列のように扱えることが確認できます。
# 単一の変数 X_use の値は初期値17に設定されています
>>> mdl.X_use.value
17
# 変数 X_use の詳細を表示してみると、下限、初期値、上限、範囲などがわかります
>>> mdl.X_use.pprint()
X_use : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 17 : None : False : False : NonNegativeIntegers
# インデックス付きの変数 x ではインデックスを指定することで個々の変数にアクセスできます
# x[0] も初期値は17に設定されていることがわかります
>>> mdl.x[0].value
17
# インデックス付きの変数 x の全体の詳細を表示すると、key=0,1 に対してそれぞれ変数が定義されていることが確認できます
>>> mdl.x.pprint()
x : Size=2, Index=x_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
0 : 0 : 17 : None : False : False : NonNegativeIntegers
1 : 0 : 17 : None : False : False : NonNegativeIntegers
# インデックスでアクセスできるのでループ処理も可能です
>>> for index in range(0, 2):
... mdl.x[index].value
...
17
17
次はパラメータを定義するための Pyomo のクラス Param を利用してみましょう。
最適化問題を解く際に、変化しない値 (定数) を Pyomo では Param クラスで表現します。
先程の問題の例で言うと、制約条件や目的関数に登場する 2 * X_use の 2 のような定数部分をパラメータで表現することを考えます。
2 * X_use + 1 * Y_use >= 5
前のセクションでは、上記の制約条件を以下のように表現していました。
これはパラメータを実際の数値として制約条件の式に直書きしている形になります。
# 制約条件定義
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
こちらを Param を使って書き直すと以下のようになります。
# pyomo ライブラリをインポート
from pyomo.environ import *
# モデルを定義
mdl = ConcreteModel()
# 変数定義
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
# パラメータ定義
mdl.p = Param(initialize=2)
mdl.q = Param(initialize=1)
mdl.r = Param(initialize=5)
# 制約式
def constraint_1(mdl):
return mdl.p * mdl.X_use + mdl.q * mdl.Y_use >= mdl.r
# モデルに制約式を追加
mdl.const_1 = Constraint(rule=constraint_1)
# モデルの定義を出力
mdl.pprint()
実際に実行してみると以下のような結果になります。
3 Param Declarations の部分を見ると、3つのパラメータ (p=2, q=1, r=5) がモデルに追加されていることがわかります。
1 Constraint Declarations の部分を見ると、制約式において Param で定義したパラメータの値が反映されていることが分かります。
# モデル定義を出力
>>> mdl.pprint()
3 Param Declarations
p : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 2
q : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 1
r : Size=1, Index=None, Domain=Any, Default=None, Mutable=False
Key : Value
None : 5
2 Var Declarations
X_use : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 0 : None : False : False : NonNegativeIntegers
Y_use : Size=1, Index=None
Key : Lower : Value : Upper : Fixed : Stale : Domain
None : 0 : 0 : None : False : False : NonNegativeIntegers
1 Constraint Declarations
const_1 : Size=1, Index=None, Active=True
Key : Lower : Body : Upper : Active
None : 5.0 : 2*X_use + Y_use : +Inf : True
6 Declarations: X_use Y_use p q r const_1
次は、Var の場合と同様に Param でもインデックスを利用してパラメータを定義してみましょう。
Var と同様に Param のインデックスも位置引数として、全てのキーワード引数の前に指定します。
# pyomo ライブラリをインポート
from pyomo.environ import *
# モデルを定義
mdl = ConcreteModel()
# 変数定義
mdl.x = Var([0, 1], within=NonNegativeIntegers, initialize=0)
# パラメータ定義
mdl.p = Param([0, 1, 2], initialize={0: 2, 1: 1, 2: 5}, within=Integers, default=0)
# インデックス付きパラメータの詳細表示
mdl.p.pprint()
# インデックスを指定してアクセス可能
for i in range(0, 3):
mdl.p[i]
# 制約条件定義
def constraint_1(mdl):
return mdl.p[2] <= sum(mdl.p[i] * mdl.x[i] for i in range(0,2))
mdl.const_1 = Constraint(rule=constraint_1)
# モデル定義を出力
mdl.pprint()
関数 sum() の内部の mdl.p[i] * mdl.x[i] for i in range(0, 2) の部分は リスト内包記法 (または ジェネレータ式) と呼ばれる書き方です。i = 0, 1 のすべての場合について、 mdl.p[i] * mdl.x[i] という要素を持つ配列を生成しています。つまり以下の2つの式は同等です。リスト内包記法とインデックスを組み合わせると、大量のパラメータと変数をループ処理で生成できるようになるため非常に役立ちます。
# リスト内包記法 (ジェネレータ式)
sum(mdl.p[i] * mdl.x[i] for i in range(0,2))
# 展開した形
sum((mdl.p[0] * mdl.x[0]) + (mdl.p[1] * mdl.x[1]))
次は、Param を2次元配列で定義してみましょう。
Pyomo の2次元配列は data_info[0][1] でアクセスするような入れ子形式ではなく、data_info[0, 1] のようなタプルキーでアクセスする形式を利用します。一般に後者の形式のほうが高速にアクセスできるため最適化されたライブラリで利用されることが多いです。
インデックスは1次元配列のときと同様に Param クラスの位置引数として指定しています。2次元配列の場合は位置引数に2つのインデックスを指定します。本記事では利用しませんが、3次元以上の高次元配列も同じ要領で定義できます。
# pyomo ライブラリをインポート
from pyomo.environ import *
# モデルを定義
mdl = ConcreteModel()
# タプルキーで2次元配列を定義
data_info = {
('key1', 0): 2,
('key1', 1): 1,
('key1', 2): 5,
('key2', 0): -2,
('key2', 1): -1,
('key2', 2): -5,
}
# 位置引数にインデックスを2つ指定し、このインデックスで引ける2次元配列をキーワード引数 initialize に指定
mdl.p = Param(['key1', 'key2'], [0, 1, 2], initialize=data_info, within=Integers, default=0)
# パラメータ p の詳細を確認
mdl.p.pprint()
# インデックスによるアクセスでループ処理
for key in ['key1', 'key2']:
for i in range(0, 3):
mdl.p[key, i]
Python の対話モードを起動し、実際に実行すると以下のようになります。
パラメータ p の詳細を表示すると ('key1', 0) : 2 のように出力されており、タプルキー ('key1', 0) に対して値 2 が設定されていることがわかります。
また、二重 for ループの実行結果を見ると、インデックスの組み合わせ (タプルキー) によってすべての要素にアクセスできていることがわかります。
>>> mdl.p.pprint()
p : Size=6, Index=p_index, Domain=Integers, Default=0, Mutable=False
Key : Value
('key1', 0) : 2
('key1', 1) : 1
('key1', 2) : 5
('key2', 0) : -2
('key2', 1) : -1
('key2', 2) : -5
>>> for key in ['key1', 'key2']:
... for i in range(0, 3):
... mdl.p[key, i]
...
2
1
5
-2
-1
-5
ここまでで、インデックスと Var クラス、 Param クラスを利用して大量の変数やパラメータを定義&利用する方法を見てきました。
最後に、前のセクションで定義した Pyomo モデルをインデックスと Param クラスを利用して書き直してみましょう。インデックスと Param クラスを利用したコードを dmax-practice-index.py というファイルで保存します。
サンプルコードのリポジトリでは以下から dmax-practice-index.py を確認できます。
インデックスや Param クラスを利用しないコード
from pyomo.environ import *
# モデル定義
mdl = ConcreteModel(name="dmax-practice", doc="dmax-practice: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
# X_use: 非負整数変数
mdl.X_use = Var(within=NonNegativeIntegers, initialize=0)
# Y_use: 非負整数変数
mdl.Y_use = Var(within=NonNegativeIntegers, initialize=0)
# 制約条件定義
# 制約1: 2 * X_use + 1 * Y_use >= 5
def constraint_1(mdl):
return 2 * mdl.X_use + 1 * mdl.Y_use >= 5
mdl.const_1 = Constraint(rule=constraint_1)
# 制約2: 1 * X_use + 2 * Y_use <= 4
def constraint_2(mdl):
return 1 * mdl.X_use + 2 * mdl.Y_use <= 4
mdl.const_2 = Constraint(rule=constraint_2)
# 目的関数定義: 50 + 50 * X_use + 40 * Y_use を最大化
def objective_function(mdl):
return 50 + 50 * mdl.X_use + 40 * mdl.Y_use
mdl.OBJ = Objective(rule=objective_function, sense=maximize)
# 問題ファイルを出力
# symbolic_solver_labels を有効化して変数名等の情報を保持
mdl.write("dmax-practice-problem.nl", format="nl", io_options={'symbolic_solver_labels': True})
print("最適化問題のモデルをファイルを出力しました")
インデックスと Param クラスを利用して書き直したコード
from pyomo.environ import *
# モデル定義
mdl = ConcreteModel(name="dmax-practice-index", doc="dmax-practice-index: ゼロから作るモンハン最適化シミュレータ")
# 変数定義
mdl.x = Var([0, 1], within=NonNegativeIntegers, initialize=0)
p_dict = {
(0, 0): 2,
(0, 1): 1,
(0, 2): 5,
(1, 0): 1,
(1, 1): 2,
(1, 2): 4,
}
q_dict = {
0: 50,
1: 40,
2: 50,
}
# パラメータ定義
mdl.p = Param([0, 1], [0, 1, 2], initialize=p_dict, within=Integers, default=0)
mdl.q = Param([0, 1, 2], initialize=q_dict, within=Integers, default=0)
# 制約条件定義
# 制約1: 2 * X_use + 1 * Y_use >= 5
def constraint_1(mdl):
return sum(mdl.p[0, i] * mdl.x[i] for i in [0, 1]) >= mdl.p[0, 2]
mdl.const_1 = Constraint(rule=constraint_1)
# 制約2: 1 * X_use + 2 * Y_use <= 4
def constraint_2(mdl):
return sum(mdl.p[1, i] * mdl.x[i] for i in [0, 1]) <= mdl.p[1, 2]
mdl.const_2 = Constraint(rule=constraint_2)
# 目的関数定義: 50 * X_use + 40 * Y_use + 50 を最大化
def objective_function(mdl):
return sum(mdl.q[i] * mdl.x[i] for i in [0, 1]) + mdl.q[2]
mdl.OBJ = Objective(rule=objective_function, sense=maximize)
# 問題ファイルを出力
# symbolic_solver_labels を有効化して変数名等の情報を保持
mdl.write("dmax-practice-index-problem.nl", format="nl", io_options={'symbolic_solver_labels': True})
print("最適化問題のモデルをファイルを出力しました")
ここで、「変数である Var はともかく、定数はわざわざ Param クラスを利用しなくてもモデルを定義できるのではないか?」という疑問が浮かぶかもしれません。これはその通りで、実際に dmax-practice.py では Param クラスを利用せずにモデルを定義していますし、パラメータ数が多い場合でも dict や list を利用すれば対応できます。
しかし、Pyomo では定数 (パラメータ) を定義するために Param クラスを利用するのがベストプラクティスになります。理由は Param クラスを利用してパラメータを Pyomo モデルの一部として管理することにより、整合性のチェックが可能になり、デバッグしやすくなるからです。
例えば、mdl.pprint() を利用すると Param クラスで登録した内容をモデルの一部として表示できますし、Param クラスのインデックスと initialize= のデータに不整合があればエラーが出力されます。
したがって、パラメータを定義する際にはまず Param クラスとして定義することを考えてください。
モンハンワイルズの最適化シミュを自作する
次は、実際のモンハンワイルズのデータを利用して最適化シミュレーターを作成していきます。
この章で実装する最適化シミュの名前は dmax-mini と呼ぶことにします。dmax-mini では装備やスキルの種類こそ絞りますが、実際の最適化シミュ DMAX MHWilds で考慮している制約条件をすべて実装していきます。なので dmax-mini をベースに対応するデータを拡張していけば DMAX MHWilds と同じ最適化シミュを実装できます。
制約条件
まず、モンハンワイルズにおける最適化シミュの制約条件を整理します。自然言語で記述すると以下のようになります。
普通にゲームをしていると特に意識することはありませんが、モンハンワイルズには以下の6個の制約条件があります。ダメージ計算式に加えて以下の6つの制約条件を全て実装すると最適化シミュが完成します!
| 制約条件 | 制約内容 |
|---|---|
| 制約条件(1) | 各部位で装備できる個数は1以下 (部位は次の7つ 頭・胴・腕・腰・脚・護石・武器) |
| 制約条件(2) | ユーザが指定したスキルレベルの条件を満たす |
| 制約条件(3) | 装飾品はスロットレベル以上の大きさのスロットにしか装着できない |
| 制約条件(4) | ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ |
| 制約条件(5) | ダメージ計算式において有効なスキルは装備中のスキルのみ |
| 制約条件(6) | 会心率の上限は100% |
いくつかの条件について補足します。
制約条件(2): ユーザが指定したスキルレベルの条件を満たす
この条件(2)はスキルシミュレーターの入力を想像してもらうとわかりやすいです。ユーザはただ火力の高い装備が欲しいわけではなく、その武器を運用する上で欲しいスキルを満たした上で火力の高い装備が欲しいのです。そのためユーザが入力した「各スキルについて最低限満たしてほしいスキルレベル」という条件を満たす必要があります。
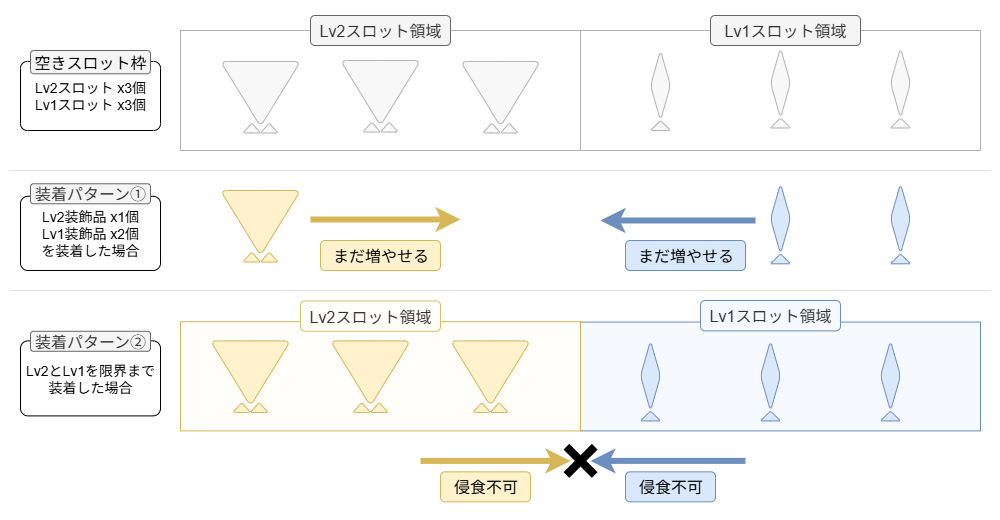
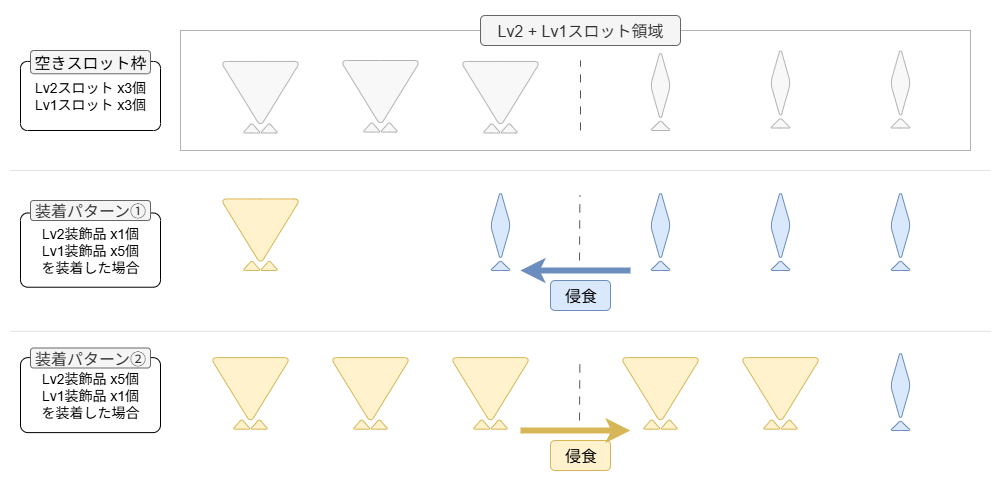
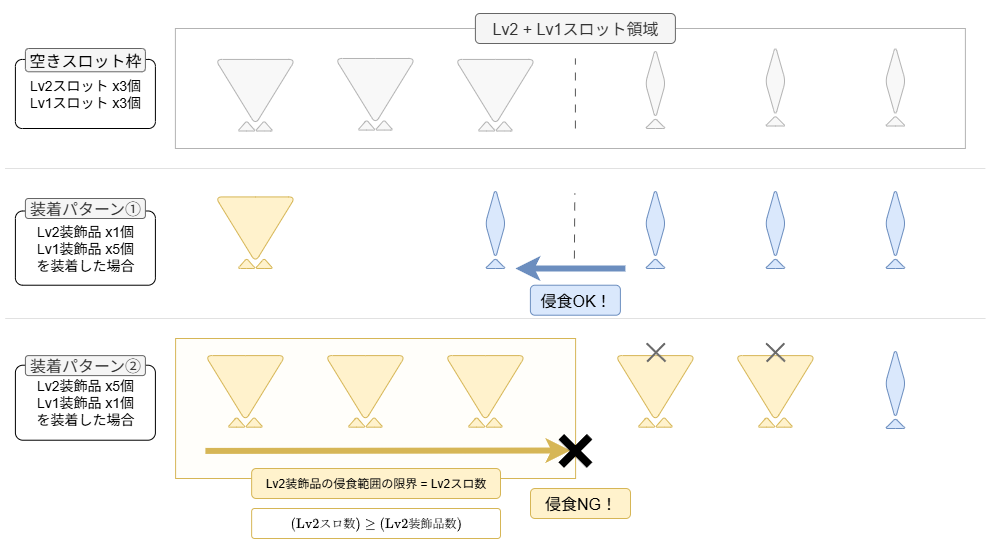
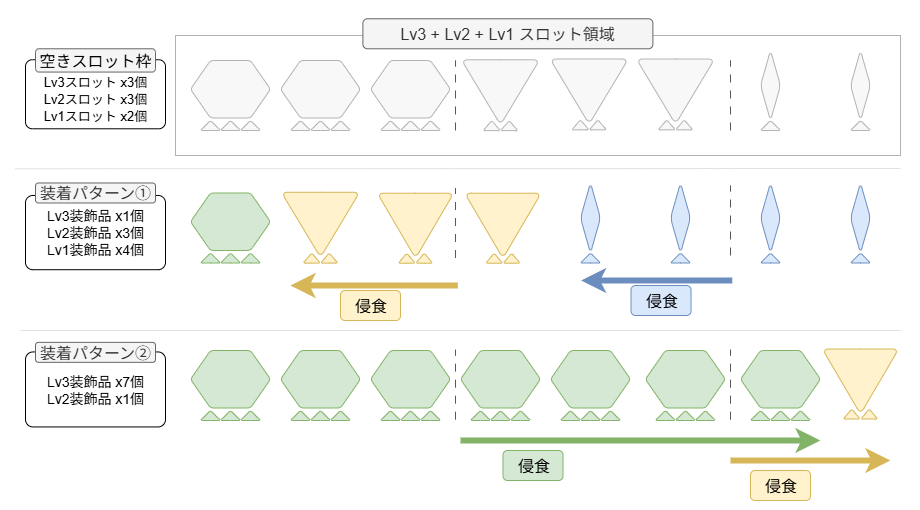
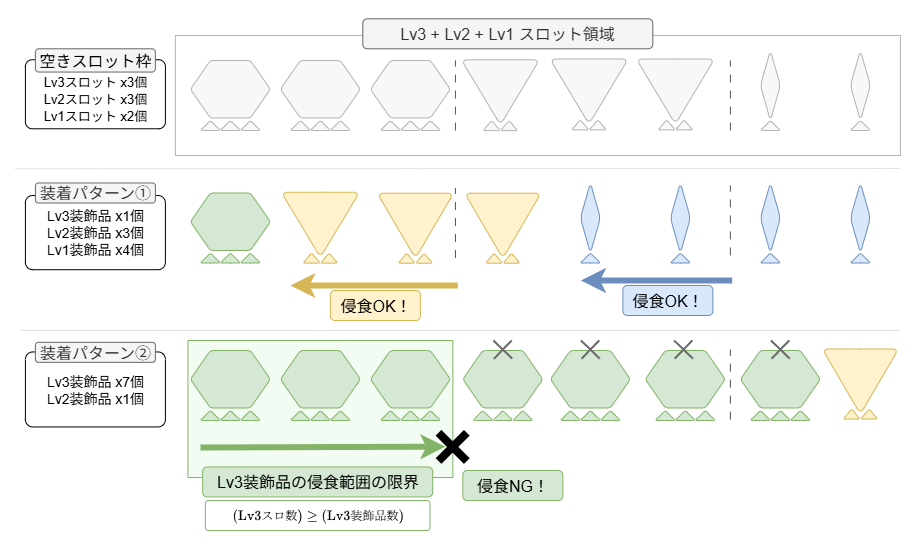
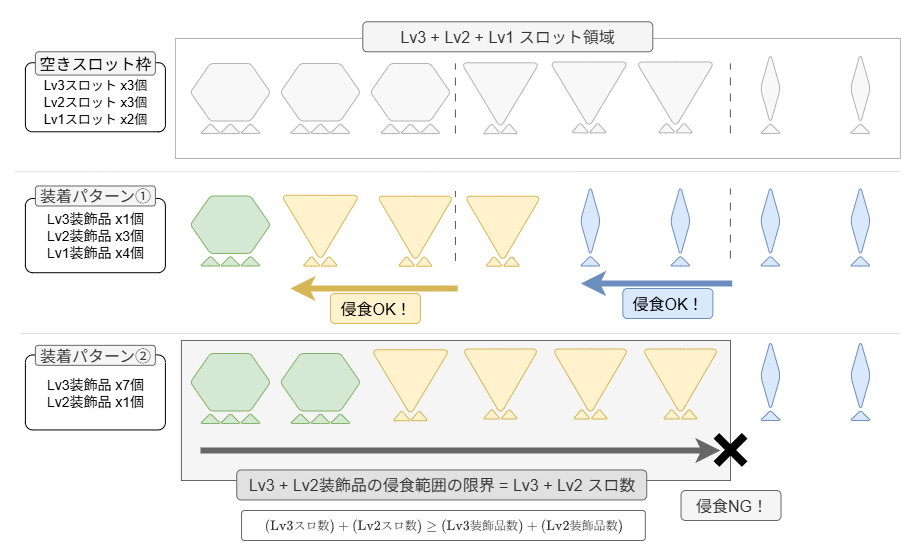
制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
条件(3)は装飾品のルールを示しています。これは例えば、「ある装飾品のスロットレベルが 2 なのであれば、装備のLv3スロットとLv2スロットには着けられるが、Lv1スロットには着けられない」のようなルールのことです。装飾品ルールを式に落とし込むのが一番難しいので、後に詳しく解説します。
制約条件(4): ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ
条件(4)は当たり前過ぎて逆にわかりにくいかもしれません。条件(4) は例えば、装備全体で「弱点特効Lv5」が発動している場合、ダメージ計算式においては弱点特効Lv5の効果 (会心率+30%) のみが発動し、弱点特効Lv4 ~Lv1 の効果は発動しない、という条件を示しています。これは実際のゲーム上のルールでもあるのですが、ダメージ計算式の実装に依存して出てくる条件でもあるので、後ほど登場するダメージ計算式の実装を見ると必要性がわかりやすいと思います。
制約条件(5): ダメージ計算式において有効なスキルは装備中のスキルのみ
条件(5) も当たり前ですね。条件(5) は例えば、ダメージ計算式において「弱点特効Lv5」の効果が発動するためには、装備している装備全体において弱点特効Lv5を満たす必要がある、という条件を示しています。こちらも実装依存で登場する面があります。
それでは制約条件を順番に式に落とし込み、実装していきましょう。
💡 動くものを小さく作る
この記事では説明のために制約条件を天下り式に提示しました。しかし実際に新しいシミュレーターを実装するときには、はじめから制約条件を綺麗に割り出すことは難しいです。プログラムには実際に実行して試すことができるという嬉しい性質があります。制約条件があっているかわからないときはとりあえず実装して、いい感じの結果がでてくるかどうか試し、必要に応じて修正するというアプローチが有効です。幸いモンハンの最適化問題は複雑なので、実装が間違っていればデタラメな結果が返ってくる可能性が高いです。なので、良い結果が返ってくるまで実行&修正を繰り返すという手段は有効です。
最適化シミュのような大きめのプログラムを一人で書くときのコツは、とりあえず動くものを小さく作る です。まずは最小構成で動くものを作り、動作を保ちながら不足機能を追加していくというアプローチが有効です。
逆に、はじめから完璧な絵を描いて計画通りに実装するというアプローチは、途中で修正が必要になる可能性が高く、最初の計画に時間をかけるのは割に合わないことが多いです。(人と分業するときにはそうも言ってられないのですが...)
実際に私が実装したときも、最初から制約条件を綺麗に思いついたわけではなく、実装してみて、足りないところを修正してというループを何度か繰り返してシミュを完成させました。記事を書くにあたって制約条件を整理してみたら上記の6つに整理できた、というのが正しいです。
dmax-mini-1.py
制約条件(1), (2) を定式化するために、まずはモンハンの最適化シミュにおける「解の候補」と「最適解」とはなにかを考えてみましょう。
簡単のために装備データは「防具シリーズ2種類, 護石2種類, 装飾品2種類」に絞って考えます。また、腰防具と脚防具は除外して考えます。
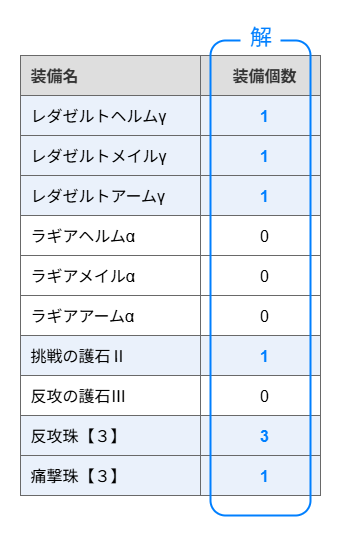
モンハンワイルズの最適化シミュにおける解の候補は以下のようなテーブルで表現できます。
各行が、各装備を何個装備するのかを示してます。上記テーブルの例では、「レダゼルトγシリーズ一式に挑戦の護石Ⅱを装備し、スロットに装飾品を4つ着けた装備」を示しています。
テーブルの装備個数の列は1つの解を示しています。
装備しない装備の行を削除してはいけません。なぜなら「装備しない」という情報が解の構成要素になっているからです。そのため (装備しない) = (装備個数が0個) として扱っています。
また、装備するか否かのような真偽値ではなく、装備個数という整数値で管理している点も重要です。これによって、装備するか否かを 0, 1 で扱えるだけでなく、装飾品のような複数装備できる装備も扱えるようになります。
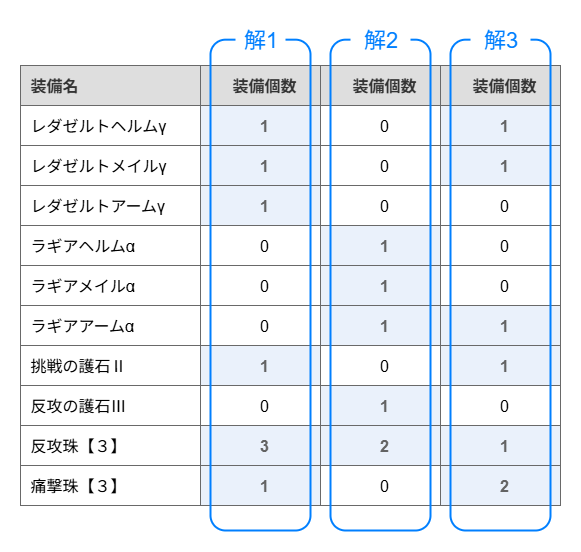
解候補は以下のような「各装備をそれぞれ何個使用するか?」を表した組み合わせとして表現できます。
(レダゼルトヘルムγ, レダゼルトメイルγ, ... , 反攻珠【3】, 痛撃珠【3】) =
(1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 3, 1)
このような、「各装備データをそれぞれ何個装備するか?」という形式で解の候補を定義すると、数式やコンピュータが処理しやすい形式になります。処理しやすくなる理由は条件分岐が消えて同じ形式で扱えるようになるからです。防具数は膨大なので、最適化シミュを実装する際に、「ラギアヘルムαを装備しなかった場合~」などと if 文による条件分岐処理を書いていてはキリがありません。「ラギアヘルムαを装備しなかった場合」を「ラギアヘルムαの装備個数0個」と表現することにより、すべてのパターンを1つの組み合わせで表現できます。
他の解の候補としては以下のような例が挙げられます。
(レダゼルトヘルムγ, レダゼルトメイルγ, ... , 反攻珠【3】, 痛撃珠【3】) =
(1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 3, 1)
(0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 2, 0)
(1, 1, 0, 0, 0, 0, 0, 1, 1, 1, 1, 0, 1, 2)
よって、最適化シミュにおける最適解とは上記のような「各装備をそれぞれ何個使用するか?」を表す組み合わせのうち、ゲーム内の条件を満たす解候補を全て比較したときに、ダメージ計算式が最大になる解と表現できます。
💡 全探索と枝刈り
時間さえ許せば、全ての解候補を総当りすることで最適解を求めることができます。解候補を全てリストアップし、それぞれがゲーム内の条件を満たすか検証し、満たす場合はダメージ計算式を適用して最大ダメージがでる解を特定すればいいわけです。
しかし、実際のデータは膨大なので総当たり戦略は現実的ではありません。仮に装飾品も複数装備できないとすれば、各装備データを使用するか否かで2通りあるので、$(装備数)^2$ 通り試さなくてはなりません。装備数が100個程度でも $1.2 \times 10^{30}$ 通りあります。現代のコンピュータは1秒あたり $10^9$ 回程度しか処理できないため、これを待つのは現実的ではありません。装備数が増えることによって、試すべき解候補が指数関数的に増大するため実質的に解けなくなってしまいます。
総当たりでは間に合いませんでしたが、実際はもっと工夫ができます。例えば、頭装備をどれか装備するのであれば他の頭装備は装備できませんから、この場合は他の頭装備を除外できます。なので実際には $(装備数)^2$ 通りも試さなくて良いわけです。このように解候補を絞っていく操作は枝刈りと呼ばれています。
枝刈りによって解候補をしぼっていくというのも最適シミュを実装するための1つのアプローチです。実際に、モンハンのスキルシミュレーターにはこの枝刈りアプローチで実装されているものもあるようです。しかし、枝刈り処理を考えて正しく組むのは難しいです。ゲームが変われば枝刈りのアプローチも変わってしまいます。
それに対して最適化ソルバーを利用すると、枝刈りに相当する最適化処理は全てソルバーが考えてくれるので、個々のゲームの制約に対して個別の処理を実装する必要はなくなります。その代わり、ゲームの制約を制約条件式に落とし込む必要はあります。つまり、最適化ソルバーは1つ抽象度の高いレイヤーで最適化問題を扱えるということになります。
これで解の候補を表現することができました。この解の候補は変数としてモデルに追加します。
制約条件を書くためには解の変数に加えて、装備の属性データ が必要になります。
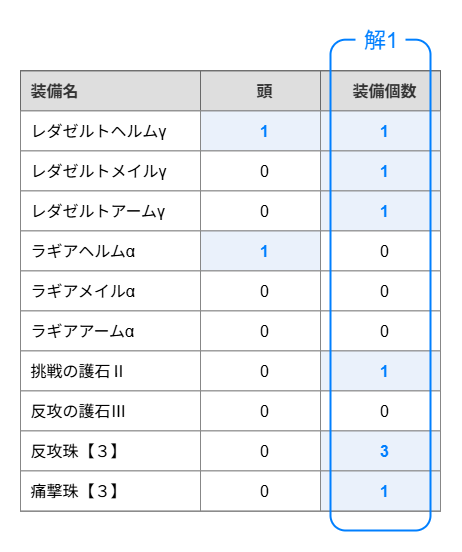
例えば「頭防具は1個以下しか装備できない」という制約条件を表すためには、「どの装備が頭防具であるのか?」を示すデータが必要です。先程のテーブルに新しい列として 頭 という属性を追加し、各防具の頭属性データを入力してみると以下のようになります。
ここで、制約条件(1) のために、解1における頭装備の合計数を計算するにはどうすればよいでしょうか?
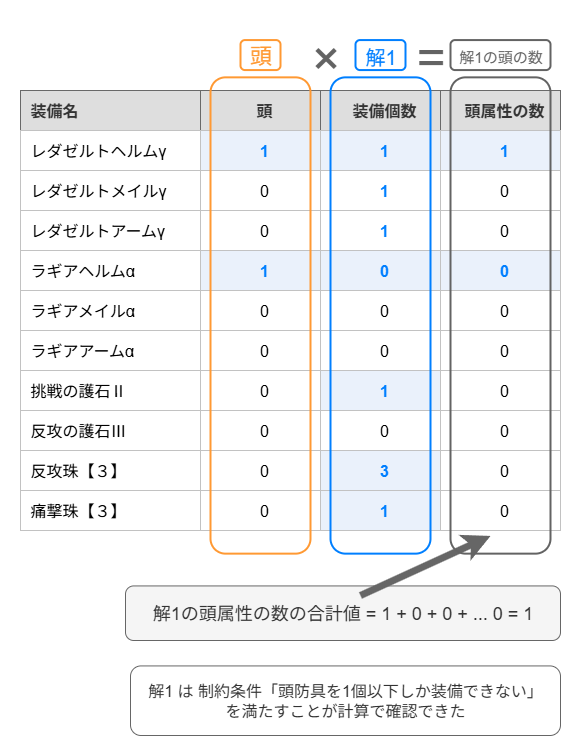
制約条件(1): 各部位の装備は1つ以下しか装備できない
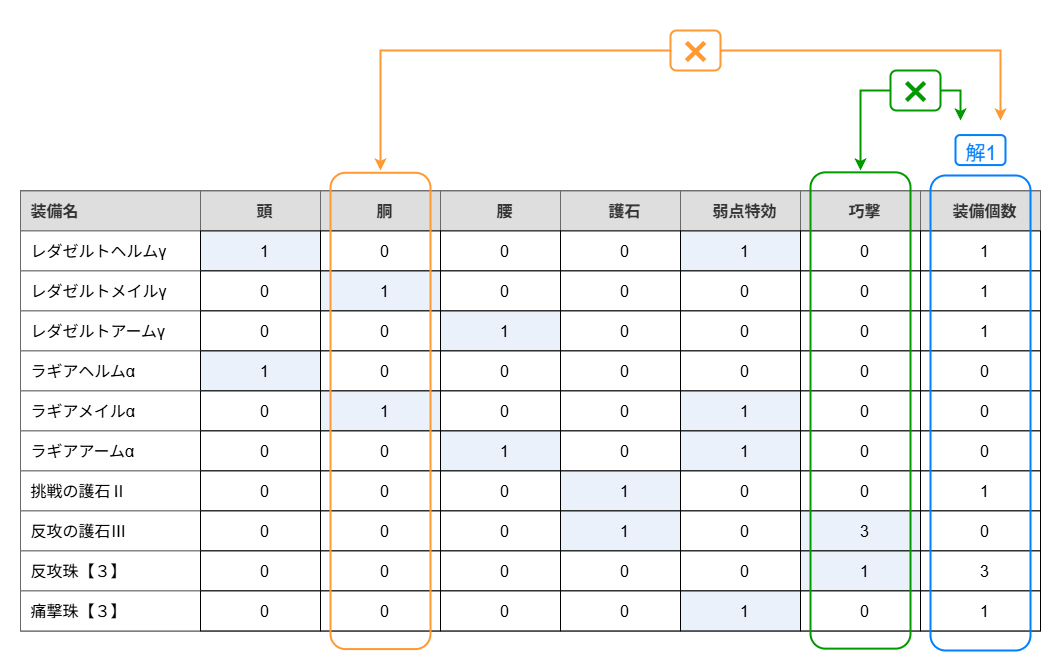
行ごとに 頭 属性の列 と 装備個数 の値を掛け算した結果を、新しい列 頭属性の数 に書くと以下のようになります。さらに 頭属性の数 の列の値の和を計算すると、解1 における頭防具の数が計算できます。解1 の場合、頭防具の合計数は 1 であり、モンハンワイルズの制約条件「頭防具を1個以下しか装備できない」を満たしている解であることがわかります。
(解1における頭装備の合計数) = (各行における
頭列と装備個数列の数値の積の和)
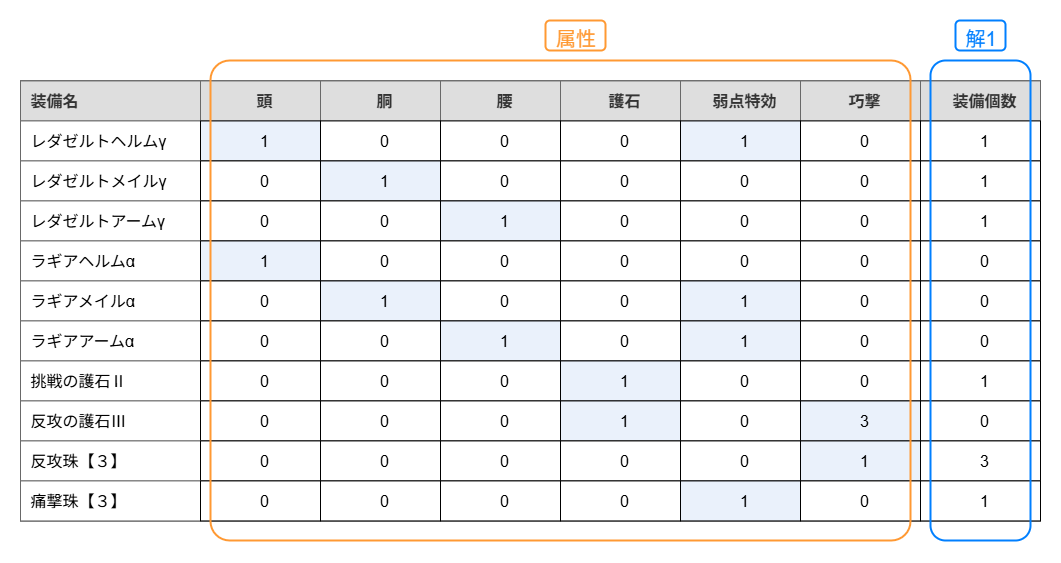
同様にして各装備が持っている装備タイプや付属スキルなどの属性を新しい列として追加すると以下のようなテーブルになります。
弱点特効Lv1がついている装備 レダゼルトヘルムγ や 痛撃珠【3】 には 弱点特効 列に 1 が入力されています。また、巧撃スキルLv3がついている装備 反攻の護石Ⅲ には 巧撃 列に 3 が入力されています。
このテーブルから解1における胴防具の合計数を計算したければ以下のように 胴 列と 解1 列を抽出し、各行の掛け算の結果の合計を計算すればよいです。
また、解1における 弱点特効 スキルの合計レベルを計算したければ 弱点特効 列と 解1 列を抽出し、各行の掛け算の結果の合計を計算すればよいです。
つまり、特定の解におけるある属性の合計値が必要な場合は、対象の属性列と解の列を抽出して、各行の積の和を計算すれば良いことがわかります。
この操作によって以下のような制約条件が全て同じ形式で処理できることがわかります
| 条件の例 | 属性を利用した表現 | 対応する制約条件 |
|---|---|---|
| 胴防具は1個以下しか装備できない |
頭 属性の合計は1以下 |
制約条件(1) |
| 巧撃は最低でもLv3以上必要 |
巧撃 属性の合計は3以上 |
制約条件(2) |
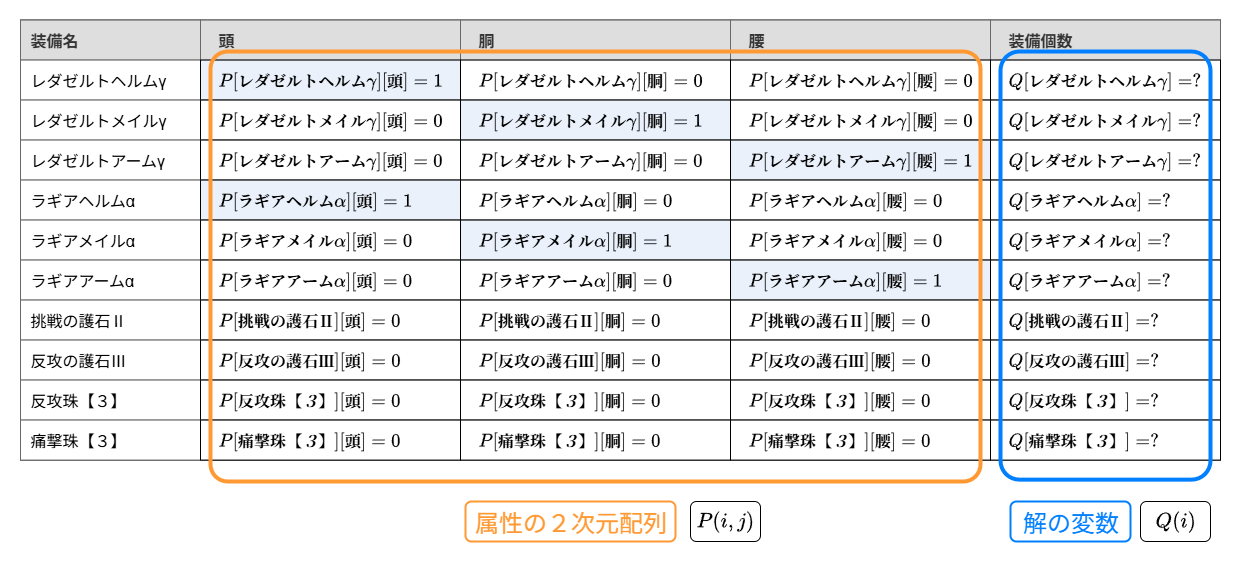
さて、解1は解候補の1つでした。私たちが知りたいのは最適解なので、解の部分を変数 q[i] で表現することにします。さらに、属性部分のテーブルも2次元配列 p[i][j] で表現してみましょう。
テーブルは以下のようになります。
- i は装備名を表しています。
i = レダゼルトヘルムγ, レダゼルトメイルγ, ... 痛撃珠【3】です。 - j は属性を表しています。
j = 頭, 胴, 腰です。
2次元配列のパラメータ p[i][j] と解の変数 q[i] を利用すると制約式 (1) は以下のように書けます。
( p[頭][レダゼルトヘルムγ] * q[レダゼルトヘルムγ]
+ p[頭][レダゼルトメイルγ] * q[レダゼルトメイルγ]
+ ...
+ p[頭][痛撃珠【3】] * q[痛撃珠【3】] ) <= 1
Python っぽく書くと以下のようになります。ジェネレータ式で書くと、前のセクションで出てきた Pyomo の Constraint の実装に近くなってきました。
# for ループで書いた場合
head = 0
for i in ['レダゼルトヘルムγ', 'レダゼルトメイルγ', ... '痛撃珠【3】']:
head += p[i]['頭'] * q[i]
head <= 1
# ジェネレータ式で書いた場合
(p[i]['頭'] * q[i] for i in ['レダゼルトヘルムγ', 'レダゼルトメイルγ', ... '痛撃珠【3】']) <= 1
それでは、上記のジェネレータ式の記法をベースにして制約条件(1)を実装してみましょう。
まずは実装全体を示し、後に各コードの説明をします。以下のように dmax-mini-1.py というファイルに実装しました。実行方法は $ uv run dmax-mini-1.py です。
サンプルコードのリポジトリでは以下から dmax-mini-1.py を確認できます。
# dmax-mini-1.py: 制約条件(1) を実装
from pyomo.environ import *
# =============================================================================
# step1. 入力データ読み込み: 装備データの2次元配列作成、配列のインデックス作成
# =============================================================================
# 全ての装備データ (防具、護石)
equip_all = [
{"type": "head", "name": "レダゼルトヘルムγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "弱点特効": 1, "渾身": 1, "スタミナ急速回復": 1}},
{"type": "torso", "name": "レダゼルトメイルγ", "deffence": 68, "slots": [1, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 3}},
{"type": "arms", "name": "レダゼルトアームγ", "deffence": 68, "slots": [3, 3, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "回避距離UP": 2}},
{"type": "waist", "name": "レダゼルトコイルγ", "deffence": 68, "slots": [0, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 2, "渾身": 2}},
{"type": "legs", "name": "レダゼルトグリーヴγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "スタミナ急速回復": 2, "気絶耐性": 3}},
{"type": "head", "name": "ラギアヘルムα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "渾身": 2, "力の解放": 1, "革細工の柔性": 1}},
{"type": "torso", "name": "ラギアメイルα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "雷耐性": 2, "弱点特効": 1, "スタミナ急速回復": 1, "革細工の柔性": 1}},
{"type": "arms", "name": "ラギアアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"海竜の渦雷": 1, "スタミナ急速回復": 2, "弱点特効": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "waist", "name": "ラギアコイルα", "deffence": 64, "slots": [2, 1, 1], "skills": {"海竜の渦雷": 1, "弱点特効": 1, "渾身": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "legs", "name": "ラギアグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"海竜の渦雷": 1, "弱点特効": 2, "力の解放": 1, "雷耐性": 1, "革細工の柔性": 1}},
{"type": "head", "name": "レギオスヘルムα", "deffence": 64, "slots": [3, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 1, "逆襲": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "torso", "name": "レギオスメイルα", "deffence": 64, "slots": [1, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "逆襲": 1, "鱗張りの技法": 1}},
{"type": "arms", "name": "レギオスアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "回避距離UP": 1, "鱗張りの技法": 1}},
{"type": "waist", "name": "レギオスコイルα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "legs", "name": "レギオスグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "charm", "name": "挑戦の護石Ⅱ", "slots": [0,0,0], "skills": {"挑戦者": 2}},
{"type": "charm", "name": "反攻の護石Ⅲ", "slots": [0,0,0], "skills": {"巧撃": 3}},
]
# 装備の名前集合 (2次元配列 p(i, j) の i の集合)
equip_names = set()
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 装備の全属性の集合 (2次元配列 p(i, j) の j の集合)
attribute_set = set()
attribute_set = attribute_set | single_equip_type_set | {'deffence'}
# 存在するスキルの集合 (後ほど 制約条件(4) の実装で利用)
skill_set = set()
for equip in equip_all:
# 装備名の集合に追加
equip_names.add(equip['name'])
# 属性の集合に追加
for skill in equip['skills']:
attribute_set.add(skill)
skill_set.add(skill)
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
# 装備タイプの属性データを追加
# 例: eqinfo_matrix['レダゼルトヘルムγ', 'head'] = 1
eqinfo_matrix[equip['name'], equip['type']] = 1
# 装備についているスキルの属性データを追加
# 例: eqinfo_matrix['反攻の護石Ⅲ', '巧撃'] = 3
for skill in equip['skills']:
eqinfo_matrix[equip['name'], skill] = equip['skills'][skill]
# 装備の防御力を追加
eqinfo_matrix[equip['name'], 'deffence'] = equip['deffence'] if 'deffence' in equip else 0
# =============================================================================
# step2. モデルの定義: パラメータ、変数、制約条件の追加
# =============================================================================
# モデル定義: 空のモデルを作成
mdl = ConcreteModel(name="dmax model", doc="model for solving damage optimization problem")
# パラメータ定義: 装備データの2次元配列パラメータ
mdl.p = Param(equip_names, attribute_set, default=0, initialize=eqinfo_matrix, within=Integers)
# 変数定義: 各装備を何個使うかを表す変数
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
# =============================================================================
# step3. モデルの出力
# =============================================================================
# モデルの詳細を表示
print(mdl.pprint())
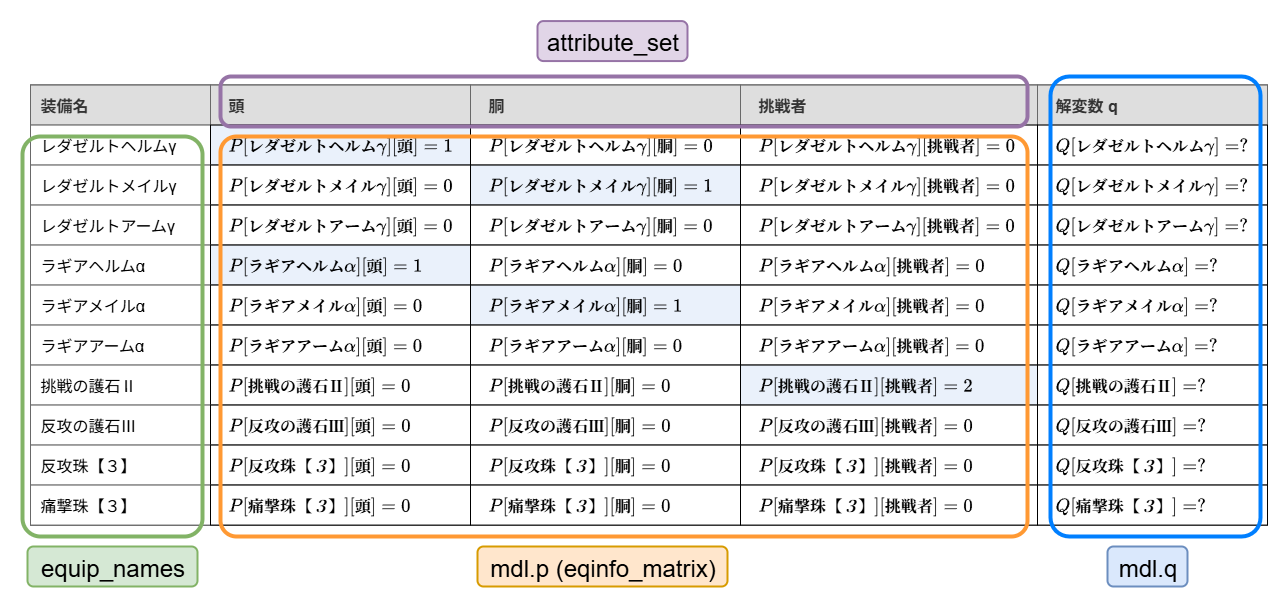
step1 の部分では equip_all という全装備のデータが保存された変数をベースに、3つのデータを準備しています。
| Python 変数名 | 用途 |
|---|---|
equip_all |
全ての装備データが保存された変数この入力データをベースに以下の3つのデータを準備する |
equip_names |
装備名のインデックス (表の縦軸) |
attribute_set |
装備の属性のインデックス (表の横軸) |
eqinfo_matrix |
装備データの2次元配列equip_names と attribute_set で引いて装備データを取得できる |
step2 の部分では空のモデルを作成し、パラメータと変数をモデルに追加しています。
以下の部分では Param クラスを利用し、装備データ2次元配列を mdl.p としてモデルに追加しています。
# 装備データ2次元配列をパラメータとしてモデルに追加
mdl.p = Param(equip_names, attribute_set, default=0, initialize=eqinfo_matrix, within=Integers)
Param クラスの位置引数としては、第1引数に縦軸である装備名インデックス equip_names を指定し、第2引数に装備の属性インデックス attribute_set を指定しています。
Param インスタンスのキーワード引数としては、initialize=eqinfo_matrix により装備データ2次元配列を指定しています。この2次元配列は equip_names と attribute_set で参照できる必要があります。
また、キーワード引数 default=0 を指定しているため、インデックスで eqinfo_matrix を参照した結果が存在しない場合は、0 という値で埋められます。
例えば、eqinfo_matrix['挑戦の護石Ⅱ', 'deffence'] の値は存在しないので、mdl.p('挑戦の護石Ⅱ', 'deffence') = 0 になります。
次に、以下の部分では Var クラスを利用し、解の変数を mdl.q としてモデルに追加しています。インデックスは位置引数 equip_names により装備名のインデックスが指定されています。最適化の完了によってこの変数 mdl.q に最適解が入ります。
# 装備を何個使うかを表す変数をモデルに追加
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
最後に以下の部分で、制約条件(1) をモデルに追加しています。
制約条件(1): 各部位で使用できる装備の数は 1 以下
Constraint クラスでは第1引数にインデックスを指定することによって、インデックスのすべての要素に対して rule= に指定された制約式を定義することができます。
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
今回のケースでは Constraint クラスのインデックスとして single_equip_type_set が指定されているため、1部位しか装備できない装備タイプのすべてについて rule= に指定された制約式を定義しています。
rule= に指定されている関数 const_total_equipment_type(mdl, eqtype) では第2引数として eqtype を受け取っており、ここに single_equip_type_set の各要素が入ります。
つまり、上記の制約式の定義は以下のように部位ごとに定義した場合と同等です。
# 使用できる head の装備の数は 1 以下
def const_total_equipment_type_head(mdl):
return sum(mdl.q[eqname]*mdl.p[eqname, 'head'] for eqname in equip_names) <= 1
mdl.const_total_equipment_type_head = Constraint(rule=const_total_equipment_type_head)
# 使用できる torso の装備の数は 1 以下
def const_total_equipment_type_torso(mdl):
return sum(mdl.q[eqname]*mdl.p[eqname, 'torso'] for eqname in equip_names) <= 1
mdl.const_total_equipment_type_torso = Constraint(rule=const_total_equipment_type_torso)
# arms, waist, legs, charm も同様
それでは実際に実行してモデルの詳細を表示してみましょう。
$ cd ~/dmax-from-scratch-sample-code/
$ uv run dmax-mini-1.py
model for solving damage optimization problem
... 省略
1 Param Declarations のセクションを見ると、コード中でモデルに追加した装備データ2次元配列 mdl.p のデータが入っていることが確認できます。('ラギアアームα', 'arms') : 1 等の表示から、インデックスとそれに対応する値が正しく反映されていることが確認できます。
1 Param Declarations
p : Size=442, Index=p_index, Domain=Integers, Default=0, Mutable=False
Key : Value
('ラギアアームα', 'arms') : 1
('ラギアアームα', 'deffence') : 64
('ラギアアームα', 'スタミナ急速回復') : 2
('ラギアアームα', '弱点特効') : 1
('ラギアアームα', '水場・油泥適応') : 1
('ラギアアームα', '海竜の渦雷') : 1
('ラギアアームα', '革細工の柔性') : 1
... 省略
1 Var Declarations のセクションを見ると、コード中でモデルに追加した解変数 mdl.q のデータが登録されていることがわかります。key の列に装備名が並んでおり、equip_names をインデックスとして定義されていることがわかります。
1 Var Declarations
q : Size=17, Index=q_index
Key : Lower : Value : Upper : Fixed : Stale : Domain
ラギアアームα : 0 : 0 : None : False : False : NonNegativeIntegers
ラギアグリーヴα : 0 : 0 : None : False : False : NonNegativeIntegers
ラギアコイルα : 0 : 0 : None : False : False : NonNegativeIntegers
ラギアヘルムα : 0 : 0 : None : False : False : NonNegativeIntegers
ラギアメイルα : 0 : 0 : None : False : False : NonNegativeIntegers
レギオスアームα : 0 : 0 : None : False : False : NonNegativeIntegers
レギオスグリーヴα : 0 : 0 : None : False : False : NonNegativeIntegers
レギオスコイルα : 0 : 0 : None : False : False : NonNegativeIntegers
レギオスヘルムα : 0 : 0 : None : False : False : NonNegativeIntegers
レギオスメイルα : 0 : 0 : None : False : False : NonNegativeIntegers
レダゼルトアームγ : 0 : 0 : None : False : False : NonNegativeIntegers
レダゼルトグリーヴγ : 0 : 0 : None : False : False : NonNegativeIntegers
レダゼルトコイルγ : 0 : 0 : None : False : False : NonNegativeIntegers
レダゼルトヘルムγ : 0 : 0 : None : False : False : NonNegativeIntegers
レダゼルトメイルγ : 0 : 0 : None : False : False : NonNegativeIntegers
反攻の護石Ⅲ : 0 : 0 : None : False : False : NonNegativeIntegers
挑戦の護石Ⅱ : 0 : 0 : None : False : False : NonNegativeIntegers
1 Constraint Declarations のセクションには制約条件(1)が登録されていることがわかります。
このセクションは興味深いです。Body 列を見ると対応する部位の装備の変数のみが制約式として残っていることが確認できます。例えば key=arms の行では Body= q[レギオスアームα] + q[ラギアアームα] + q[レダゼルトアームγ] となっており、腕防具だけが残されている事がわかります。
1 Constraint Declarations
const_total_equipment_type : Size=6, Index=const_total_equipment_type_index, Active=True
Key : Lower : Body : Upper : Active
arms : -Inf : q[レギオスアームα] + q[ラギアアームα] + q[レダゼルトアームγ] : 1.0 : True
charm : -Inf : q[反攻の護石Ⅲ] + q[挑戦の護石Ⅱ] : 1.0 : True
head : -Inf : q[レダゼルトヘルムγ] + q[ラギアヘルムα] + q[レギオスヘルムα] : 1.0 : True
legs : -Inf : q[レダゼルトグリーヴγ] + q[レギオスグリーヴα] + q[ラギアグリーヴα] : 1.0 : True
torso : -Inf : q[ラギアメイルα] + q[レギオスメイルα] + q[レダゼルトメイルγ] : 1.0 : True
waist : -Inf : q[レギオスコイルα] + q[レダゼルトコイルγ] + q[ラギアコイルα] : 1.0 : True
8 Declarations: p_index_0 p_index_1 p_index p q_index q const_total_equipment_type_index const_total_equipment_type
None
コード中では以下のように、for eqname in equip_names で定義しているため、全ての装備の arms 属性の合計として定義しており、 腕防具ではない防具も含まれています。しかし、モデル定義を表示してみると上記のように腕防具のみの制約式になっています。
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
これはつまり、モデリングツールの時点で既に制約式の最適化が行われているということです。
したがって、コード上でがんばって部位ごとのデータ集合を作成し、部位ごとに制約式の定義を分ける必要はないことがわかります。
💡 小手先の高速化は誤差かもしれない
プログラミングにおける高速化の勘所として「素人が簡単に思いつくようなコード上の最適化や高速化はコンパイラ等によって一瞬で解決されるため、小手先の最適化は誤差かもしれない」というものがあります。なので私も、「コード上で簡単な変数削減などを行っても最適化ソルバーを通せば誤差レベルだろう」という直感がありました。しかし、実際には最適化ソルバーより前の段階で既にモデリングツールによって最適化が行われていて驚きました。
とはいえ、思いついた高速化アイデアの全てがコンパイラなどによって対処されるわけではないので、推測せず計測してみるのが一番です。最適化シミュの高速化を試みるときには、
pprint()メソッドによってモデルの詳細をぜひ確認したいですね。
dmax-mini-1.py の実装状況は以下の通りです。
| 実装完了 | 制約条件 | 制約内容 |
|---|---|---|
| ✅ | 制約条件(1) | 各部位で装備できる個数は1以下 (部位は次の7つ 頭・胴・腕・腰・脚・護石・武器) |
| 制約条件(2) | ユーザが指定したスキルレベルの条件を満たす | |
| 制約条件(3) | 装飾品はスロットレベル以上の大きさのスロットにしか装着できない | |
| 制約条件(4) | ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ | |
| 制約条件(5) | ダメージ計算式において有効なスキルは装備中のスキルのみ | |
| 制約条件(6) | 会心率の上限は100% |
dmax-mini-2.py
さて、この状態ではまだ目的関数を定義していないので、最適化はできません。
次の dmax-mini-2.py では制約式(2)を実装し、さらに目的関数として防御力の合計値を実装してみましょう。これによって簡易的なスキルシミュレーターが完成します。
まずは実装全体を示し、後に dmax-mini-1.py と dmax-mini-2.py の差分コードの説明をします。
dmax-mini-2.py は以下です。実行方法は $ uv run dmax-mini-2.py です。
サンプルコードのリポジトリでは以下から dmax-mini-2.py を確認できます。
# dmax-mini-2.py : 制約条件(1)-(2) を実装
from pyomo.environ import *
# =============================================================================
# step1. 入力データ読み込み: 装備データの2次元配列作成、配列のインデックス作成
# =============================================================================
# 全ての装備データ (防具、護石)
equip_all = [
{"type": "head", "name": "レダゼルトヘルムγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "弱点特効": 1, "渾身": 1, "スタミナ急速回復": 1}},
{"type": "torso", "name": "レダゼルトメイルγ", "deffence": 68, "slots": [1, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 3}},
{"type": "arms", "name": "レダゼルトアームγ", "deffence": 68, "slots": [3, 3, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "回避距離UP": 2}},
{"type": "waist", "name": "レダゼルトコイルγ", "deffence": 68, "slots": [0, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 2, "渾身": 2}},
{"type": "legs", "name": "レダゼルトグリーヴγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "スタミナ急速回復": 2, "気絶耐性": 3}},
{"type": "head", "name": "ラギアヘルムα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "渾身": 2, "力の解放": 1, "革細工の柔性": 1}},
{"type": "torso", "name": "ラギアメイルα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "雷耐性": 2, "弱点特効": 1, "スタミナ急速回復": 1, "革細工の柔性": 1}},
{"type": "arms", "name": "ラギアアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"海竜の渦雷": 1, "スタミナ急速回復": 2, "弱点特効": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "waist", "name": "ラギアコイルα", "deffence": 64, "slots": [2, 1, 1], "skills": {"海竜の渦雷": 1, "弱点特効": 1, "渾身": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "legs", "name": "ラギアグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"海竜の渦雷": 1, "弱点特効": 2, "力の解放": 1, "雷耐性": 1, "革細工の柔性": 1}},
{"type": "head", "name": "レギオスヘルムα", "deffence": 64, "slots": [3, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 1, "逆襲": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "torso", "name": "レギオスメイルα", "deffence": 64, "slots": [1, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "逆襲": 1, "鱗張りの技法": 1}},
{"type": "arms", "name": "レギオスアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "回避距離UP": 1, "鱗張りの技法": 1}},
{"type": "waist", "name": "レギオスコイルα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "legs", "name": "レギオスグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "charm", "name": "挑戦の護石Ⅱ", "slots": [0,0,0], "skills": {"挑戦者": 2}},
{"type": "charm", "name": "反攻の護石Ⅲ", "slots": [0,0,0], "skills": {"巧撃": 3}},
]
# 装備の名前集合 (2次元配列 p(i, j) の i の集合)
equip_names = set()
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 装備の全属性の集合 (2次元配列 p(i, j) の j の集合)
attribute_set = set()
attribute_set = attribute_set | single_equip_type_set | {'deffence'}
# 存在するスキルの集合 (後ほど 制約条件(4) の実装で利用)
skill_set = set()
for equip in equip_all:
# 装備名の集合に追加
equip_names.add(equip['name'])
# 属性の集合に追加
for skill in equip['skills']:
attribute_set.add(skill)
skill_set.add(skill)
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
# 装備タイプの属性データを追加
# 例: eqinfo_matrix['レダゼルトヘルムγ', 'head'] = 1
eqinfo_matrix[equip['name'], equip['type']] = 1
# 装備についているスキルの属性データを追加
# 例: eqinfo_matrix['反攻の護石Ⅲ', '巧撃'] = 3
for skill in equip['skills']:
eqinfo_matrix[equip['name'], skill] = equip['skills'][skill]
# 装備の防御力を追加
eqinfo_matrix[equip['name'], 'deffence'] = equip['deffence'] if 'deffence' in equip else 0
# ユーザが指定する必須スキルレベルのデータ
required_skills = {
"逆襲": 2,
"巧撃": 0,
"挑戦者": 0,
"弱点特効": 0,
"渾身": 0,
"力の解放": 0,
"煌雷竜の力": 0,
"ヌシの魂": 0,
"海竜の渦雷": 0,
"千刃竜の闘志": 0,
"スタミナ急速回復": 0,
"回避距離UP": 0,
"気絶耐性": 0,
"革細工の柔性": 0,
"雷耐性": 0,
"水場・油泥適応": 0,
"裂傷耐性": 0,
"鱗張りの技法": 0,
"回避性能": 0,
}
# =============================================================================
# step2. モデルの定義: パラメータ、変数、制約条件、目的関数の追加
# =============================================================================
# モデル定義: 空のモデルを作成
mdl = ConcreteModel(name="dmax model", doc="model for solving damage optimization problem")
# パラメータ定義: 装備データの2次元配列パラメータ
mdl.p = Param(equip_names, attribute_set, default=0, initialize=eqinfo_matrix, within=Integers)
# 変数定義: 各装備を何個使うかを表す変数
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
# パラメータ定義: ユーザが指定した必須スキルレベル
mdl.r = Param(required_skills.keys(), default=0, initialize=required_skills, within=Integers)
# 制約条件(2): ユーザが指定したスキルレベルの条件を満たす
def const_skill_point(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname,skill] for eqname in equip_names) >= mdl.r[skill]
mdl.const_skill_point = Constraint(required_skills.keys(), rule=const_skill_point)
# 目的関数: 防御力の合計を最大化
def objective(mdl):
return sum(mdl.q[eqname] * mdl.p[eqname, 'deffence'] for eqname in equip_names)
mdl.OBJ = Objective(rule=objective, sense=maximize)
# =============================================================================
# step3. モデルの出力
# =============================================================================
# モデルの詳細を表示
print(mdl.pprint())
# 問題ファイルを出力
import os
output_filename = f"{os.path.splitext(os.path.basename(__file__))[0]}-problem.nl"
mdl.write(output_filename, format="nl", io_options={'symbolic_solver_labels': True})
dmax-mini-1.py と dmax-mini-2.py の差分コードの説明をします。
以下の dict 変数 required_skills はスキルレベルの下限を設定しています。
スキルシミュレーターでユーザーが必須スキルのレベルを指定する部分に相当します。
実際のアプリケーションとして提供する際にはこのようにハードコードするのではなく、UI等からユーザが入力できるように実装する必要があります。
required_skills = {
"逆襲": 2,
"巧撃": 0,
"挑戦者": 0,
# 省略
}
以下の部分では、まずユーザが指定した必須スキルレベルのデータ required_skills をパラメータ mdl.r としてモデルに追加しています。
mdl.r の定義においてもインデックスとして required_skills.keys() を指定することで一括でパラメータを追加しています。
さらに関数 const_skill_point() の部分では以下のような形で制約条件(2)に相当する式を定義しています。
(使用する全ての装備の
skill属性の合計) >= (ユーザが指定したskillの下限レベル)
# ユーザが指定した必須スキルレベルをパラメータとしてモデルに追加
mdl.r = Param(required_skills.keys(), default=0, initialize=required_skills, within=Integers)
# 制約条件(2): ユーザが指定したスキルレベルの条件を満たす
def const_skill_point(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname,skill] for eqname in equip_names) >= mdl.r[skill]
mdl.const_skill_point = Constraint(required_skills.keys(), rule=const_skill_point)
以下の部分では目的関数として防御力の合計値を設定し、最大化する方針でモデルに追加しています。
(使用する全ての装備の
deffence属性の合計)
# 目的関数: 防御力の合計を最大化
def objective(mdl):
return sum(mdl.q[eqname] * mdl.p[eqname, 'deffence'] for eqname in equip_names)
mdl.OBJ = Objective(rule=objective, sense=maximize)
今回は防御力の合計を最大化するように指定しましたが、防御力の最小化でもスキルシミュレーターとしては機能しますし、別の属性をターゲットにしても構いません。最適化シミュレーターとして動作させる以上、目的関数が必要なのでとりあえず有用で簡単そうな防御力の合計を指定しただけです。
他の有用そうな目的関数としては例えば装飾品の空きスロット数などが良さそうです。最終的にはこの目的関数をダメージ計算式に置き換えることでダメージ最大化シミューレータを実装します。
最後に、以下の部分で問題ファイルを出力しています。
問題ファイル名はプログラムのファイル名をベースにしており、ファイル名 dmax-mini-2.py の場合は、問題ファイル dmax-mini-2-problem.nl というファイル名前のファイルが出力されます。
このファイルを SCIP ソルバーに入力することで最適解が得られます。
# 問題ファイルを出力
import os
output_filename = f"{os.path.splitext(os.path.basename(__file__))[0]}-problem.nl"
mdl.write(output_filename, format="nl", io_options={'symbolic_solver_labels': True})
dmax-mini-1.py からの差分は以上です。
それでは dmax-mini-2.py を実行して問題ファイルを出力し、SCIP ソルバーに最適化させてみましょう。
dmax-mini-2.py を実行するとまず、mdl.pprint() によってモデル詳細が出力されます。
出力内容から、パラメータ mdl.r、目的関数 mdl.OBJ、そして制約条件 mdl.const_skill_point が追加されていることが確認できます。dmax-mini-1.py のときと同様に mdl.const_skill_point の制約式においても関係のある装備だけが抽出されていることがわかります。
$ cd ~/dmax-from-scratch-sample-code/
$ uv run dmax-mini-2.py
model for solving damage optimization problem
...省略
2 Param Declarations
...省略
r : Size=19, Index=r_index, Domain=Integers, Default=0, Mutable=False
Key : Value
スタミナ急速回復 : 0
ヌシの魂 : 0
...省略
1 Objective Declarations
OBJ : Size=1, Index=None, Active=True
Key : Active : Sense : Expression
None : True : maximize : 64*q[ラギアヘルムα] + 64*q[レギオスヘルムα] + 68*q[レダゼルトヘルムγ] + 64*q[レギオスコイルα] + 64*q[ラギアメイルα] + 64*q[ラギアアームα] + 64*q[ラギアグリーヴα] + 64*q[ラギアコイルα] + 68*q[レダゼルトアームγ] + 64*q[レギオスグリーヴα] + 68*q[レダゼルトコイルγ] + 68*q[レダゼルトグリーヴγ] + 68*q[レダゼルトメイルγ] + 64*q[レギオスメイルα] + 64*q[レギオスアームα]
2 Constraint Declarations
const_skill_point : Size=19, Index=const_skill_point_index, Active=True
Key : Lower : Body : Upper : Active
スタミナ急速回復 : 0.0 : q[レダゼルトヘルムγ] + q[ラギアメイルα] + 2*q[ラギアアームα] + 2*q[レダゼルトグリーヴγ] : +Inf : True
ヌシの魂 : 0.0 : q[レダゼルトヘルムγ] + q[レダゼルトアームγ] + q[レダゼルトコイルγ] + q[レダゼルトグリーヴγ] + q[レダゼルトメイルγ] : +Inf : True
...省略
また、mdl.write() によって問題ファイル dmax-mini-2-problem.nl が出力されていることも確認できます。
$ ls -lh | grep dmax-mini-2-prob
-rw-r--r-- 1 hoge hoge 458 Aug 4 21:30 dmax-mini-2-problem.col
-rw-r--r-- 1 hoge hoge 2.6K Aug 4 21:30 dmax-mini-2-problem.nl
-rw-r--r-- 1 hoge hoge 840 Aug 4 21:30 dmax-mini-2-problem.row
上記の問題ファイルをSCIPソルバーに入力して最適化しましょう。
以下のようにSCIPソルバーを起動し、コマンドを実行します。
# 問題ファイルが存在するディレクトリに移動
$ cd ~/dmax-from-scratch-sample-code/
# scip 対話モードを起動 (rscip エイリアスについては環境構築のセクションを参照)
$ rscip
# read コマンドで問題ファイルを読み込み
SCIP> read dmax-mini-2-problem.nl
# optimize コマンドで最適化
SCIP> optimize
# display solution コマンドで最適化の結果を表示
SCIP> display solution
実行結果は以下のようになりました。
required_skills において 逆襲Lv2 を指定しているため、レギオスヘルムα (逆襲Lv1) と レギオスメイルα (逆襲Lv1) が採用されていることが分かります。
$ rscip
SCIP> read dmax-mini-2-problem.nl
...省略
SCIP> optimize
...省略
SCIP Status : problem is solved [optimal solution found]
Solving Time (sec) : 0.00
Solving Nodes : 0
Primal Bound : +3.32000000000000e+02 (1 solutions)
Dual Bound : +3.32000000000000e+02
Gap : 0.00 %
SCIP> display solution
objective value: 332
q[レギオスヘルムα] 1 (obj:64)
q[レギオスメイルα] 1 (obj:64)
q[レダゼルトアームγ] 1 (obj:68)
q[レダゼルトグリーヴγ] 1 (obj:68)
q[レダゼルトコイルγ] 1 (obj:68)
q[反攻の護石Ⅲ] 1 (obj:0)
SCIP>
装備データを確認すると、他に逆襲スキルが付いた防具はありません。したがって、required_skills において 逆襲Lv3 を指定すれば装備が組めなくなるはずです。
ぜひ required_skills を修正して再実行して試してみてください。
以下のように SCIP Status が infeasible となり、指定された条件は実現不可能であるという結果が返ってくるはずです。
SCIP> optimize
...省略
SCIP Status : problem is solved [infeasible]
...省略
dmax-mini-2.py の実装状況は以下の通りです。
dmax-mini-2.py では制約条件(1), (2)に加えて目的関数を追加したことにより、簡易的なスキルシミュレーターが完成しました。
| 実装完了 | 制約条件 | 制約内容 |
|---|---|---|
| ✅ | 制約条件(1) | 各部位で装備できる個数は1以下 (部位は次の7つ 頭・胴・腕・腰・脚・護石・武器) |
| ✅ | 制約条件(2) | ユーザが指定したスキルレベルの条件を満たす |
| 制約条件(3) | 装飾品はスロットレベル以上の大きさのスロットにしか装着できない | |
| 制約条件(4) | ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ | |
| 制約条件(5) | ダメージ計算式において有効なスキルは装備中のスキルのみ | |
| 制約条件(6) | 会心率の上限は100% |
dmax-mini-3.py
dmax-mini-2.py では装飾品を考慮していません。
dmax-mini-3.py では制約条件(3)を実装して装飾品を扱えるようにしましょう。ここまで実装すればスキルシミュレーターが完成します!
装飾品の条件については必要な実装自体は少ないのですが、制約式に落とし込む部分で一捻り必要です。
まずは制約条件(3)の定式化から説明します。
制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
制約条件(3)をいきなり式に落とし込むのは難しいです。
難しい理由は、よりレベルの高いスロットにも装着できる という性質があるからです。
例えば、Lv2装飾品はLv2スロに装着できるだけでなくLv3スロにも装着できるという性質があります。
なのでまずは、条件を簡単にするためにこの性質がない場合を考えてみましょう。
つまり、
制約条件(3A): 装飾品は同じレベルのスロットにしか装着できない
という条件になります。
簡単のために最初は Lv1 と Lv2 だけを考慮して定式化するとは以下のような制約式になります。
\begin{array}{cc}
(\text{装備中のLv1スロットの数}) \geq (\text{装備中のLv1装飾品の数}) \\
(\text{装備中のLv2スロットの数}) \geq (\text{装備中のLv2装飾品の数}) \\
\end{array}
例えばLv1の場合、装備しているLv1装飾品の数が、装備している防具に付属しているLv1スロットの数以下に収まれば良い という条件になっています。使用できるスロットはLv1スロットの枠だけであり、仮にLv2スロットやLv3スロットの枠が余っていてもLv1装飾品は装着できない条件となっていることがわかります。
横幅を短くするため (装備中のLv1スロットの数) 等を省略して (Lv1スロ数) 等と表記することにします。
\begin{array}{cc}
(\text{Lv1スロ数}) \geq (\text{Lv1装飾品数}) \\
(\text{Lv2スロ数}) \geq (\text{Lv2装飾品数}) \\
\end{array}
制約条件(3A) を図示すると以下のようになります。Lv2スロット群とLv1スロット群の間には壁があり、Lv2スロットの領域とLv1スロットの領域が別れている状態です。
装着パターン1 のように、Lv2装飾品とLv1装飾品はそれぞれ左右の両端から同じレベルのスロット枠を消費していくと考えます。
装着パターン2 のように、同じレベルのスロットを消費しきってしまった後はそれ以上装飾品をつけることはできません。
Lv2装飾品はLv1スロットの領域に侵食してLv1スロットに装着することはできませんし、Lv1装飾品もLv2スロットの領域に対して侵食できません。
お互いに不可侵の状態になっていると言えます。
さて、制約条件(3A)は実際のゲームの条件に比べて、より高いレベルのスロットに装着できない という点が厳しすぎました。次はこの点を解消して よりレベルの高いスロットにも装着できる という性質を追加したいです。
この よりレベルの高いスロットにも装着できる という性質には より大きいスロットには装着できるが、より小さいスロットには装着できない という非対称性があります。
簡単のために一旦この非対称性を無視して対称性のある条件を考えると以下のような条件になります。
制約条件(3B): 装飾品はどのレベルのスロットにも装着できる
この場合、Lv1装飾品をLv2スロットに装着できるだけでなく、Lv2装飾品もLv1スロットに装着できるようになります。今度は逆に制限を緩め過ぎなので後ほど修正する必要がありますが、一旦この対称的な制約条件(3B)で考えてみます。
制約条件(3B)を数式と図で表すと以下のようになります。
(\text{Lv2スロ数}) + (\text{Lv1スロ数}) \geq (\text{Lv2装飾品数}) + (\text{Lv1装飾品数})
制約条件(3A)にあったLv2スロット領域とLv1スロット領域を分断する壁がなくなりました。
Lv2装飾品はLv1スロットの領域に侵食してLv1スロットにも装着できますし、逆も同様に侵食できます。
さて、実際のゲームに照らし合わせると、侵食方向のうちLv1装飾品がLv2スロット領域に侵食する方向は正しいですが、Lv2装飾品がLv1スロット領域に侵食する方向は間違っています。なので、現状の制約条件から Lv2装飾品がLv1スロット領域に侵食する方向 のみ禁止して、非対称性を再現したいです。
Lv2装飾品の侵食範囲の限界は装備中のLv2スロットの数です。したがって以下のような式を追加する必要があります。
(\text{Lv2スロ数}) \geq (\text{Lv2装飾品数})
制約条件(3B) と合わせて考えると以下のようになります。
\begin{array}{lcl}
(\text{Lv2スロ数}) + (\text{Lv1スロ数}) & \geq & (\text{Lv2装飾品数}) + (\text{Lv1装飾品数}) \\
(\text{Lv2スロ数}) & \geq & (\text{Lv2装飾品数})
\end{array}
次はLv3装飾品も考慮に入れましょう。
制約条件(3B): 装飾品はどのレベルのスロットにも装着できる
についてLv3も考慮に入れた式は以下のようになります。
\begin{array}{lcl}
(\text{Lv3スロ数}) + (\text{Lv2スロ数}) + (\text{Lv1スロ数}) & \geq & (\text{Lv3装飾品数}) + (\text{Lv2装飾品数}) + (\text{Lv1装飾品数})
\end{array}
ここから侵食範囲の限界を設定していきましょう。
まず、Lv3装飾品がLv2以下のスロット領域に侵食する方向 を禁止したいです。Lv3装飾品の侵食範囲の限界はLv3スロットの数です。
したがって以下のようになります。
\begin{array}{lcl}
(\text{Lv3スロ数}) + (\text{Lv2スロ数}) + (\text{Lv1スロ数}) & \geq & (\text{Lv3装飾品数}) + (\text{Lv2装飾品数}) + (\text{Lv1装飾品数}) \\
(\text{Lv3スロ数}) & \geq & (\text{Lv3装飾品数})
\end{array}
さらに、Lv3装飾品とLv2装飾品がLv1以下のスロット領域に侵食する方向 も禁止したいです。
Lv3装飾品とLv2装飾品の侵食範囲の限界はLv3スロットとLv2スロットの数の合計なので (Lv3スロ数}) + (Lv2スロ数}) となります。
したがって以下のようになります。
\begin{array}{lcl}
(\text{Lv3スロ数}) + (\text{Lv2スロ数}) + (\text{Lv1スロ数}) & \geq & (\text{Lv3装飾品数}) + (\text{Lv2装飾品数}) + (\text{Lv1装飾品数}) \\
(\text{Lv3スロ数}) + (\text{Lv2スロ数}) & \geq & (\text{Lv3装飾品数}) + (\text{Lv2装飾品数}) \\
(\text{Lv3スロ数}) & \geq & (\text{Lv3装飾品数})
\end{array}
結果的に制約条件(3)は以下の式にまとめられます。
制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
\begin{array}{lcl}
(\text{Lv1以上のスロ数}) & \geq & (\text{Lv1以上の装飾品数}) \\
(\text{Lv2以上のスロ数}) & \geq & (\text{Lv2以上の装飾品数}) \\
(\text{Lv3以上のスロ数}) & \geq & (\text{Lv3以上の装飾品数})
\end{array}
実装を楽にするために、以下のように移項しておきましょう。
右辺が0になりループ処理が左辺のみになります。
\begin{array}{lcl}
(\text{Lv1以上のスロ数}) - (\text{Lv1以上の装飾品数}) & \geq & 0 \\
(\text{Lv2以上のスロ数}) - (\text{Lv2以上の装飾品数}) & \geq & 0 \\
(\text{Lv3以上のスロ数}) - (\text{Lv3以上の装飾品数}) & \geq & 0
\end{array}
Lv1以上のスロ数 は ある解 q[i] において使用する装備に付属しているLv1以上の装飾品スロット数の合計 を示しています。
Lv1以上の装飾品数 も同様に、ある解 q[i] において使用するLv1以上の装飾品の合計数 を示しています。
例えば、ある解 q[i] がもし以下のような装備の組み合わせだった場合、(Lv1以上のスロ数) = 8 であり、(Lv1以上の装飾品数) = 3 です。
| 部位 | 装備名 | スロット |
|---|---|---|
| 頭 | ラギアヘルムα | 2-1-0 |
| 胴 | ラギアメイルα | 2-1-0 |
| 腕 | ラギアアームα | 2-0-0 |
| 腰 | ラギアコイルα | 2-1-1 |
| 脚 | レギオスグリーヴα | 0-0-0 |
| 護石 | 反攻の護石Ⅲ | 0-0-0 |
| 装飾品 | 逆襲珠【2】 | 2 |
| 装飾品 | 逆襲珠【2】 | 2 |
| 装飾品 | 体術珠【1】 | 1 |
ここで、Lv1以上のスロ数 と Lv1以上の装飾品数 をまとめて新しい属性 Lv123RemainSlotNum (Lv1以上のスロットの余り数) として扱うことにします。
同様に Lv2以上のスロットの余り数を属性 Lv23RemainSlotNum、Lv3以上のスロットの余り数を属性 Lv3RemainSlotNum として扱うことにします。
- スロットが (2-1-0) の装備の場合、
(Lv123RemainSlotNum) = 2、(Lv23RemainSlotNum) = 1となります。 - Lv1の装飾品の場合は、Lv1以上のスロットの余り数を消費すると考え、
(Lv123RemainSlotNum) = -2となります。
このように考えると、最終的に以下のような式にまとめられます。
\begin{array}{lcl}
(\text{装備中の Lv123RemainSlotNum の合計}) & \geq & 0 \\
(\text{装備中の Lv23RemainSlotNum の合計}) & \geq & 0 \\
(\text{装備中の Lv3RemainSlotNum の合計}) & \geq & 0
\end{array}
それでは立式した制約条件(3)を dmax-mini-3.py に実装していきましょう。
まずは装飾品データを equip_all 変数に追加します。
モンハンワイルズには防具装飾品と武器装飾品がありますが、どちらも処理は同じなので今回は防具装飾品のみ実装しましょう。
防具装飾品の type は decoArmor としています。
# 全ての装備データ (防具、護石、装飾品)
equip_all = [
...省略
{"type": "charm", "name": "挑戦の護石Ⅱ", "slots": [0,0,0], "skills": {"挑戦者": 2}},
{"type": "charm", "name": "反攻の護石Ⅲ", "slots": [0,0,0], "skills": {"巧撃": 3}},
+ {"type": "decoArmor", "name": "反攻珠【3】", "size": 3, "skills": {"巧撃": 1}},
+ {"type": "decoArmor", "name": "逆襲珠【2】", "size": 2, "skills": {"逆襲": 1}},
+ {"type": "decoArmor", "name": "痛撃珠【3】", "size": 3, "skills": {"弱点特効": 1}},
+ {"type": "decoArmor", "name": "渾身珠【2】", "size": 2, "skills": {"渾身": 1}},
+ {"type": "decoArmor", "name": "体術珠【1】", "size": 1, "skills": {"体術": 1}},
+ {"type": "decoArmor", "name": "早気珠【2】", "size": 2, "skills": {"スタミナ急速回復": 1}},
+ {"type": "decoArmor", "name": "挑戦珠【3】", "size": 3, "skills": {"挑戦者": 1}},
+ {"type": "decoArmor", "name": "全開珠【3】", "size": 3, "skills": {"力の解放": 1}},
]
次に、スロットの余り数属性 Lv123RemainSlotNum, Lv23RemainSlotNum, Lv3RemainSlotNum を実装します。以下のように attribute_set に追加することで、スロットの余り数属性をインデックスとして準備できます。
+# 装飾品スロットの属性
+remain_slot_set = {'Lv123RemainSlotNum', 'Lv23RemainSlotNum', 'Lv3RemainSlotNum'}
# 装備の全属性の集合 (2次元配列 p(i, j) の j の集合)
attribute_set = set()
-attribute_set = attribute_set | single_equip_type_set | {'deffence'}
+attribute_set = attribute_set | single_equip_type_set | {'deffence'} | {'decoArmor'} | remain_slot_set
次は装飾品のスロットレベルデータ "size" を利用して、 Lv123RemainSlotNum 等の余りスロット数属性に対応するデータを作成し、装備データの2次元配列 eqinfo_matrix に登録します。
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
... 省略
# 装備の防御力を追加
eqinfo_matrix[equip['name'], 'deffence'] = equip['deffence'] if 'deffence' in equip else 0
+ # 装飾品の残りスロット属性を追加
+ if equip['type'] == 'decoArmor':
+ eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = -1 if equip['size'] >= 1 else 0
+ eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = -1 if equip['size'] >= 2 else 0
+ eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = -1 if equip['size'] >= 3 else 0
以下の部分は三項演算子を利用しています。equip['size'] >= 1 が成立するなら -1 を返し、成立しないなら 0 を返します。
-1 if equip['size'] >= 1 else 0
C系列の三項演算子になれていると Python の三項演算子は読みづらいかもしれません。
C言語などにおける (a > b) ? a : b を Python で書くと a if (a > b) else b になります。
💡 三項演算子の可読性
「そもそも三項演算子が読みづらい」という指摘があるかもしれませんが、上記のように三項演算子を利用して上下を並べて書ける場合には同じ処理の繰り返しであることがわかりやすく、コンパクトで可読性の高い書き方ができると思います。
同じ処理なのでループで書く案もありますが、既に for ループの内部なのでネストが深くなり可読性が下がってしまうと思います。3つ程度の要素数であればループで書くとむしろ可読性が下がるとも思います。三項演算子の部分を関数として切り出すのは良いと思います。ただ個人的には関数を次々に追いかける玉ねぎの皮むきみたいなコードリーディングはあまり好きではないので採用しませんでした。
次は、装飾品以外の装備の余りスロット数属性を追加します。
装備には複数のスロットがあるため、各スロットを全てチェックして Lv123RemainSlotNum などの余りスロット数属性のデータを追加していきます。
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
...省略
# 装飾品の残りスロット属性を追加
if equip['type'] == 'decoArmor':
eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = -1 if equip['size'] >= 1 else 0
eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = -1 if equip['size'] >= 2 else 0
eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = -1 if equip['size'] >= 3 else 0
+ # 装備の残りスロット属性を追加
+ if equip['type'] in single_equip_type_set:
+ eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = len(list(filter(lambda n: n >= 1, equip['slots'])))
+ eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = len(list(filter(lambda n: n >= 2, equip['slots'])))
+ eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = len(list(filter(lambda n: n >= 3, equip['slots'])))
filter(lambda n: n >= 1, equip['slots']) の部分では対象の装備のスロット配列 equip['slots'] のうちレベル1以上の要素のみを抽出しています。
len(list(filter(lambda n: n >= 3, equip['slots']))) の部分ではレベル1以上のスロット数を計算し、Lv123RemainSlotNum に対応するデータとして登録しています。
慣れればコンパクトに認識できて良いですが、さすがにこれは関数に切り出すべきだったかもしれません。
最後に制約条件(3)を実装しモデルに追加します。
これまでと同様に、余りスロット数属性の集合 remain_slot_set の各要素について、以下の制約式を定義しています。
\begin{array}{lcl}
(\text{装備中の Lv123RemainSlotNum の合計}) & \geq & 0 \\
(\text{装備中の Lv23RemainSlotNum の合計}) & \geq & 0 \\
(\text{装備中の Lv3RemainSlotNum の合計}) & \geq & 0
\end{array}
# 装飾品スロットの属性
remain_slot_set = {'Lv123RemainSlotNum', 'Lv23RemainSlotNum', 'Lv3RemainSlotNum'}
# 制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
def const_remain_slot_num_armor(mdl, slotlevel):
return sum(mdl.q[eqname]*mdl.p[eqname,slotlevel] for eqname in equip_names) >= 0
mdl.const_remain_slot_num_armor = Constraint(remain_slot_set, rule=const_remain_slot_num_armor)
以上で dmax-mini-3.py の実装は終了です。dmax-mini-3.py のファイル全体を以下に示します。
サンプルコードのリポジトリでは以下から dmax-mini-3.py を確認できます。
# dmax-mini-3.py: 制約条件(1)-(3) を実装
from pyomo.environ import *
# =============================================================================
# step1. 入力データ読み込み: 装備データの2次元配列作成、配列のインデックス作成
# =============================================================================
# 全ての装備データ (防具、護石、装飾品)
equip_all = [
{"type": "head", "name": "レダゼルトヘルムγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "弱点特効": 1, "渾身": 1, "スタミナ急速回復": 1}},
{"type": "torso", "name": "レダゼルトメイルγ", "deffence": 68, "slots": [1, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 3}},
{"type": "arms", "name": "レダゼルトアームγ", "deffence": 68, "slots": [3, 3, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "回避距離UP": 2}},
{"type": "waist", "name": "レダゼルトコイルγ", "deffence": 68, "slots": [0, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 2, "渾身": 2}},
{"type": "legs", "name": "レダゼルトグリーヴγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "スタミナ急速回復": 2, "気絶耐性": 3}},
{"type": "head", "name": "ラギアヘルムα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "渾身": 2, "力の解放": 1, "革細工の柔性": 1}},
{"type": "torso", "name": "ラギアメイルα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "雷耐性": 2, "弱点特効": 1, "スタミナ急速回復": 1, "革細工の柔性": 1}},
{"type": "arms", "name": "ラギアアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"海竜の渦雷": 1, "スタミナ急速回復": 2, "弱点特効": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "waist", "name": "ラギアコイルα", "deffence": 64, "slots": [2, 1, 1], "skills": {"海竜の渦雷": 1, "弱点特効": 1, "渾身": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "legs", "name": "ラギアグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"海竜の渦雷": 1, "弱点特効": 2, "力の解放": 1, "雷耐性": 1, "革細工の柔性": 1}},
{"type": "head", "name": "レギオスヘルムα", "deffence": 64, "slots": [3, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 1, "逆襲": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "torso", "name": "レギオスメイルα", "deffence": 64, "slots": [1, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "逆襲": 1, "鱗張りの技法": 1}},
{"type": "arms", "name": "レギオスアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "回避距離UP": 1, "鱗張りの技法": 1}},
{"type": "waist", "name": "レギオスコイルα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "legs", "name": "レギオスグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "charm", "name": "挑戦の護石Ⅱ", "slots": [0,0,0], "skills": {"挑戦者": 2}},
{"type": "charm", "name": "反攻の護石Ⅲ", "slots": [0,0,0], "skills": {"巧撃": 3}},
{"type": "decoArmor", "name": "反攻珠【3】", "size": 3, "skills": {"巧撃": 1}},
{"type": "decoArmor", "name": "逆襲珠【2】", "size": 2, "skills": {"逆襲": 1}},
{"type": "decoArmor", "name": "痛撃珠【3】", "size": 3, "skills": {"弱点特効": 1}},
{"type": "decoArmor", "name": "渾身珠【2】", "size": 2, "skills": {"渾身": 1}},
{"type": "decoArmor", "name": "体術珠【1】", "size": 1, "skills": {"体術": 1}},
{"type": "decoArmor", "name": "早気珠【2】", "size": 2, "skills": {"スタミナ急速回復": 1}},
{"type": "decoArmor", "name": "挑戦珠【3】", "size": 3, "skills": {"挑戦者": 1}},
{"type": "decoArmor", "name": "全開珠【3】", "size": 3, "skills": {"力の解放": 1}},
]
# 装備の名前集合 (2次元配列 p(i, j) の i の集合)
equip_names = set()
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 装飾品スロットの属性
remain_slot_set = {'Lv123RemainSlotNum', 'Lv23RemainSlotNum', 'Lv3RemainSlotNum'}
# 装備の全属性の集合 (2次元配列 p(i, j) の j の集合)
attribute_set = set()
attribute_set = attribute_set | single_equip_type_set | {'deffence'} | {'decoArmor'} | remain_slot_set
# 存在するスキルの集合 (後ほど 制約条件(4) の実装で利用)
skill_set = set()
for equip in equip_all:
# 装備名の集合に追加
equip_names.add(equip['name'])
# 属性の集合に追加
for skill in equip['skills']:
attribute_set.add(skill)
skill_set.add(skill)
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
# 装備タイプの属性データを追加
# 例: eqinfo_matrix['レダゼルトヘルムγ', 'head'] = 1
eqinfo_matrix[equip['name'], equip['type']] = 1
# 装備についているスキルの属性データを追加
# 例: eqinfo_matrix['反攻の護石Ⅲ', '巧撃'] = 3
for skill in equip['skills']:
eqinfo_matrix[equip['name'], skill] = equip['skills'][skill]
# 装備の防御力を追加
eqinfo_matrix[equip['name'], 'deffence'] = equip['deffence'] if 'deffence' in equip else 0
# 装飾品の残りスロット属性を追加
if equip['type'] == 'decoArmor':
eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = -1 if equip['size'] >= 1 else 0
eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = -1 if equip['size'] >= 2 else 0
eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = -1 if equip['size'] >= 3 else 0
# 装備の残りスロット属性を追加
if equip['type'] in single_equip_type_set:
eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = len(list(filter(lambda n: n >= 1, equip['slots'])))
eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = len(list(filter(lambda n: n >= 2, equip['slots'])))
eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = len(list(filter(lambda n: n >= 3, equip['slots'])))
# ユーザが指定する必須スキルレベルのデータ
required_skills = {
"巧撃": 5,
"挑戦者": 0,
"逆襲": 3,
"弱点特効": 5,
"渾身": 0,
"力の解放": 0,
"煌雷竜の力": 0,
"ヌシの魂": 0,
"海竜の渦雷": 0,
"千刃竜の闘志": 0,
"スタミナ急速回復": 3,
"体術": 4,
"回避距離UP": 0,
"気絶耐性": 0,
"革細工の柔性": 0,
"雷耐性": 0,
"水場・油泥適応": 0,
"裂傷耐性": 0,
"鱗張りの技法": 0,
"回避性能": 0,
}
# =============================================================================
# step2. モデルの定義: パラメータ、変数、制約条件、目的関数の追加
# =============================================================================
# モデル定義: 空のモデルを作成
mdl = ConcreteModel(name="dmax model", doc="model for solving damage optimization problem")
# パラメータ定義: 装備データの2次元配列パラメータ
mdl.p = Param(equip_names, attribute_set, default=0, initialize=eqinfo_matrix, within=Integers)
# 変数定義: 各装備を何個使うかを表す変数
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
# パラメータ定義: ユーザが指定した必須スキルレベル
mdl.r = Param(required_skills.keys(), default=0, initialize=required_skills, within=Integers)
# 制約条件(2): ユーザが指定したスキルレベルの条件を満たす
def const_skill_point(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname,skill] for eqname in equip_names) >= mdl.r[skill]
mdl.const_skill_point = Constraint(required_skills.keys(), rule=const_skill_point)
# 制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
def const_remain_slot_num_armor(mdl, slotlevel):
return sum(mdl.q[eqname]*mdl.p[eqname,slotlevel] for eqname in equip_names) >= 0
mdl.const_remain_slot_num_armor = Constraint(remain_slot_set, rule=const_remain_slot_num_armor)
# 目的関数: 防御力の合計を最大化
def objective(mdl):
return sum(mdl.q[eqname] * mdl.p[eqname, 'deffence'] for eqname in equip_names)
mdl.OBJ = Objective(rule=objective, sense=maximize)
# =============================================================================
# step3. モデルの出力
# =============================================================================
# モデルの詳細を表示
print(mdl.pprint())
# 問題ファイルを出力
import os
output_filename = f"{os.path.splitext(os.path.basename(__file__))[0]}-problem.nl"
mdl.write(output_filename, format="nl", io_options={'symbolic_solver_labels': True})
以上でスキルシミュレーターが完成しました!
前回と同様に以下の手順で実行できます。必須スキルを変更するなどして実験してみてください。
# 問題ファイルを出力
$ cd ~/dmax-from-scratch-sample-code/
$ uv run dmax-mini-3.py
...省略
# 問題ファイルを確認
$ ls -lh | grep dmax-mini-3-prob
-rw-r--r-- 1 dmax-scratch dmax-scratch 634 Aug 15 22:54 dmax-mini-3-problem.col
-rw-r--r-- 1 dmax-scratch dmax-scratch 3.2K Aug 15 22:54 dmax-mini-3-problem.nl
-rw-r--r-- 1 dmax-scratch dmax-scratch 1007 Aug 15 22:54 dmax-mini-3-problem.row
# SCIPソルバーを起動し、問題ファイルを読み込んで最適化
$ rscip
SCIP> read dmax-mini-3-problem.nl
SCIP> optimize
SCIP> display solution
dmax-mini-3.py の実装状況は以下の通りです。
| 実装完了 | 制約条件 | 制約内容 |
|---|---|---|
| ✅ | 制約条件(1) | 各部位で装備できる個数は1以下 (部位は次の7つ 頭・胴・腕・腰・脚・護石・武器) |
| ✅ | 制約条件(2) | ユーザが指定したスキルレベルの条件を満たす |
| ✅ | 制約条件(3) | 装飾品はスロットレベル以上の大きさのスロットにしか装着できない |
| 制約条件(4) | ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ | |
| 制約条件(5) | ダメージ計算式において有効なスキルは装備中のスキルのみ | |
| 制約条件(6) | 会心率の上限は100% |
dmax-mini-4.py
dmax-mini-4.py ではダメージ計算式と制約条件(4), (5), (6)を実装し、最適化シミュを完成させましょう。
dmax-mini-3.py までは目的関数として防御力を利用してきましたが、ダメージ最大化問題の最適化シミュを実装するためには目的関数をダメージ計算式に設定する必要があります。
ダメージ計算式は概ね以下のような形になります。
- こちらは推定されたダメージ計算式です。できるだけゲーム内の計算式に近づけてはありますが、ゲーム内の計算式と一致しない可能性はあります。
- 説明のために登場スキルを絞った計算式になっています。DMAX MHWilds で利用している完全な形のダメージ計算式が知りたい場合は dmax.py を参照してください。
{ (武器倍率) * (第1乗算スキル) + (加算スキル) }
* (第2乗算スキル) * (溜め補正) * (物理肉質) * (ビン補正) * (モーション値) * (会心率補正)
dmax-mini-4.py で扱っているスキルに絞ってダメージ計算式を書くと以下のようになります。
{ (武器倍率) * (ヌシの魂) + (巧撃) + (千刃竜の闘志) + (挑戦者) + (逆襲) }
* (溜め補正) * (物理肉質) * (ビン補正) * (モーション値) * (会心率補正)
ここで、スキル 巧撃 を例にスキルレベルごとの効果を計算式で表現することを考えてみましょう。
巧撃のゲーム内の効果は以下になります。
| Lv | 効果 |
|---|---|
| 1 | スキル発動中、基礎攻撃力+10 |
| 2 | スキル発動中、基礎攻撃力+15 |
| 3 | スキル発動中、基礎攻撃力+20 |
| 4 | スキル発動中、基礎攻撃力+25 |
| 5 | スキル発動中、基礎攻撃力+30 |
この効果を表現するため以下のように定義します。
(巧撃Lv1が発動)の値は 0 か 1 のいずれかを取る(巧撃Lv2が発動)の値は 0 か 1 のいずれかを取る
... Lv3以降も同様
このようにスキルレベルごとに発動の有無を 0 か 1 で表現すると決めておくと、以下のように1つの計算式で 巧撃 スキルの効果を表現できます。
10 * (巧撃Lv1が発動) + 15 * (巧撃Lv2が発動) + 20 * (巧撃Lv3が発動) + 25 * (巧撃Lv4が発動) + 30 * (巧撃Lv5が発動)
例えば、巧撃Lv1が発動したときは (巧撃Lv1が発動)=1 であり、制約条件(4) を実装すれば Lv2 以降は全て0になるので
制約条件(4): ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ
10 * (巧撃Lv1が発動) + 15 * (巧撃Lv2が発動) + 20 * (巧撃Lv3が発動) + 25 * (巧撃Lv4が発動) + 30 * (巧撃Lv5が発動)
= 10 * 1 + 15 * 0 + 20 * 0 + 25 * 0 + 30 * 0
= 10
となり、巧撃Lv1の効果 基礎攻撃力+10 のみが取り出せます。
この定義によって Lv〇 の場合は~ のように条件分岐を書く必要がなくなります。つまり 0, 1 のビット、真偽値をスキルレベルごとに用意することによってスキルレベルによる効果の条件分岐を実装しているということです。
この定義で計算式を書くと以下のようになります。
{ (武器倍率) * (第1乗算スキル) + (加算スキル) }
* (第2乗算スキル) * (溜め補正) * (物理肉質) * (ビン補正) * (モーション値) * (会心率補正)
= { (武器倍率) * (ヌシの魂) + (巧撃) + (千刃竜の闘志) + (挑戦者) + (逆襲) }
* (溜め補正) * (物理肉質) * (ビン補正) * (モーション値) * (会心率補正)
= { ((武器倍率)
* (1.0 + 0.05 * (ヌシの魂Lv3が発動) + 0.05 * (ヌシの魂Lv4が発動) + 0.05 * (ヌシの魂Lv5が発動)))
+ 10 * (巧撃Lv1が発動) + 15 * (巧撃Lv2が発動) + 20 * (巧撃Lv3が発動) + 25 * (巧撃Lv4が発動) + 30 * (巧撃Lv5が発動)
+ 10 * (巧撃Lv1以上が発動) * (千刃竜の闘志Lv4が発動) + 10 * (巧撃Lv1以上が発動) * (千刃竜の闘志Lv5が発動)
+ 4 * (挑戦者Lv1が発動) + 8 * (挑戦者Lv2が発動) + 12 * (挑戦者Lv3が発動) + 16 * (挑戦者Lv4が発動) + 20 * (挑戦者Lv5が発動)
+ 10 * (逆襲Lv1が発動) + 15 * (逆襲Lv2が発動) + 25 * (逆襲Lv3が発動)
} * (溜め補正) * (物理肉質) * (ビン補正) * (モーション値) * (会心率補正)
以下のように、グループスキル ヌシの魂 の効果も実装できていることに注目してください。
グループスキルやシリーズスキルのような一定レベル以上装備することによって発動するスキルは、一定レベル以上に全て同じ係数を実装することで実装できます。
(ヌシの魂の乗算効果)
= (1.0 + 0.05 * (ヌシの魂Lv3が発動) + 0.05 * (ヌシの魂Lv4が発動) + 0.05 * (ヌシの魂Lv5が発動))
さて、ここまでの式変形によってスキルレベルごとのビット表現によりダメージ計算式を立式できました。
この スキルレベルごとのビット表現 は解によって変わる値、つまり変数です。dmax-mini-3.py までの実装では変数としては解を表す変数 mdl.q のみを利用してきました。
# 変数定義: 各装備を何個使うかを表す変数
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
変数 mdl.q は各装備を何個使うかを表す変数であり、各装備にはスキル属性が付いているため、変数 mdl.q のみでも スキルレベルごとのビット表現 を導出することはできると思いますが、難しそうです。
そこで、補助変数として ダメージ寄与スキルのレベルごとのビット変数 を導入し、ダメージ計算式に必要な変数を直接的に表現できるようにします。
ダメージ寄与スキルのレベルごとのビット変数 を補助変数 mdl.x とすると以下のように実装できます。mdl.x は2次元配列の変数です。mdl.x['弱点特効', 3] のように [スキル名, スキルレベル] という形式のインデックスでアクセスし、 mdl.x['弱点特効', 3] = 1 ならば弱点特効Lv3が発動すると解釈します。
# ダメージ計算式に登場するスキル名の集合
damage_skill_set = { "ヌシの魂", "巧撃", "千刃竜の闘志", "挑戦者", "逆襲", "弱点特効", "力の解放", "渾身", "海竜の渦雷"}
# スキルレベルのインデックスをモデルに追加 (すべて最大レベル7に統一)
mdl.I = RangeSet(0, 7)
# 変数定義: ダメージ寄与スキルのレベルを表す補助変数
# 例: mdl.x['弱点特効', 3] = 1 ならば 弱点特効Lv3 が発動
# mdl.x['弱点特効', 1] = 0 ならば 弱点特効Lv1 が発動しない
mdl.x = Var(damage_skill_set, mdl.I, within=Boolean)
スキル名側のインデックスはダメージ計算式に寄与するスキルの一覧です。コード中では damage_skill_set として定義しています。
スキルレベル側のインデックスは Lv0 ~ Lv7 までのスキルレベルです。
スキルレベルのインデックスは普通のリストとして [0, 1, 2, 3, 4, 5, 6, 7] のように定義してもよいですが、Pyomo には RangeSet という連続整数の集合を定義するための専用クラスがあるので、こちらを利用しましょう。
RangeSet クラスを利用すると、スキルレベルのインデックスは RangeSet(0, 7) と定義できます。
- スキルが発動しないことを表現するために
Lv0が必要です - 全てのスキルを同じ形式で処理するために、全スキルの最大レベルを
Lv7と定義しています
巧撃などは最大レベルがLv5でありLv7は存在しないのですが、あっても困らない上に楽に実装できるようになるのでLv7まで定義しておきましょう。その分変数は増えますが、きっと最適化ソルバーを通せば誤差になると思います。
補助変数 mdl.x を導入することによってダメージ計算式は以下のように表現できます。
(会心率補正については式が複雑になるため一旦除外しています。後ほど実装します。)
# ダメージ計算に利用する設定値
cp = {
"武器倍率" : 210,
"武器会心率" : 25,
"溜め補正物理": 1.1, # 溜めLv3 剛連射の数値を利用
"モーション値": 14, # 溜めLv3 剛連射の数値を利用
"ビン補正" : 0.4, # 接撃ビンの補正値を利用
"物理肉質" : 45,
}
# 目的関数: ダメージ計算式を最大化
def objective(mdl):
return (((cp['武器倍率'] \
* (1.0 + 0.05*mdl.x['ヌシの魂',3] + 0.05*mdl.x['ヌシの魂',4] + 0.05*mdl.x['ヌシの魂',5])) \
+ (10*mdl.x['巧撃',1] + 15*mdl.x['巧撃',2] + 20*mdl.x['巧撃',3] + 25*mdl.x['巧撃',4] + 30*mdl.x['巧撃',5]) \
+ (1 - mdl.x['巧撃', 0]) * (10*mdl.x['千刃竜の闘志',4] + 10*mdl.x['千刃竜の闘志',5]) \
+ (4*mdl.x['挑戦者',1] + 8*mdl.x['挑戦者',2] + 12*mdl.x['挑戦者',3] + 16*mdl.x['挑戦者',4] + 20*mdl.x['挑戦者',5]) \
+ (10*mdl.x['逆襲',1] + 15*mdl.x['逆襲',2] + 25*mdl.x['逆襲',3]) \
) \
* (cp['溜め補正物理']/100.0) \
* (cp['物理肉質']/100.0) \
* (1.0 + cp['ビン補正']) \
* (cp['モーション値']) \
)
制約条件がない状態で最適化した場合、目的関数を最大化するため全ての mdl.x[skillName, skillLevel] に 1 が立つでしょう。巧撃 スキルの場合はLv1からLv5までを全部発動させて (10 + 15 + 20 + 25 + 30) = 100 の攻撃力加算値を得るのが最適です。
しかし実際のゲーム内では同一スキルのうち発動できるスキルレベルは1以下という暗黙の条件があるため、これを実装する必要があります。つまり制約条件(4)が必要です。
制約条件(4): ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ
補助変数 mdl.x を利用して制約条件(4)を実装すると以下のようになります。
以下では damage_skill_set つまりダメージ計算式に寄与するスキルの全てについて、制約条件式(4) const_skill_level_total を定義しています。
# 制約条件(4): ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ
def const_skill_level_total(mdl, skill):
return sum(mdl.x[skill, i] for i in mdl.I) == 1 # <= 1 でもいいかもしれない
mdl.const_skill_level_total = Constraint(damage_skill_set, rule=const_skill_level_total)
以上の実装によって、同名スキルのうち1つのレベルだけがダメージ計算式内で発動するようにできました。
さて、基本的にスキルレベルは高いほうがより高いダメージが得られます。したがって、このままでは全スキルで最大レベルを発動させるのが最適となってしまいます。しかし、実際のゲーム内では 発動するスキルは装備している装備に付いているスキルのみ、という暗黙の条件があるため、これを実装する必要があります。つまり制約条件(5)が必要です。
制約条件(5): ダメージ計算式において有効なスキルは装備中のスキルのみ
スキル 巧撃 を例に取って考えます。
スキル 巧撃 はできるだけ高いレベルを発動したいですが、発動できるスキルレベルは 装備している装備に付いている 巧撃 スキルのレベルの合計 によって上から抑えられます。つまり (装備中の巧撃スキルのレベルの合計) がダメージ計算式内で発動可能な 巧撃 スキルの上限になります。
よって、以下のような制約式が欲しいです。
(装備中の巧撃スキルのレベルの合計) >= (ダメージ計算式内の巧撃スキルのレベル)
こちらを変数 mdl.q と mdl.x を利用して表現すると以下のようになります。
def const_skill_bridge_adrenaline_rush(mdl):
return sum(mdl.q[eqname]*mdl.p[eqname, '巧撃'] for eqname in equip_names) \
>= sum(mdl.I[i+1]*mdl.x['巧撃', i] for i in mdl.I)
mdl.const_skill_bridge_adrenaline_rush = Constraint(rule=const_skill_bridge_adrenaline_rush)
damage_skill_set の全てのスキルについてまとめて定義すると以下のようになります。
# ダメージ計算式に登場するスキル名の集合
damage_skill_set = {"ヌシの魂", "巧撃", "千刃竜の闘志", "挑戦者", "逆襲", "弱点特効", "力の解放", "渾身", "海竜の渦雷",}
# 制約条件(5): ダメージ計算式において有効なスキルは装備中のスキルのみ
# 例: (装備中の挑戦者スキルのレベルの合計) >= (ダメージ計算内の挑戦者スキルのレベル)
def const_skill_bridge(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname, skill] for eqname in equip_names) \
>= sum(mdl.I[i+1]*mdl.x[skill, i] for i in mdl.I)
mdl.const_skill_bridge = Constraint(damage_skill_set, rule=const_skill_bridge)
最後に会心率補正を考えます。
会心率は (会心率) = (武器の会心率) + (スキルの会心率) で計算できます。
ただし会心率の上限は100%なので min(100, 会心率) が必要です。
これらを2つの制約式で表すと以下のようになります。
会心率の制約式1: (会心率) <= 100
会心率の制約式2: (会心率) <= (武器の会心率) + (スキルの会心率)
会心率の制約式1 は制約条件(6)ですね。
会心率の制約式2 はダメージ計算式の一部です。
制約条件(6): 会心率の上限は100%
(会心率の制約式2 は制約条件(7)としても良かったのですが、制約条件というよりダメージ計算式の一部だろうと思い、制約条件のリストから外しました。)
会心率についても同様に補助変数を導入して立式を簡単にしましょう。
会心率を表す補助変数 mdl.afr を以下のように導入し、2つの制約条件を実装します。
# 変数定義: 会心率を表す補助変数
# min(100, 会心率) を実現するために必要
mdl.afr = Var(within=NonNegativeIntegers)
# 制約条件(6): 会心率の上限は100%
def const_max_affinity_1(mdl):
return mdl.afr <= 100
mdl.const_max_affinity_1 = Constraint(rule=const_max_affinity_1)
# 制約条件: ダメージ計算式の会心率部分を制約条件として実装
# mdl.afr <= (武器会心+スキル会心の合計)
def const_max_affinity_2(mdl):
return mdl.afr <= \
(cp['武器会心率'] \
+ (3*mdl.x['挑戦者',1] + 5*mdl.x['挑戦者',2] + 7*mdl.x['挑戦者',3] + 10*mdl.x['挑戦者',4] + 15*mdl.x['挑戦者',5]) \
+ (5*mdl.x['弱点特効',1] + 10*mdl.x['弱点特効',2] + 15*mdl.x['弱点特効',3] + 20*mdl.x['弱点特効',4] + 30*mdl.x['弱点特効',5]) \
+ (10*mdl.x['力の解放',1] + 20*mdl.x['力の解放',2] + 30*mdl.x['力の解放',3] + 40*mdl.x['力の解放',4] + 50*mdl.x['力の解放',5]) \
+ (10*mdl.x['渾身',1] + 20*mdl.x['渾身',2] + 30*mdl.x['渾身',3]) \
+ (15*mdl.x['海竜の渦雷',2] + 15*mdl.x['海竜の渦雷',3] + 15*mdl.x['海竜の渦雷',4] + 15*mdl.x['海竜の渦雷',5]) \
)
mdl.const_max_affinity_2 = Constraint(rule=const_max_affinity_2)
以上で、会心率を表す補助変数 mdl.afr の準備ができたので、目的関数のダメージ計算式に追加します。
会心補正は、会心が発動した時に 1.25 倍になり、発動しなかった場合は 1.0 倍です。
発動率は mdl.afr なので目的関数は以下のようになります。
# 目的関数: ダメージ計算式を最大化
def objective(mdl):
return (((cp['武器倍率'] \
* (1.0 + 0.05*mdl.x['ヌシの魂',3] + 0.05*mdl.x['ヌシの魂',4] + 0.05*mdl.x['ヌシの魂',5])) \
+ (10*mdl.x['巧撃',1] + 15*mdl.x['巧撃',2] + 20*mdl.x['巧撃',3] + 25*mdl.x['巧撃',4] + 30*mdl.x['巧撃',5]) \
+ (1 - mdl.x['巧撃', 0]) * (10*mdl.x['千刃竜の闘志',4] + 10*mdl.x['千刃竜の闘志',5]) \
+ (4*mdl.x['挑戦者',1] + 8*mdl.x['挑戦者',2] + 12*mdl.x['挑戦者',3] + 16*mdl.x['挑戦者',4] + 20*mdl.x['挑戦者',5]) \
+ (10*mdl.x['逆襲',1] + 15*mdl.x['逆襲',2] + 25*mdl.x['逆襲',3]) \
) \
* (cp['溜め補正物理']/100.0) \
* (cp['物理肉質']/100.0) \
* (1.0 + cp['ビン補正']) \
* (cp['モーション値']) \
+ * (1.0 + (mdl.afr/100.0) * (1.25 - 1.0)) \
)
dmax-mini-4.py のソースコード全体は以下のようになります。
サンプルコードのリポジトリでは以下から dmax-mini-4.py を確認できます。
# dmax-mini-4.py: 制約条件(1)-(6) と ダメージ計算式 を実装
from pyomo.environ import *
# =============================================================================
# step1. 入力データ読み込み: 装備データの2次元配列作成、配列のインデックス作成
# =============================================================================
# 全ての装備データ (防具、護石、装飾品)
equip_all = [
{"type": "head", "name": "レダゼルトヘルムγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "弱点特効": 1, "渾身": 1, "スタミナ急速回復": 1}},
{"type": "torso", "name": "レダゼルトメイルγ", "deffence": 68, "slots": [1, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 3}},
{"type": "arms", "name": "レダゼルトアームγ", "deffence": 68, "slots": [3, 3, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "回避距離UP": 2}},
{"type": "waist", "name": "レダゼルトコイルγ", "deffence": 68, "slots": [0, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "力の解放": 2, "渾身": 2}},
{"type": "legs", "name": "レダゼルトグリーヴγ", "deffence": 68, "slots": [3, 0, 0], "skills": {"煌雷竜の力": 1, "ヌシの魂": 1, "スタミナ急速回復": 2, "気絶耐性": 3}},
{"type": "head", "name": "ラギアヘルムα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "渾身": 2, "力の解放": 1, "革細工の柔性": 1}},
{"type": "torso", "name": "ラギアメイルα", "deffence": 64, "slots": [2, 1, 0], "skills": {"海竜の渦雷": 1, "雷耐性": 2, "弱点特効": 1, "スタミナ急速回復": 1, "革細工の柔性": 1}},
{"type": "arms", "name": "ラギアアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"海竜の渦雷": 1, "スタミナ急速回復": 2, "弱点特効": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "waist", "name": "ラギアコイルα", "deffence": 64, "slots": [2, 1, 1], "skills": {"海竜の渦雷": 1, "弱点特効": 1, "渾身": 1, "水場・油泥適応": 1, "革細工の柔性": 1}},
{"type": "legs", "name": "ラギアグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"海竜の渦雷": 1, "弱点特効": 2, "力の解放": 1, "雷耐性": 1, "革細工の柔性": 1}},
{"type": "head", "name": "レギオスヘルムα", "deffence": 64, "slots": [3, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 1, "逆襲": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "torso", "name": "レギオスメイルα", "deffence": 64, "slots": [1, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "逆襲": 1, "鱗張りの技法": 1}},
{"type": "arms", "name": "レギオスアームα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "回避距離UP": 1, "鱗張りの技法": 1}},
{"type": "waist", "name": "レギオスコイルα", "deffence": 64, "slots": [2, 0, 0], "skills": {"千刃竜の闘志": 1, "回避性能": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "legs", "name": "レギオスグリーヴα", "deffence": 64, "slots": [0, 0, 0], "skills": {"千刃竜の闘志": 1, "巧撃": 2, "挑戦者": 1, "裂傷耐性": 1, "鱗張りの技法": 1}},
{"type": "charm", "name": "挑戦の護石Ⅱ", "slots": [0,0,0], "skills": {"挑戦者": 2}},
{"type": "charm", "name": "反攻の護石Ⅲ", "slots": [0,0,0], "skills": {"巧撃": 3}},
{"type": "decoArmor", "name": "反攻珠【3】", "size": 3, "skills": {"巧撃": 1}},
{"type": "decoArmor", "name": "逆襲珠【2】", "size": 2, "skills": {"逆襲": 1}},
{"type": "decoArmor", "name": "痛撃珠【3】", "size": 3, "skills": {"弱点特効": 1}},
{"type": "decoArmor", "name": "渾身珠【2】", "size": 2, "skills": {"渾身": 1}},
{"type": "decoArmor", "name": "体術珠【1】", "size": 1, "skills": {"体術": 1}},
{"type": "decoArmor", "name": "早気珠【2】", "size": 2, "skills": {"スタミナ急速回復": 1}},
{"type": "decoArmor", "name": "挑戦珠【3】", "size": 3, "skills": {"挑戦者": 1}},
{"type": "decoArmor", "name": "全開珠【3】", "size": 3, "skills": {"力の解放": 1}},
]
# 装備の名前集合 (2次元配列 p(i, j) の i の集合)
equip_names = set()
# 1つしか装備できない装備タイプの集合
single_equip_type_set = {'head', 'torso', 'arms', 'waist', 'legs', 'charm'}
# 装飾品スロットの属性
remain_slot_set = {'Lv123RemainSlotNum', 'Lv23RemainSlotNum', 'Lv3RemainSlotNum'}
# 装備の全属性の集合 (2次元配列 p(i, j) の j の集合)
attribute_set = set()
attribute_set = attribute_set | single_equip_type_set | {'deffence'} | {'decoArmor'} | remain_slot_set
# 存在するスキルの集合 (後ほど 制約条件(4) の実装で利用)
skill_set = set()
for equip in equip_all:
# 装備名の集合に追加
equip_names.add(equip['name'])
# 属性の集合に追加
for skill in equip['skills']:
attribute_set.add(skill)
skill_set.add(skill)
# 装備データの2次元配列を作成 ( p(i, j) の定義に利用 )
eqinfo_matrix = {}
for equip in equip_all:
# 装備タイプの属性データを追加
# 例: eqinfo_matrix['レダゼルトヘルムγ', 'head'] = 1
eqinfo_matrix[equip['name'], equip['type']] = 1
# 装備についているスキルの属性データを追加
# 例: eqinfo_matrix['反攻の護石Ⅲ', '巧撃'] = 3
for skill in equip['skills']:
eqinfo_matrix[equip['name'], skill] = equip['skills'][skill]
# 装備の防御力を追加
eqinfo_matrix[equip['name'], 'deffence'] = equip['deffence'] if 'deffence' in equip else 0
# 装飾品の残りスロット属性を追加
if equip['type'] == 'decoArmor':
eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = -1 if equip['size'] >= 1 else 0
eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = -1 if equip['size'] >= 2 else 0
eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = -1 if equip['size'] >= 3 else 0
# 装備の残りスロット属性を追加
if equip['type'] in single_equip_type_set:
eqinfo_matrix[equip['name'], 'Lv123RemainSlotNum'] = len(list(filter(lambda n: n >= 1, equip['slots'])))
eqinfo_matrix[equip['name'], 'Lv23RemainSlotNum'] = len(list(filter(lambda n: n >= 2, equip['slots'])))
eqinfo_matrix[equip['name'], 'Lv3RemainSlotNum'] = len(list(filter(lambda n: n >= 3, equip['slots'])))
# ユーザが指定する必須スキルレベルのデータ
required_skills = {
"巧撃": 0,
"挑戦者": 0,
"逆襲": 0,
"弱点特効": 0,
"渾身": 0,
"力の解放": 0,
"煌雷竜の力": 0,
"ヌシの魂": 0,
"海竜の渦雷": 0,
"千刃竜の闘志": 0,
"スタミナ急速回復": 3,
"体術": 5,
"回避距離UP": 0,
"気絶耐性": 0,
"革細工の柔性": 0,
"雷耐性": 0,
"水場・油泥適応": 0,
"裂傷耐性": 0,
"鱗張りの技法": 0,
"回避性能": 0,
}
# ダメージ計算式に登場するスキル名の集合
damage_skill_set = {
"ヌシの魂",
"巧撃",
"千刃竜の闘志",
"挑戦者",
"逆襲",
"弱点特効",
"力の解放",
"渾身",
"海竜の渦雷",
}
# ダメージスキルのうち、装備に存在するスキルのみの集合 (入力エラー対策のため)
available_damage_skills = damage_skill_set & skill_set
# ダメージ計算に利用する設定値
cp = {
"武器倍率" : 210,
"武器会心率" : 25,
"溜め補正物理": 1.1, # 溜めLv3 剛連射の数値を利用
"モーション値": 14, # 溜めLv3 剛連射の数値を利用
"ビン補正" : 0.4, # 接撃ビンの補正値を利用
"物理肉質" : 45,
}
# =============================================================================
# step2. モデルの定義: パラメータ、変数、制約条件、目的関数の追加
# =============================================================================
# モデル定義: 空のモデルを作成
mdl = ConcreteModel(name="dmax model", doc="model for solving damage optimization problem")
# パラメータ定義: 装備データの2次元配列パラメータ
mdl.p = Param(equip_names, attribute_set, default=0, initialize=eqinfo_matrix, within=Integers)
# 変数定義: 各装備を何個使うかを表す変数
mdl.q = Var(equip_names, within=NonNegativeIntegers, initialize=0)
# 制約条件(1): 各部位で使用できる装備の数は 1 以下
def const_total_equipment_type(mdl, eqtype):
return sum(mdl.q[eqname]*mdl.p[eqname,eqtype] for eqname in equip_names) <= 1
mdl.const_total_equipment_type = Constraint(single_equip_type_set, rule=const_total_equipment_type)
# パラメータ定義: ユーザが指定した必須スキルレベル
mdl.r = Param(required_skills.keys(), default=0, initialize=required_skills, within=Integers)
# 制約条件(2): ユーザが指定したスキルレベルの条件を満たす
def const_skill_point(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname,skill] for eqname in equip_names) >= mdl.r[skill]
mdl.const_skill_point = Constraint(required_skills.keys(), rule=const_skill_point)
# 制約条件(3): 装飾品はスロットレベル以上の大きさのスロットにしか装着できない
def const_remain_slot_num_armor(mdl, slotlevel):
return sum(mdl.q[eqname]*mdl.p[eqname,slotlevel] for eqname in equip_names) >= 0
mdl.const_remain_slot_num_armor = Constraint(remain_slot_set, rule=const_remain_slot_num_armor)
# スキルレベルのインデックスをモデルに追加 (すべて最大レベル7に統一)
mdl.I = RangeSet(0, 7)
# 変数定義: ダメージ寄与スキルのレベルを表す補助変数
# 例: mdl.x['弱点特効', 3] = 1 ならば 弱点特効Lv3 が発動
# mdl.x['弱点特効', 1] = 0 ならば 弱点特効Lv1 が発動しない
mdl.x = Var(damage_skill_set, mdl.I, within=Boolean)
# 変数定義: 会心率を表す補助変数
# min(100, 会心率) を実現するために必要
mdl.afr = Var(within=NonNegativeIntegers)
# 制約条件(4): ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ
def const_skill_level_total(mdl, skill):
return sum(mdl.x[skill, i] for i in mdl.I) == 1 # <= 1 でもいいかもしれない
mdl.const_skill_level_total = Constraint(damage_skill_set, rule=const_skill_level_total)
# 制約条件(5): ダメージ計算式において有効なスキルは装備中のスキルのみ
# スキルシミュ側とダメージ計算に利用するスキルポイント数を結びつける制約式
# 例: (装備中の挑戦者スキルのレベルの合計) >= (ダメージ計算内の挑戦者スキルのレベル)
def const_skill_bridge(mdl, skill):
return sum(mdl.q[eqname]*mdl.p[eqname, skill] for eqname in equip_names) \
>= sum(mdl.I[i+1]*mdl.x[skill, i] for i in mdl.I)
mdl.const_skill_bridge = Constraint(available_damage_skills, rule=const_skill_bridge)
# 制約条件(6): 会心率の上限は100%
def const_max_affinity_1(mdl):
return mdl.afr <= 100
mdl.const_max_affinity_1 = Constraint(rule=const_max_affinity_1)
# 制約条件: ダメージ計算式の会心率部分を制約条件として実装
# mdl.afr <= (武器会心+スキル会心の合計)
def const_max_affinity_2(mdl):
return mdl.afr <= \
(cp['武器会心率'] \
+ (3*mdl.x['挑戦者',1] + 5*mdl.x['挑戦者',2] + 7*mdl.x['挑戦者',3] + 10*mdl.x['挑戦者',4] + 15*mdl.x['挑戦者',5]) \
+ (5*mdl.x['弱点特効',1] + 10*mdl.x['弱点特効',2] + 15*mdl.x['弱点特効',3] + 20*mdl.x['弱点特効',4] + 30*mdl.x['弱点特効',5]) \
+ (10*mdl.x['力の解放',1] + 20*mdl.x['力の解放',2] + 30*mdl.x['力の解放',3] + 40*mdl.x['力の解放',4] + 50*mdl.x['力の解放',5]) \
+ (10*mdl.x['渾身',1] + 20*mdl.x['渾身',2] + 30*mdl.x['渾身',3]) \
+ (15*mdl.x['海竜の渦雷',2] + 15*mdl.x['海竜の渦雷',3] + 15*mdl.x['海竜の渦雷',4] + 15*mdl.x['海竜の渦雷',5]) \
)
mdl.const_max_affinity_2 = Constraint(rule=const_max_affinity_2)
# 目的関数: ダメージ計算式を最大化
def objective(mdl):
return (((cp['武器倍率'] \
* (1.0 + 0.05*mdl.x['ヌシの魂',3] + 0.05*mdl.x['ヌシの魂',4] + 0.05*mdl.x['ヌシの魂',5])) \
+ (10*mdl.x['巧撃',1] + 15*mdl.x['巧撃',2] + 20*mdl.x['巧撃',3] + 25*mdl.x['巧撃',4] + 30*mdl.x['巧撃',5]) \
+ (1 - mdl.x['巧撃', 0]) * (10*mdl.x['千刃竜の闘志',4] + 10*mdl.x['千刃竜の闘志',5]) \
+ (4*mdl.x['挑戦者',1] + 8*mdl.x['挑戦者',2] + 12*mdl.x['挑戦者',3] + 16*mdl.x['挑戦者',4] + 20*mdl.x['挑戦者',5]) \
+ (10*mdl.x['逆襲',1] + 15*mdl.x['逆襲',2] + 25*mdl.x['逆襲',3]) \
) \
* (cp['溜め補正物理']/100.0) \
* (cp['物理肉質']/100.0) \
* (1.0 + cp['ビン補正']) \
* (cp['モーション値']) \
* (1.0 + (mdl.afr/100.0) * (1.25 - 1.0)) \
)
# 目的関数をモデルに設定
mdl.OBJ = Objective(rule=objective, sense=maximize)
# =============================================================================
# step3. モデルの出力
# =============================================================================
# モデルの詳細を表示
print(mdl.pprint())
# 問題ファイルを出力
import os
output_filename = f"{os.path.splitext(os.path.basename(__file__))[0]}-problem.nl"
mdl.write(output_filename, format="nl", io_options={'symbolic_solver_labels': True})
以上で dmax-mini-4.py の実装が完了し、最適化シミュに必要な制約条件を一通り実装できました。
| 実装完了 | 制約条件 | 制約内容 |
|---|---|---|
| ✅ | 制約条件(1) | 各部位で装備できる個数は1以下 (部位は次の7つ 頭・胴・腕・腰・脚・護石・武器) |
| ✅ | 制約条件(2) | ユーザが指定したスキルレベルの条件を満たす |
| ✅ | 制約条件(3) | 装飾品はスロットレベル以上の大きさのスロットにしか装着できない |
| ✅ | 制約条件(4) | ダメージ計算式において有効な同名スキルのスキルレベルは1つのみ |
| ✅ | 制約条件(5) | ダメージ計算式において有効なスキルは装備中のスキルのみ |
| ✅ | 制約条件(6) | 会心率の上限は100% |
それでは dmax-mini-4.py を実行し、出力された問題ファイルをSCIPソルバーで最適化してみましょう。
# 問題ファイルの作成
$ uv run dmax-mini-4.py
# 問題ファイルの確認
$ ls -lh | grep dmax-mini-4-prob
# SCIPソルバーを起動し、問題ファイルを読み込んで最適化
$ rscip
SCIP> read dmax-mini-4-problem.nl
SCIP> optimize
SCIP> display solution
結果は以下のようになりました。指定された条件において実現可能な最大ダメージは 32.49 であり、そのダメージを実現できる装備構成が表示されていることがわかります。
SCIP> display solution
objective value: 32.4924831
x[ヌシの魂,0] 1 (obj:0)
x[力の解放,1] 1 (obj:0)
x[千刃竜の闘志,0] 1 (obj:0)
x[弱点特効,3] 1 (obj:0)
x[海竜の渦雷,2] 1 (obj:0)
x[渾身,3] 1 (obj:0)
x[巧撃,5] 1 (obj:0)
x[挑戦者,1] 1 (obj:0)
x[逆襲,3] 1 (obj:0)
afr 98 (obj:0)
q[ラギアアームα] 1 (obj:0)
q[ラギアコイルα] 1 (obj:0)
q[ラギアヘルムα] 1 (obj:0)
q[ラギアメイルα] 1 (obj:0)
q[レギオスグリーヴα] 1 (obj:0)
q[体術珠【1】] 5 (obj:0)
q[反攻の護石Ⅲ] 1 (obj:0)
q[逆襲珠【2】] 3 (obj:0)
nlobjvar 32.4924831 (obj:1)
| 部位 | 装備名 | スロット | 装飾品 |
|---|---|---|---|
| 頭 | ラギアヘルムα | 2-1-0 | 逆襲珠【2】, 体術珠【1】 |
| 胴 | ラギアメイルα | 2-1-0 | 逆襲珠【2】, 体術珠【1】 |
| 腕 | ラギアアームα | 2-0-0 | 逆襲珠【2】 |
| 腰 | ラギアコイルα | 2-1-1 | 体術珠【1】, 体術珠【1】, 体術珠【1】 |
| 脚 | レギオスグリーヴα | 0-0-0 | |
| 護石 | 反攻の護石Ⅲ | 0-0-0 |
required_skills においてユーザに指定された体術Lv5やスタミナ急速回復Lv3などの必須スキルを揃えた上で、強そうなスキル構成の装備が表示されています。
残念ながら、これが最適解かどうかを調べるのは難しいです。全探索の際にも話した通り、組み合わせ数が多すぎて全部を試すことはできないからです。ただし、スキルシミュレーターのときと違い、dmax-mini-4.py では required_skills においてダメージが上がりそうなスキルを一切指定していません。にもかかわらず、
-
巧撃、逆襲、弱点特効などの発動条件が難しい代わりに効果の高いダメージスキルが集中的に採用されている点 - 装飾品もスロット枠をめいっぱい使いダメージを上げるスキルが採用した構成が示されている点
を考慮すると実現可能な装備の中でダメージの最大化を指向して最適化された結果であることは見て取れます。
required_skills は武器を運用するためにやむを得ず指定するスキルです。したがって required_skills の制限を緩めれば最大ダメージは向上することが期待できます。
ぜひ、実験として required_skills の指定レベルを全て0にして最大ダメージが向上するかどうか試してみてください。
💡 最適解を検証するには
最適化シミュの結果がどの程度有用かを検証するためには、タイムアタック動画 (TA動画) を指標にすると良いです。
装備の詳細や使用したバフなどが収められているTA動画を見つけて、条件を揃えて最適化シミュに入力します。得られた最適化結果のダメージが、動画内の実際のダメージとどの程度ズレているかをチェックすると良いでしょう。
TA動画を投稿しているようなプレイヤーの方は、ダメージの出し方に対する理解が深く、またスキルシミュを利用していることも多いです。したがって、最適化シミュで最適解を得たとしても、動画内のダメージを大幅に上回るような結果はまず得られません。むしろ大幅に上回った場合は、実装にミスがないかを疑ったほうが良いでしょう。
dmax.py
dmax-mini-4.py では最適化シミュに必要な全ての要素を実装していますが、装備やスキルデータを絞っているためその分の実装が不足しています。
この不足分を全て実装したものが dmax.py になります。
サンプルコードのリポジトリでは以下から dmax.py を確認できます。
dmax-mini-4.py と dmax.py の主な差分は以下です。いずれも、dmax-mini-4.py までの解説の応用で実装可能だと思います。
| 差分 | 対応方法 |
|---|---|
| 装備とスキルデータを全て追加 | 件数が多いため data-dmax-input.json というデータファイルから読み込むように変更 |
| 武器装飾品の制約条件を追加 | 防具装飾品と同等の制約条件 const_remain_slot_num_weapon を追加 |
| 追加されたスキルをダメージ計算式に追加 | 攻撃力系スキルに加えて属性スキルもダメージ計算式に追加 |
dmax.py では2025年7月23日時点のモンハンワイルズの装備データとゲーム内の仕様を全て実装に反映しており、Web で公開している DMAX MHWilds の ver.4.1.0 に対応しています。
2025年8月13日にモンハンワイルズのアップデートがあり、鑑定護石という仕様が追加されました。dmax.py は鑑定護石には対応していません。鑑定護石への対応は良い練習になると思うので、ぜひどうすれば実装できるか考えて実装してみてください。
ちなみに DMAX MHWilds は ver.5.0.0 で鑑定護石に対応しています。
DMAX では最適化ソルバーに最適化処理を丸投げできるおかげで、この鑑定護石の対応には検証を含めても1時間かかっておらず、アプデの前日に修正が完了していました。最適化ソルバー最高です!
ただ、アプデの内容によっては最適化ソルバーの制限が逆に負担になることもあるかもしれません。もしかすると実装不可能な仕様等もでてくるかもしれません。このあたりは良し悪しですね。
最適化シミュをユーザに届けるまでのハードル
dmax.py までで最適化シミュは完成していますが、この状態で提供するとユーザにとっては不便です。
このセクションではユーザ提供までの残りのハードルを簡単に整理します。
最適化処理の実行環境
まず、dmax.py と SCIPソルバー を動かすためには環境構築が必要です。ユーザに提供するためにはこの実行環境のセットアップを一発で済むようにする必要があります。実行環境の選択肢としてはデスクトップアプリ、スマートフォンアプリ、Webアプリなどがあります。
DMAX MHWilds の実行環境としてWebアプリを選択したのは、この形式が最も多くの環境で動くからです。ブラウザさえあればどんなOSでもどんな端末でも基本的に動くというのがWebアプリの強みです。
Webアプリを選択した場合「SCIPソルバーをどこで動かすか?」という問題があります。Webアプリをホストしているサーバ側で動かすのなら簡単ですが、それをやってしまうと複数のユーザが同時に最適化処理を実行したときにWebサーバの計算資源が枯渇してしまいます。
これを避けるためにネイティブアプリを選択して、各端末上でSCIPソルバーを動かすというのも手です。ただし、その場合は iOS, Android, Windows, macOS などの環境ごとにアプリを提供する必要が発生します。工数的にどこかを妥協することになるかもしれません。
DMAX MHWilds での解決方法は WebAssembly です。ソースコードから wasm バイナリとしてSCIPソルバーをビルドし、各端末のブラウザ上でSCIPソルバーを実行しています。この辺りの話はまた機会があれば書きたいと思っています。
UIを実装する
dmax.py にはユーザが入力するためのボタンなどのUIがありません。
UIでの入力は実質的にデータファイルを修正するのと変わらないのですが、「データファイルを手で修正してね」というアプリをユーザに提供しても不便すぎて利用されないでしょう。
UIの実装方法はアプリの実行環境に依存します。
DMAX MHWilds では実行環境としてWebアプリを選択しており、UIの実装には React フレームワークを利用しています。React を利用するとボタンやスライダーなどのよく利用するパーツを、他のライブラリから流用することができます。例えばMUIのような出来合いのパーツを提供しているライブラリがあり、これをインストールすることでそのまま利用できるので工数を削減できます。
ダメージ計算式を割り出す
別武器に対応させるためにはその武器のダメージ計算式が必要になります。
ダメージ計算式は公式に発表されているわけではないので、推定する必要があります。これが一番泥臭くて大変な部分になります。
本記事ではダメージ計算式の推定方法は扱っていませんが、基本的には以下のようなゲーム上の表示と推定の計算式による結果をすり合わせていく作業になります。
- 武器のパラメータ表示
- スキルの説明文
- ステータス表示
- モンスターを攻撃したときの実際のダメージ
参考文献
最後に最適化シミュレーターを実装する上で参考になる文献をまとめておきます。
線型計画法を用いたスキルシミュレーター作成のための文書
DMAX MHWilds の実装はほぼ全てこのドキュメントをベースにしています。このドキュメント内では「モンハンのスキルシミュは線形計画問題に帰着させて解くことができる」ということが述べられており、その具体的な方法まで書かれています。DMAX はこの手法にダメージ計算式と非線形整数計画ソルバーを導入し、Webアプリとして実装したものになります。
文章は簡潔でわかりやすいです。
ベクトルや行列が登場するので数学アレルギーがあると少しとっつきにくいかもしれませんが、実質的には掛け算と足し算しかしていません。記法さえ覚えれば問題なく読めると思うのでぜひ読んでみてください。
整数計画法でモンハンのスキルシミュを実装する
上記の 線型計画法を用いたスキルシミュレーター作成のための文書 をベースにWebアプリとして実装されたスキルシミュの解説記事です。
スキルシミュの解説を本記事よりもっと簡潔に読みたい人にオススメです。
Webアプリのソースコードも公開されているので、アプリの実装まで考えている方はぜひ参考にしてみてください。
Pyomo×SCIPは組合せ最適化にて最強… 覚えておけ
さまざまなモデリングツールと最適化ソルバーを比較し、Pyomo モデリングツールと SCIP 最適化ソルバーの組み合わせが最強であることが紹介されています。
また、モンハンではなく組合せ最適化一般の文脈で、複雑な問題に対する実装のアプローチが解説されているので、ぜひそちらも参考にしてみてください。
【MHWI】最強装備の自動シミュレータを作ってみた!!
私が知る限り最初の、モンハンにおける自動ダメージ最大化シミュレーターの実装です。
ソースコードは以下で公開されていますが、実行環境として Matlab という有料ソフトウェアが必要です。(かなり高額なソフトなので私も試せていないです)
あとがき
モンハンの最適化シミュやスキルシミュについて、自分が知る限り詳しく書き残しておきたいと思いこの記事を書きました。この記事を読んで自作シミュに興味を持つ人が増えてくれるとうれしいですし、自作してくれたらもっとうれしいです!
自作する場合は環境構築の部分だけでも早めに済ませてしまうことをオススメします。環境構築の手順書というものには消費期限があり、時間が経つと同じ手順で環境を再現するのがどんどん難しくなっていってしまうからです。
本記事とサンプルコードのプログラムは断りなく利用してかまいませんが、使用報告があるとうれしいので差し支えなければご一報ください。
わからない点があればぜひ質問してください。DMでもOKです。
フォローを返せていない場合はお手数ですがその旨ご連絡ください。
また、もし記事中にミス等があればご連絡いただけますと幸いです。
ではまた。