[C#]45°回転した楕円の接線の交点を求めたい
解決したいこと
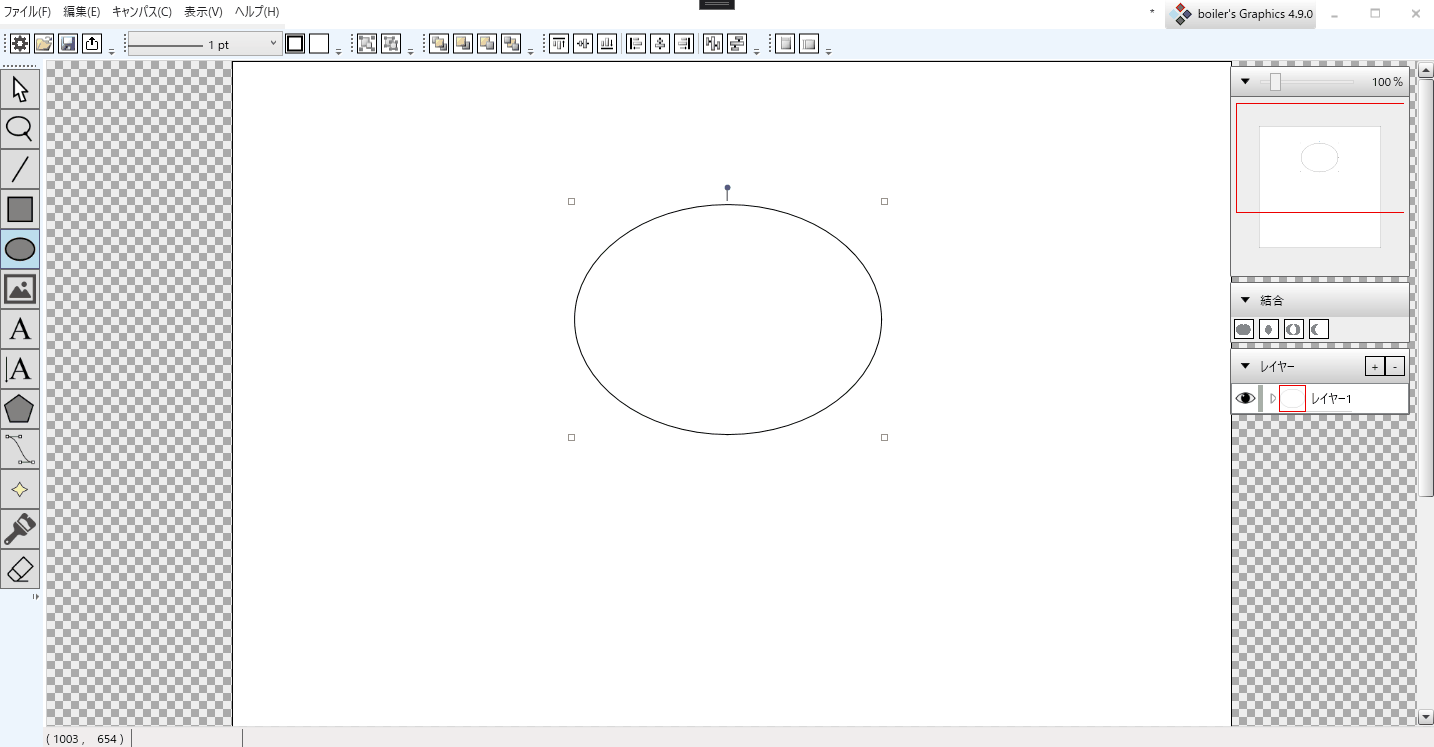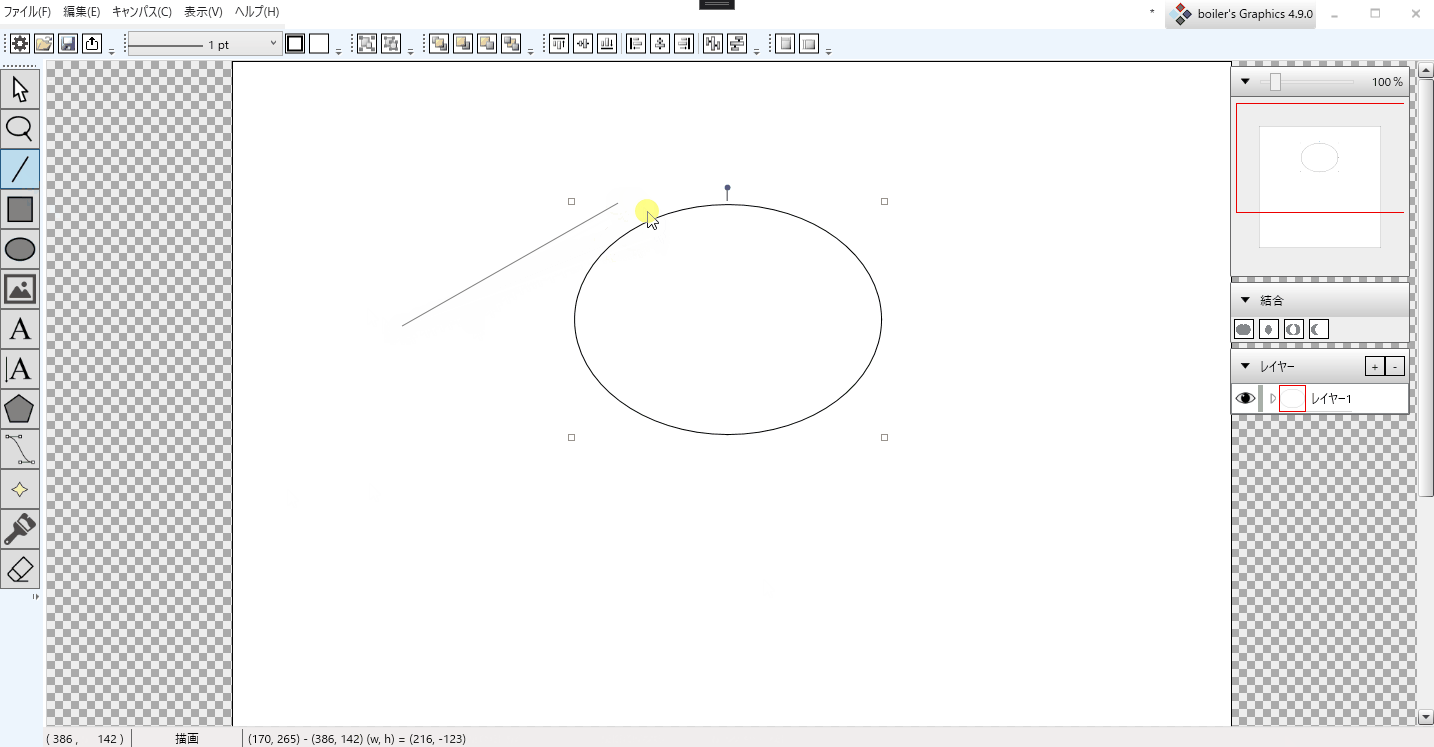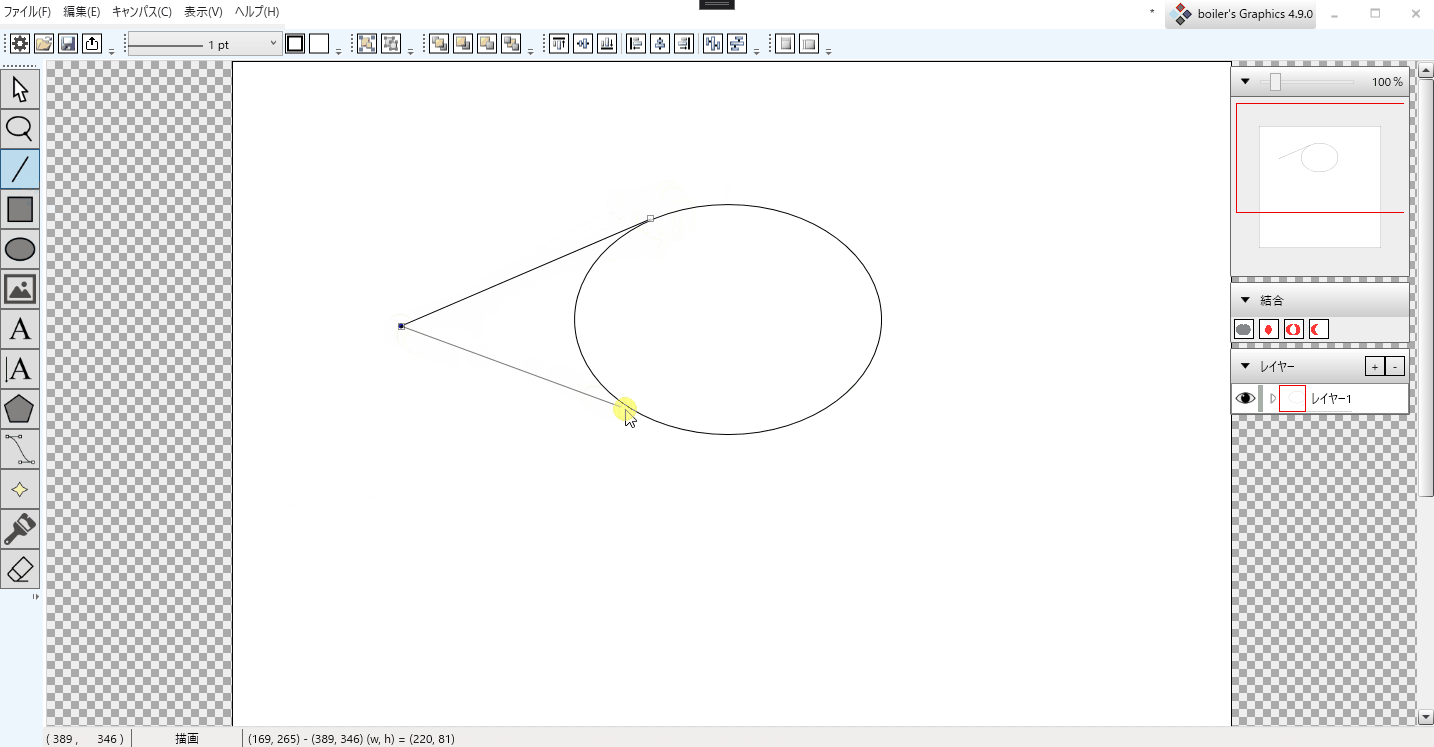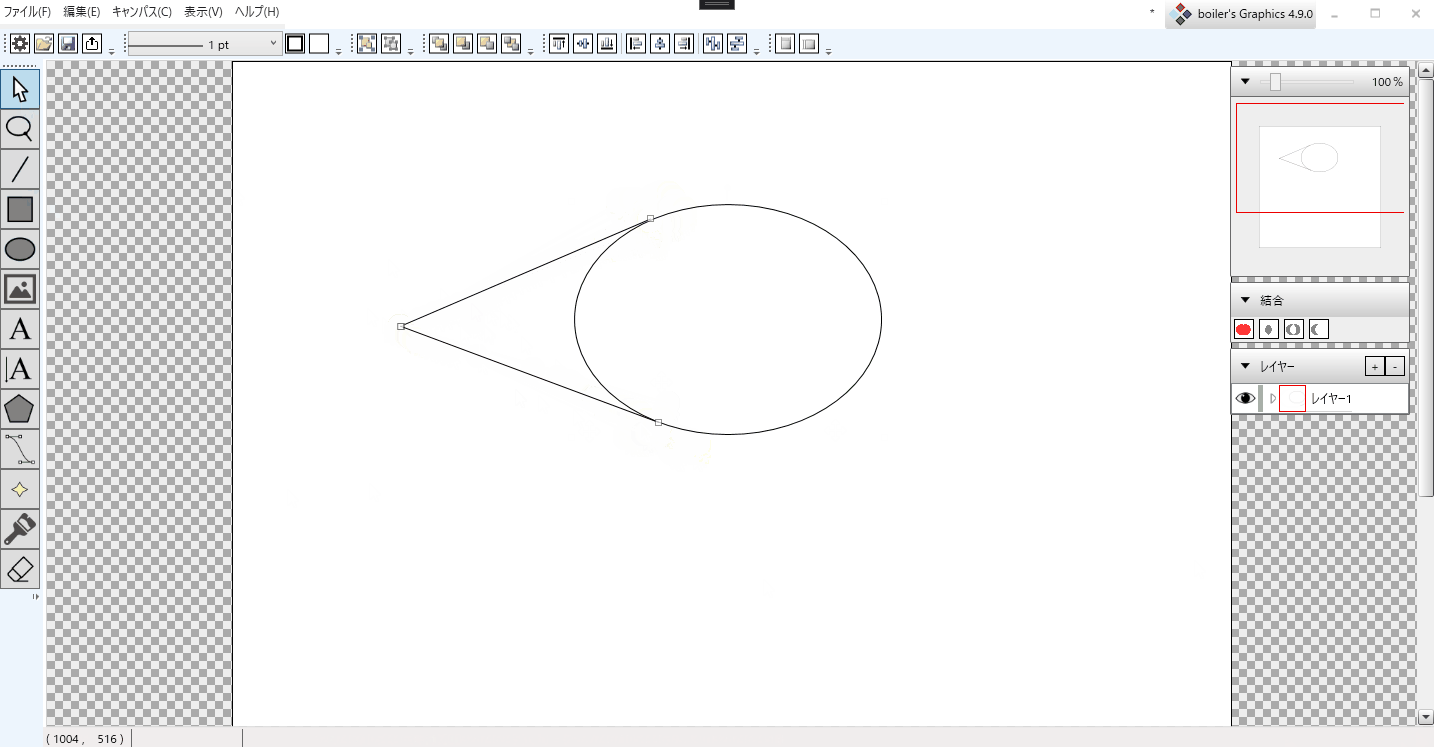
今、boiler's Graphicsで、描画した楕円の接線の交点をスナップするように実装しました。
この記事、Calculate where a line segment and an ellipse intersect in C#を参考に、以下のように楕円の接線の交点を求めるコードを書きました。記事のコードを少しアレンジしており、戻り値をTupleにしています。TupleのItem1は交点の配列、Item2は判別式の値です。パラメータはellipseが楕円のビューモデルで、pt1が線分の開始点、pt2が線分の終了点、segment_onlyは理解できていません!
using boilersGraphics.ViewModels;
using NLog;
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows;
namespace boilersGraphics.Helpers
{
public static class Intersection
{
/// <summary>
/// http://csharphelper.com/blog/2017/08/calculate-where-a-line-segment-and-an-ellipse-intersect-in-c/
/// </summary>
/// <param name="ellipse">ellipse</param>
/// <param name="pt1">beginPoint of tangent</param>
/// <param name="pt2">endPoint of tangent</param>
/// <param name="segment_only"></param>
/// <returns></returns>
public static Tuple<Point[], double> FindEllipseSegmentIntersections(NEllipseViewModel ellipse, Point pt1, Point pt2, bool segment_only)
{
var clone = ellipse.Clone() as NEllipseViewModel;
// If the ellipse or line segment are empty, return no intersections.
if ((clone.Width.Value == 0) || (clone.Height.Value == 0) ||
((pt1.X == pt2.X) && (pt1.Y == pt2.Y)))
return new Tuple<Point[], double>(new Point[] { }, double.NaN);
// Make sure the rectangle has non-negative width and height.
if (clone.Width.Value < 0)
{
clone.Left.Value = clone.Right.Value;
clone.Width.Value = -clone.Width.Value;
}
if (clone.Height.Value < 0)
{
clone.Top.Value = clone.Bottom.Value;
clone.Height.Value = -clone.Height.Value;
}
// Translate so the ellipse is centered at the origin.
double cx = clone.CenterX.Value;
double cy = clone.CenterY.Value;
clone.Left.Value -= cx;
clone.Top.Value -= cy;
pt1.X -= cx;
pt1.Y -= cy;
pt2.X -= cx;
pt2.Y -= cy;
// Get the semimajor and semiminor axes.
double a = clone.Width.Value / 2;
double b = clone.Height.Value / 2;
// Calculate the quadratic parameters.
double A = (pt2.X - pt1.X) * (pt2.X - pt1.X) / a / a +
(pt2.Y - pt1.Y) * (pt2.Y - pt1.Y) / b / b;
double B = 2 * pt1.X * (pt2.X - pt1.X) / a / a +
2 * pt1.Y * (pt2.Y - pt1.Y) / b / b;
double C = pt1.X * pt1.X / a / a + pt1.Y * pt1.Y / b / b - 1;
// Make a list of t values.
List<double> t_values = new List<double>();
// Calculate the discriminant.
double discriminant = B * B - 4 * A * C;
LogManager.GetCurrentClassLogger().Debug($"discriminant:{discriminant}");
if (Math.Abs(discriminant) < 0.1)
{
// One real solution.
t_values.Add(-B / 2 / A);
}
else if (discriminant > 0)
{
// Two real solutions.
t_values.Add((double)((-B + Math.Sqrt(discriminant)) / 2 / A));
t_values.Add((double)((-B - Math.Sqrt(discriminant)) / 2 / A));
}
// Convert the t values into points.
List<Point> points = new List<Point>();
foreach (double t in t_values)
{
// If the points are on the segment (or we
// don't care if they are), add them to the list.
if (!segment_only || ((t >= 0f) && (t <= 1f)))
{
double x = pt1.X + (pt2.X - pt1.X) * t + cx;
double y = pt1.Y + (pt2.Y - pt1.Y) * t + cy;
points.Add(new Point(x, y));
}
}
// Return the points.
return new Tuple<Point[], double>(points.ToArray(), discriminant);
}
}
}
これで普通の回転していない楕円の接線の交点は求めることができたのですが、回転した楕円にはまだ対応できていません。
例えば、45°回転した楕円の接線の交点を求めるにはどのようにしたらいいでしょうか?
高校数学なのか大学数学なのか、その区別もついておりませんが、わかる方いらっしゃいましたら、是非回答お願いします!!!
該当するソースコード
ブランチ:feature/intersection