E資格合格に向けて 深層学習day4 （強化学習、AlphaGo）

#強化学習とは
長期的に報酬を最大化できるように環境のなかで行動を選択できるエージェントを作ることを目標とする機会学習の一分野。強化学習の難しさは、状態を如何に表現できるか、そしてその状態に基づいていかに（現実的な時間内で）行動に結びつけることができるかというところにある。強化学習にも冬の時代があったが、Ｑ学習と関数近似法を組み合わせることで精度が向上し、利用されるようになる。

　Ｑ学習：行動価値関数を、行動する毎に更新することにより学習を進める方法
　関数近似法：価値関数や方策関数を関数近似する手法のこと

強化学習のイメージ

★強化学習にとって大事な関数
【方策関数】
　方策ベースの強化学習手法において、ある状態でどのような行動を採るのかの確率を与える関数

【価値関数】
　状態価値関数：ある状態の価値に注目する場合
　行動価値関数：状態と価値を組み合わせた価値に注目する場合

★方策勾配法
　方策関数を学習する手法。方策をモデル化して最適化する。
　

　※報酬を最大化するθを求める。勾配降下法と似ており、θは勾配降下法では重みにあたる。
　　J（θ）は期待収益（ＮＮでは誤差関数にあたる）。期待収益は出来るだけ大きくしたい。
　　そのため、前回のθから＋をしている。

【実装例】OpenAI Gym ~CartPole

# gymのインストール
pip install gym[all]
# coding: utf-8
import gym  # gymとNumPyのインポート。
import numpy as np

env = gym.make('CartPole-v0') # 環境に相当するオブジェクトをenvとおく。

goal_average_steps = 195 # 195ステップ連続でポールが倒れないことを目指す
max_number_of_steps = 200 # 最大ステップ数
num_consecutive_iterations = 100 # 評価の範囲のエピソード数
num_episodes = 5000
last_time_steps = np.zeros(num_consecutive_iterations)

# 価値関数の値を保存するテーブルを作成する。
# np.random.uniformは指定された範囲での一様乱数を返す。
q_table = np.random.uniform(low=-1, high=1, size=(4**4, env.action_space.n))

def bins(clip_min, clip_max, num):
    return np.linspace(clip_min, clip_max, num + 1)[1:-1]
    # np.linspaceは指定された範囲における等間隔数列を返す。

def digitize_state(observation):
    # 各値を４個の離散値に変換
    # np.digitizeは与えられた値をbinsで指定した基数に当てはめる関数。インデックスを返す。
    cart_pos, cart_v, pole_angle, pole_v = observation
    digitized = [np.digitize(cart_pos, bins=bins(-2.4, 2.4, 4)),
                 np.digitize(cart_v, bins = bins(-3.0, 3.0, 4)),
                 np.digitize(pole_angle, bins=bins(-0.5, 0.5, 4)),
                 np.digitize(pole_v, bins=bins(-2.0, 2.0, 4))]

    # 0~255に変換
    return sum([x* (4**i) for i, x in enumerate(digitized)]) # インデックス付きループをすることができる。


def get_action(state, action, observation, reward, episode):
    next_state = digitize_state(observation)
    epsilon = 0.5 * (0.99** episode)
    if epsilon <= np.random.uniform(0, 1): # もし一様乱数のほうが大きければ
        next_action = np.argmax(q_table[next_state])# q_tableの中で次に取りうる行動の中で最も価値の高いものを
                                                    # next_actionに格納する
    else:# そうでなければ20%の確率でランダムな行動を取る
        next_action = np.random.choice([0, 1])


    # Qテーブルの更新
    alpha = 0.2
    gamma = 0.99
    q_table[state, action] = (1 - alpha) * q_table[state, action] + \
            alpha * (reward + gamma * q_table[next_state, next_action])
    return next_action, next_state

step_list = []
for episode in range(num_episodes):
    # 環境の初期化
    observation = env.reset()

    state = digitize_state(observation)
    action = np.argmax(q_table[state])

    episode_reward = 0
    for t in range(max_number_of_steps):
        env.render() # CartPoleの描画

        observation, reward, done, info = env.step(action) # actionを取ったときの環境、報酬、状態が終わったかどうか、デバッグに有益な情報

        if done: # 倒れた時罰則を追加する
            reward -= 200
        # 行動の選択
        action, state = get_action(state, action, observation, reward, episode)
        episode_reward += reward


        if done:
            print('%d Episode finished after %f time steps / mean %f' %
                (episode, t + 1, last_time_steps.mean()))
            last_time_steps = np.hstack((last_time_steps[1:], [t+1]))
            # 継続したステップ数をステップのリストの最後に加える。np.hstack関数は配列をつなげる関数。
            step_list.append(t+1)
            break

    if (last_time_steps.mean() >= goal_average_steps): # 直近の100エピソードの平均が195以上であれば成功
        print('Episode %d train agent successfully!' % episode)
        break

# 以下のコードでグラフを表示
import matplotlib.pyplot as plt
plt.plot(np.arange(len(step_list)), step_list)
plt.xlabel('episode')
plt.ylabel('max_step')

実装結果

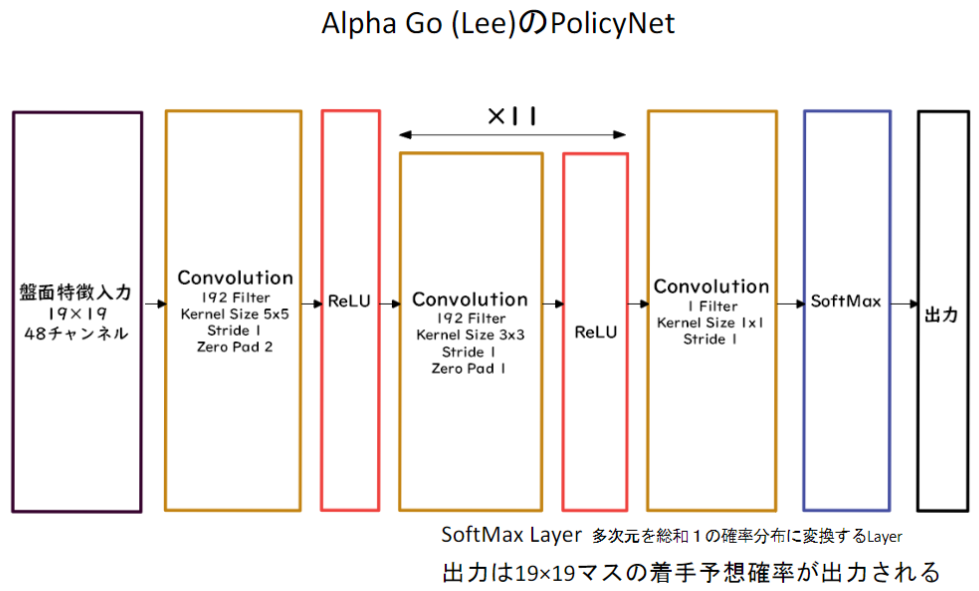
#AlphaGo
2015～2017年にかけてDeepMind社が開発したAlphaGo（アルファ碁）という碁のプログラムが、当時の世界チャンピオ級の棋士を次々と打ち破っていく。AlphaGoも状態や行動の評価にＣＮＮを用いている。また実際にどのような手を打つべきかの探索にはモンテカルロ木探索が用いられている。

【AlphaGo（Lee）の方策関数】

【AlphaGo（Lee）の価値関数】

【AlphaGoの学習ステップ】
ポイントは、いきなり強化学習をするのではなく、まずは教師あり学習にてプロ棋士の打ち手を学ぶ。その上で、強化学習を行っていること。

【AlphaGo Zero】
AlphaGo（Lee）との違い
1.教師あり学習を一切行わず、強化学習のみで作成
2.特徴入力からヒューリスティックな要素を排除し、石の配置のみにした
3.PolicyNetとValueNetを1つのネットワークに統合した
4.Residual Netを導入した
5.モンテカルロ木探索からRollOutシミュレーションをなくした

Residual Network
ネットワークにショートカット構造を追加して、勾配爆発・消失を抑える効果を狙ったもの。これにより、100層を越えるネットワークでの安定した学習が可能となった

【実装例】Residual Network

import pytorch.nn as nn
class Block(nn.Module):
    def __init__(self, channel_in, channel_out):
        super().__init__()
        channel = channel_out // 4
        # 1x1 の畳み込み
        self.conv1 = nn.Conv2d(channel_in, channel,
                               kernel_size=(1, 1))
        self.bn1 = nn.BatchNorm2d(channel)
        self.relu1 = nn.ReLU()
        # 3x3 の畳み込み
        self.conv2 = nn.Conv2d(channel, channel,
                               kernel_size=(3, 3),
                               padding=1)
        self.bn2 = nn.BatchNorm2d(channel)
        self.relu2 = nn.ReLU()
        # 1x1 の畳み込み
        self.conv3 = nn.Conv2d(channel, channel_out,
                               kernel_size=(1, 1),
                               padding=0)
        self.bn3 = nn.BatchNorm2d(channel_out)
        # skip connection用のチャネル数調整        
        self.shortcut = self._shortcut(channel_in, channel_out)
        
        self.relu3 = nn.ReLU()
    def forward(self, x):
        h = self.conv1(x)
        h = self.bn1(h)
        h = self.relu1(h)
        h = self.conv2(h)
        h = self.bn2(h)
        h = self.relu2(h)
        h = self.conv3(h)
        h = self.bn3(h)
        shortcut = self.shortcut(x)
        y = self.relu3(h + shortcut)  # skip connection
        return y
    def _shortcut(self, channel_in, channel_out):
        if channel_in != channel_out:
            return self._projection(channel_in, channel_out)
        else:
            return lambda x: x
    def _projection(self, channel_in, channel_out):
        return nn.Conv2d(channel_in, channel_out,
                         kernel_size=(1, 1),
                         padding=0)