はじめに
はじめまして、NTTドコモ R&D Advent Calendar 2020の10日目の記事を担当いたします、廣川です!
業務では,マーケティング分野を中心にデータ分析に取り組んでいます。私は、クラスタリングに縁があるようで、気がつくと様々なデータに対するクラスタリング手法を学んでいました。そこで本記事では,それらのクラスタリング手法についてご紹介したいと思います!
本記事の目的
- 行列・グラフ・時系列データに対するクラスタリング手法をご紹介します。
- クラスタ数の決め方や評価指標などについても簡単にご紹介します。
ご紹介する手法
ソースコードあり
- 行列:Latent dirichlet allocation (LDA).
- グラフ:Spectral clustering, Clauset-Newman-Moore greedy modularity maximization, Louvain method.
- 時系列:Hidden Markov model (HMM).
概要のみ
- 行列:Non-negative matrix factorization (NMF).
- グラフ:A structural clustering algorithm for networks (SCAN).
- 時系列:Dynamic time warping (DTW), Toeplitz Inverse Covariance-Based Clustering of Multivariate Time Series Data(TICC).
評価指標(ソースコードあり)
- ラベルあり:Adjusted mutual information (AMI)
- 自然言語処理:Perplexity, Coherence.
- グラフ:Modularity, Conductance.
- 確率モデル:Bayesian information criterion (BIC), log likelihood.
クラスタリングとは?
クラスタリングは、教師なし学習と呼ばれる手法の1つで、大規模なデータを少数のグループにまとめる手法です。主な用途としては、解釈性の向上やそれに伴うインサイトの獲得(データマイニング)。また、計算リソースの削減や計算モデルが扱いやすくすること(次元削減・特徴量抽出)等があげられます。
最近は、次元削減や特徴量抽出の用途としては、分散表現が用いられることも多いと思いますが、それでも、クイックな分析が求められるケースや、手元にある計算リソースの関係などで、クラスタリング手法が用いられるケースもあります。
教師あり学習と比較すると、教師ラベルがなくても分析が可能という大きなメリットがあります。一方で、正解データがないことから、何をもって「よいクラスタ」や「よい手法」とするのか?という評価が難しい点がデメリットとして考えられます。このような背景から、よく使われるクラスタリングの評価指標についても簡単にご紹介していきます。
行列データのクラスタリング
それでは、まず行列データのクラスタリングから見ていきましょう!
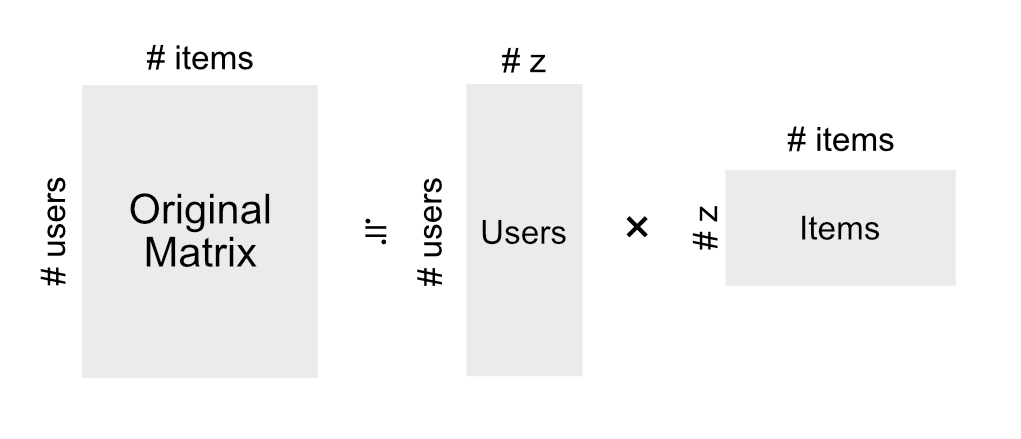
行列データのクラスタリングというと、トピックモデルと、行列因子分解(Matrix Factorization)が有名です。両者とも同様の問題設定となっており、大きな行列を2つの小さな行列に分解する手法と考えることができます1。
トピックモデルは自然言語処理の分野で用いられてきた手法で、単語と文章の共起関係に基づきクラスタリングを行います。Pythonですぐに使えるトピックモデルとしては、Latent Dirichlet Allocation (LDA)や、LDAのトピック生成部分を階層化することで、クラスタ数も同時に学習できるようなになったHDP−LDAがあります。
もう一方の行列因子分解は、協調フィルタリングというレコメンドシステムの用途として有名になった手法です。また、次元削減後に、元の行列を復元することで、欠損値補間の用途として利用されることもあります。こちらもPythonの利用と、マーケティング分野などでの応用を考えると、非負制約を追加したNon-negative Matrix Factorizationが扱いやすいと思います。
このように、異なるバックグラウンドから生まれた2つの手法ですが、実はこの2つの手法はかなり似ているようです。厳密には、LDAのベイズ化前であるpLSAと一般化KLダイバージェンス基準のNMFは等価です。
今回は、scikit-learnにある20 newsgroups datasetを用いて、LDAのデモンストレーションを行いたいと思います。
LDAによるクラスタリング
import pandas as pd
import gensim
from gensim.utils import simple_preprocess
from gensim.parsing.preprocessing import STOPWORDS
from gensim import corpora
from gensim.corpora.dictionary import Dictionary
from gensim.models.ldamodel import LdaModel
from nltk.stem import WordNetLemmatizer, SnowballStemmer
from nltk.stem.porter import *
import numpy as np
import nltk
from sklearn.datasets import fetch_20newsgroups
from sklearn.metrics import adjusted_mutual_info_score
np.random.seed(2020)
nltk.download('wordnet')
stemmer = SnowballStemmer('english')
データの読み込み
dataset = fetch_20newsgroups(shuffle=True, random_state=32, remove=('headers', 'footers', 'qutes'))
documents = pd.DataFrame({'News': dataset.data, 'Target': dataset.target})
print(documents.shape)
documents.head()
# (11314, 2)
前処理
前処理は、こちらが非常にわかりやすかったため、ほぼそのまま利用させてもらっています。
行った前処理は、以下の内容です。
- ドキュメントのトークン化:具体的には,テキストを文単位に,文を単語単位にそれぞれ分割します.大文字の単語を小文字に修正し,句読点を取り除きます.
- 3文字未満の単語の除去
- ストップワードの除去:ストップワードとは,頻出あるいは一般的すぎて,利用価値が低いと考えられる単語のことをいいます.ex. the, a, for
- 単語を見出し語化 (lemmatize) :具体的には,三人称の単語は一人称に,過去時制及び未来時制の動詞は現在時制に変更されます.
- 単語の語幹抽出 (stemming)
def lemmatize_stemming(text):
return stemmer.stem(WordNetLemmatizer().lemmatize(text, pos='v'))
def preprocess(text):
result = []
for token in gensim.utils.simple_preprocess(text):
if token not in gensim.parsing.preprocessing.STOPWORDS and len(token) > 3:
result.append(lemmatize_stemming(token))
return result
# 前処理のテスト
# 適当な文で前処理の前後を比較
doc_sample = documents.iloc[0].News
words = []
for word in doc_sample.split(' '):
words.append(word)
print('original document: ')
print(words)
print('\n\ntokenized and lemmatized document: ')
print(preprocess(doc_sample))
# original document:
# ['Please', 'could', 'someone', 'in', 'the', 'US', 'give', 'me', 'the', 'current', 'street', '\nprices', 'on', 'the', 'following,', 'with', 'and', 'without', 'any', 'relevant', 'taxes:\n\n', '8', 'Mb', '72', 'pin', 'SIMM\n16', 'Mb', '72', 'pin', 'SIMM', '(both', 'for', 'Mac', 'LC', 'III)\n\nAre', 'any', 'tax', 'refunds', 'possible', 'if', 'they', 'are', 'to', 'be', 'exported\nto', 'the', 'UK?', 'Can', 'you', 'recommend', 'a', 'reliable', 'supplier?']
# tokenized and lemmatized document:
# ['current', 'street', 'price', 'follow', 'relev', 'tax', 'simm', 'simm', 'refund', 'possibl', 'export', 'recommend', 'reliabl', 'supplier']
# すべてのデータに適用
processed_documents = documents['News'].map(preprocess)
processed_documents[:10]
前処理後の文章が、シンプルな単語(語幹)の集合になっていることがわかります。最後に、全データに前処理を適用しています。
次に、データを学習用とテスト用に分けます。
# データサイズの確認
len(processed_documents)
# 11314
# 学習用データとテスト用データに分ける
# すでにシャッフル済みのため、そのまま利用する
train_set = processed_documents[:10000]
test_set = processed_documents[10000:]
print(len(train_set), len(test_set))
# 10000 1314
# LDA用にフォーマットを整理する
dictionary = gensim.corpora.Dictionary(processed_documents)
dictionary.filter_extremes(no_below=15, no_above=0.5, keep_n=100000)
train_corpus = [dictionary.doc2bow(doc) for doc in train_set]
test_corpus = [dictionary.doc2bow(doc) for doc in test_set]
クラスタ数の決定
クラスタ数の決定は、応用上よく遭遇する問題だと思います。あくまで私の経験ですが、以下のように決めることが多いです。
- 今回の問題のように事前知識からクラスタ数の目安がある
- いくつかのクラスタ数で実験し定性評価で決定
- クラスタ数まで最適化するモデルを利用する(HDP-LDA等)
- 目的が別にある場合(予測タスクなど)、それに基づくCross Validation
- 確率モデルならBIC等の情報量規準を利用する
クイックな案件やデータの概要をつかみたいような探索的なモチベーションの場合は、1.や2.を使うこともあります。一方で、論文を書く場合など客観性が求められる場合は、3.〜5.のうち適用可能なものを選択しています。
今回は、正しいクラスタ数(20)が与えられていることから、こちらを利用したいと思います。参考として、クラスタ数が10、30のときの振る舞いも確認します。
それでは、クラスタ数を10、20、30でLDAを実行します。
lda_10 = gensim.models.LdaMulticore(train_corpus, num_topics=10, id2word=dictionary, passes=2, workers=2)
lda_20 = gensim.models.LdaMulticore(train_corpus, num_topics=20, id2word=dictionary, passes=2, workers=2)
lda_30 = gensim.models.LdaMulticore(train_corpus, num_topics=30, id2word=dictionary, passes=2, workers=2)
AMIとPerplexity/Coherenceによる定量評価
クラスタリング手法の評価をする場合、教師ラベルがないことから、データとの類似度を指標とすることが一般的です。また、クラスタの利用目的がはっきりしている場合には、その目的やタスクに合わせた独自の指標が定義されることもあります。具体例としては、トピックモデルをトピック品質の観点から評価するCoherence等が該当します。
今回は、正解データ(20のラベルデータ)が存在することとから、Adjusted Mutual Information(AMI)によって評価します。また参考として、トピックモデルの評価指標としてよく利用されるPerplexityとCoherenceも見てみます。
このAMIという指標は、簡単に言うと教師あり学習の評価で利用するAccuracyのようなものです2。 ただし、クラスタリングの場合には、教師あり学習とは異なり、同じクラスタ割当をしていたとしてもラベルが異なることがあり得ます。例えば、以下の2つの割当を考えます。
- Aさん/Bさん/Cさんをクラスタ1、Dさん/Eさんをクラスタ2とする割当
- Aさん/Bさん/Cさんをクラスタ2、Dさん/Eさんをクラスタ1とする割当
この2つは、クラスタリング結果としては等価ですが、ラベルが異なっています。そのため、通常のAccuracyで評価すると、性能が本来よりも低く見積もられてしまいます。そこで、ラベルを無視し、純粋に割当のみを評価する指標がAMIです。具体的には、異なる割当の時ほど、値が0に近く、この例のように全く等価の場合、1を示します。
それでは、LDAの結果を見てみましょう。
# AMIによる定量評価
dist = lda_20.get_document_topics(test_corpus)
clusters = [max(lis,key=lambda item:item[1])[0] for lis in dist]
print(f"{adjusted_mutual_info_score(clusters, documents[10000:].Target):.3f}")
# 0.377
AMIが高くないことから、正解ラベルの意図するようなクラスタ割当になっていない可能性が高いです。今回のように求める割当がはっきりしているケースで、教師データや特徴量も潤沢にあるのであれば、教師あり学習を用いる方がよいかもしれません。一方で、教師データが少ない場合には、モデルの改良(ハイパーパラメータの調整や制約の追加など)によって、目的のラベルに近づけることができるかもしれません。
今回の目的は、あくまでデータに対する探索的なアプローチなので、これ以降は教師データがない状況を想定して分析を続けます。
次に、クラスタ数を10、20、30と変化させた際のPerplexityとCoherenceの変化を見てみます。Coherenceには、複数の種類がありますが、今回は、対象データのコーパスのみから算出可能なU-mass Coherenceを用いています。
# perplexity
perplexity = np.exp2(-lda_20.log_perplexity(test_corpus))
print(f'Perplexity score: {perplexity:.2f}')
# coherence(u-mass)
cm = gensim.models.CoherenceModel(lda_20,corpus=test_corpus,dictionary=dictionary,coherence='u_mass')
print(f'u_mass coherence score: {cm.get_coherence():.2f}')
# perplexity score: 590.84
# u_mass coherence score: -2.61
| #clusters | Perplexity | Coherence |
|---|---|---|
| 10 | 352.53 | -1.99 |
| 20 | 590.83 | -2.62 |
| 30 | 1256.94 | -2.25 |
あくまで1回の実験結果ですが、PerplexityやCoherenceの観点からは、クラスタ数:10が良さそうです。
トピックの上位単語による定性評価
最後に定性的な分析を行います。定性的な分析(解釈)には、それなりの時間と労力がかかることから、私は何かしらの定量的な指標でモデルの性能を評価してから、定性評価(解釈)することにしています。その方が、手戻りが少なくなることに加え、その結果が「新発見なのか?」「何かのミスなのか?」というところを悩むコストが低減されるためです。
それでは、各トピックの上位単語を可視化してみましょう!
※クラスタ数は10のものを可視化します。
for idx, topic in lda_10.print_topics(-1, num_words=5):
print('Topic {}: {}'.format(idx, topic))
# Cluster 0: 0.008*"know" + 0.008*"peopl" + 0.006*"like" + 0.005*"think" + 0.005*"time"
# Cluster 1: 0.011*"drive" + 0.011*"articl" + 0.010*"like" + 0.008*"know" + 0.006*"think"
# Cluster 2: 0.011*"space" + 0.007*"articl" + 0.007*"launch" + 0.006*"nasa" + 0.006*"like"
# Cluster 3: 0.012*"game" + 0.008*"articl" + 0.008*"team" + 0.007*"window" + 0.007*"year"
# Cluster 4: 0.009*"peopl" + 0.007*"right" + 0.007*"christian" + 0.007*"believ" + 0.007*"articl"
# Cluster 5: 0.011*"file" + 0.010*"window" + 0.007*"program" + 0.006*"articl" + 0.006*"like"
# Cluster 6: 0.007*"like" + 0.007*"articl" + 0.007*"year" + 0.007*"good" + 0.006*"know"
# Cluster 7: 0.010*"think" + 0.009*"articl" + 0.008*"time" + 0.007*"know" + 0.007*"say"
# Cluster 8: 0.013*"articl" + 0.006*"time" + 0.005*"orbit" + 0.005*"think" + 0.005*"like"
# Cluster 9: 0.011*"peopl" + 0.010*"armenian" + 0.007*"say" + 0.006*"know" + 0.006*"think"
少しだけ中身を見てみます。今回のクラスタ2はspaceやlaunch、nasa等の宇宙系のクラスタのように見えます。また、クラスタ5は、file, window, programとありますので、コンピュータ系のクラスタのようです。このように、教師データがなくても、クラスタ数や各クラスタの特徴など、ある程度データの特徴が判明しました。
グラフデータのクラスタリング
それでは続いて、最近のトレンドであるグラフデータについて、クラスタリングの観点から見てみましょう!
まず、グラフデータのクラスタリングを、以下のように整理してみます。どちらも出力されるのはNodeのコミュニティ(集合)であり、Linkの集合ではありません。
- Nodeベースのクラスタリング
- Linkベースのクラスタリング
Nodeベースのクラスタリングでは、A Structural Clustering Algorithm for Networks(SCAN)と呼ばれるアルゴリズムがあります。こちらは2つのNode間でどれだけ同じNodeに隣接しているかという指標(Structural Similarity)に基づきクラスタリングを行います。
Linkベースのクラスタリングは、スペクトラルクラスタリング(Normalized cut等)や、コミュニティ検出(モジュラリティベースの手法など)等が存在します。特に、コミュニティ検出と呼ばれるアルゴリズムでは、自動でクラスタ数が定まるという特徴があります。 例えば、モジュラリティに基づくクラスタリング手法では、以下のモジュラリティという量を最大化する問題を考えます。
Q=\sum_{l \in C}(e_{ll}-a_l^2)\\
e_{lm} = \frac{1}{2M}\sum_{i \in V_l}\sum_{j \in V_m} A(i,j)\\
a_l = \sum_{m \in C} e_{lm} = \frac{1}{2M}\sum_{i \in V_l}\sum_{j \in V}A(i,j)
ここで、$C$は検出したいコミュニティの集合であり、$i,j$はNode、$M$はLinkの総数、$V_l, V_m$はコミュニティ$l, m$に含まれるNode集合、$A(i,j)$は対象グラフの隣接行列を表します。また、$e_{lm}$はコミュニティ$l, m$間に存在するLinkの割合、$a_l$はコミュニティ$l$内のNodeに接続するLink数の割合を表します。
この指標は定性的には、同じクラスタに所属するすべてのLinkに対して、ランダムグラフで期待されるものより、どれだけ多くのLinkが存在しているかを評価しています。先にも述べましたが、この手法では、クラスタ集合Cを含めて最適化されるため、ユーザがクラスタ数を指定する必要はありません。
Modularityによるコミュニティ検出
それでは、Modularityによるコミュニティ検出の実験を行います。具体的には、Louvain methodと呼ばれる手法と、Clauset-Newman-Moore greedy modularity maximizationという手法を用いてコミュニティ検出を行います。
Louvain methodの方が高速・高精度な手法として有名です。Greedy modularity maximizationの方は、今回のグラフのサイズでは問題なく動作しますが、もう少し大きくなると計算負荷が高くなる印象です。
今回は、Stochastic Block modelという手法で人工的にデータを生成します3。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.cm as cm
from collections import defaultdict
import networkx as nx
from networkx.algorithms.community import greedy_modularity_communities
from sklearn.cluster import SpectralClustering
from cdlib import algorithms
from networkx.algorithms.cuts import conductance
可視化用の関数を定義
def show_graph(g, node2community=None, k=0.1):
"""\
可視化用の関数
Parameters
----------
g : Graph
対象のグラフ
node2community : dict
Node IDとコミュニティIDの辞書
k : float
可視化パラメータ
"""
plt.figure(figsize=(10, 8))
pos = nx.spring_layout(g, k=k)
# コミュニティを指定したとき
if node2community is not None:
cmap = cm.get_cmap('viridis', max(node2community.values()) + 1)
nx.draw_networkx_nodes(g, pos, node2community.keys(), node_size=40,
cmap=cmap, node_color=list(node2community.values()))
else:
nx.draw_networkx_nodes(g, pos, node_size=40)
nx.draw_networkx_edges(g, pos, alpha=0.5)
plt.axis('off')
plt.show()
Stochastic Block modelによるグラフ生成と可視化
# パラメータ設定
## 対角成分(クラスタ内)を密に、他を疎にしています。
sizes = [75, 100, 300]
probs = [
[0.1, 0.001, 0.002],
[0.001, 0.2, 0.004],
[0.002, 0.004, 0.5]
]
g = nx.stochastic_block_model(sizes, probs, seed=0)
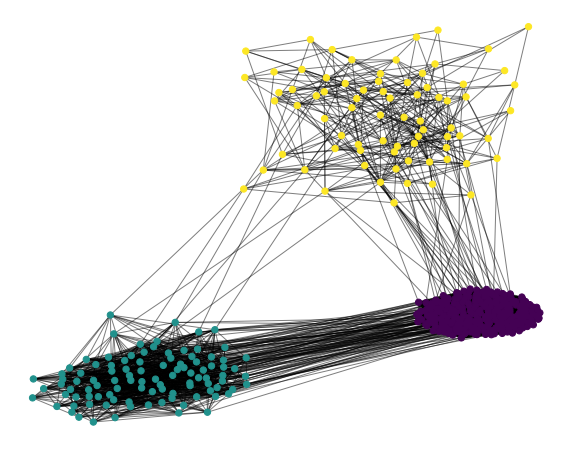
# 可視化
show_graph(g, k=0.1)
Modularityによるコミュニティ検出を実行します(Greedy modularity maximization)。
community = list(greedy_modularity_communities(g))
print("コミュニティ数: ", len(community))
print("コミュニティラベル: ", list(range(len(community))))
# コミュニティ数: 3
# コミュニティラベル: [0, 1, 2]
コミュニティ数を設定せずに、きちんと3つのクラスタが検出されたことがわかります!
続いて、Louvain methodによるコミュニティ検出を実行します。
com = algorithms.louvain(g, weight='weight', resolution=1., randomize=True)
node2community = com.to_node_community_map()
node2community = {k:v[0] for k, v in node2community.items()}
community = defaultdict(list)
for i in range(len(node2community)):
community[node2community[i]].append(i)
community = community.values()
print("コミュニティ数: ", len(community))
print("コミュニティラベル: ", list(range(len(community))))
# コミュニティ数: 5
# コミュニティラベル: [0, 1, 2, 3, 4]
今度は、5つのコミュニティが検出されてしまいました。しかし、この結果は次のModularityを確認してみると、意外とよい結果であることがわかります。
ConductanceとModularityによる定量評価
先ほどのモジュラリティだけでなく、グラフクラスタリングの評価指標としてよく使われるコンダクタンスも算出します。コンダクタンスは、Ncutに似た指標ですが、物理学をバックグラウンドにもつ指標です。具体的には、あるクラスタの頂点集合$C_i$のコンダクタンス$\phi(C_i)$は、以下のように定義されます。
\phi(C_i) = \frac{\sum_{i \in C_i}\sum_{j \notin C_i}A(i,j)}{min(\kappa_i, \overline{\kappa_i})}
ここで、$A(i,j)$は隣接行列、$\kappa_i, \overline{\kappa_i}$は、それぞれ、頂点集合$C_i$内、それ以外の頂点集合$\overline{C_i}$内の次数の和です。
そしてグラフ全体のコンダクタンス$\phi(G)$は、すべてのクラスタ(頂点集合)のコンダクタンスの最小値として定義されます。
\phi(G) = min_{C_i}(\phi(C_i))
Pythonコードとしては、下記のようにすると算出できます。
for c in list(community.values()):
print(conductance(g, c))
print(f"modularity : ", modularity(g, community))
# conductance for 0: 0.06059465562664659 #<-最小値
# conductance for 1: 0.06469135802469136
# conductance for 2: 0.07278481012658228
# modularity : 0.09895468017762296
次に、比較対象として、Ncutのクラスタ数:2の場合と5の場合を作成します。コードとしては、クラスタ2のケースのみ記載します。
adjacency_matrix= nx.to_numpy_matrix(g)
num_community = 2
sc = SpectralClustering(num_community, affinity='precomputed', n_init=100, assign_labels='kmeans')
node2community = sc.fit_predict(adjacency_matrix)
# 可視化用
vis_node2community = {v : node2community[i] for i, v in enumerate(g.nodes)}
community = defaultdict(list)
for i in range(len(node2community)):
community[node2community[i]].append(i)
for c in list(community.values()):
print(conductance(g, c))
print(f"modularity : ", modularity(g, community))
# conductance for 0: 0.06059465562664659 <-最小値
# conductance for 1: 0.06059465562664659
# modularity : 0.09817090642685321
| Greedy | Louvain | Ncut:2 | Ncut:5 | |
|---|---|---|---|---|
| Conductance | 0.0606 | 0.0647 | 0.0606 | 0.0647 |
| Modularity | 0.0990 | 0.1044 | 0.0982 | 0.0935 |
グラフ全体のコンダクタンスとして、最小値を採用しているため、真のクラスタ数:3とは異なるクラスタ数:2のNcutでも、モジュラリティベースの手法と同じコンダクタンスの値となっています。この現象は、こちらでも指摘されており、評価指標としてコンダクタンスを利用する場合は、ご自身の目的に適合するかを確認するとよいかもしれません。
他方のModularityを見てみると、Louvain法が最大となっていることがわかります。今回は、3つのクラスタになるようにタスクを設定したつもりだったため、トイデータの生成方法や指標が厳密な意味で合わなかったと考えられます。一方で、先ほどの図を見ると、定性的には3つのクラスタがあるようにも見えると思います。あくまで個人的な考えですが、このような場合は、インサイトを得るためと割り切り(クラスタ数:3を採用し)、施策設計などでカバーできればよいのではないかと思っています。
可視化による定性評価
今回検出されたコミュニティ(GreedyとLouvainの結果)をNodeの色を変えて可視化してみます。
## フォーマットを整えて、再度クラスタを色分けして可視化
node2community = {}
for i in range(len(community)):
for n in community[i]:
node2community[n] = i
# 可視化
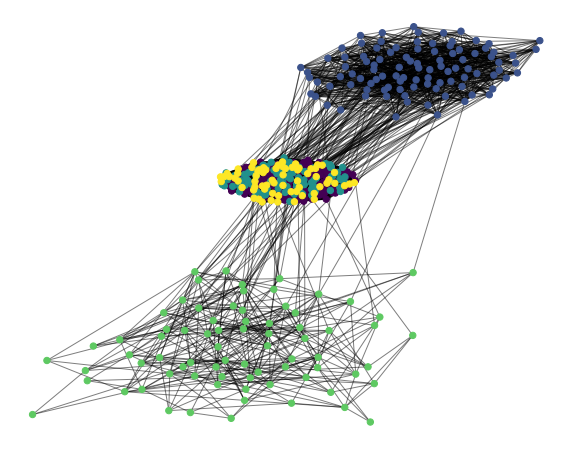
show_graph(g, node2community, k=0.1)
上図のGreedyの方の結果は、想定通り、3つの集団が検出されていることが定性的にも確認できました!下図のLouvainの方は、1つと想定していた真ん中のクラスタが複数に分割されていることがわかります。
時系列データのクラスタリング
最後に時系列データのクラスタリングについてご紹介いたします!
時系列データのクラスタリングは、大きく2つに分けられます。
- 時系列データ全体を1点として扱い、別の時系列との類似度を評価する whole time series clustering.
- 時系列データそのものを複数のセグメントに分割し、そのセグメントをクラスタリングするsubsequence time series (STS) clustering.
Whole time series (WTS) clusteringの代表的なものは、Dynamic Time Warping (DTW)と呼ばれる手法です。DTWは、まず、2つの時系列の各点間の距離を総当たりで計算します。次に、時系列のインデックスを表す2次元平面上で、最初のインデックス(0,0)から、それぞれの系列の最後のインデックス(N,M)までの経路を探索します。その際、重複を許容した上で距離の和が最小となるようにマッチングをとっていきます。
そのため、系列の長さが異なる場合でも適用可能であり、また、位相がずれていても、形状が似ている場合の類似度が高くなるという特徴があります。後者に関しては、時刻が重要な場合など、問題によって向き不向きがあると思いますので、適用の際は注意が必要です。
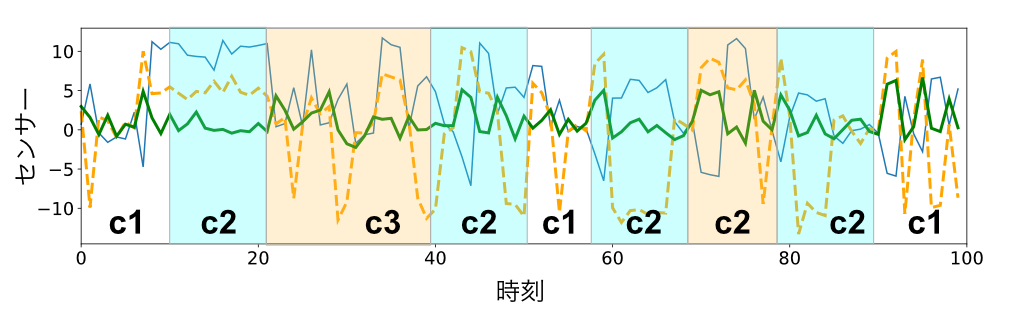
もう一つのSTS clusteringは、ユーザのセンサーデータを例に説明すると、WTS clusteringが、複数人の1日の行動や1週間の行動などに基づきユーザをクラスタリングするのに対し、STS clusteringは、ユーザ個人4の1日や1週間に基づき、時間帯をクラスタリングします。STS Clusteringのイメージ図を載せておきます(実際の結果ではありませんので値とクラスタラベルは無関係です)。
出力される結果に関しても、WTSでは、よく走るユーザ集合や、階段の上り降りが多いユーザ集合などであるのに対して、STSでは、朝と夜は走っている、お昼は階段が多い等の時間帯集合です。このようにSTS clusteringでは、時間帯という概念が残るため、解釈性を保った次元削減手法としても利用できます(朝と夜に走りやすく、お昼は階段が多いユーザ等)。
STS clusteringの有名な手法として、KDD2017のRunner upとなったToeplitz Inverse Covariance-Based Clustering of Multivariate Time Series Data(TICC)があげられます。
この手法は、まず、各データのクラスタラベルを初期化します。次に、ラベルごとにToeplitz graphical lassoという手法でスパースなMRFの構造を推定します。そして、時系列的な近傍で変化が起こりにくい(temporal consistency)という仮定のもと、尤度とこのペナルティ項に基づき、近傍の時系列のノイズを除去しながら、各時点のデータにクラスタ(MRF)を割り当てていきます。この2つの処理を収束するまで繰り返すことで、最終的にクラスタシークエンスと、各クラスタの構造(スパースなMRF)が推定されます。
ここで、MRFのPrecision matrix (共分散行列の逆行列)を、各センサーをNodeとするグラフとして考えてみます。このとき、もし2つのNode間にLinkが張られていないならば、この2つのNodeは条件付き独立となる性質があります。これは、他のすべてのセンサーの値で条件付けした際に、この2つセンサー値は互いに影響しないことを意味します。そのため、スパースなMRFが得られたということは、そのクラスタ内のセンサーの依存関係が判明したということになり、クラスタ自身を解釈する手助けになります。
今回は、このTICCを使うことも考えましたが、実験のしやすさの観点から、Hidden Markov model(HMM)によるSTS clusteringを行うことにします。具体的には、HMMから生成した人工データに対する復元のデモンストレーションを行います
HMMによるSTS clustering
時系列的なデータとしての性質を強調するため、HMMの遷移行列を工夫しています。具体的には、HMMが少し有利になるように、一部の遷移が頻出しやすいように遷移確率に偏りを持たせました。
import numpy as np
from hmmlearn import hmm
from sklearn.mixture import GaussianMixture as GMM
from sklearn.metrics import adjusted_mutual_info_score
import statistics
import matplotlib.pyplot as plt
import seaborn as sns
np.random.seed(2020)
人工データの生成
num_clusters = 5
model = hmm.GaussianHMM(n_components=num_clusters, covariance_type="full")
model.startprob_ = np.array([0.2, 0.3, 0.1,0.2,0.2])
model.transmat_ = np.array([
[0.6, 0.01, 0.01,0.35,0.03], # 0->0, 0->3
[0.01, 0.5, 0.45, 0.01,0.03], # 1->1, 1->2
[0.45, 0.03, 0.5, 0.01,0.01], # 2->2, 2->0
[0.03, 0.02, 0.2, 0.5,0.25], # 3->3, 3->2, 3->4
[0.01, 0.25, 0.03,0.01,0.7] # 4->4, 4->1
])
model.means_ = np.array([[0.0, 0.0, 0.0], [1.0, 2.0,3.0], [5.0,-10.0,0.0],[-5.0, 10.0,5.0], [10,5.0,0.0]])
model.covars_ = np.tile(np.identity(3), (5, 1, 1))
X, Z = model.sample(200)
train_X = X[:100]
test_X = X[100:]
train_Z = Z[:100]
test_Z = Z[100:]
print(train_Z)
# array([4, 1, 2, 0, 0, 0, 0, 0, 3, 4, 4, 4, 4, 4, 4, 1, 1, 2, 4, 4, 4, 4, 2, 2, 2, 2, 2, 0, 3, 2, 2, 0, 0, 3, 3, 3, 3, 4, 1, 1, 1, 2, 2, 1, 1, 2, 2, 0, 3, 2, 2, 2, 0, 0, 0, 0, 3, 3, 3, 3, 0, 0, 0, 0, 1, 2, 2, 0, 4, 4, 1, 1, 1, 1, 2, 0, 0, 3, 3, 3, 4, 4, 4, 1, 1, 2, 2, 0, 3, 3, 3, 4, 4, 4, 4, 4, 4, 4, 4, 4])
クラスタ数の決定
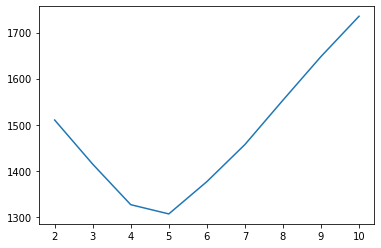
今回もトイデータのため、クラスタ数はわかっていますが、実際のケースを意識して、BICを見てみたいと思います。
bic_clusters = []
# cluster数を2〜10でBICを確認する
for n_components in range(2,11):
bics = []
# 初期値を変えて10回試行する
for i in range(10):
hmm_model = hmm.GaussianHMM(n_components=n_components, covariance_type="full", n_iter=100)
hmm_model.fit(train_X)
score = hmm_model.score(train_X)
n_features = hmm_model.n_features
mean = hmm_model.means_
covs = hmm_model.covars_
# 共分散を対角行列にしているので、非ゼロ成分のみを見ています。
num_parameters = len(np.where(mean*mean >= 0.1)[0]) + len(np.where(covs*covs >= 0.01)[0]) + n_components*(n_components-1) + (n_components-1)
cur_bic =np.log(len(train_X)) * num_parameters - 2 * score
bics.append(cur_bic)
bic_clusters.append(statistics.mean(bics))
plt.plot(list(range(2,11)), bic_clusters)
図のように、こちらが設定したクラスタ数:5でBICが最小となることが確認できました。
AMIと対数尤度による定量評価
こちらも、行列の場合と正解ラベルが存在するため、AMIを算出できます。また、通常の場合を想定して、データとの類似度としてテストセットに対する対数尤度も計算します。ベースライン手法として、時系列を考慮していないGaussian mixture model (GMM)を設定しました。
まずは、AMIを確認します。
ami_hmm = []
ami_gmm = []
for i in range(10):
hmm_model = hmm.GaussianHMM(n_components=5, covariance_type="full", n_iter=100)
hmm_model.fit(train_X)
Z2 = hmm_model.predict(test_X)
gmm_model = GMM(n_components=5).fit(train_X)
Z3 = gmm_model.predict(test_X)
ami_hmm.append(adjusted_mutual_info_score(test_Z,Z2))
ami_gmm.append(adjusted_mutual_info_score(test_Z,Z3))
print(f"AMI achieved by HMM: {statistics.mean(ami_hmm):.3f}")
print(f"AMI achieved by GMM: {statistics.mean(ami_gmm):.3f}")
# AMI achieved by HMM: 0.972
# AMI achieved by GMM: 0.933
次に、テストセットに対する対数尤度を見てみます。
ll_hmm = []
ll_gmm = []
for i in range(10):
hmm_model = hmm.GaussianHMM(n_components=5, covariance_type="full", n_iter=100)
hmm_model.fit(train_X)
score_HMM = hmm_model.score(test_X)
gmm_model = GMM(n_components=5).fit(train_X)
score_GMM = gmm_model.score(test_X)*len(test_X)
ll_hmm.append(score_HMM)
ll_gmm.append(score_GMM)
print(f"Log likelihood achieved by HMM: {statistics.mean(ll_hmm):.3f}")
print(f"Log likelihood achieved by GMM: {statistics.mean(ll_gmm):.3f}")
# Log likelihood achieved by HMM: -610.684
# Log likelihood achieved by GMM: -625.196
| AMI | Log likelihood | |
|---|---|---|
| HMM | 0.972 | -610.684 |
| GMM | 0.933 | -625.196 |
データ生成時の遷移行列を工夫したこともあり、HMMの方が高いAMIと対数尤度を達成していることがわかります。一方で、今回のトイデータを作成する際に平均値を大きく異なる値にしたことから、今回の人工データのクラスタ間の距離は大きいものと考えられます。そのため、時系列的な振る舞いを考慮していないGMMでも高精度に復元できているものと思われます。
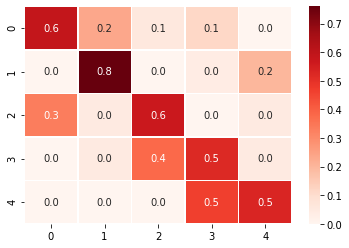
HMMの遷移行列の可視化による定性評価
定性評価として、HMMの遷移行列を確認してみます。クラスタラベルが元の遷移行列と異なるため、容易には比較できませんが、値の傾向を見る限り、良さそうなフィッティングをしていそうなことが確認できました。
このようにデータのみに基づき、クラスタ数やクラスタの遷移傾向までつかむことができました。実際のセンサーデータの場合は、クラスタを表現するガウシアンのパラメータや発生している時刻なども参考に、クラスタ自体を解釈していきます。
sns.heatmap(hmm_model.transmat_, linewidths=.5, cmap="Reds", annot=True, fmt="1.1f")
さいごに
最後までお読みいただきありがとうございます!
今回は、行列、グラフ、時系列データ等、様々なデータに対するクラスタリングについてご紹介しました。
それぞれの手法について定量的な側面と定性的な側面の2方向からアプローチし、データのみから分析可能な特徴についてご紹介しました。
3種類のデータ構造のうち、いずれか1つでも皆さまのビジネス・研究課題のお役に立てれば幸いです!
参考文献
- pLSAとNMFが等価なのか確かめてみた
- Topic modeling on 20 newsgroup data(LSA and LDA)
- LDA (Latent Dirichlet Allocation) を使って英文記事をクラスタリングする(前処理編
- LDA (Latent Dirichlet Allocation) を使って英文記事をクラスタリングする(分類編)
- sklearn.metrics.adjusted_mutual_info_score
- Derivative DTW ~時系列パターンの類似度計算の手法~
- グラフ分割と固有値問題
- 3部モジュラリティの改善とその最適化手法
- SCAN: A Structural Clustering Algorithm for Networks
- networkx.algorithms.cuts.conductance
- networkx.algorithms.community.quality.modularity
- Is there a best quality metric for graph clusters?
- Toeplitz Inverse Covariance-Based Clustering of Multivariate Time Series Data
- 潜在的グラフ構造からの異常検知