深層距離学習(Deep Metric Learning)各手法の定量評価 (MNIST/CIFAR10・異常検知)

はじめに

Metric learningは顔認証システム、異常検知など幅広く利用できる重要な基礎技術ですが、学習方法が特殊だったり、発展している多くの手法のうちどれを選べばよいかなど、ハードルはそれほど低くありません。しかし、特に顔認識システムで発達したArcFaceなどの手法は、「モダンな深層距離学習 (deep metric learning) 手法: SphereFace, CosFace, ArcFace」でも強調されているように_普通のCNN分類器で学習できる_ ため工学的価値が高く、魅力的です。

まず前回の記事「分類器で学習できるMetric learningを簡潔なコードで試す」で距離が期待通り学習されるのかを可視化しましたが、十分評価できませんでした。

そこで異常検知の問題設定をできるだけ網羅的に交差検証するなどして、定量評価しました。コードは下記のgithubリポジトリをご利用下さい。

• コードやノートブックを用意したgithubリポジトリ https://github.com//daisukelab/metric_learning

主な更新履歴:

• 2020/1/27 記事内容の表現、言葉の定義の曖昧さ、不十分な内容を修正しました。

1. 問題設定

• 定番のデータセットMNIST、CIFAR10を使用。(例えば最近の論文[7]でもこれらで評価)
• 一部のクラスを学習させて正常データ(Normal)として扱い、学習していない残りのクラスを異常(Anomaly)として判別する、CNNの異常検知に関する実験で一般に試される問題を設定。
• 判別しやすいクラス(他のどれとも似ていない)、難しいクラス(他に似た形のクラスがある)があるため、クラス数分の組み合わせを試すことで、できるだけ統計的な答えを求める(※全網羅にはなっていません)。
• 正常・異常に割り当てるクラスの数によっても性能が変わることが考えられるため、3種類のクラス数割当別に評価。
• 距離を測る方法としてcosine類似度の他、ユークリッド距離の場合も評価。
• モデルはResNet18、出力されるembeddingsは512次元。fast.aiを使って実装。

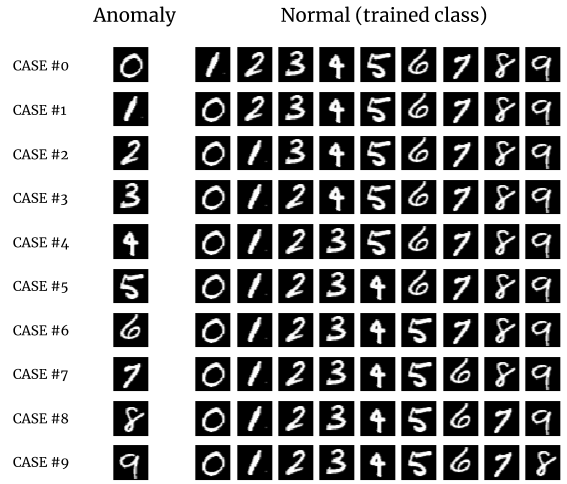
　　図: 異常1:正常に9クラスを割り当てる場合の10テストケースの組み合わせ (MNIST)

　　図: 異常5:正常に5クラスを割り当てる場合の10テストケースの組み合わせ (CIFAR10)

1.1 評価対象

1. Conventional = 距離学習を利用しない通常のCNNの場合
2. L2-constrained Softmax Loss [1]
3. Arcface [2]
4. CosFace [3]
5. SphereFace [4]
6. CenterLoss [5]

1.2 評価条件の組み合わせ

すべての手法は、下記条件の組み合わせで評価しました。

No.	Dataset	異常クラス数	正常クラス数	距離関数(相当)
1	CIFAR10	1	9	Cosine similarity
2	CIFAR10	1	9	Euclidean distance
3	CIFAR10	5	5	Cosine similarity
4	CIFAR10	8	2	Cosine similarity
5	CIFAR10	8	2	Euclidean distance
6	MNIST	7	3	Cosine similarity
7	MNIST	5	5	Cosine similarity
8	MNIST	5	5	Euclidean distance

各組み合わせにつき、上図で表した10テストケースをそれぞれ実施して統計をとっています。

まとめ:

• 10テストケースでは、正常・以上に割り当てる具体的なクラスを入れ替える。
• 8つのセットで評価の条件を組み合わせ、各条件で10テストケースすべてを実施した上で統計をとった結果を出している。

1.3 評価方法

ひとつの組み合わせは10テストケース実施それぞれで、①AUC、②各クラスサンプルの平均距離を得た。

ひとつのテストケースの評価手順

1. 通常のCNN分類器(ResNet18)に、手法を組み込む。(Conventionalのときは何もせずそのまま使う)
2. 学習は、「正常」に割り当てたクラスだけで構成する学習データセットを使い、転移学習によって行う。学習データは、各データセットで元々trainセットに入っているサンプルのみ利用する。
3. 評価データの距離を得る。
   1. 正常・異常を問わずすべてのクラスから評価データを用意、このとき各データセットで元々validセットにあるサンプルを使う。
   2. すべての評価データを、学習したモデルに与えて出力のembeddingsを得る。
   3. 距離を計算する。学習データのembeddings x 評価データのembeddings。※具体的な距離計算はcosine類似度かユークリッド距離。
   4. 評価サンプルjごと、すべての学習サンプルへの距離のうち一番短い値をその評価サンプルの距離$distance_j$とする。 $distance_{j} = min([距離計算(emb_{i}, emb_j) \text{ for i in 学習サンプル}])$
4. 平均距離を計算する。評価データ全てのサンプルの距離を一旦クラス別に平均、このテストケースでのクラスごとの平均距離として得る。その後平均距離のグラフで「Normal」で表示されているものは 正常 に割り当てた各クラスの値のボックスプロットで、「Anomaly」と書いているものは 異常 に割り当てた各クラスの値をプロットしている。
5. AUCの計算は、評価サンプル別に得られた距離をもとにしている。評価サンプルはそれぞれ距離distance_j(正常からの距離)が計算されているため、サンプルが正常・異常どちらのクラスかを正解ラベルとして計算している。※もちろん学習したクラスのとき正常(Normal)ラベル、学習していないクラスには異常(Anomaly)ラベルを割り振る。

2. 評価結果

2.1 結果の見方について

「CIFAR10・異常クラス数5・cosine類似度」の結果をサンプルに、見方について解説します。クラスの割当てはこのようになります。どちらも5クラスずつですが、テストケース10通りで割り当てるクラスをずらしていっています。

結果には__AUC__、__平均距離__がありますが、すべての手法を横並びに表示して、比較できるようになっています。

　　　AUC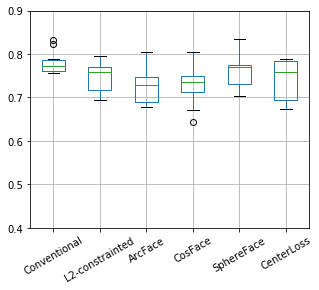　
　　　グラフ: それぞれの手法について、10テストケース分のAUCをボックスプロット。

　平均距離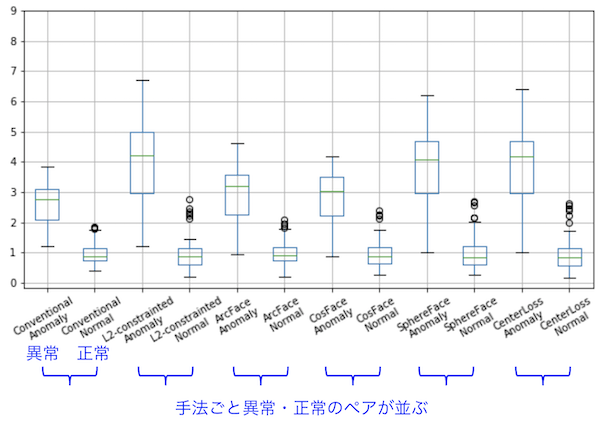　
　　　グラフ: 異常と設定したクラス・正常クラスの平均距離を10テストケース分ボックスプロット。
　　　　　　　※ 距離は正常サンプルの平均距離を使ってノーマライズ。

距離のノーマライズにいて

それぞれの手法の結果得られる距離は、スケールがまちまちなので比較が困難です。またこの距離を使ったシステムを設計する際を考えても距離がまちまちでは使いにくいため、手法によらず一貫した大きさの数値が望まれます。

そこで、正常サンプルの平均距離が「1」になるよう正規化して、この基準で異常サンプルも正規化することで

　　「正常ならば平均距離1なのに対して、異常な場合平均4.5で距離が得られる」

といった理解で取り扱うことが出来ます。この記事で以後表示する距離はすべて正規化済みです。

参考) 異常検知出来なかったサンプル例

定量評価とは別ですが、結果をイメージしやすくするため、どういう画像の距離が近いかを見てみたいと思います。
「CIFAR10・異常クラス数5・cosine類似度」を下記のクラス分けで学習したモデルの例です。

　　異常クラス = [bird, car, cat, deer, dog]
　　正常クラス = [frog, horse, plane, ship, truck]

また間違え方から、モデルの振る舞いを少しだけ観察します。

・Conventional

異常サンプルを正常と間違ったうち、最も短い距離になった5サンプルを表示しています。上が間違った異常サンプル、下はこのサンプルに最も距離が近い正常サンプルです。…とはいえ、明らかにおかしなものはないようです。

・L2-constrained Softmax Loss

どうでしょうか、Conventionalに比べると、例えば右端の猫の顔に一番近いのがカエルで、納得し難い間違え方をしているように見えます。

・Arcface

・CosFace

左から二番目のカエルの結果を見るとモデルの推論は正しいようです。この例は、正解ラベルのミスが見つかったということでしょう。

・SphereFace

間違え方はArcFace/CosFaceに劣るように見えます。

・CenterLoss

比較的良い間違え方に見えます。

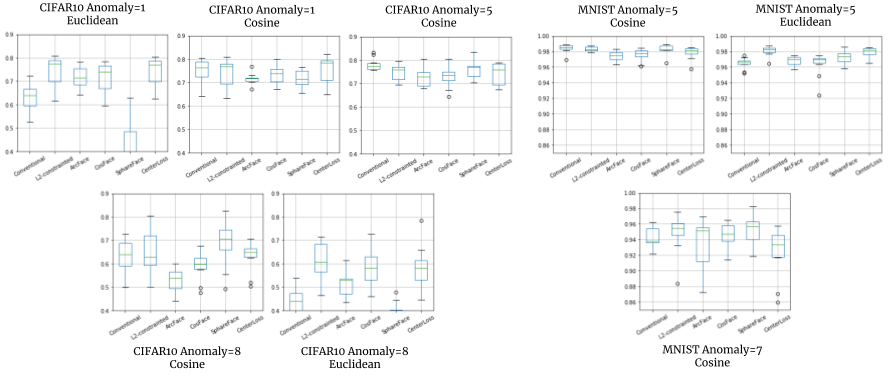
2.2 全ての評価結果と考察

前置きが長くなりましたが、いよいよすべての評価結果を見ていきます。

　　グラフ: 全ての評価で得られたAUC。

全体の結果として、一貫して良いものはなく、どれがいい?と簡単に言える結果ではありませんでした。
強いて言えばL2-constrained Softmaxが安定しているかもしれませんが、単なるCNNが一番性能が良いこともあります。
この結果とノーマライズした平均距離を併せて考察していきます。

応用したい問題によって、有効な手法が変わってくる様子

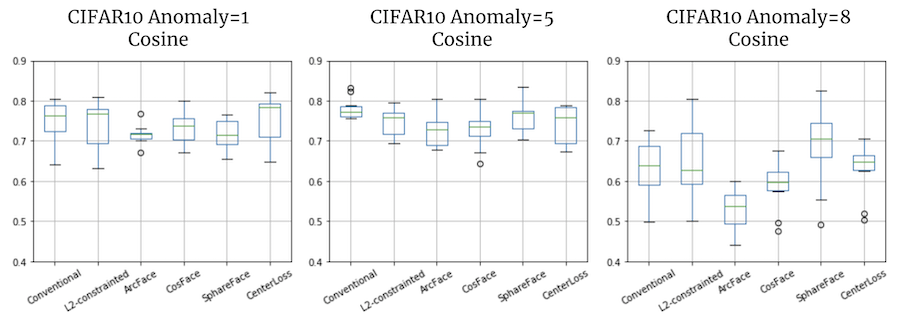
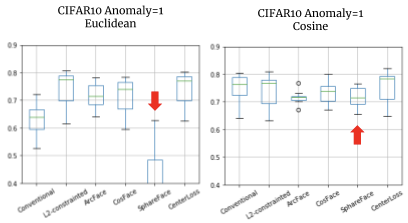
右から、異常クラスの量を1つ(正常9つ)、5つ(正常5つ)、8つ(正常2つ)とバランスを変えた場合のAUCの結果です。
左の２つはほとんど同じ結果、おそらくここまでは問題が簡単すぎるということかもしれません。

一番右、大半を異常クラスにした場合、SphereFaceは他の手法に比べて平均AUCが5%以上良い結果を示しました。
(n=2回実施して再現)
正常に比べて異常のバリエーションが多い場合ですので、そういうケースに有効なのかもしれません。
あるいは他のハイパーパラメーターと併せて、たまたま性能が出ているのかもしれません。

データ/パラメーターが確定する最後の瞬間まで、手法を比較評価できるようにしたほうが当然有利だし、むしろ必要だと言えるのかもしれません。

AUCと併せて異常サンプルの距離も検討材料に

この結果をAUCだけ見ると、Conventionalな普通のCNNだけを使えば一番性能が出そうです。
　　　AUC　
ところが平均距離を見ると、(正常1に対して) Conventionalは異常サンプルの距離は平均2.8程度、他の手法では距離4を超えているものもあり、そちらの方がマージンを取れそうです。
　平均距離　

どのような異常を想定するか、それは(疑似でも)データが用意できているのか、そういった状況でどの程度マージンを取るかなど、検討の余地がありそうです。

AUCが良すぎる・平均距離の差が大きすぎる⇒評価出来ていないのでは

MNISTでは、異常とするクラスを多くしてもAUCは0.95程度まで得られてしまいます。
　　　AUC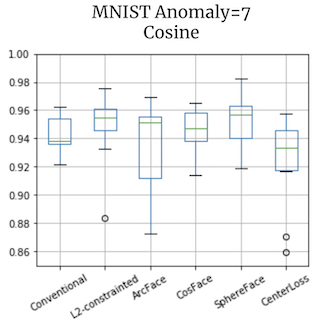　
距離も、正常1に対して異常13〜20までの差を出せています。
　平均距離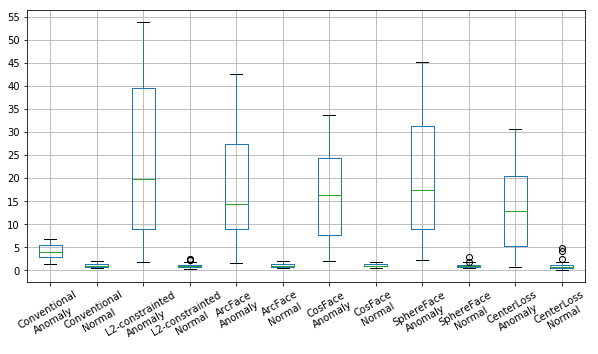　

この場合そもそもデータが簡単すぎて、応用したい問題に対する評価対象になっているのか、考え直すきっかけを示しているかもしれません。またこの実験ではそもそもMNISTを扱うにはモデルの表現力が高すぎたとも考えられます。その点でも評価に疑問符がついたのかもしれません。

「正常」のバリエーションを増やすと「異常」の距離スケールが小さくなる

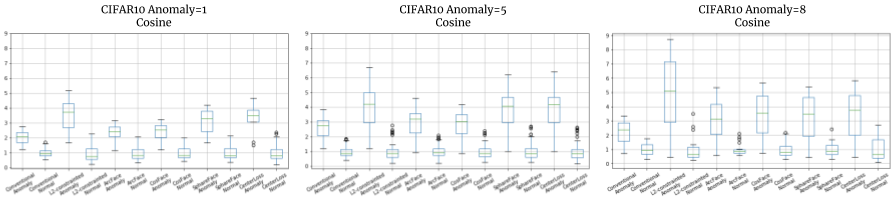
右から、異常クラスの量を1つ(正常9つ)、5つ(正常5つ)、8つ(正常2つ)とバランスを変えた場合の平均距離の結果です。
縦軸は合わせてありますので、正常クラスの数が減るほど異常なときの距離が長く測られているようです。

当然考えられることですが、何でも正常とみなすようにデータを追加してしまうと、異常なクラスに似たものまで混入したりして、性能が下がる要因になる例として理解できるかもしれません。またデータが多ければ良いわけではなく、何を正常とするか整理されていることが大事で、そのための条件を整えましょう、ということを示しているかもしれません。
(機械学習プロジェクトの普遍的課題でしょうか…)

cosine類似度 vs. ユークリッド距離

確認まで実施した意味ではありますが、特にユークリッド距離を使うことで良い結果になったこともなく、やはりcosine類似度を使うほうが良い結果でした。

逆にユークリッド距離を使うことで問題がいくつか見つかりました。

コラム: 今回の実験では角度で評価すべき?

2020/1/27 更新: 内容を大きく書き換えました。

どう評価するのが一番望ましいかを考え始めた当初「Embeddingsの学習インセンティブはベクトルの内積ではないか…」と考えましたが、そういうことではなかったようで、今回比較した手法自体に概ねその答えがありました。

(ArcFace[2]から引用、Cross Entropy Lossの計算式)

根本的なこの式のうち、xがモデルの出力したembeddingsでありサンプルを表すベクトルと見做せて、重みWはクラスを表す同じ次元のベクトル、と解釈するのは間違いないはずです。※簡単のためバイアスbはこの検討から外します。

• ArcFace/CosFaceなどは、元々Wとxを単位円(球体?)上に投射、それらのなす角のcosθを計算して(cosine類似度)、その角度が小さくなるようにlossが計算されます。言い換えると、サンプルとのcosine類似度が小さくなるようにクラスの重みが更新されていくので、cosine類似度の大小が指標として学習されます。このcosine類似度がリニアかどうかはわからないものの、サンプル間でも(正常からの距離として)相対比較して使えるように学習が設計されていました。
• 通常のCNNでは、W^T xが大きくなるように学習が進むため、このxをサンプル間でどう比較すればよいのかは、学習設計では特に考慮されていない、ということになりそうです。ただ、cosine類似度でもユークリッド距離でも、距離として概ね働くようではありますが。

つまり、設計や品質の観点からすると、

• ArcFace等cosine類似度が小さくなるよう学習が設計された手法を使ってモデルを学習すること
• cosine類似度でサンプル間の距離を比較すること

が設計通りの使い方ということになりそうです。その他の方法でもある程度の結果が出ているものの、手法がそのように設計されているわけではないので、品質が より 保証できないことになります。もちろんArcFace等を使ったとしても結果は保証できないでしょう。「原理的にどうなる」ように設計するか、この点が説明性の観点からも重要だと考えられます。

問題点: ユークリッド距離⇒異常の距離スケールが小さくなる

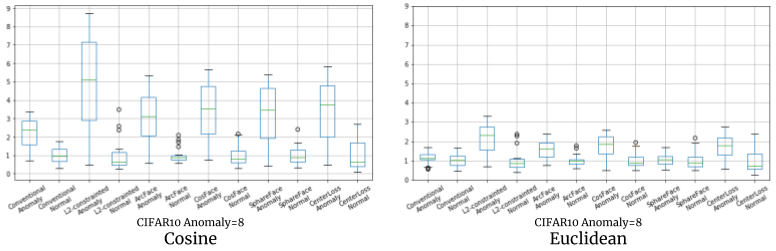
この結果のように、cosine類似度で異常の距離は正常の数倍になるのに対して、ユークリッド距離ではほとんど正常と同じになる場合があり、検知の運用が難しくなりました。

問題点: 特にSphereFaceの性能低下が著しい

SphereFaceとConventionalは、cosine類似度でないと性能が出ないことがわかりました。
SphereFaceのAUCは0.5を下回っており、「ランダムに答えを出すモデルのAUCは0.5」よりも悪い結果となっています。

2.3 Embeddingsを可視化

定量評価ではありませんが、前回の記事では納得の行く結果の出なかったembeddingsの可視化を再び試みました。

すべてのクラスを学習させたときの、評価セットのembeddingsを可視化したものです。
※つまり異常検知ではなく、単純なクラス分類問題の学習結果です。
結果として、MNISTではうまく行かなかった可視化は、CIFAR10を使うことである程度うまく行っているように見えます。

・Conventional

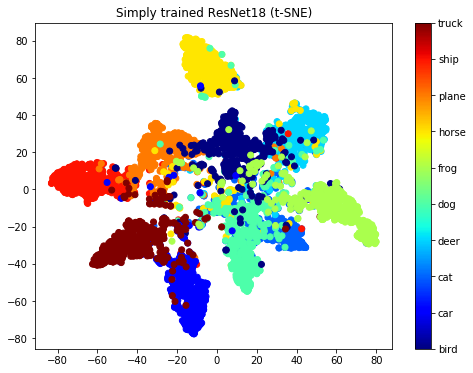
　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

・L2-constrained Softmax Loss

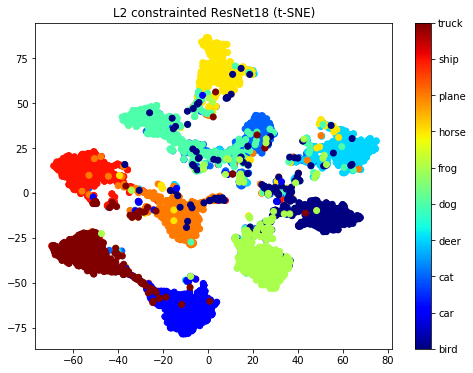
　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

・Arcface

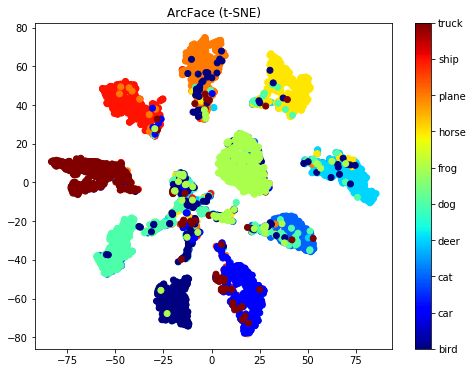
　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

クラスのクラスタがはっきり分かれています。ここまでクラスタ間の距離でマージンが取れていると、その後のdiscriminativeな判断用途で有利なように見えます。
　※ 11個の島になっていて、一つだけ特にいろんなクラスが混じっているものがあります。このクラスタのサンプルは特に難しかったり、ラベルのミスがあるものとして取り扱えそうです。

・CosFace

　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

・SphereFace

　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

・CenterLoss

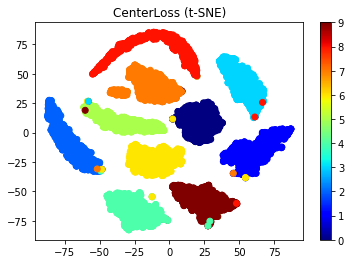
　　　　図: Embeddingsのt-SNE二次元可視化　左:CIFAR10、右:MNIST

Annex: 追加検証

コメントを頂いた2点、追加で検証を行いました。

• A.1 評価サンプルの距離を「全ての学習データポイントからの最小距離」ではなく、「数個の正常データとの距離の平均値」にした場合はどうか
• A.2 少ないサンプル数のときはどうか、普通のCNNに比べて距離学習の頑強性が有利に働くのではないか

A.1 評価サンプルの距離を最小K個の平均距離としたとき

評価データの距離は、全ての学習データとの最小距離をとっていました。

for x_j in すべての評価データ:
  score_j = min([distance(x_j, x_i) for x_i in 全ての学習データ])

ところが特にCIFAR10のデータセットにはノイズが多く見られます。クラスラベルからややそれたコンテンツ、それ以前に間違ったラベルが付けられたサンプルもあります。これらのノイズがあるデータに対して、たまたま最小距離になっているのではと思われる様子がその後の実験で見られました。

本来ノイズは発生源を抑えるべきですが、大量の画像データの場合困難です。そこで出力された距離が短いものからK個の平均を取ることで、ノイズの影響を抑えられないかという検証になります。

def mean_k_min(distances, K=5):
  return mean(sort(distances)[:k])

for x_j in すべての評価データ:
  score_j = mean_k_min([distance(x_j, x_i) for x_i in 全ての学習データ])

※実際のコードはまとめてベクトル演算。

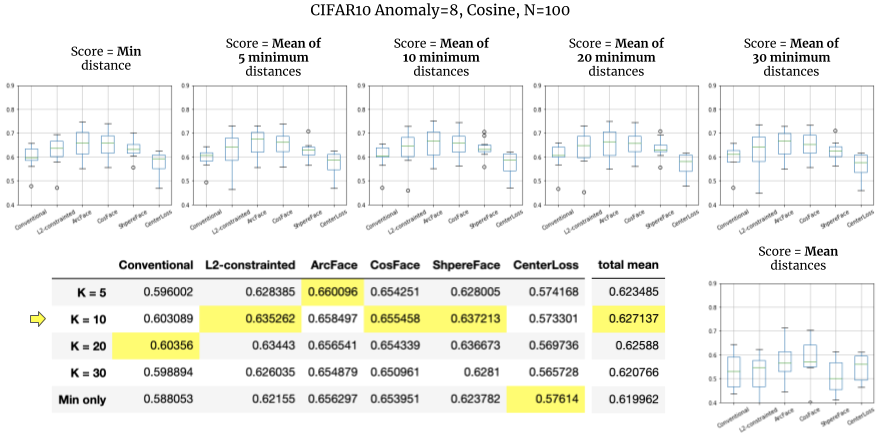
クラスサンプル数 N=100、K=5, 10, 20, 30 の他、全ての学習データとの距離平均としたときも見てみました。
2クラスを学習、評価サンプルにはそれ以外8クラスが割り当てられました。

検証結果

効果はややありました。

• 今回の実験設定では、K=10のときに最大の効果となりました。学習データ数 N=100 * 10クラス = 1,000枚に対して K=10 のとき 10 / 1,000 = 1% のサンプルの平均を取ることになります。
• 下の表はKに対するそれぞれの手法の平均AUCですが、Kに対してすべての手法を平均すると 0.627137 - 0.619962 = 約0.7% 性能が上がる計算結果です。※ Kaggleなら重要な一歩になりかねません。

また、単純に平均をとった場合(右下のグラフ)はとてもスコアが下がっています(約10%の低下)。やはり最小値に近い群で__ノイズを緩和して適正な距離を算出する__ 意味合いが強かったのではと思われます。

間違え方に着目すると、ノイズを回避している様子が伺えます。上の段は「スコア = 単純な最小距離」、おそらく最小が出やすいのであろう学習サンプルに間違いが集中しているようです。下は「スコア = 最小30距離の平均」ですが、平均を取ると回避されている様子を示している可能性があります。

　　評価データのクラス Anomaly = ['bird', 'car', 'cat', 'deer', 'dog', 'frog', 'horse', 'plane']
　　学習データのクラス Normal = ['ship', 'truck']

A.2 少ないサンプルの場合の比較

CIFAR10では1クラス5,000枚のデータが用意されています。この数を1クラス当たり100枚程度、実際に応用するときに現実的に有り得そうな量にした場合について比較してみました。

クラスサンプル数は、 N=50, 100, 200, 300, 400, 500 で比較しました。
また、Conventional(通常のCNN)の場合は少ないサンプルでは学習がうまく進まず比較に不利な条件となりますので、「小さなデータセットで良い分類器を学習させるとき」で確認したようにmixupを適用します。
※ L2-constrainedにも適用、Arc/Cos/SphereFaceには(実装の都合上)mixupを適用できませんでした。またCenterLossには適用を忘れました…

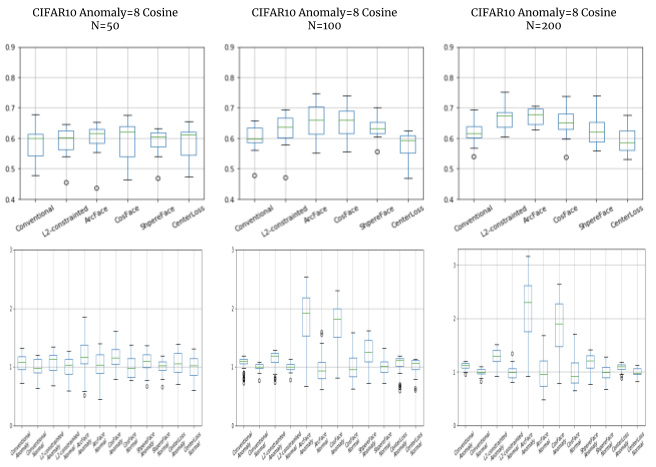
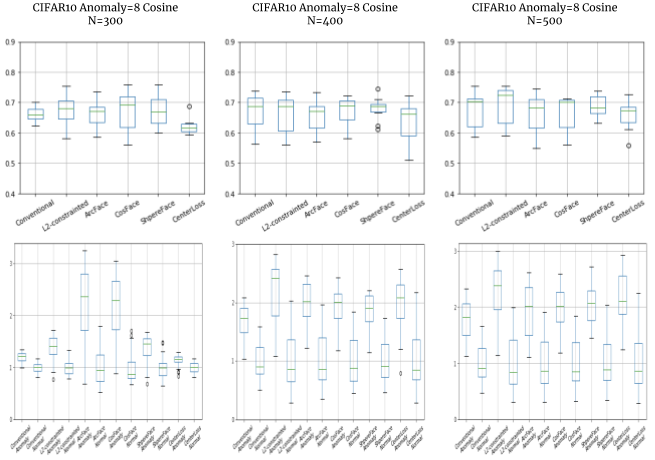
検証結果

こちらも想定通り、少ない枚数(N=100, 200)では普通のCNNとDeep Metric learning手法との差が現れました。
Metric learningの中でもArc/CosFaceは、1クラスあたり数枚のデータを学習するFew-shotの問題でも使われて成果を残していますので(@yu4u さんのSlideShare「Humpback whale identification challenge反省会」)、少ない枚数ではやはり有効でしょうか。
これに対して、N=400以上ではどの手法も十分に異常サンプルの距離を大きく測ることが出来ています。
このように、その問題で用意できるサンプル数についても、手法の比較評価を左右することが分かりました。

なおN=50のときは、評価できるレベルの精度で学習出来ていない様子でした。(改善の余地はあります)
また、CenterLossはmixup適用を忘れていますので、結果は無効と考えてもらって結構です…

おわりに

前回の記事で難しかったDeep Metric Learning各種法の評価について、トイ・プロブレムではありますが、異常検知を題材に定量評価について考察しました。

• 距離を正常サンプルの平均距離でノーマライズする方法は、その後の検討で良い指標になりました。実応用を開発するときにも使えるかもしれません。
• 結果の比較方法について、AUCだけでなく距離のマージンについても考える余地がある様子でした。
• 正常とはなにか、異常に何を想定するか、データによって結果にどう現れてくるかについても、少し例が得られたと思います。
• CIFAR10程度のデータであればある程度評価できるが、MNISTだと難しいのかも、しれません。
• Annex追加更新) 学習サンプルの数も比較検討のパラメーターとして重要で、特にサンプル数が少ないときに有利な手法が変わってきそうです。

あまり明るい記事になりませんでしたが、Deep Metric Learningはものすごいポテンシャルがあると思います。
実応用の課題にやや踏み込んでみましたが、実サービスや製品適用へのハードルはそれほど高くないのでは、という所管で締めくくりたいと思います。
今後いろんな応用事例を期待したいですね。

References

[1] R. Ranjan, C. D. Castillo, and R. Chellappa. L2-constrained softmax loss for discriminative face verification. arXiv preprint arXiv:1703.09507, 2017. https://arxiv.org/pdf/1703.09507.pdf
[2] J. Deng, J. Guo, and S. Zafeiriou. Arcface: Additive angular margin loss for deep face recognition. arXiv preprint arXiv:1801.07698, 2018. https://arxiv.org/pdf/1801.07698.pdf
[3] H. Wang, Y. Wang, Z. Zhou, X. Ji, D. Gong, J. Zhou, Z. Li, and W. Liu, CosFace: Large Margin Cosine Loss for Deep Face Recognition, arXiv preprint arXiv:1801.09414, 2018. https://arxiv.org/pdf/1801.09414.pdf
[4] W. Liu, Y. Wen, Z. Yu, M. Li, B. Raj, and L. Song. SphereFace: Deep Hypersphere Embedding for Face Recognition. In CVPR, 2017. https://arxiv.org/pdf/1704.08063.pdf
[5] Y. Wen, K. Zhang, Z. Li, and Y. Qiao, A discriminative feature learning approach for deep face recognition,” in European Conference on Computer Vision. Springer, 2016, pp. 499–515. https://ydwen.github.io/papers/WenECCV16.pdf
[6] Jake Snell Kevin Swersky Richard S. Zemel, Prototypical Networks for Few-shot Learning. arXiv preprint arXiv:1703.05175, 2017. https://arxiv.org/pdf/1703.05175.pdf
[7] Lukas Ruff, el al., Deep One-Class Classification, ICML 2018, http://data.bit.uni-bonn.de/publications/ICML2018.pdf
[8] Hongyi Zhang, Moustapha Cisse, Yann N. Dauphin, David Lopez-Paz, "mixup: Beyond Empirical Risk Minimization," in arXiv:1710.09412, 2017, https://arxiv.org/abs/1710.09412