こんにちは、@daifukusanです。
専門学校でITを教えている傍らで、趣味で機械学習やデータサイエンスを勉強しています。
以前、競走馬ごとの強さを対戦ゲームのレーティングアルゴリズムを使って数値化することを行いました。
ありがたいことに、多くの方に見ていただけて、機械学習の勉強のモチベーションが上がりました。
いいねやストック、コメントを頂いた方、ありがとうございました。
今回も競馬のデータを使って、色々試した結果を紹介します。
競馬分析関連の記事リンク
競走馬の強さの数値化に挑戦する
競走馬のレース適性の数値化に挑戦する ← 本記事
競走馬の強さ、レース適性を数値化したので折角だし使ってみる
1. はじめに
前回、過去のレース結果をもとに、競走馬ごとの強さを数値化しました。
ただ、実際のレースって、この強さの順に勝負が決まることはほぼないんじゃないでしょうか。
理由は、現実のレースの勝敗は様々な要因が複雑に絡み合って決まるはずだからです。
例えば、以下のようなものが勝敗に影響しそうです。
- 競走馬の強さ ← 前回で数値化済み?
- 競走馬とその日のコース状態の相性
- レース展開
3に関しては、レース中の動的なデータがないと分析が難しいため、私の手持ちのデータでは分析できません。
ですが、2に関しては出馬表や過去の成績データなどの静的データから分析できるため、今回はこちらに挑戦しました。
2. 自身の成績からレース適性を数値化する
2.1. 各列の説明
各列の説明は以下になります。
- 距離分類 : 出走するレースの距離を長さで5種類に分類(短距離~長距離)
- 枠 : 枠番が1-3を内枠、4-6を中枠、7-8を外枠と定義
- 方向 : 右 or 左 or 直
- 天気 : 晴、曇、小雨、雨の4種類 (小雪、雪はそれぞれ小雨、雨に統合)
- 馬場 : 芝 or ダート
- 区分 : 平場 or 重賞
- 順位点 : 1着を1、最下位を0として出走頭数で均等に分割した値を割り当て
ここで、距離分類~区分まではレース開始前に決まる情報なので、これをレース条件と呼ぶことにします。
2.2. レース適性を割り出す
上記のレース条件をもとに出走するレースの適性を求めていきます。
考え方を2.2.1~2.2.3で整理しましたが、ソースコードだけ必要な人は2.2.3だけ見て下さい。
2.2.1. それぞれのレース条件の値を列に展開する
はじめに、各レース条件が取りうる値をそれぞれ列に展開します。
例えば、距離分類であれば、['短距離','マイル','中距離','中長距離','長距離']の5つの値を取りうるため、この5つの列を追加します。
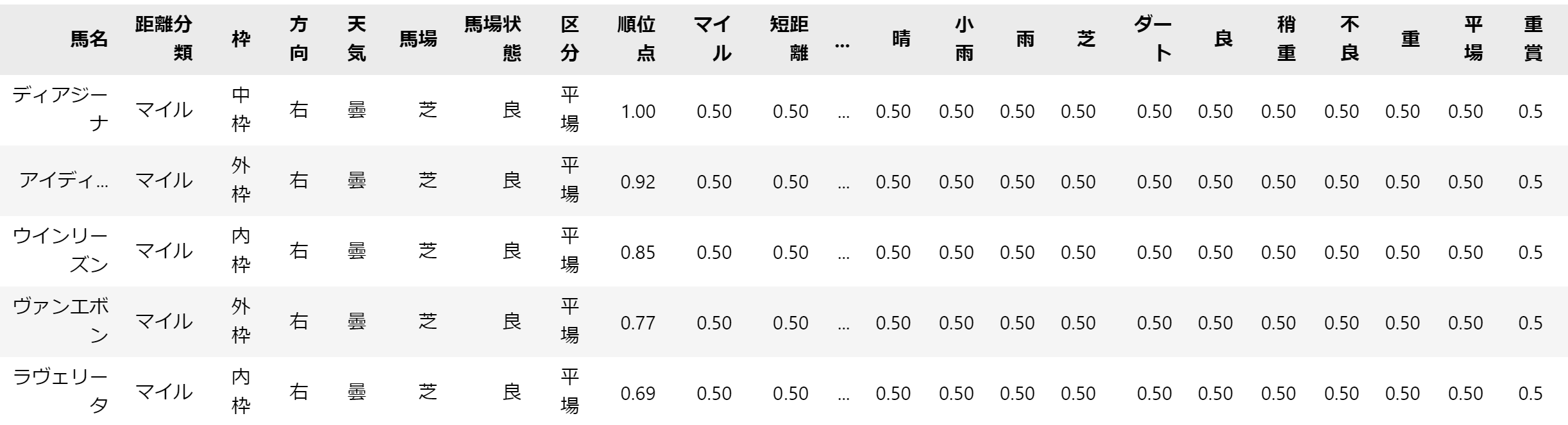
追加後のイメージは以下の通りです。

各列には、「各条件に対するその馬の適性」を格納していきます。
適性は0-1の値をとり、1に近づくほど適性が高くなるように設定するつもりです。
そのため、初期値としてはちょうど中間値である0.5をセットしておきます。
2.2.2. 各レース条件の適性値を更新する
データを時系列順に1件ずつ調べていきながら、レース結果をもとに各適性の値を修正していきます。
このとき、修正する列は、「その馬が出走したレース条件にあう適性列のみ」としています。
以下の例で説明します。
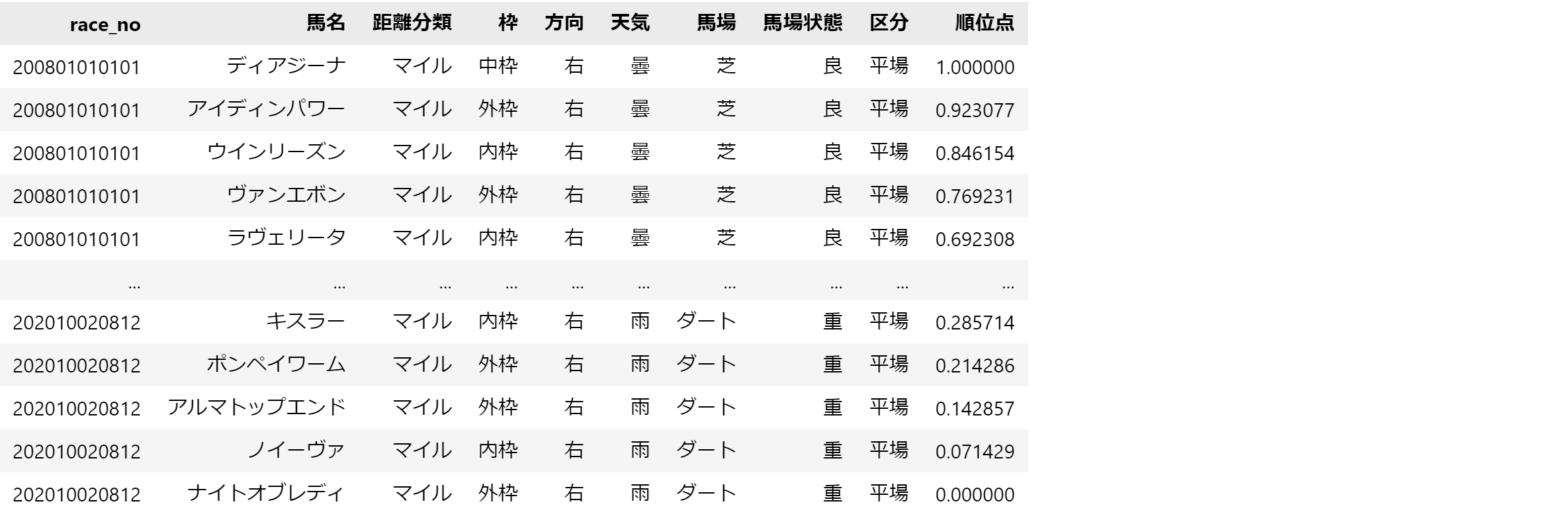
1番上のディアジーナが出走したレース条件は、['マイル','中枠','右','曇','芝','良','平場']となっています。
出走したレース条件以外の適性は、このレースの結果からは判断できないので、更新するのは出走したレース条件と同じ名前の列だけとなります。
次に、具体的などうやって適性値を更新したかを説明します。
適性値を$x$としたとき、$x$の更新式は以下のように定義しました。
$$
x_{更新後} = 学習率 \times 順位点 + (1 - 学習率) \times x_{更新前}
$$
このあたりは、ニューラルネットワークの勾配降下法を参考にして考えました。
学習率は、0-1の値を取るパラメータです。
1に近づくほど直近の成績を重視し、0に近づくほどそれまでの成績を重視します。
私が手元でやったときには、学習率は0.2でいい感じの値が出てくれました。
2.2.3. レース適性値を求める
2.2.2 によって、レース適性値が適切に更新されるようになりました。
最後に、各行の適性値の列を集約して、「競走馬のそのレースにおけるレース適性」を求めます。
これは単純に、「その行の各レース条件の適性の平均値」としました。
このとき、出走したレースの条件に合致する列だけで平均値をとることに注意しましょう。
例えば、['マイル','中枠','右','曇','芝','良','平場']のレースに出た場合、この適性列だけを使って平均を求めます。
また、今回は単純平均を使ってレース適性を求めましたが、距離分類や枠の適性を重視したい場合は加重平均を使うとよいと思います。
ここまでの内容をソースコードにまとめると以下の通りとなります。
lr = 0.2
data_horse = pd.DataFrame()
columns = ['距離分類', '枠', '方向', '天気', '馬場', '馬場状態', '区分']
total_score = [0 for _ in range(data.shape[0])]
for col in columns:
dummy_columns = data[col].unique().tolist()
score_dic = dict()
score_list = [[0.5 for _ in range(len(dummy_columns))] for _ in range(data.shape[0])]
for i, (uma, el, score) in enumerate(data[['馬名', col, '順位点']].values.tolist()):
if uma in score_dic:
score_list[i] = score_dic[uma]
else:
score_dic[uma] = [0.5 for _ in range(len(dummy_columns))]
for j, d in enumerate(dummy_columns):
if el == d:
total_score[i] += score_dic[uma][j]
score_dic[uma][j] = lr * score + (1-lr)*score_dic[uma][j]
break
df_score = pd.DataFrame(score_list, columns=dummy_columns)
df_horse_score = pd.DataFrame(score_dic.values(), columns=dummy_columns, index=score_dic.keys())
data = pd.concat([data, df_score], axis=1)
data_horse = pd.concat([data_horse, df_horse_score], axis=1)
data['レース適性'] = np.array(total_score) / len(columns)
3. 結果の確認
出力結果を確認します。
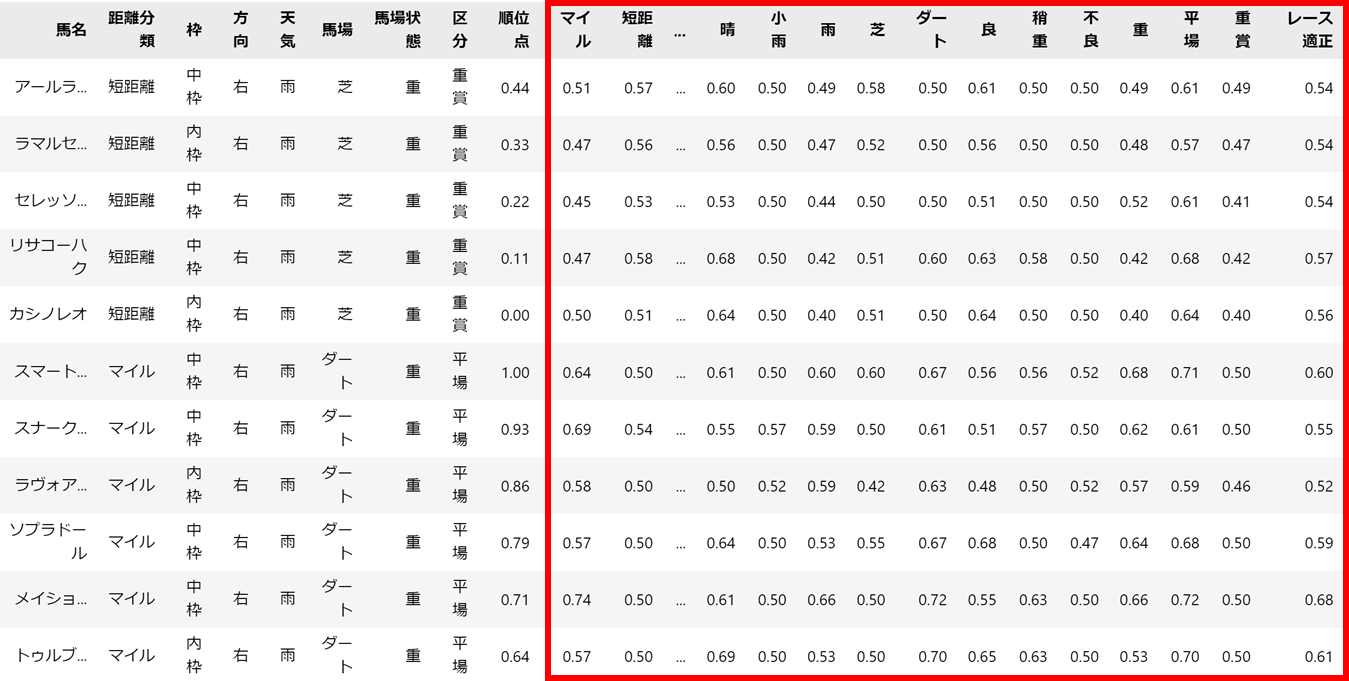
まずは、分析に使用したdataテーブルからになります。
このdataには、元からあった列に、各レース条件の適性列を追加しています。
図の赤枠が追加された適性列です。
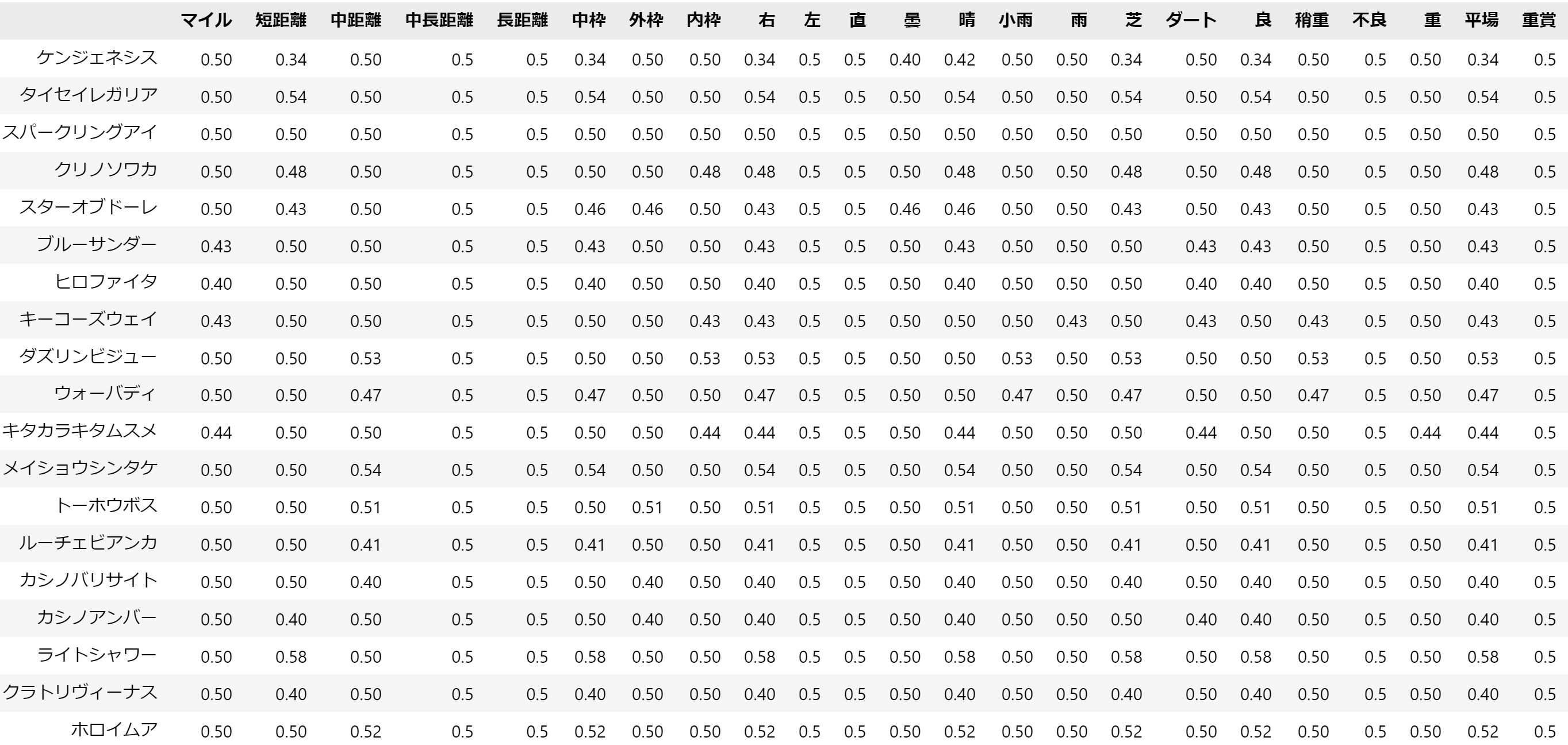
続いて、data_horseテーブルを確認します。
このテーブルは、各出走馬の最後に出走したレース後のレース適性を格納しています。
dataテーブルでは、同じ馬が何度も登場してしまうため、馬同士を比較するなどの用途にはdata_horseテーブルの方が使い勝手が良いと思います。
4. まとめ
今回は、レースごとの条件とそのレースの結果を用いて、競走馬ごとのレース適性を数値化してみました。
本来なら、この結果を使って色々な分析を紹介したかったのですが、ここまでの説明でかなり長くなってしまったので、一旦ここまでとさせてください。
近いうちに、分析した結果もまとめて記事にしようと思っています。