競走馬の強さ、レース適正を数値化したので折角だし使ってみる

こんにちは、@daifukusanです。
専門学校でITを教えている傍らで、趣味で機械学習やデータサイエンスを勉強しています。

以前、競馬データの分析のための数値化に関する記事を2つほど投稿しました。

この強さの指標とレース適正の指標を使って、色々な分析をしてみましたので、その結果を紹介したいと思います。
※上記の2つの記事で導いた指標を使った説明になりますので、先に上の2つの記事を確認していただくことをお勧めします。

競馬分析関連の記事リンク
競走馬の強さの数値化に挑戦する
競走馬のレース適正の数値化に挑戦する
競走馬の強さ、レース適正を数値化したので折角だし使ってみる ← 本記事

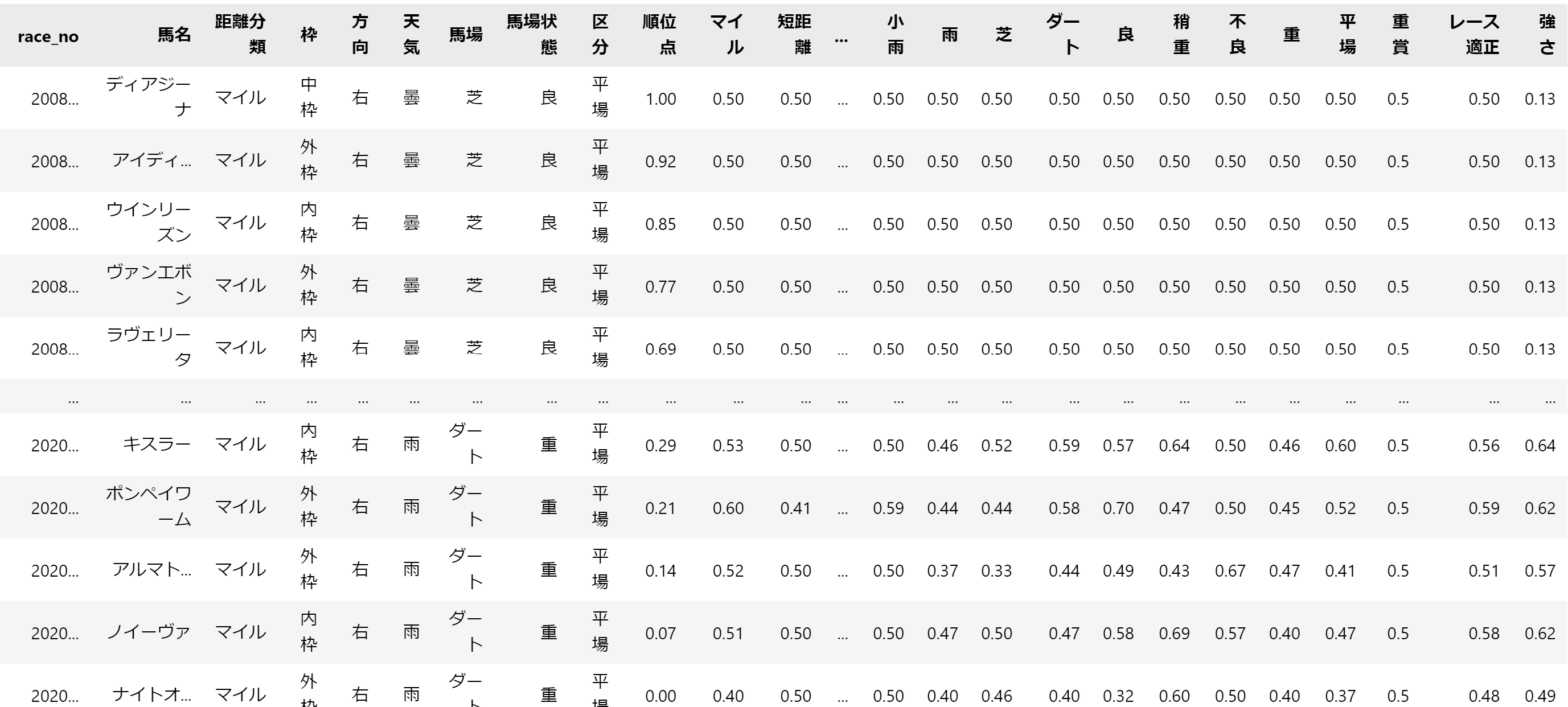
今回対象とするのは、次のようなデータです。

マイル列～レース適正列までが前回もとめたレース適正になります。
一番右の強さ列が前々回に求めた強さの指標です。
強さの指標については、尺度を合わせるために0-1の範囲になるよう正規化しています。

1. レースごとの出走馬のデータを比較する

真っ先に思いつくのが、自分で馬券を購入する際の分析として使うことです。
強い馬、レース適正が高い馬が勝ちやすいと判断できるので、これらの値は馬券購入の手がかりとして使えそうです。

例として、2017年の有馬記念を使ってやってみました。
今回のレースに関連するレース適正のみ抜き出して表示してみます。
表示のためのソースコードは以下の通りです。

pd.set_option('display.max_columns', 25)
pd.options.display.precision=2
pd.options.display.max_colwidth=20

race_no = 201706050811  # ここにrace_noの値をいれる
race = data[data['race_no'] == race_no]
columns = race[['距離分類', '枠', '方向', '天気', '馬場', '馬場状態', '区分']].iloc[0,:].values.tolist()
race = race[['馬名']+columns+['レース適正', '強さ']].set_index('馬名')
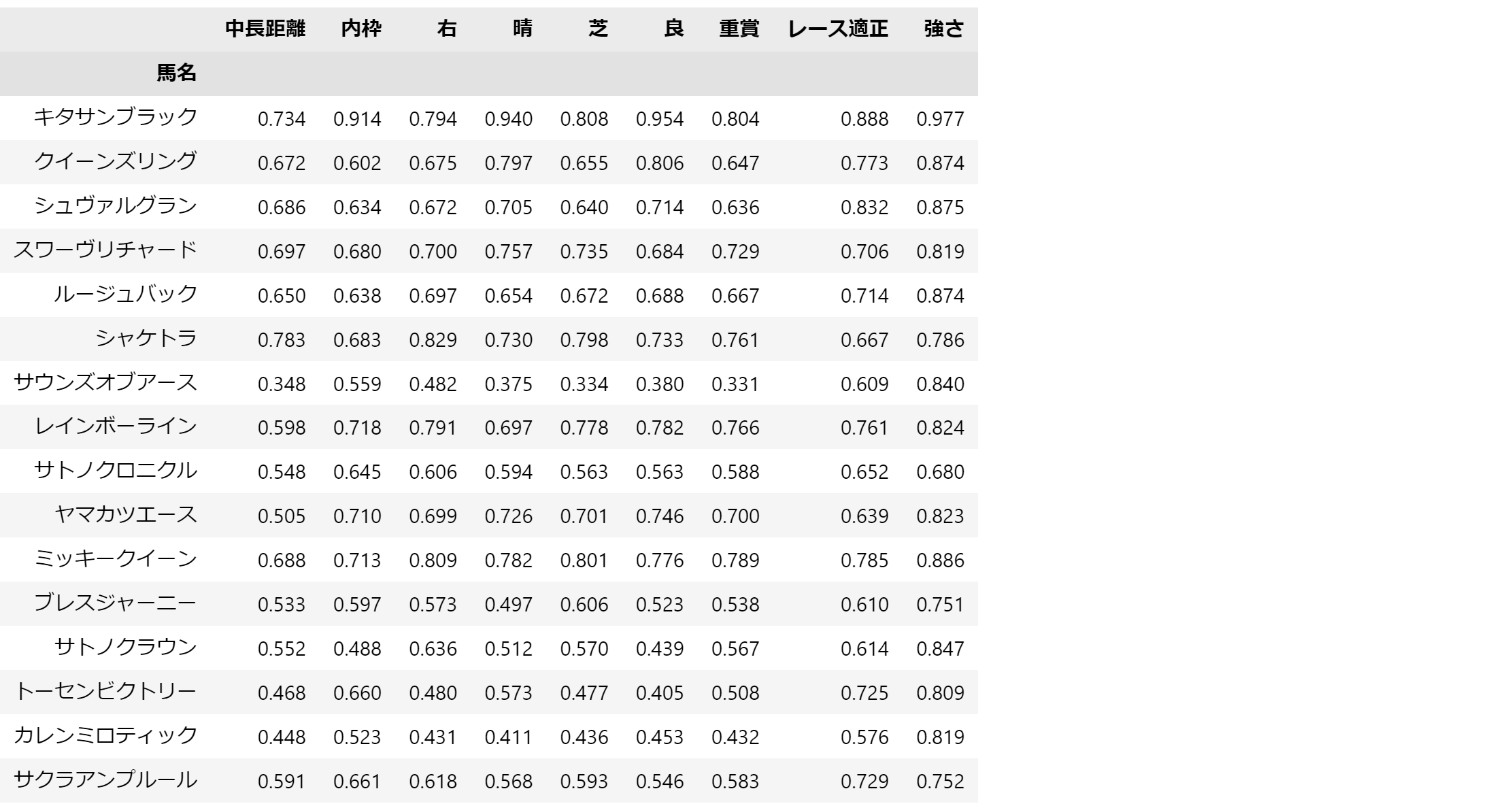
race

結果は以下のようになります。

よく見ると、キタサンブラックがあらゆる指標で高い値を出しています。
ただ、項目が多くて確認しづらいので、こちらをさらにheatmapで確認します。

import seaborn as sns
import matplotlib.pyplot as plt

plt.figure(figsize=(8,6))
sns.heatmap(race, annot=True, fmt='.2f')
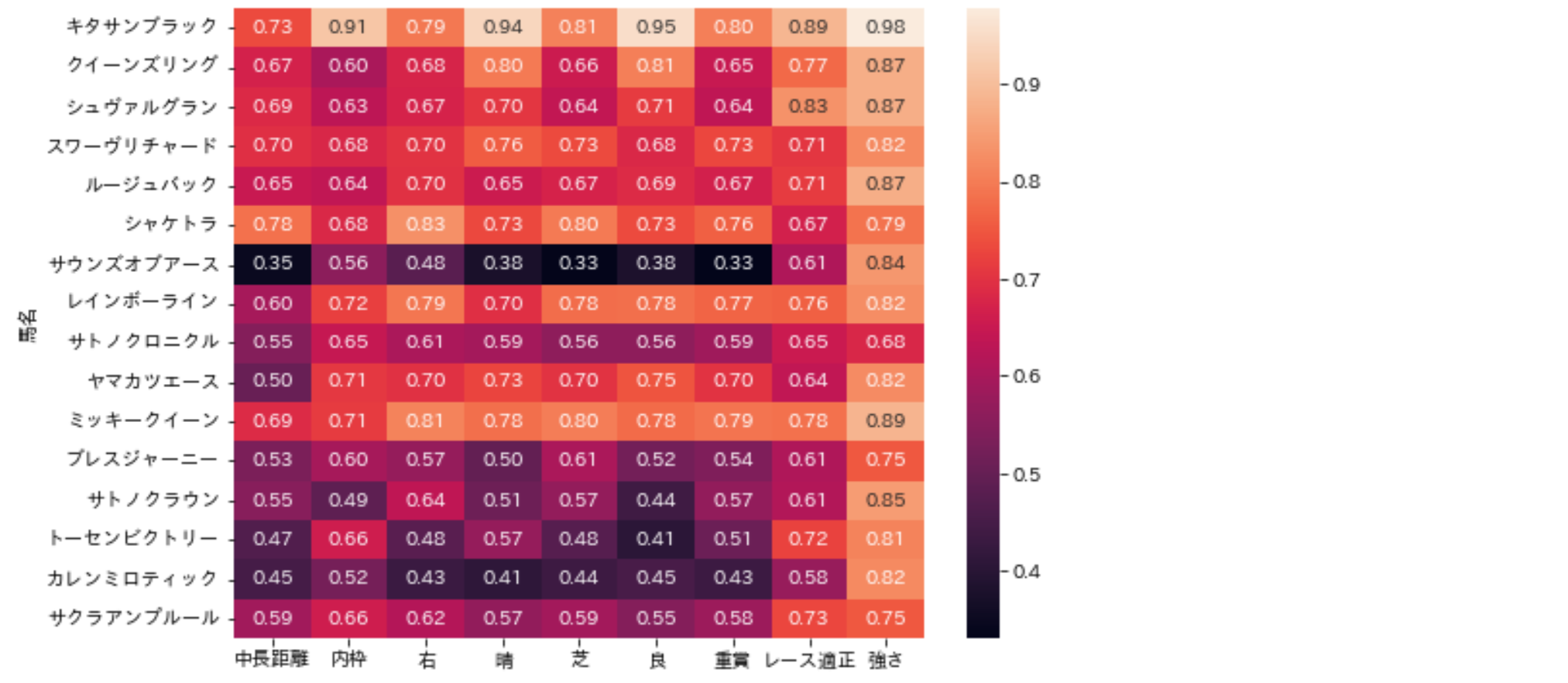
plt.show()

さきほどよりも視覚的に確認しやすくなりました。
このデータは着順でソート済みですが、着順が早いデータほど色が明るくなっています。
これだけ傾向がはっきり表れると、この指標を競馬予測で使ってもよさそうですね。

次にレーダーチャートで各競走馬の適正を表示してみます。

import matplotlib.pyplot as plt
import numpy as np

values = race.values
labels = race.columns
horse_names = race.index

fig, ax = plt.subplots(ncols=4,nrows=4, figsize=(20,20), facecolor="w", subplot_kw=dict(polar=True))
ax = ax.flatten()
for i, name in enumerate(horse_names):
    radar_values = np.concatenate([values[i], [values[i][0]]])
    angles = np.linspace(0, 2 * np.pi, len(labels) + 1, endpoint=True)
    ax[i].plot(angles, radar_values)
    ax[i].fill(angles, radar_values, alpha=0.2)
    ax[i].set_thetagrids(angles[:-1] * 180 / np.pi, labels)
    ax[i].set_ylim([0.0, 1.0])
    ax[i].set_title(name, pad=20)
plt.show()

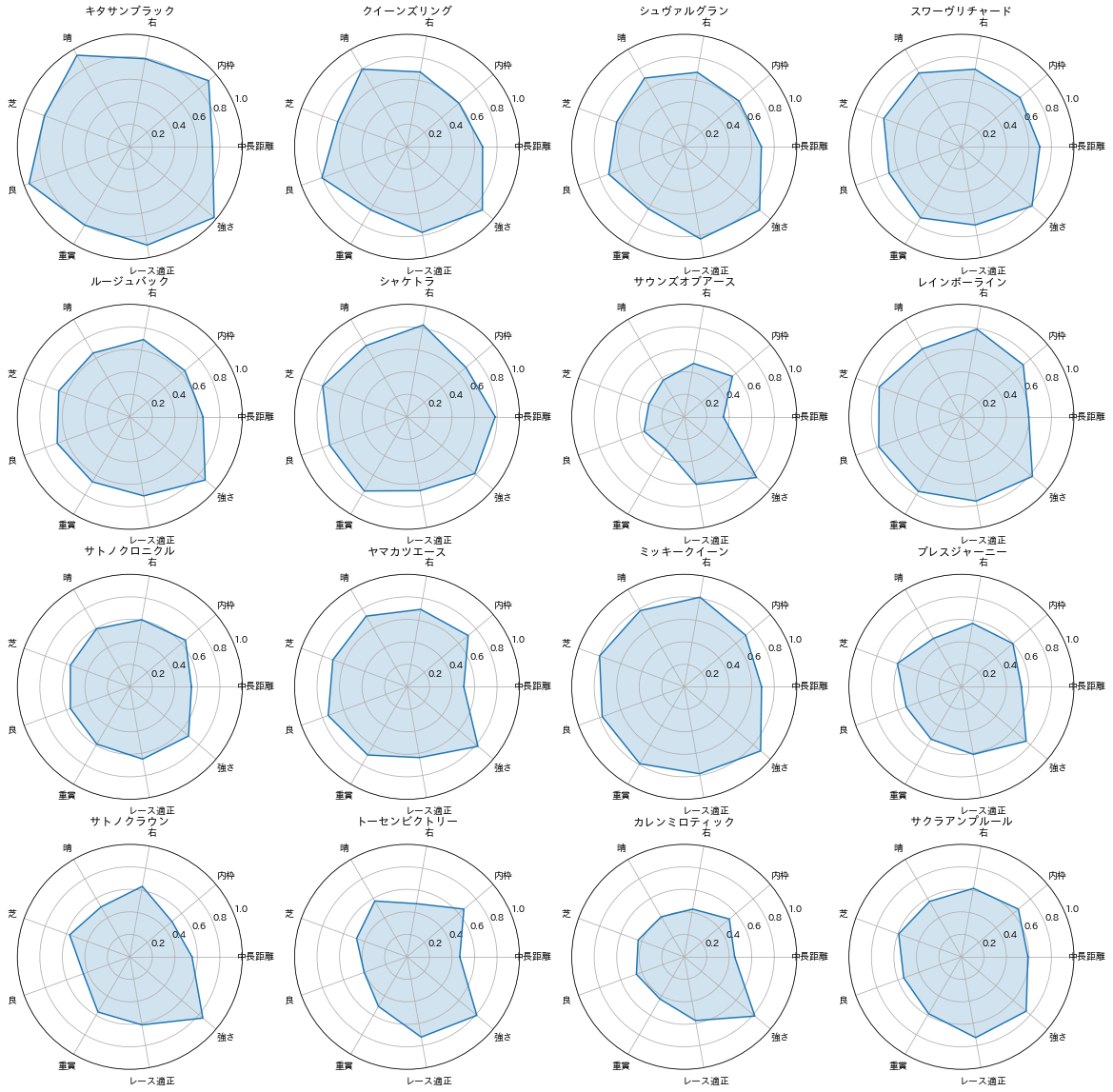
レーダーチャートを使うと、ちゃんと分析してる感があって、個人的には好きですｗ

2. 機械学習に挑戦する

次はいよいよ機械学習に挑戦します。
まだまだ、データ分析もデータクレンジングも不十分なため、十分な精度は出ないと思いますが、とりあえず現状を知る意味でもやってみます。

機械学習で予測する値ですが、着順を正確に予測するのは非常に困難かつ、不必要です。
馬券に絡むものだけ予測できれば良いことを考えると、1~3着までの馬が予測できれば十分です。
そのため、今回は以下の3クラスの分類問題として正解データを作成します。

• クラス2 : 着順が上位30%までのデータ
• クラス1 : 着順が上位70%までのデータ
• クラス0 : 上記以外

馬券に関係ないクラス1とクラス2を分離した理由としては、各クラス内のデータ数をなるべく均等にしたかったからです。
クラス数に偏りがあると、機械学習の精度が下がるのでその対策です。

2.1. 特徴量エンジニアリング

では、特徴量を作成していきます。
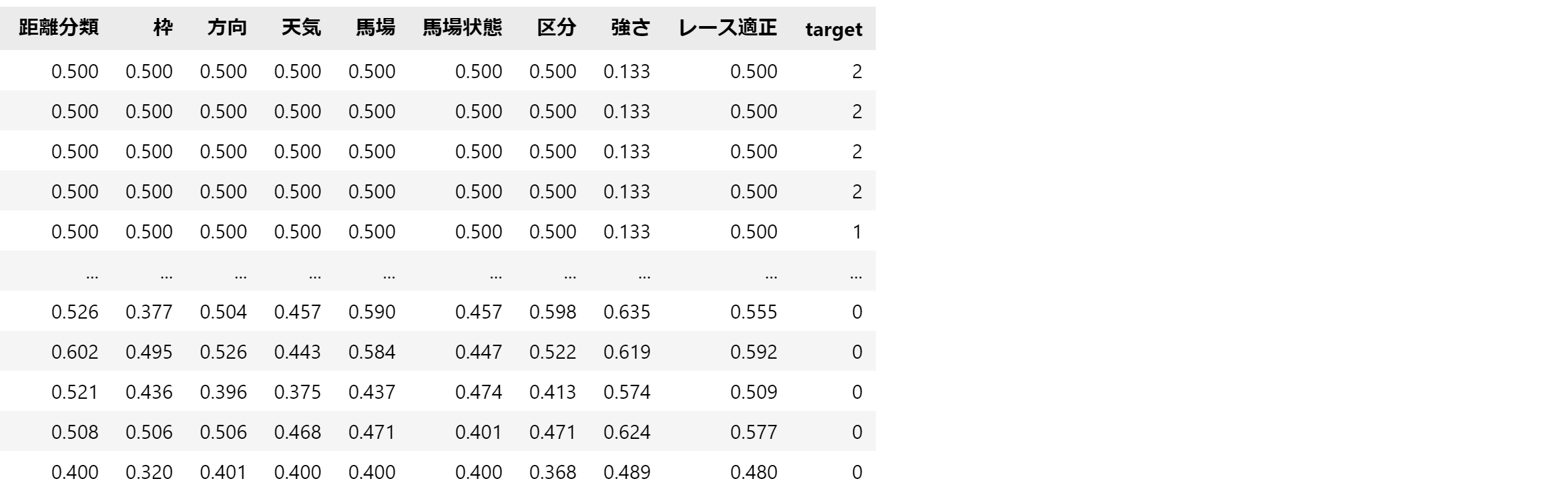
その説明をするために、まずはデータを確認してみます。

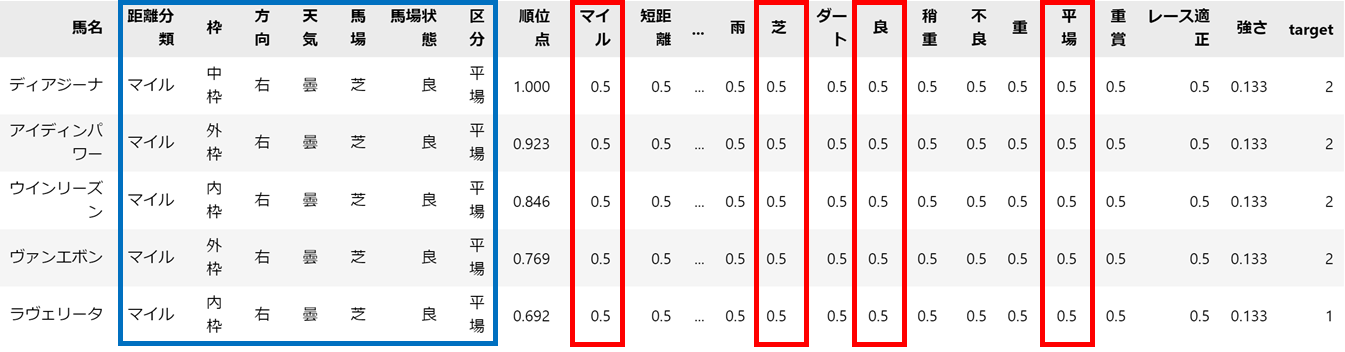
青枠に書かれているのが、今回のレースの条件です。
この条件に合致する適正がレースの予想に必要なため、必要な指標は図の赤枠部分だけになります。
まずは、この部分を抜き出しました。

columns = ['距離分類', '枠', '方向', '天気', '馬場', '馬場状態', '区分']
data_list = [[0.0 for _ in range(len(columns))] for _ in range(data.shape[0])]

for i in range(data.shape[0]):
    for j in range(len(columns)):
        data_list[i][j] = data.loc[i,data.loc[i, columns[j]]]
X = pd.DataFrame(data_list, columns=columns)
X = pd.concat([X, data[['強さ', 'レース適正', 'target']]], axis=1)

抜き出し後の特徴量は以下の通りです。

2.2. 事前データ分析

機械学習を実行する前に、各種指標と正解ラベルの関係性を見てみます。
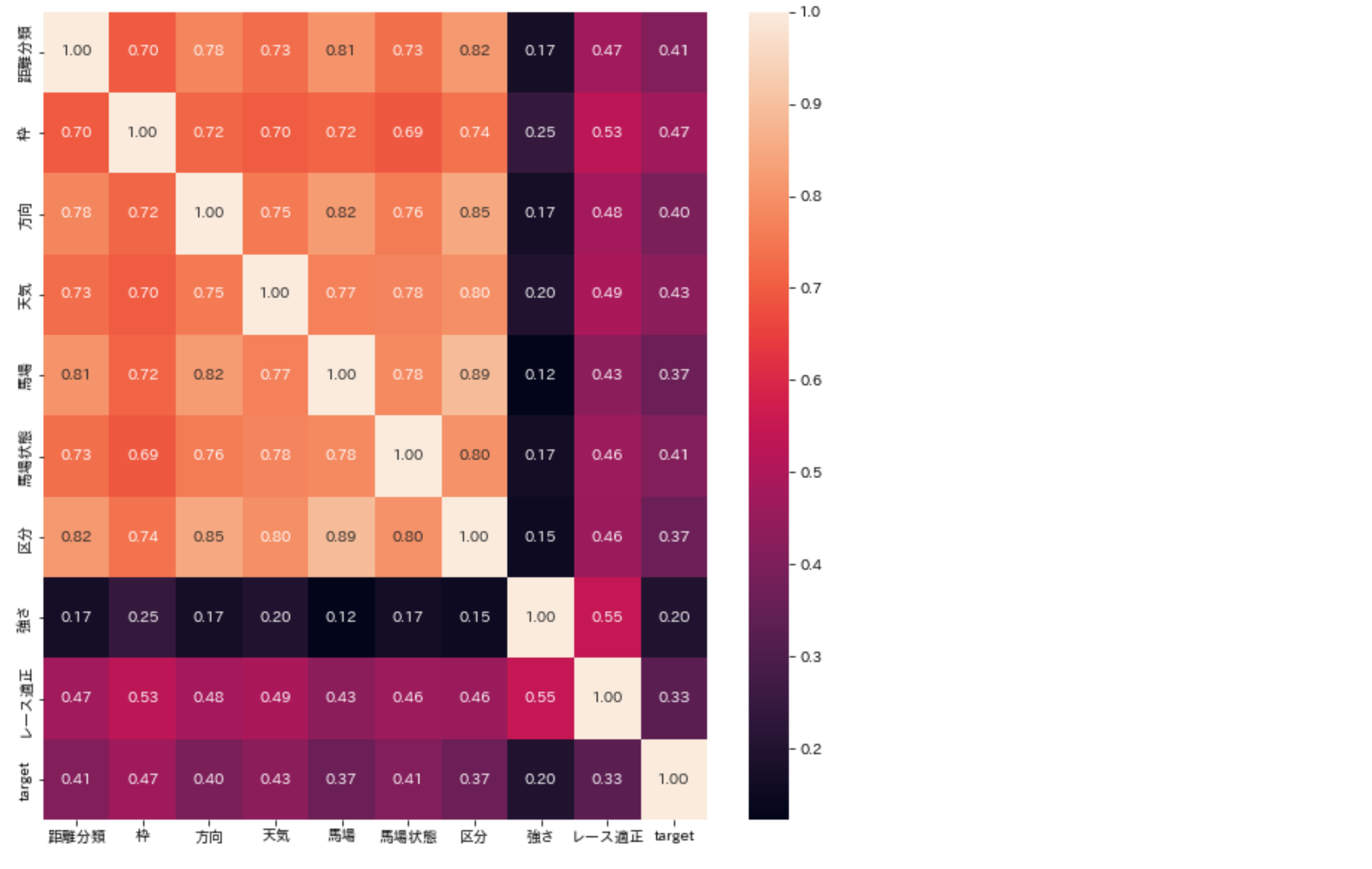
まずは、相関係数を確認します。

import matplotlib.pyplot as plt
plt.figure(figsize=(20,20))
sns.heatmap(X.corr(), annot=True, fmt='.2f')
plt.show()

正解ラベル(target)との相関が4割を超えるものもいくつかあり、それなりに期待できそうです。

次に、各特長量どうしの関係をpairplotを使った散布図で確認します。
正解ラベル(target)の値で色分けしています。
※実行に、30分以上かかりました。。。皆さんは列を絞ってください。。

import matplotlib.pyplot as plt
plt.figure(figsize=(20,20))
sns.pairplot(data=X, hue='target', palette='deep')
plt.show()

どの散布図でも概ね正解ラベルが0の青いデータが左下に、正解ラベルが2の緑のデータが右上に集まっているのが分かります。
なんとなく、上手く予測が出来そうな気がしてきました。

2.3. 機械学習の実施と結果の確認

では、実際に機械学習を実施してみます。
対象とする競馬データは時系列データのため、未来のデータを使って学習した結果を過去のデータに適用すると、データのリークが起こってしまいます。

そのため、sklearnのTimeSeriesSplitを使い、時系列順を保ってテストデータを分割していきます。
今回は、機械学習のモデルとしてRandomForestを使って予測を行いました。

from sklearn.ensemble import RandomForestClassifier
from sklearn.model_selection import TimeSeriesSplit
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score

folds = TimeSeriesSplit(n_splits=5)
train_acc_scores_ = []
test_acc_scores_ = []
train_prc_scores_ = []
test_prc_scores_ = []
train_rcl_scores_ = []
test_rcl_scores_ = []
train_f1_scores_ = []
test_f1_scores_ = []

for i, (train_index, test_index) in enumerate(folds.split(X)):
    X_train, X_test, y_train, y_test = X.iloc[train_index,:], X.iloc[test_index,:], y.iloc[train_index], y.iloc[test_index]
    forest = RandomForestClassifier(criterion='entropy', n_estimators=50, random_state=1, n_jobs=-1, max_depth=3)
    forest.fit(X_train, y_train)
    y_train_pred = forest.predict(X_train)
    y_test_pred = forest.predict(X_test)
    train_acc_scores_.append(accuracy_score(y_true=y_train, y_pred=y_train_pred))
    test_acc_scores_.append(accuracy_score(y_true=y_test, y_pred=y_test_pred))
    train_prc_scores_.append(precision_score(y_true=y_train, y_pred=y_train_pred, average='macro'))
    test_prc_scores_.append(precision_score(y_true=y_test, y_pred=y_test_pred, average='macro'))
    train_rcl_scores_.append(recall_score(y_true=y_train, y_pred=y_train_pred, average='macro'))
    test_rcl_scores_.append(recall_score(y_true=y_test, y_pred=y_test_pred, average='macro'))
    train_f1_scores_.append(f1_score(y_true=y_train, y_pred=y_train_pred, average='macro'))
    test_f1_scores_.append(f1_score(y_true=y_test, y_pred=y_test_pred, average='macro'))

print('Train')
print(f'acc : {train_acc_scores_}')
print(f'prc : {train_prc_scores_}')
print(f'rcl : {train_rcl_scores_}')
print(f'f1  : {train_f1_scores_}')
print('Test')
print(f'acc : {test_acc_scores_}')
print(f'prc : {test_prc_scores_}')
print(f'rcl : {test_rcl_scores_}')
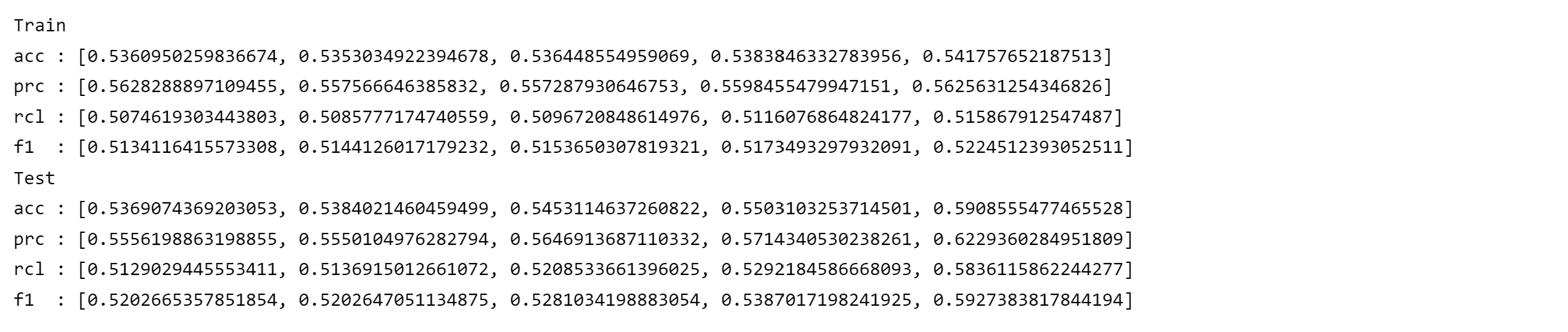
print(f'f1  : {test_f1_scores_}')

結果を確認すると、大体6割弱の正解率となりました。
また、正解率、適合率、再現率に大きな差がないことから、偽陰性や擬陽性が極端に集中しているということはなさそうです。

次に、混同行列を確認してみます。

from sklearn.metrics import confusion_matrix
confmat = confusion_matrix(y_true=y_test, y_pred=y_test_pred)
plt.figure()
sns.heatmap(confmat, annot=True, fmt='4d')
plt.xlabel('予測')
plt.ylabel('実際')
plt.show()

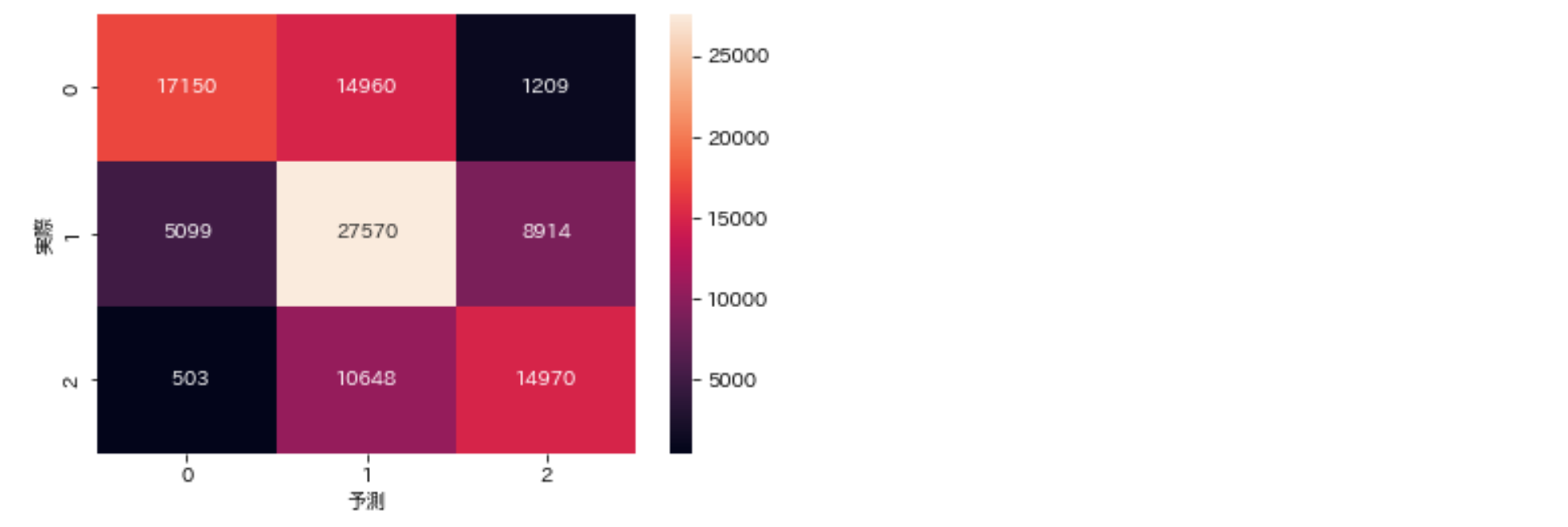
注目したいのが、表の一番右側の列です。
競馬においては、当たると予測した馬券だけを購入するため、「クラス2と予測した中での的中率」が重要になります。
この値を計算すると、$ 14970 / (14970+8914+1209) = 0.597 $となるため、やはり約6割の的中と考えてよさそうです。
一見微妙な数字ですが、ランダムに予想したときのクラス2の的中率は30%になるので、60%の的中率はそれほど悪くもなさそうです。

続いて、各特長量ごとの結果に対する寄与率を見てみます。

枠に対する適正値と天気に対する適正値の値の寄与率が高いですね。
逆に強さやレース適正の寄与率が低いのが気になります。

最後に具体的なレースの的中度合いを確認します。
こちらは、1つだけではなくいくつか紹介します。
予測列が2の値の馬が、購入する馬券に書かれると思って見てください。

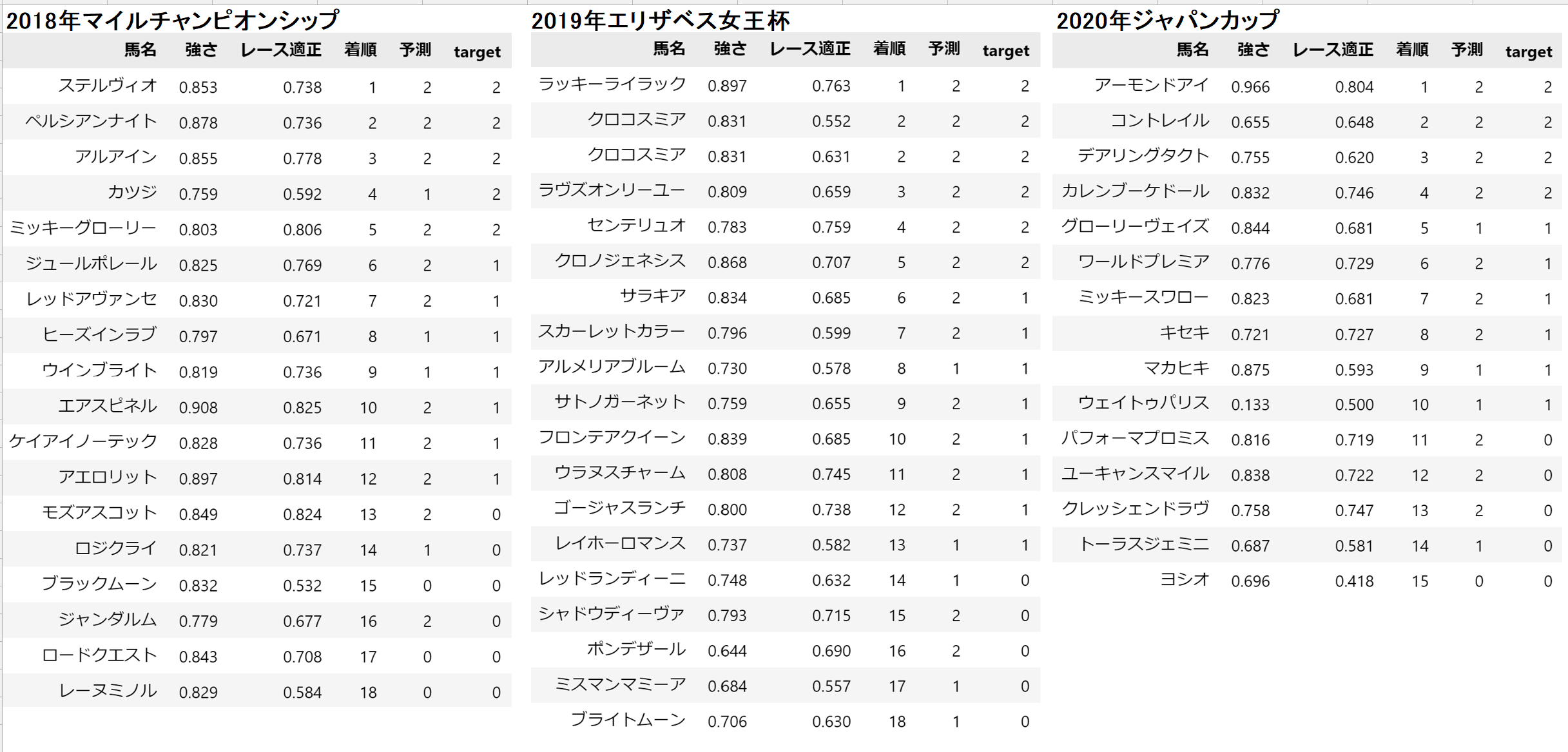
3つの例ではいずれも3着以内を当てていますが、それ以外にも無駄な馬券を買いすぎています。
回収率を上げるには、この点の改善が必須ですね。

3. 馬どうしの類似度を計算する

最後に、少し毛色の違う実験をしてみたので紹介します。
以下のテーブルには、各競走馬の最後の出走時のレース適正が格納されています。
※前回のレース適正の数値化の最後に紹介したdata_horseというテーブルの中身です。

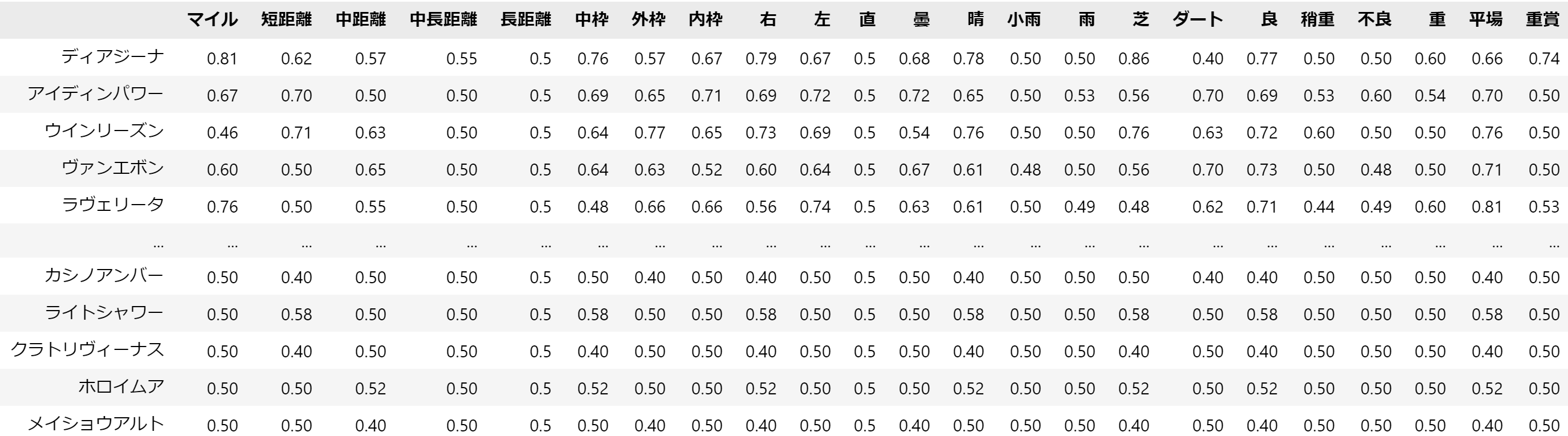
このデータに対して、協調フィルタリングを適用して、馬の適正の類似度を測ってみました。
実行したのは、以下のソースコードです。

from sklearn.neighbors import NearestNeighbors
knn = NearestNeighbors(n_neighbors=10,algorithm= 'brute', metric= 'cosine')
model_knn = knn.fit(data_horse)

horse_name = 'オルフェーヴル'
distances, indices = model_knn.kneighbors(data_horse.iloc[data_horse.index== horse_name].values.reshape(1,-1),n_neighbors=21)
for dist, idx in zip(distances[0], indices[0]):
    print(data_horse.index[idx], dist)

この手法では、data_horseの各行データを1つのベクトルとして見なします。
そして、horse_nameで指定されたベクトルとその他の馬のベクトルの類似度(コサイン類似度)を計算し、近い順にn件出力しています。

では、この結果を確認してみます。

この結果が何に役立つか分かりませんが、例えば一度も走ったことのない条件のレースの予測をする際に、この類似の馬の成績を参考にするなどに使えるかもしれません。
正直、面白そうだなと思ってやっただけなので、この後のことは何も考えてません。。。

4. まとめ

今回の数値化やその後の実験を通して、色々な分析手法を調べたりしたので、だいぶ機械学習の理解が増したと思います。
今後は、競馬データでの機械学習の精度を高めて、実際に馬券を購入していきたいと思います。
（そのためには、最新のデータまでスクレイピングをする必要がありますが、、、）

また、何か進展があったら、こちらに投稿したいと思いますのでよろしくお願いします！