元論文
MaX-DeepLab: End-to-End Panoptic Segmentation with Mask Transformers
CVPR 2021。著者はJohns Hopkins大学とGoogle Research。
面白かったのでメモ。
Max-DeepLabのポイント
Semantic SegmentationとInstance Segmentationを同時に行うPanoptic Segmentationの新しいアプローチ。1つのインスタンスが1つの出力チャンネルに対応するようにセグメンテーションすることによって、これまで困難だった複雑な形状の物体や近接した物体のセグメンテーション精度を高めている。
下図は、従来手法であるAxial-DeepLabやDetectoRSでセグメンテーションできなかったチェアを、MaX-DeepLabで正しくセグメンテーションできている例。Axial-DeepLabは各画素ごとに物体の中心位置を予測し、中心位置の近い画素を同じインスタンスに割り当てるため、犬とチェアが同じインスタンスとしてセグメンテーションされている。DetectoRSは検出矩形ごとにSemantic Segmentationを行うため、チェアの検出矩形(茶色矩形)に対するチェアの尤度が低く、正しく分類できていない。MaX-DeepLabはこれら既存手法の限界を原理的に解消した手法である。

Panoptic Segmentationとは
Panoptic SegmentationはSemantic SegmentationとInstance Segmentationを同時に行う難易度の高いタスクである。すなわち、Instance Segmentationのように人や車など同じクラスの異なる物体を区別しつつ、空やビルといったのセグメンテーションも行う。ただし、ビルや木といった背景に登場することの多いクラスは個々の物体を区別しなくてよい(Instance Segmentationしなくてよい)。人や車のように個々の物体を区別しなくてはならないクラスをThingクラス、空やビルなど個々の物体を区別しなくてよいクラスをStuffクラスと呼ぶ。例えばCOCOデータセットでは全133クラスのうち、Thingクラスは80クラス、Stuffクラスは53クラスとなっている。
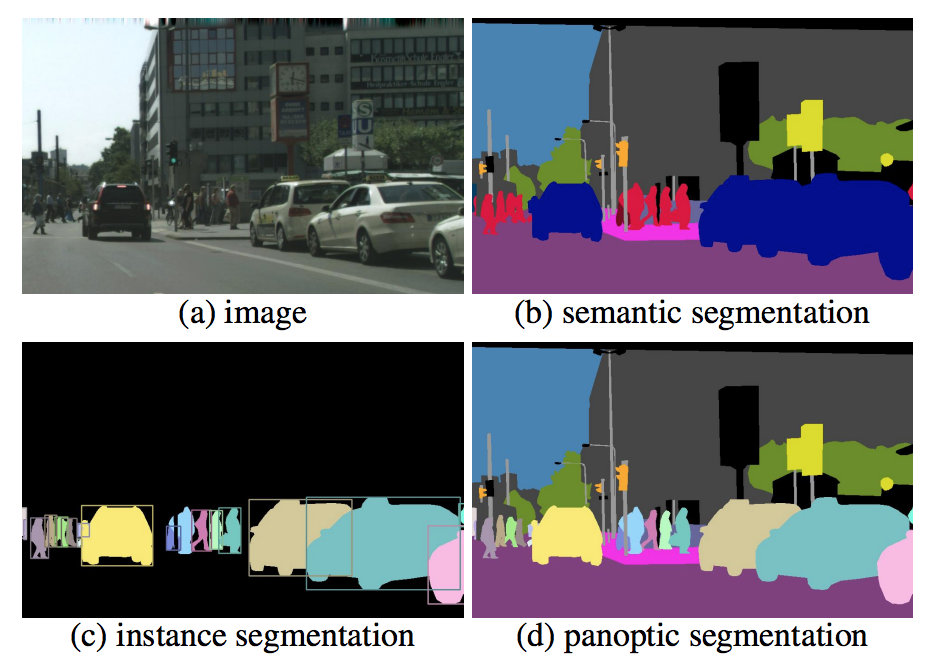
([1]より引用)
推論
MaX-DeepLabの推論時の挙動。
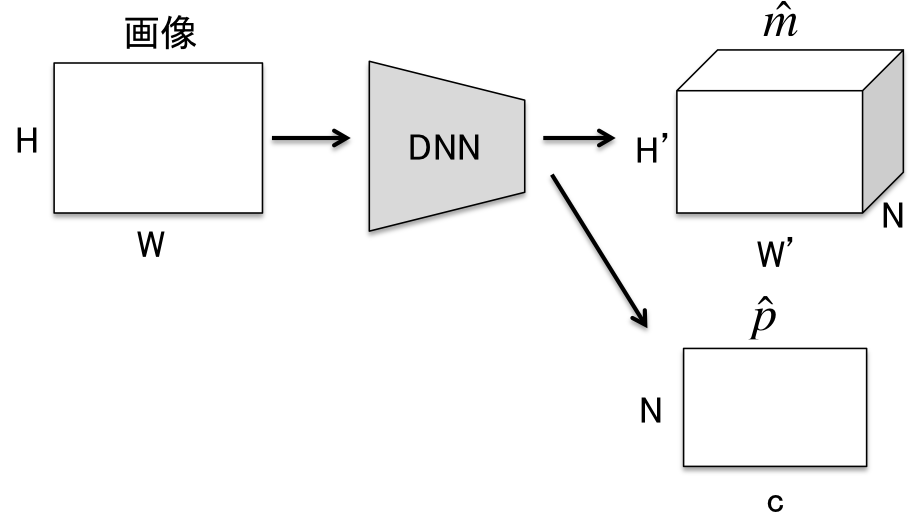
DNNの入力は高さ$H$、幅$W$の画像。出力は$H' \times W' \times N$のマスク$\hat{m}$と$N$個分のカテゴリカル分布$\hat{p}$。$H'$、$W'$は計算量削減のため$H$や$W$より小さい値になるよう設定される。論文では$H'=H/4$、$W'=W/4$。$N$は予め設定されるハイパパラメータで、画像1枚に出現するインスタンス数よりも十分大きい数とする。論文では$N=128$。MaX-DeepLabではこの$N$が重要な役割を果たす。
$\hat{m}$の各画素に対応する$N$次元ベクトルは総和1の確率値になるよう正規化されている($\sum_{i=1}^{N}\hat{m}_i=1^{H' \times W'}$)。$\hat{m}$はチャンネルごとに異なるインスタンスのマップを予測するよう学習されている。しかし、$\hat{m}$だけではどのマップがどのクラスに対応するかはわからない。そこで、クラス確率$\hat{p}$を用いる。クラス確率$\hat{p}$は$\hat{p}_i$がマップ$\hat{m}_i$のクラスを予測するように学習されている($i=1,2,\dots,N$)。ただし、予測されるクラスには物体なしクラス$\varnothing$を含む。
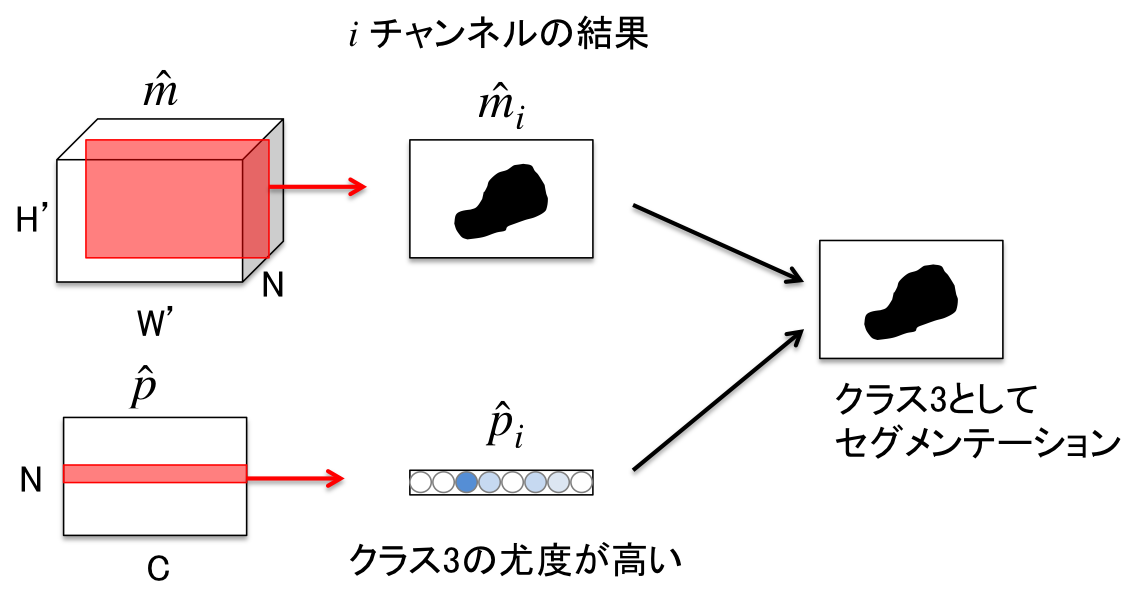
マスク$\hat{m}$とクラス確率$\hat{p}$から最終的なセグメンテーション結果を算出する方法は非常にシンプル。下図のようにチャンネルごとにマップと最尤クラスを割り当てればよい。
入力画像に含まれるインスタンスが$N$個以下の場合、余分なチャンネルのマップのすべての値を0とするか、$\varnothing$のクラス確率が高くなるように予測すればよい。
入力画像に含まれるインスタンスが$N$より多い場合、MaX-DeepLabでは原理上正しくセグメンテーションすることができない。これがMaX-DeepLabの最大の制約である。
学習
推論で述べた入出力を実現するDNNの学習方法。
損失の設計
メインのPQ-style lossと、補助的な3つの損失の和で構成される。
式の定義
準備として式の定義を整理。
正解データ$y$は以下の式で与えられる。
\{y_i\}^K_{i=1} = \{(m_i, c_i)\}^K_{i=1}
$K$は画像に含まれるインスタンスの数であり、$m_i$、$c_i$は$i$番目のインスタンスのマスクとクラスを表す。マスクは0か1で表され、重複はないものとする。
予測結果$\hat{y}$は以下のように書く。前述の通り$\hat{m}_i$は$i$チャンネル目のマスク、$\hat{p}_i(c)$は$i$チャンネル目のクラス$c$の確率を表す。
\{\hat{y}_i\}^N_{i=1} = \{(\hat{m}_i, \hat{p}_i(c)\}^N_{i=1}
PQ-style loss
panoptic segmentationではrecognition quality(RQ)とsegmentation quality(SQ)をかけ合わせたpanoptic quality(PQ)という評価指標が用いられる。
\rm{PQ}=\rm{RQ}\times\rm{SQ}
このPQをそのまま損失にしたものがPQ-style lossとなる。
まず、$i$番目のインスタンスの正解$y_i=(m_i,c_i)$と$j$チャンネル目の正解$\hat{y}_j=(\hat{m}_j,\hat{p}_j(c))$の類似度${sim}(y_i,\hat{y}_j)$は以下の式で表される。
{sim}(y_i,\hat{y}_j)=\hat{p}_j(c_i) \times {Dice}(m_i,\hat{m}_j)
ここで、右辺の前半部分$\hat{p}_j(c_i)$はクラス確率の予測の一致度、すなわちRQを表し、後半部分はマスクの予測の一致度、すなわちSQを表す。なお、$Dice(m_i,\hat{m}_j)$は$m_i$と$\hat{m}_j$が等しいときに最小となり、異なるほど大きい値を取るようなDice損失と呼ばれる損失項である。
このように$y_i$と$\hat{y}_j$の類似度の計算は比較的単純である。
問題は、どの$y_i$と$\hat{y}_j$をペアとして類似度を取ればよいかである。例えば、$K$個の正解$y_1,\dots,y_K$と$N$個の予測$\hat{y}_1,\dots,\hat{y}_N$のすべての組み合わせの類似度の総和を損失として設定するとどうなるか。この場合、$\hat{y}_1,\dots,\hat{y}_N$が正解と一致するような理想的な値のときに、必ずしも損失が最小値を取らない。そのような損失を最小化するようDNNを学習した場合、おそらく$K$個の正解マスクやクラスを平均したような$N$個の出力が得られると考えられる。
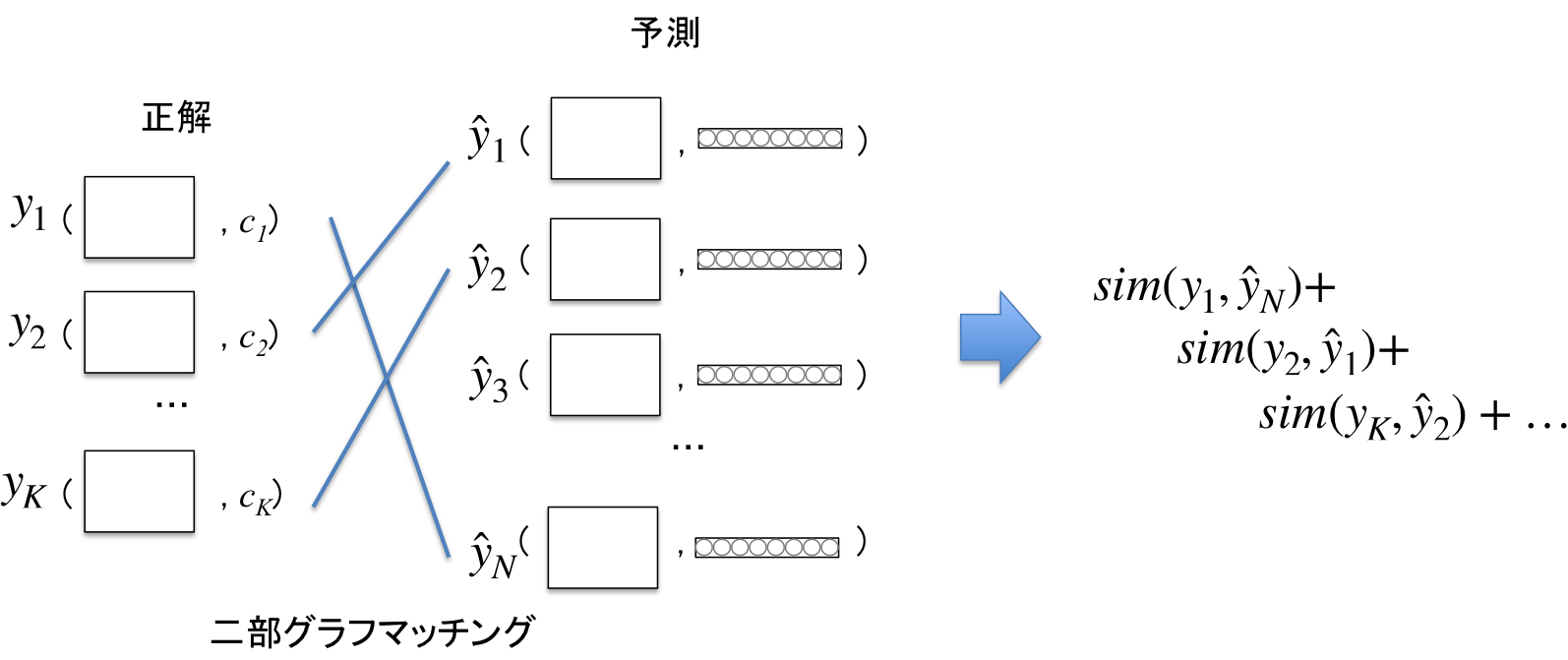
MaX-DeepLabでは、一旦すべての組み合わせで類似度${sim}(y_i,\hat{y}_j)$を計算した後、重複なく最も類似度が高くなるペアをマッチングし、マッチしたペアの類似度の総和を損失とする。こうすることで、損失を最小化した際に理想的な$\hat{m}$、$\hat{p}$が得られるようになる。
類似度の合計が最大となる$y_i$と$\hat{y}_j$のマッチングは、競技プログラミングでおなじみの二部グラフの最小重み最大マッチング問題で、Hungarianアルゴリズムを用いて解くことができる。実装する際はscipy.optimize.linear_sum_assignment
などのライブラリが利用可能。
ペアにならなかった$\hat{y}_j$(上図では$\hat{y}_3$)は$\varnothing$の確率が高くなるようクロスエントロピー損失を与える。
この損失は既存手法には見られないアプローチで、よくできているという印象。
なお、実際には効率的なDNN最適化のため、より複雑な類似度の計算式を用いているが、本記事では省略。
instance discrimination loss
インスタンスごとに異なる特徴表現が獲得されるようにするための補助損失。
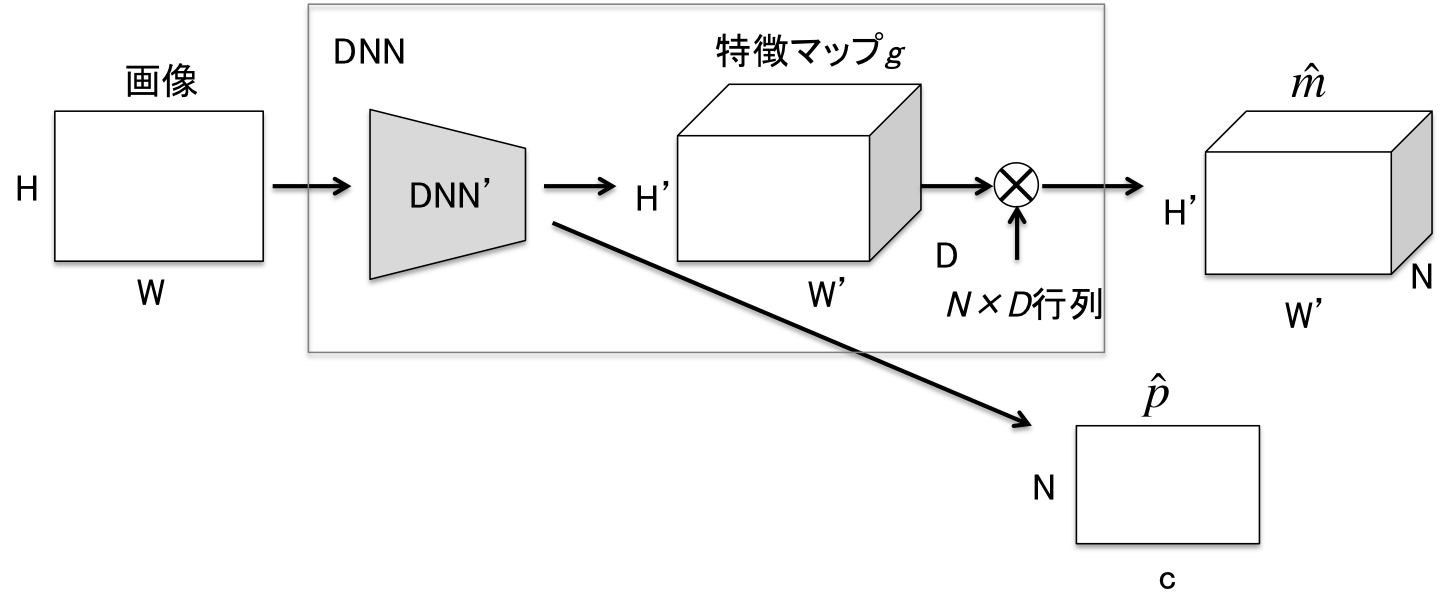
MaX-DeepLabでは出力直前の$H'\times W' \times D$の特徴マップ$g$に$N\times D$の行列(後述)をかけてマスク$\hat{m}$を得る。
$g$はピクセルごとの$D$次元の特徴ベクトルとみなすことができる。
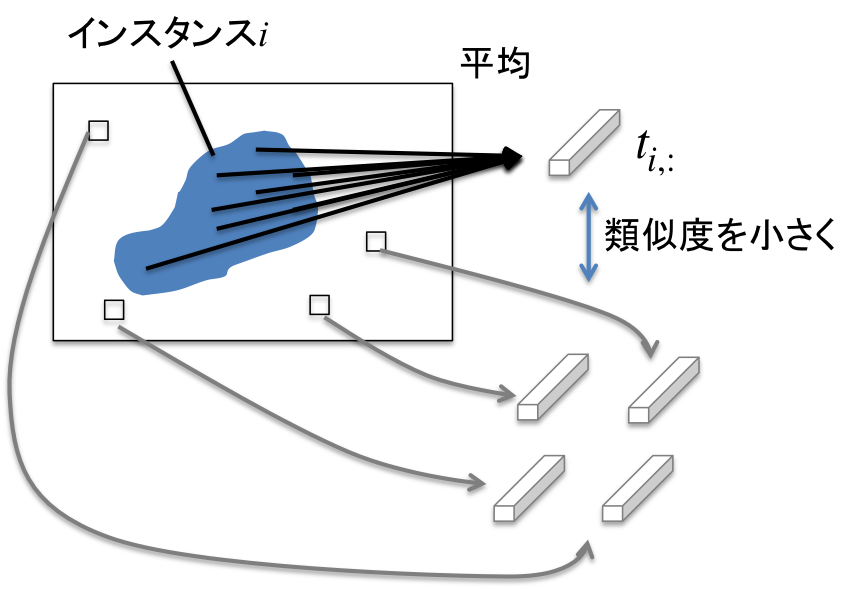
今、$g$を正解マスク$m_1,\dots,m_K$でフィルタした平均ベクトル$t_{1,:},\dots,t_{K,:}\in \mathbb{R}^D$を考える。
t_{i,:}=\frac{\sum_{h,w}m_{i,h,w}\cdot g_{:,h,w}}{||\sum_{h,w}m_{i,h,w}\cdot g_{:,h,w}||}
$g_{:,h,w}$はピクセル$(h,w)$に対応する$D$次元特徴ベクトルである。直感的には$t_{i,:}$はインスタンスごとの平均特徴ベクトルとみなすことができる。
instance discrimination lossは$t_{i,:}$を用いて以下の式で表される。
\mathcal{L}^{InstDis}_{h,w} = -\log \frac{\sum^K_{i=1} m_{i,h,w}exp(t_{i,:}\cdot g_{:,h,w}/\tau)}{\sum^K_{i=1}exp(t_{i,:}\cdot g_{:,h,w}/\tau)}
$\tau$は温度パラメータである。
$\mathcal{L}^{InstDis}$は、ある正解インスタンスのマスク$m_i$に対し$m_i=1$となるピクセルの平均特徴ベクトルが、$m_i=0$となる全てのピクセルの特徴ベクトルと類似度(論文ではコサイン類似度)が小さいほど小さい値を取る。
以上のように、instance discrimination lossによって同じインスタンスに属さないピクセルの特徴ベクトルは類似度が低くなるように学習される。結果的にインスタンスごとに異なる特徴が学習され、インスタンスセグメンテーションの精度を向上させることができると考えられる。
Mask-ID cross-entropy loss
$N$個のマスクについて、二部グラフマッチングの対応結果に基づいてクロスエントロピー損失を与える。すなわち、ピクセル$(h,w)$に対し、対応付けられた正解マスクの$(h,w)$の値が1となるチャンネルを1、それ以外を0とするようクロスエントロピーを計算する。
semantic segmentation loss
instance discrimination lossでは同じクラスの異なるインスタンスと、異なるクラスの異なるインスタンスが同等に扱われている。出力層から適度に離れた中間層の特徴表現から、semantic segmentaionを行うブランチネットワークを学習することで、異なるインスタンスでも同じクラスであれば比較的近い特徴表現が学習され、RQ向上に寄与すると考えられる。
semantic segmentationが効きすぎると同じクラスで異なるインスタンスの区別に悪影響を与えると考えられるため、絶妙なバランス係数の調整が必要。
ネットワーク構成
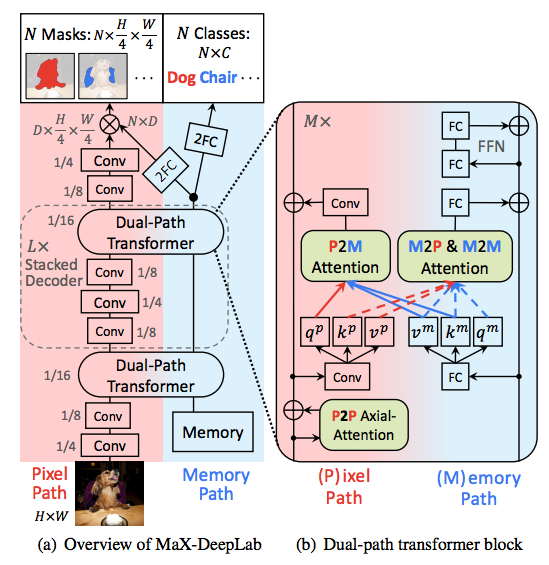
MaX-DeepLabではMask Transformerと呼ばれるネットワーク構造を提案している。
通常のTransformerを用いた画像系タスクで見られるPixel pathに加えてMemory pathを持つDual Path構造が特徴的。Memory pathの入力は学習可能なmemory feature $x^m\in \mathbb{R}^{N\times d_{in}}$であり、$N$個の$d_{in}$次元のmemory featureが出力の各チャンネルに対応した情報を保持するように学習されることが期待されている。Pixel pathとMemory Pathは、Attention機構によって相互に作用し合い、層が進むにつれてPixel pathはインスタンスの形の情報、Memory pathはインスタンスのクラスの情報を抽出するように学習されるものと考えられる。
前述通り、MaX-DeepLabでは特徴マップ$g\in \mathbb{R}^{H'\times W'\times D}$から$\hat{m}\in \mathbb{R}^{H'\times W'\times N}$を計算するために$N\times D$行列を用いるが、この行列はMemory pathから計算される。この$N\times D$行列は、どのような$D$次元特徴ベクトルが出力マスクのどのチャンネルで活性化するかを表している。
実験結果
定量評価
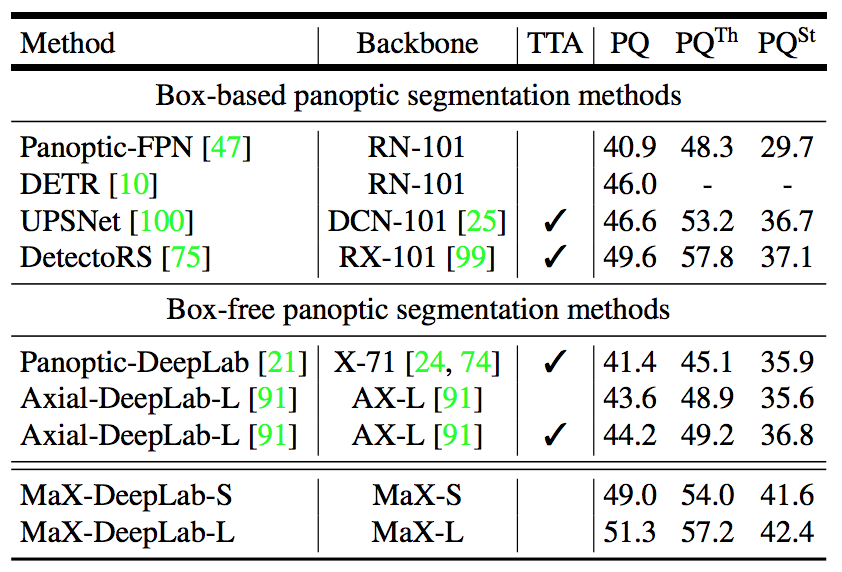
COCOデータセットでの実験結果は以下の通り。既存手法最良のDetectoRSを上回っている。著者曰く、box-based手法を超えたbox-free手法は初とのこと。特に他手法と比較してStuffクラスで大幅な精度向上が見られる点が特徴的である。これに対する考察は後述する。
定性評価
セグメンテーション結果例。左から入力画像、MaX-DeepLab(提案手法)、Axial-DeepLab、DetectoRS、DETR、正解。
Box-basedのDetectoRS及びDETRでは、子供と大人のBounding Boxが近いために一つのインスタンスとしてセグメンテーションしてしまっているが、MaX-DeepLabではきれいにセグメンテーションできている。その他にも素晴らしいセグメンテーション結果例が載っているが本記事では省略。
下図は失敗例。左から入力画像、MaX-DeepLab(提案手法)、Axial-DeepLab、DetectoRS、DETR、正解。
集合写真のようにインスタンス数が多い画像は苦手。(この例では正解のアノテーションが不正確だが、それぞれの人とネクタイがインスタンスとしてセグメンテーションされる動作が理想的)
詳細分析
以下、内部的な挙動についての分析。
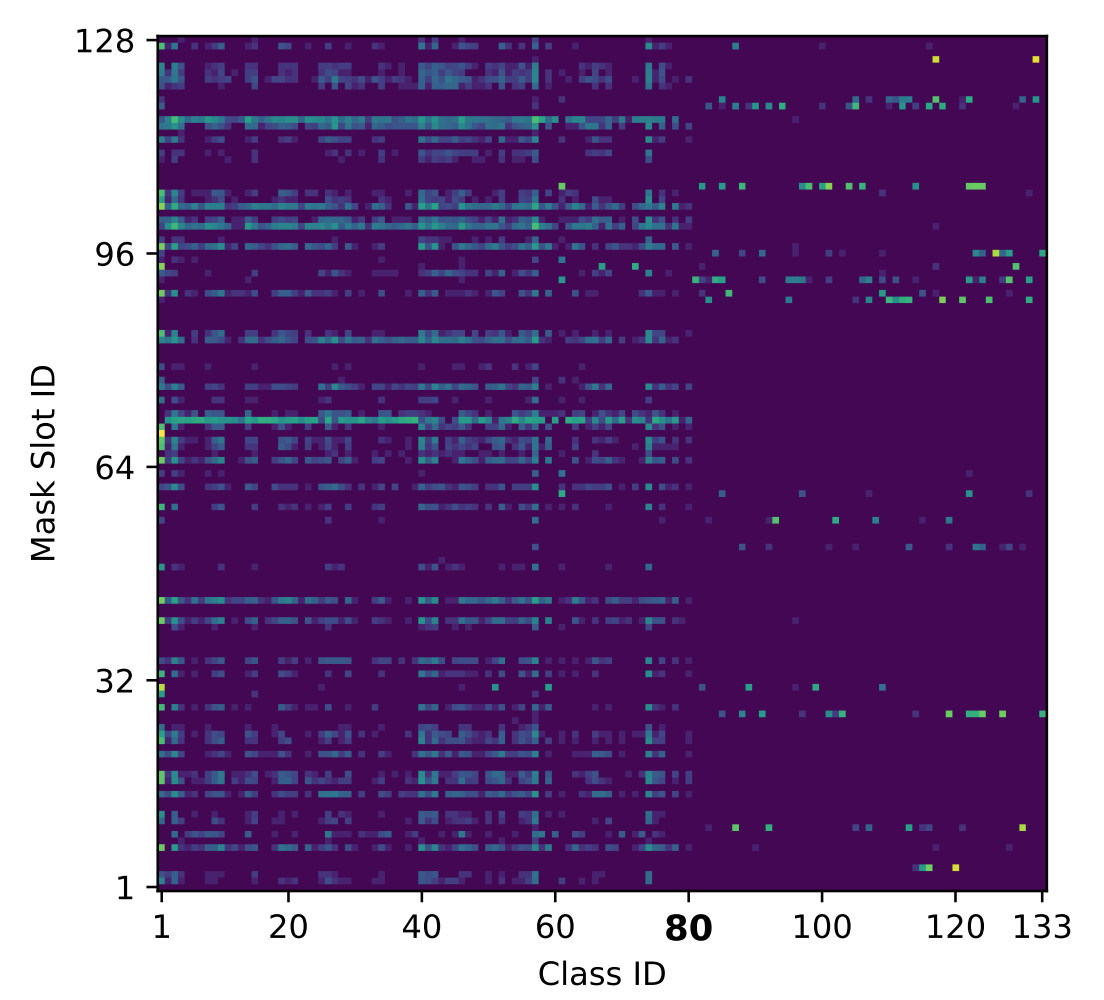
下図は$N=128$、クラス数133(Thingクラス80、Stuffクラス53)のとき、出力のどのチャンネルがどのクラスに発火しやすいかを表している。
まず、横軸の80を境に左右で模様が大きく異なり、Thingクラスに発火しやすいチャンネルとStuffクラスに発火しやすいチャンネルが異なることがわかる。更に詳しく見るために、最も高頻度で発火する上位8チャンネルの平均マスクを示したのが下図である。
最も発火したのは71チャンネル目でほぼすべてのThingクラスで発火していた。Class IDとMask Slot IDのマトリックスの図を見ても、縦軸71のあたりで黄色の線を確認できる。この平均マスクは、「Thingクラスは画像中心に来ることが多い」ということを示している。次に発火頻度の高い106チャンネル目は、道、床、ダイニングテーブルといったStuffクラスに発火することが多かった。平均マスクも画像下部が明るくなっており、納得である。125チャンネル目で発火したクラスの99.9%は壁と木であった。69チャンネル目は完全に人クラスのみで発火していた。
以上のように、MaX-DeepLabでは空間的領域とクラスをセットととして、チャンネルごとに役割分担しながら学習がなされているものと考えられる。
下図は特徴マップ$g$がインスタンスごとに異なる特徴ベクトルを獲得できているかを可視化した図である。
上図左は入力画像、右はセグメンテーション結果であるが、中央列は$D=3$で学習したMaX-DeepLabの特徴マップ$g$を画像として可視化したものである点に注意が必要である。すなわち、異なる色は特徴空間上で離れたベクトルを、似た色は近いベクトルを表している。図を見ると、インスタンスごとに異なる色で塗られており、同じクラスであってもインスタンスごとに異なる特徴を獲得できてることがわかる。
個人的には象の右の木の幹と背景の木々で若干色が異なっている点が驚異的と感じた。Panoptic Segmentationとしては木はStuffクラスなのでインスタンスを区別する必要はないが、MaX-DeepLabは内部的に木クラスもインスタンスを区別し、最終層の計算でマージしているものと考えることができる。そのように狙って手法やアノテーションを設計したわけではなく、自動的にそのようなDNNが獲得された点がさらに面白い。このような挙動は既存手法では難しく、End to endかつシンプルな手法でPanoptic Quarityが高くなるよう最適化されたMaX-DeepLabの筋の良さが伺える。これは、MaX-DeepLabが高精度にStuffクラスをセグメンテーションできる一因と考えられる。
推論速度
小さい方のアーキテクチャMaX-DeepLab-Sの推論速度は既存手法と同等で、1枚あたり131ms @ V100 GPU。SoTAを出したMaX-DeepLab-Lの推論速度は記載されていない。