はじめに
今回はテキストの差分検出などで使われる Wu らによる O(NP) のアルゴリズムの解説をしつつ、後半ではGoで実装していこうと思います。
ざっくり書いてみたら量がめちゃめちゃ多かったので、いくつかに分けて投稿しました。
の3部に分かれています。
元論文は An O(NP) Sequence Comparison Algorithm by described by Sun Wu, Udi Manber and Gene Myers です。気になる方はそちらもどうぞ。
最終的な実装を確認したい方は https://github.com/convto/onp に置いてあるのでそちらをごらんください。
これは Makuake Development Team Advent Calendar 2019 - Adventar の4日目の投稿です(めちゃめちゃ遅刻しました)
テキストの差分検出とは
たとえばdiffや差分と聞いてパっとイメージが湧くのは diff コマンドのような+-のdiffが出力されるようなプログラムだと思います。
$ diff -u a.txt b.txt
--- a.txt 2019-12-05 01:02:26.000000000 +0900
+++ b.txt 2019-12-05 01:02:41.000000000 +0900
@@ -1,4 +1,6 @@
a
-b
c
+b
d
+e
+f
このような、入力Aと入力Bの間を埋めるような挿入、削除の最短手順のことを SES(Shortest Edit Script) といいます。言葉まんまでわかりやすいですね。
また、入力Aと入力Bがどれくらい異なっているか数値化したものを 編集距離(Edit Distance) といいます。
だいたいSESの挿入と削除の回数を合計したものが編集距離として扱われていると思います。
編集距離をSESの挿入と削除の回数の合計とすると、先程のdiffコマンドの例の編集距離は 挿入x3 + 削除x1 で4です。
入力Aと入力Bの最長の共通部分列を LCS(Longest Common Subsequence) といいます。これもまんまですね。
同じく先程のdiffの例でいうと、LCSは acd です。
差分の検出とは、入力Aと入力Bを比較して、
- SES
- 編集距離
- LCS
を取得し、任意の形で利用する処理である、ということができると思います。
エディットグラフとは
差分検出のアルゴリズムの説明をするにあたって、エディットグラフというものがよくつかわれるので、それについて説明します。
文字列の差分を計算するということは、入力Aと入力Bをそれぞれ比較し、それぞれの文字列について互いに一致しているか確認し、一致していなければ挿入もしくは削除を行い、最終的に入力Aと入力Bが同じ文字列になるまでの組み合わせの中で編集距離が最も短いもの(または実用に足るレベルの十分に短いもの)を選ぶ、ということです。
それぞれA,Bの文字列をグラフとみたてて、挿入をy方向の移動、削除をx方向の移動、要素が同一な場合はx,yの対角線方向に移動します。

X軸またはY軸に +1 するのをコスト1、x軸とy軸の対角線上に +1 するのをコストなしとします。
このような図のことをエディットグラフといいます。
エディットグラフを利用すると、最短編集手順を求める問題を 点(0,0) と 点(M,N) を通るいくつかの編集手順のうち、最も短いもの(SES)をもとめること、と言い換えることができます。
探索経路をグラフで表現することで削除や挿入の操作をx,y軸への移動として考えることができます。
Wu らによる O(NP) アルゴリズムの仕組み、考え方
差分の検出には、編集距離が最も短くなるケースの編集距離、SES、LCSを求めれば良いことがわかりました。
そもそも、差分の計算は負荷の大きい処理です。
何も考えずに総当りで実装しようとすると、計算量、メモリ使用量ともに非常に大きくなります。たとえば
入力A,入力Bに対してすべての組み合わせの編集手順を洗い出し、そのうちもっとも編集手順が短いものを選ぶ
などの実装をすると計算量は要素数が増えると指数的に増大します。
これらの問題をマシンパワーではなく知性で解決するのがアルゴリズムの面白いところです。
差分検出で使われることの多いいくつかのアルゴリズムをそれぞれ利用することで、この計算量を下回る事ができます。
今回はそのうち、 Wu らによる O(NP) アルゴリズムについて説明します。
O(NP) アルゴリズムの説明のために、まず、以下の定義をします
- 入力A,B の長さをそれぞれ
M, Nとする(このときM <= N) -
Δ = N - Mとする - 削除の合計回数を P とする
以下の例のように、デルタは取りうる編集距離の中で一番小さい値になります。
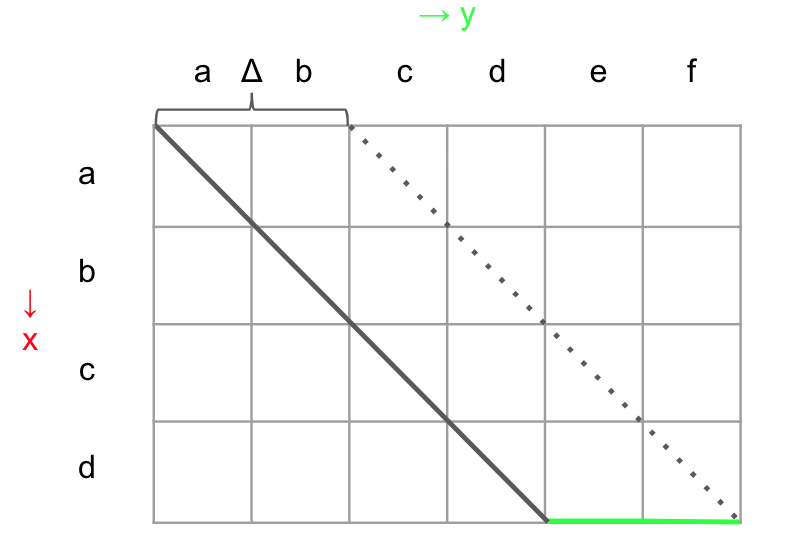
編集距離がΔと一致するケースは、比較対象がLCSと完全一致しているときです。
図
そうでない場合は Δから逸れたぶんだけ復帰する必要があります
斜めに一直線に進む線を k として k = x - y とします。
挿入方向にずれても、削除方向にずれても k = Δ となる対角線上に復帰するために対となる編集をする必要があります。
これは、 点(M,N) は必ず k = Δ となる線上に存在するためです。ずれた分は戻らないと 点(M,N) にたどり着きません。
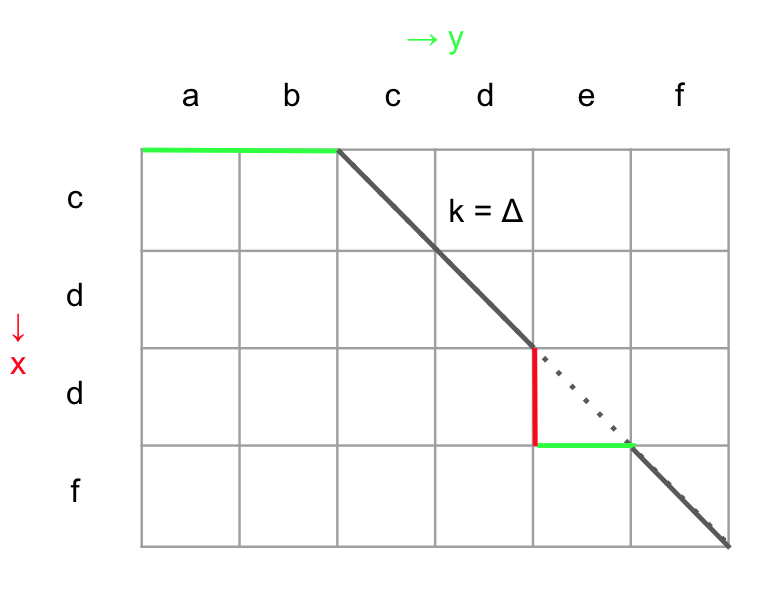
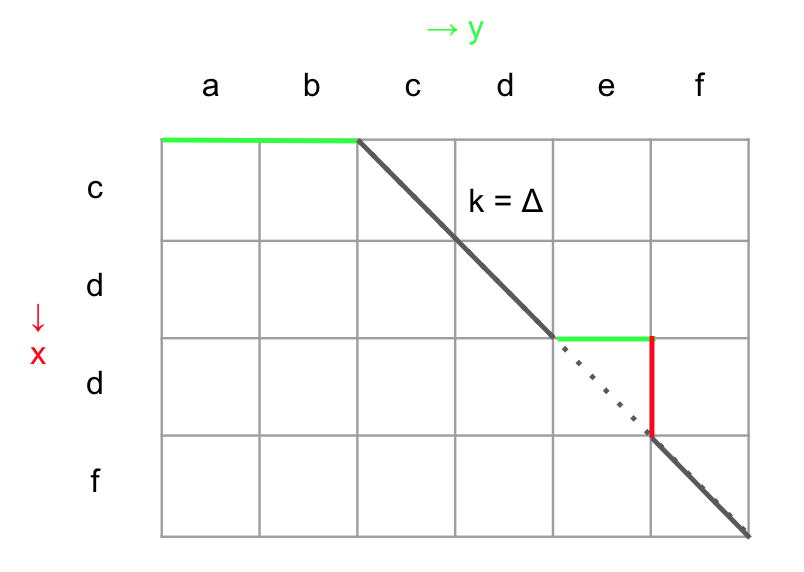
Δから逸れる、というのは Δの値より多い回数挿入される ということです。
Δより多い挿入を求めるには、P(削除回数)をかぞえればすみます。
なぜなら、Δから逸れたら、復帰するために対になる編集をする必要があるためです。
編集距離がΔと一致するケースは比較対象がLCSと完全一致するときで、そのケースに削除の手順はありません。(LCSと完全一致しているので削除の必要がない)
編集距離がΔと一致するケースからどのくらい逸れたか、というのを確認するためには、P(削除回数)を数えれば良いです。
挿入と削除は対になっているので、Δが示す比較対象がLCSと完全一致する場合の編集距離に、P * 2 をすれば編集距離が求まるので、編集距離をDとすると
D = Δ + 2P
となります。
このとき k の取りうる範囲はPによって求められ、以下の色付け範囲になります。
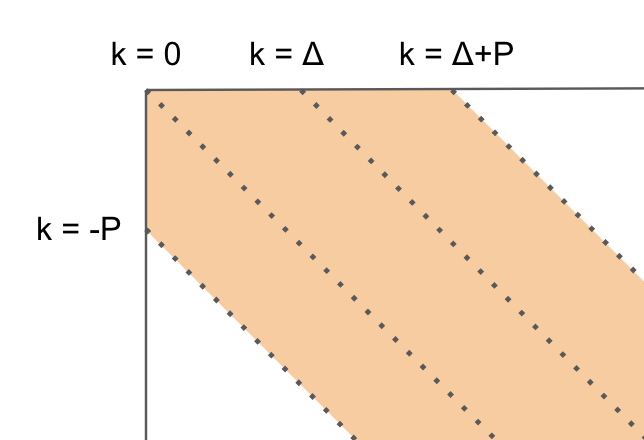
これは、この範囲を越えるとP(削除回数)より実際の削除回数が多くなってしまい矛盾するためです。
このとき k の取りうる範囲は
k ∈ [-p, Δ+p]
と表現できます。
ある削除回数Pに対してKのとりうる範囲は、総当りで探索するよりも少ないですね!
以上のように O(NP) の考え方を使うと、すべての組み合わせを探索するよりも探索対象を狭めることができます。
Pの値はわかりませんから、実際の実装では P をキーにしてループして探索していくことになります。
探索序盤で見つかればコストが低くなるのはもちろん、最悪のケースでも計算量を抑える事ができます。
今回のまとめ
- 差分検出するには
SES,編集距離,LCSを求めればよい - エディットグラフとは、削除、挿入などの手続きをグラフ化したもの。ほかの差分検出アルゴリズムの説明に用いられることもある
- 編集距離Dは
D = Δ + 2Pで求めることができる - kのとりうる範囲は
k ∈ [-p, Δ+p]
というところまで説明しました。
Wu らによる O(NP) アルゴリズムでは、k の探索範囲で示した図のように全探索などド比べて探索量が減ることがわかったと思います。
さて、探索範囲が減り計算量が小さくなる理屈はわかりましたが、これらをプログラムとして実装するには、どのように p, k について探索していくのか整理する必要があります。
次回は ②探索方法 です!ぜひこちらも読んでみてください!
参考文献
- https://www.sciencedirect.com/science/article/pii/002001909090035V 元論文
- https://gihyo.jp/dev/column/01/prog/2011/diff_sd200906 概要がすごくわかりやすかったです。仕組みの解説の部分の構成を参考にさせて頂きました。